| Дискретні динамічні системи
Завдання №1
Динаміка національного доходу Yt
визначається рівнянням
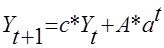 (1.1.0) (1.1.0)
де с=0,25; А =1; а=2. Знайти залежність Yt
, якщо Y0
=1
Рішення
1. Варіант початкових даних Y0
=1.
Рішення рівняння (1.1.0) проводимо в пакеті MAPLE7:
> rsolve({y(n)=1/4*y (n‑1)+1*(2^n), y(0)=1}, y(n));
>
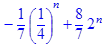
> R3:=simplify(%);
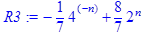
Результат:
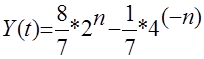
| n
|
Y
|
| 0
|
1,00
|
| 1
|
2,25
|
| 2
|
4,56
|
| 3
|
9,14
|
| 4
|
18,29
|
| 5
|
36,57
|
Завдання №2
Динаміка національного доходу Yt
визначається рівнянням Самуельсона-Хікса [6]
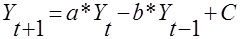 (1.2.0) (1.2.0)
де а=2; b =1,25; c=1. Знайти залежність Yt
, якщо Y0
=0, Y0
=1
Рішення:
1. Динаміка об'єктів різної природи часто описується лінійними кінцево-різницевими рівняннями виду
xt
= F
(xt‑1
, xt
-2
,…, xt-n
), (1.2.1)
Характеристичний стан об'єкта xt
у будь-який момент часу t
зі станами в попередні моменти часу. Рішення рівняння (1.2.1) n‑го
порядку визначено однозначно, якщо задані n
так званих початкових умов. Звичайно як початкові умови розглядаються значення xt
при t
= 0, 1,…, n
– 1.
Підставляючи початкові значення xn‑1
,…, x
1
, x
0
і t
= n
як аргументи функції в правій частині (1.2.1), знаходимо xn
; використовуючи знайдене значення й підставляючи тепер xn
, xn‑1
,…, x
2
x
1
і t
= n
+ 1 як аргументи функції, знаходимо xn
+1
, і т. д. Процес може бути продовжений доти, поки не будуть вичерпані всі досліджуємі значення t
.
У моделі економічних циклів Самуельсона-Хікса використовуються кінцево-різницеві рівняння виду xt
= a
1 xt-
1
+ a
2 xt-
2
+ f
(t
) – лінійні кінцево-різницеві рівняння другого порядку, що є приватним видом рівняння (1.2.1).
2. Варіант початкових даних Y0
=0.
Рішення рівняння (1.2.0) проводимо в пакеті MAPLE7 [4]:
> rsolve({f(n)=(2*f (n‑1) – (1*1/4)*f (n‑2)+2), f(0)=0}, f(n));
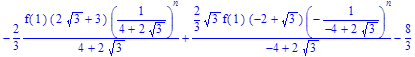 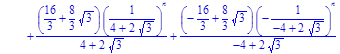
- Samuelson_Hiks3:=simplify(%);
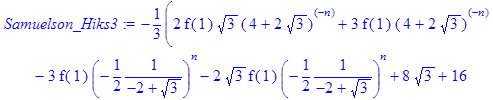 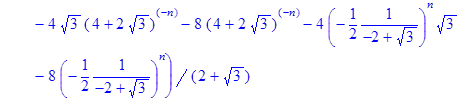
Як показує аналіз рішення для вирішення рівняння моделі Самуельсона-Хікса потрібно 2 послідовні точки початкових умов національного доходу (n‑1, n), тобто 0 та 1 значення для кінечно-різницевої моделі. Тільки тоді з’являється можливість розрахування послідовних значень для точки (n+1). Якщо є тільки одна початкова точка (n‑1), то отриманне рівняння моделі залежить не тільки від значення n, але і від значення Y(1).
3. Варіант початкових даних Y0
=1.
Рішення рівняння (1.2.0) проводимо в пакеті MAPLE7:
> rsolve({f(n)=(2*f (n‑1) – (1*1/4)*f (n‑2)+2), f(0)=1}, f(n));
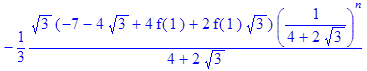 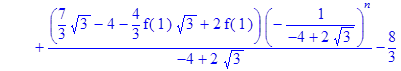 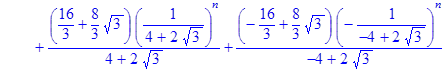
> Samuelson_Hiks3:=simplify(%);
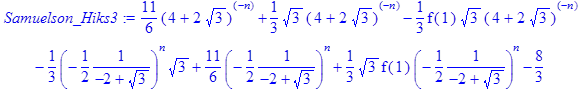
Як показує аналіз рішення для вирішення рівняння моделі Самуельсона-Хікса потрібно 2 послідовні точки початкових умов національного доходу (n‑1, n), тобто 0 та 1 значення для кінечно-різницевої моделі. Тільки тоді з’являється можливість розрахування послідовних значень для точки (n+1). Якщо є тільки одна початкова точка (n‑1), то отримане рівняння моделі залежить не тільки від значення n, але і від значення Y(1).
4. Варіант початкових даних Y0
=0, Y1
=1.
Рішення рівняння (1.2.0) проводимо в пакеті MAPLE7:
> rsolve({f(n)=(2*f (n‑1) – (1*1/4)*f (n‑2)+2), f(0)=0, f(1)=1}, f(n));
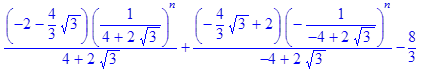 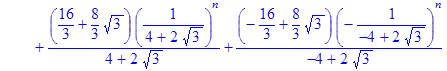
- Samuelson_Hiks3:=simplify(%);
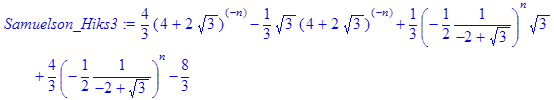
Завдання №3
Попит в та пропозиція S як функції ціни p задаються виразами
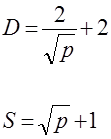 (1.3.0) (1.3.0)
Знайти стаціонарну ціну pD=S
(при умові D=S – вирівнювання попиту та пропозиції) та з’ясувати чи вона є стійкою.
Рішення:
1. Аналіз стійкості рівноважної ціни pD=S
, якщо попит в та пропозиція S завдані функціями:
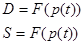 (1.3.1) (1.3.1)
виконується для дискретного підходу за наступним алгоритмом [1].
Нехай ціна близька до рівноважної, при якій попит в дорівнює пропозиції S:
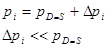 (1.3.2) (1.3.2)
Тоді рівняння (1.3.1) в кінцевих різницях можна представити як:
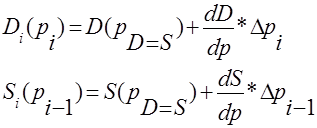 (1.3.3) (1.3.3)
З умови рівноваги попиту та пропозиції та умови (1.3.2), маємо наступне перетворення рівнянь (1.3.3):
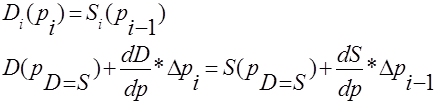 (1.3.4) (1.3.4)
а оскільки
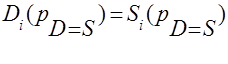 (1.3.5) (1.3.5)
то рівняння (1.3.4) трансформується до вигляду:
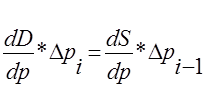 (1.3.6) (1.3.6)
Який перетворюється до наступної форми:
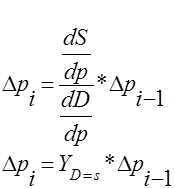 (1.3.7) (1.3.7)
Для приросту ціни ∆pi
отримане рівняння (1.3.7) є характеристичним однорідним різницевим рівнянням з сталим коефіцієнтом. Умова стійкості його розв’язку має вигляд [1]:
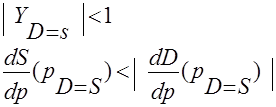 (1.3.8) (1.3.8)
2. Для системи рівнянь (1.3.0) пошук рівноважної ціни PD=S
виконується за схемою:
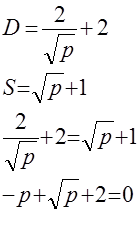 (1.3.9) (1.3.9)
Рішення рівняння (1.3.9) в пакеті MAPLE7 дає рішення:
> solve (– (sqrt(L)*sqrt(L))+sqrt(L)+2=0);
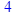
тобто p=4.
3. Знаходимо похідні 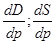 в точці рівноваги р=4: в точці рівноваги р=4:
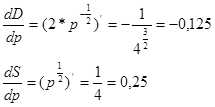 (1.3.10) (1.3.10)
Оскільки умови стійкості для отриманих значень похідних в точці рівноваги не виконуються (1.3.11), то рівноважне рішення р=4 є нестійким
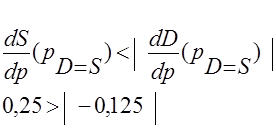 (1.3.11) (1.3.11)
Неперервні динамічні системи
Завдання №1
Найти розв’язок рівняння Харода-Домара
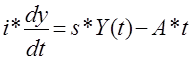
з початковою умовою Y (t=0) =Y0
; s, A, і – const;
Позначення (згідно з моделлю Харода – Домара роста національного доходу держави у часі) [6]:
Y(t) – рівень національного доходу держави у часі;
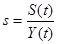 – схильність населення до заощаджень (0< s < 1,0), тобто частка національного доходу, яка відкладується в заощадження; – схильність населення до заощаджень (0< s < 1,0), тобто частка національного доходу, яка відкладується в заощадження;
t – час;
i – коефіцієнт індукованих інвестицій при зміні національного доходу ∆Y(t), тобто частка приросту національного доходу, яка йде на інвестування економіки;
А – рівень незалежних сталих інвестицій
Рішення:
1. У загальному вигляді модель економічного зростання складається із системи п’яти рівнянь [6]:
1) формула виробничої функції, якою передається обсяг потенційного випуску, тобто випуску продукції за умов повної зайнятості;
2) основна макроекономічна тотожність Y
t
=C
t
+I
t
показує, що вимірник випуску (доходу) Y
поділяється в теорії зростання на споживання С
та інвестиції І
; вимірники державних витрат G
і чистого експорту NX
окремо в таких моделях не вирізняються, а розподіляються на споживання та інвестиції держави й інших країн світу (тобто вводяться в компоненти С
та І
);
3) формула розрахунку динаміки обсягу капіталу з урахуванням інвестицій та амортизації основного капіталу (за умови нульового інвестиційного лагу) має вигляд:
K
t
=K
t-1
+I
t
–W
t,
де K
t
– запас капіталу наприкінці періоду t
;
І
t
– інвестиції за весь період t
;
W
t,
– амортизація капіталу за період t
.
Наведена формула вказує на те, що кількість капіталу зростає на величину інвестицій та зменшується на величину амортизаційних відрахувань;
4) формула для розрахунку вибуття капіталу (амортизації) має вигляд:
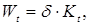
де 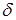 – постійна (незмінна) норма амортизації, яка задається екзогенно отже, вважається, що вибуття капіталу є пропорційним до величини його запасу; – постійна (незмінна) норма амортизації, яка задається екзогенно отже, вважається, що вибуття капіталу є пропорційним до величини його запасу;
5) щодо інвестицій, то передбачається, що вони складають постійний процент від випуску I
t
= s
*
Y
t
, де s
– норма інвестицій (частка інвестицій у сукупному продукті (доході). Норма інвестицій s
збігається з нормою заощадження, оскільки сукупні заощадження S
t
дорівнюють сукупним інвестиціям І
t
. Відповідно, Y
t
=C
t
+S
t
=C
t
+I
t.
Таким чином, модель економічного зростання у загальному вигляді складається із системи п’яти наведених рівнянь, які містять сім змінних (Y, K, L, C, I, 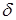 , s
), три із яких задаються екзогенно: , s
), три із яких задаються екзогенно:
— затрати праці L
(зростають із постійним темпом n
);
— норма амортизації основного капіталу 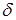 ; ;
— норма заощадження s (задається безпосередньо або ж у вигляді певних умов, наприклад, максимізація споживання).
Мета дослідників – з’ясувати питання про те, як змінюються ендогенні змінні в моделі економічного зростання (Y
, C
та І
) і який із чинників є визначальним фактором довгострокового економічного зростання.
Модель економічного зростання Харода–Домара
Це найпростіша модель економічного зростання, і була вона розроблена наприкінці 40‑х рр. Модель описує динаміку доходу (Y
), який є сумою споживчих (С
) та інвестиційних (І
) витрат. Економіка вважається закритою, тому чистий експорт (NX
) дорівнює нулю, а державні витрати (G
) в моделі не вирізняються. Основним фактором зростання є нагромадження капіталу.
Основні передумови моделі:
– постійна продуктивність капіталу MPK = dY/dK
;
– постійна норма заощадження s = I/Y
;
– відсутній процес вибуття капіталу W = 0
;
– інвестиційний лаг дорівнює нулеві, тобто інвестиції миттєво переходять у приріст капіталу. Формально це означає, що dK(t) = I(t)
;
– модель не враховує технічного прогресу;
— випуск не залежить від затрат праці, оскільки праця не є дефіцитним ресурсом;
— використовується виробнича функція Леонтьєва, яка передбачає неможливість взаємозаміни акторів виробництва – праці і капіталу.
Припускається, що швидкість доходу пропорційна інвестиціям: dY = MPK
*
I(t) = MPK
*
s
*
Y,
а темп приросту доходу dY/Y
*
dt
є постійним і дорівнює s
*
MPK
. Він прямо пропорційний нормі заощаджень та граничній продуктивності капіталу. Інвестиції (І
) та споживання (С
) в моделі Харода-Домара зростають з таким же постійним темпом (s
*
MPK
).
2. Рішення проводимо в пакеті MAPLE7, використовуючи функцію вирішення диференційного рівняння з початковими умовами Y (t=0)=Y0
:
> L6:=diff (y(t), t)=(s/i*y(t) – A/i*t);
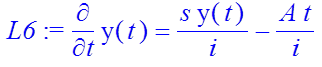
- ans1:= dsolve({L6, y(0)=Y0}, y(t));
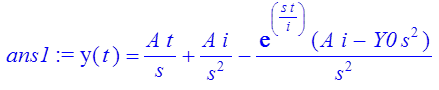
Таким чином, розв’язком рівняння Харода-Домара у вигляді
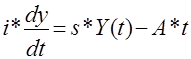
з початковою умовою Y (t=0) =Y0
; s, A, і – const;
є функція:
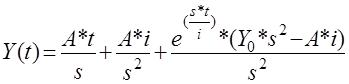
Завдання №2
Попит в та пропозиція S як функції змінної в часі ціни p=F(t) та її похідних задаються виразами
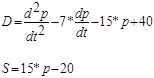 (2.2.0) (2.2.0)
Знайти стаціонарну ціну рівноваги попиту та пропозиції pD=S
(t) – при умові D=S – вирівнювання попиту та пропозиції, як функцію часу, та з’ясувати чи вона є стійкою (оцінити рівень динаміки похідної 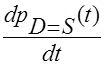 ). ).
Рішення:
1. Якщо попит в та пропозиція S є функціями ціни p(t) та її першої та другої похідних  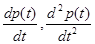 , то їх рівняння в загальному вигляді можна представити наступним чином [1]: , то їх рівняння в загальному вигляді можна представити наступним чином [1]:
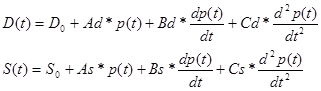 (2.2.1) (2.2.1)
2. В умовах пошуку точок рівноваги попиту та пропозиції:
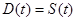 (2.2.2) (2.2.2)
рівняння (2.2.1), віднімаючи перше від другого, перетворюємо у наступне рівняння
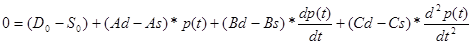 (2.2.3) (2.2.3)
яке має наступні початкові умови:
 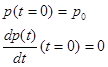 (2.2.4) (2.2.4)
Загальний розв’язок рівнянь (2.2.1) – (2.2.4) має вигляд [1]:
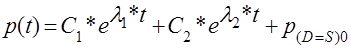 (2.2.5) (2.2.5)
де С1 та С2 – довільні сталі;
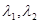 – корені характеристичного рівняння: – корені характеристичного рівняння:
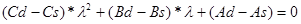 (2.2.6) (2.2.6)
Після вирішення рівняння (2.2.6), отримані 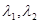 – корені характеристичного рівняння в рівнянні (2.2.5) характеризують стаціонарність рівноважної ціни p(t) наступним чином: – корені характеристичного рівняння в рівнянні (2.2.5) характеризують стаціонарність рівноважної ціни p(t) наступним чином:
1) Якщо обидва корені 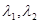 – є дійсними від’ємними або комплексними з від’ємною дійсною частиною, то рівняння (2.2.5) перетворюється до вигляду: – є дійсними від’ємними або комплексними з від’ємною дійсною частиною, то рівняння (2.2.5) перетворюється до вигляду:
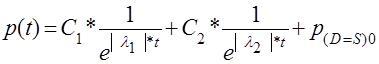 (2.2.7) (2.2.7)
та з наростанням t рівноважна ціна p(t) буде прямувати до ціни рівноваги попиту в та S – PD=S,
оскільки 1 та другий член рівняння (2.2.7) будуть наближатися до нуля.
2) Якщо обидва корені 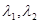 – є дійсними позитивними, або один з них має позитивний знак, або комплексними з позитивною дійсною частиною, то згідно рівнянь (2.2.5), (2.2.7) з наростанням t рівноважна ціна p(t) буде віддалятися від до ціни рівноваги попиту в та S – PD=S,
оскільки або перший, або другий член рівняння (2.2.5) будуть наближатися до – є дійсними позитивними, або один з них має позитивний знак, або комплексними з позитивною дійсною частиною, то згідно рівнянь (2.2.5), (2.2.7) з наростанням t рівноважна ціна p(t) буде віддалятися від до ціни рівноваги попиту в та S – PD=S,
оскільки або перший, або другий член рівняння (2.2.5) будуть наближатися до  . .
3. В точці рівноваги попиту та пропозиції D=S, рівняння (2.2.0) перетворюються в наступне диференційне рівняння другого порядку похідних:
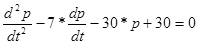 (2.2.8) (2.2.8)
Для пошуку точок стаціонарної ціни рівноваги pD=S
враховуємо умови дорівнювання нулю першої та другої похідної в цих точках:
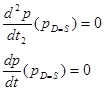 (2.2.9) (2.2.9)
тоді рівняння (2.2.8) перетворюється до вигляду, який дозволяє розрахувати значення стаціонарної ціни рівноваги попиту та прозиції:
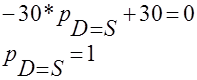 (2.2.10) (2.2.10)
Для рівняння (2.2.8) характеристичне рівняння має наступний вигляд:
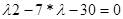 (2.2.11) (2.2.11)
а корені його рішення, розраховані в пакеті MAPLE7, дорівнюють
> solve (L*L‑7*L‑30);
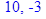
Оскільки корені характеристичного рівняння (2.2.11) 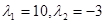 дійсні та мають різні знаки – рішення рівняння (2.2.10) є нестійким. дійсні та мають різні знаки – рішення рівняння (2.2.10) є нестійким.
Завдання №3
Знайти стаціонарні точки динамічної системи
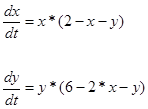 (2.3.0) (2.3.0)
та дослідити їх стійкість в лінійному наближенні.
Рішення:
1. Положення рівноваги вихідної динамічної системи (стаціонарні точки динамічної системи) визначається наступними умовами:
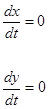 (2.3.1) (2.3.1)
звідкіля маємо систему рівнянь рівноваги
 (2.3.2) (2.3.2)
Рішення системи рівнянь рівноваги (2.3.2) в пакеті MAPLE7 дає наступні 4 пари коренів – стаціонарних точок рівноваги динамічної системи (2.3.0):
> eqp1:=-x*x+2*x-x*y=0;
> eqp2:=-y*y+6*y‑2*x*y=0;
>
> solve({eqp1, eqp2}, {x, y});


 (2.3.3) (2.3.3)
2. Для дослідження стійкості кожного з отриманих рішень, складаємо системи першого наближення в околицях точок рівноваги за допомогою розкладення в ряд Тейлора. Формула Тейлора для функції двох змінних x, y у першому наближенні (тільки рівень 1 похідних) для функції  в околицях точки x0
, y0
має наступний вигляд [7]: в околицях точки x0
, y0
має наступний вигляд [7]:
 (2.3.4) (2.3.4)
Побудову систем рівнянь першого наближення системи (2.3.2) виконуємо за допомогою пакета MAPLE7 [4]:
> DxDt:=-x*x+2*x-x*y;

> mtaylor (DxDt, [x=0, y=0], 2);
> mtaylor (DxDt, [x=2, y=0], 2);
> mtaylor (DxDt, [x=4, y=-2], 2);
> mtaylor (DxDt, [x=0, y=6], 2);



 (2.3.5) (2.3.5)
> DyDt:=-y*y+6*y‑2*x*y;
> mtaylor (DyDt, [x=0, y=0], 2);
> mtaylor (DyDt, [x=2, y=0], 2);
> mtaylor (DyDt, [x=4, y=-2], 2);
> mtaylor (DyDt, [x=0, y=6], 2);
>




 (2.3.6) (2.3.6)
6. Використовуючи отримані результати (2.3.5), (2.3.6), дослідження стійкості рішення для 4‑х пар коренів проводимо в наступній послідовності [5]:
6.1. 1 пара коренів – x=0, y=0
Cистема характеристичних рівнянь 1‑го наближення ряду Тейлора відносно точки (x=0, y=0) має вигляд:

Для знаходження умов стійкості будуємо характеристичну матрицю:
 
 
Звідки характеристичне рівняння 
Корені рішення цього рівняння  та та  є дійсні та мають однакові знаки, що відповідає стійкості рішення рівноваги [5] в точці (x=0, y=0). є дійсні та мають однакові знаки, що відповідає стійкості рішення рівноваги [5] в точці (x=0, y=0).
Пара коренів – x=2, y=0
Cистема характеристичних рівнянь 1‑го наближення ряду Тейлора відносно точки (x=2, y=0) має вигляд:

Виконуючи заміну змінних в системі () на

отримуємо модифіковану систему рівнянь:

Для знаходження умов стійкості будуємо характеристичну матрицю:
 
 
Звідки характеристичне рівняння

Вирішуємо рівняння () в пакеті MAPLE7
> L2:=a*a+0*a‑2=0;
>

> solve(L2);

Корені рішення цього рівняння  та та  є дійсні та мають різні знаки, що відповідає нестійкості рішення рівноваги [5] в точці (x=2, y=0). є дійсні та мають різні знаки, що відповідає нестійкості рішення рівноваги [5] в точці (x=2, y=0).
3 пара коренів – x=4, y=-2
Cистема характеристичних рівнянь 1‑го наближення ряду Тейлора відносно точки (x=0, y=6) має вигляд:

Виконуючи заміну змінних в системі () на

отримуємо модифіковану систему рівнянь:

Для знаходження умов стійкості будуємо характеристичну матрицю:
 
 
Звідки характеристичне рівняння

Вирішуємо рівняння () в пакеті MAPLE7
> solve (L*L+2*L+8);

Корені рішення цього рівняння  та та  є комплексні та мають однакові негативні знаки при дійсній частині, що відповідає стійкості рішення рівноваги [5] в точці (x=4, y=-2). є комплексні та мають однакові негативні знаки при дійсній частині, що відповідає стійкості рішення рівноваги [5] в точці (x=4, y=-2).
Пара коренів – x=0, y=6
Cистема характеристичних рівнянь 1‑го наближення ряду Тейлора відносно точки (x=4, y=-2) має вигляд:

Виконуючи заміну змінних в системі () на

отримуємо модифіковану систему рівнянь:

Для знаходження умов стійкості будуємо характеристичну матрицю:
 
 
Звідки характеристичне рівняння

Корені рішення цього рівняння  та та  є дійсними та мають знак (–) при дійсній частині, що відповідає асимптотичній стійкості рішення рівноваги [5] в точці (x=4, y=-2). є дійсними та мають знак (–) при дійсній частині, що відповідає асимптотичній стійкості рішення рівноваги [5] в точці (x=4, y=-2).
|