|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВПО
Всероссийский заочный финансово-экономический институт
Филиал в г. Архангельске
Кафедра экономико-математических методов и моделей
ЛАБОРАТОРНАЯ РАБОТА
по дисциплине «эконометрика»
Вариант №5
Выполнила студентка
3 курса группы №2 «периферия»
специальности «финансы и кредит»
№ л/д:07ФФД10522
Лукина Мария Александровна
Проверил преподаватель
Бан Татьяна Михайловна
Архангельск – 2010
Постановка задачи
Наименование задачи
: анализ предприятий одной отрасли РФ – 1.
Цель задачи
– проанализировать экономическую деятельность предприятий.
Условие задачи
: имеются данные (см. таб. 1) об экономической деятельности предприятий одной отрасли РФ в 1997г.:
Y – прибыль от реализации продукции, млн. руб.;
X1
– численность промышленно – производственного персонала, чел.;
X3
– среднегодовая стоимость основных фондов, млн. руб.;
X4
– электровооружённость, кВт∙ч;
X5
– техническая вооружённость одного рабочего, млн. руб.
| № наблюдения
|
Прибыль от реализации продукции, млн. руб.
|
Численность промышленно-производствен-ного персонала, чел.
|
Среднегодовая стоимость основных фондов, млн. руб.
|
Электровоору-женность, кВт×ч.
|
Техническая вооруженность одного рабочего, млн. руб.
|
|
|
Y
|
X1
|
X3
|
X4
|
X5
|
| 1
|
7960
|
864
|
16144
|
4,9
|
3,2
|
| 2
|
42392
|
8212
|
336472
|
60,5
|
20,4
|
| 3
|
9948
|
1866
|
39208
|
24,9
|
9,5
|
| 4
|
15503
|
1147
|
63273
|
50,4
|
34,7
|
| 5
|
9558
|
1514
|
31271
|
5,1
|
17,9
|
| 6
|
10919
|
4970
|
86129
|
35,9
|
12,1
|
| 7
|
2631
|
1561
|
48461
|
48,1
|
18,9
|
| 8
|
18727
|
4197
|
138657
|
69,5
|
12,2
|
| 9
|
18279
|
6696
|
127570
|
31,9
|
8,1
|
| 10
|
39689
|
5237
|
208900
|
139,4
|
29,7
|
| 11
|
-984
|
547
|
6922
|
16,9
|
5,3
|
| 12
|
5431
|
710
|
8228
|
17,8
|
5,6
|
| 13
|
2861
|
940
|
18894
|
27,6
|
12,3
|
| 14
|
-1123
|
3528
|
27486
|
13,9
|
3,2
|
| 15
|
203892
|
52412
|
1974472,00
|
37,3
|
19
|
| 16
|
16304
|
4409
|
162229
|
55,3
|
19,3
|
| 17
|
35218
|
6139
|
128731
|
35,1
|
12,4
|
| 18
|
857
|
802
|
6714
|
14,9
|
3,1
|
| 19
|
116
|
442
|
478
|
0,2
|
0,6
|
| 20
|
1021
|
2797
|
60209
|
37,2
|
13,1
|
| 21
|
102843
|
10280
|
540780
|
74,45
|
21,5
|
| 22
|
10035
|
4560
|
108549
|
32,5
|
13,2
|
| 23
|
6612
|
3801
|
169995
|
75,9
|
27,2
|
| 24
|
163420
|
46142
|
972349
|
27,5
|
10,8
|
| 25
|
2948
|
2535
|
163695
|
65,5
|
19,9
|
Таб.1. Исходные данные
Задание
1. Рассчитать параметры линейного уравнения множественной регрессии с полным перечнем факторов.
2. Оценить статистическую значимость параметров регрессионной модели с помощью t – критерия, проверить нулевую гипотезу о значимости уравнения с помощью F – критерия (α=0,05), оценить качество уравнения регрессии с помощью коэффициента детерминации.
3. Отобрать информативные факторы в модель по t – критерию для коэффициентов регрессии. Построить модель только с информативными факторами и оценить её параметры. Дать оценку влияния значимых факторов на результат с помощью коэффициентов эластичности, β- и Δ – коэффициентов.
4. Рассчитать прогнозные значения результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
1. Рассчитаем параметры линейного уравнения множественной регрессии с полным перечнем факторов, используя инструмент «регрессия» пакета анализа. В массив «входной интервал Y» вводим диапазон ячеек, содержащих значения результата Y – B2:B27; в массив «входной интервал X» вводим диапазон ячеек, содержащих значения фактора X – C2:D27, активизируем флажки «метки», «новый рабочий лист» и «остатки», затем нажимаем клавишу «ок».
В результате получаем следующее линейное уравнение множественной регрессии:
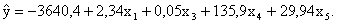
2а. Оценим статистическую значимость параметров регрессионной модели с помощью t – критерия. Фактор xj
является статистически значимым, если параметр aj
при этом факторе значим. Для проверки значимости параметра aj
используем столбец «t – статистка» таблицы 4 дисперсионного анализа приложения 2.
Имеем:

Сравним расчётные значения t – критерия с табличным значением tтабл.
=2,064.
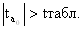 , значит, параметр a0
незначим. , значит, параметр a0
незначим.
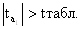
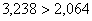 , значит, параметр a1
значим, и фактор x1
при данном параметре является статистически значимым, его следует включить в модель. , значит, параметр a1
значим, и фактор x1
при данном параметре является статистически значимым, его следует включить в модель.
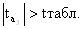
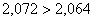 , значит, параметр a3
значим и фактор x3 , значит, параметр a3
значим и фактор x3
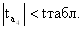
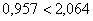 , значит, параметр a4
незначим, и фактор x4
при данном параметре не является статистически значимым, его следует исключить из модели. , значит, параметр a4
незначим, и фактор x4
при данном параметре не является статистически значимым, его следует исключить из модели.
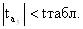
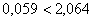 , значит, параметр a4
незначим, и фактор x4
при данном параметре не является статистически значимым, его следует исключить из модели. , значит, параметр a4
незначим, и фактор x4
при данном параметре не является статистически значимым, его следует исключить из модели.
2б. Проверим нулевую гипотезу о значимости уравнения с помощью F – критерия (α=0,05). Для этого находим расчётное значение данного критерия с помощью функции «FРАСПОБР» мастера функций Excel: в массив «вероятность» вводим значение уровня значимости α=0,05, в массив «число степеней свободы1» вводим значение k1
=m=2 (т.к. в модели 2 фактора: х 1
и х 3
), в массив «число степеней свободы2» вводим значение k2
=n-m-1=25-2-1=24. Затем полученное расчётное значение Fрасч.=3,403 сравниваем с табличным значением Fтабл.=80,419, которое берём из столбца «F» таблицы 4 дисперсионного анализа.
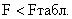
3,403<80,419, значит, уравнение регрессии незначимо.
2в. Проверим качество уравнения регрессии с помощью коэффициента детерминации по следующей формуле по данным таблицы 7(см. приложение 3):
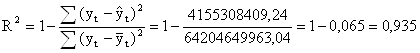 , ,
значит, построенная линейная модель множественной регрессии точная, а значит, и качественная.
3а. Отобранные информативные факторы в модель по t - критерию для коэффициентов регрессии представлены в таблице 6 приложения 3. Построим модель только с информативными факторами x1
и x3
, используя инструмент «регрессия» пакета анализа данных (см. приложение 5).
В результате получаем следующее линейное уравнение множественной регрессии:
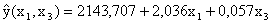 . .
3б. Оценим влияние значимых факторов на результат с помощью коэффициентов эластичности, β- и Δ-коэффициентов. Вычислим коэффициент эластичности для фактора х1 последующей формуле:
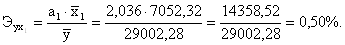 - -
если фактор х1
увеличить на 1%, то результат y увеличится на 50%.
Аналогично находим коэффициент эластичности для фактора х3
:
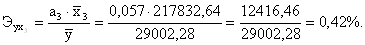 - -
если фактор х3
увеличить на 1%, то результат y увеличится на 42%.
Находим β-коэффициенты. Для этого сначала вычислим СКО x1
и x3
, используя функцию СТАНДОТКЛОН мастера функций Excel. В ячейку С32 вводим формулу:
= СТАНДОТКЛОН (С7:С31).
Аналогичную формулу вводим в ячейку D32 для нахождения СКО для фактора х3
:
= СТАНДОТКЛОН(D7: D31).
Полученные значения Sxj
подставим в формулы (*) и (**). В ячейку С35 вводим формулу:
=G35*C32/B32.
В ячейку D35 вводим формулу:
=H35*D32/B32.
 (*) (*)
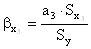 .(**) .(**)
Получаем:
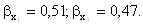
Если фактор х1
увеличить на Sx1
=12994,033, то результат y изменится на
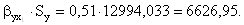
Если фактор х3
увеличить на Sx3
=422015,64, то результат изменится на
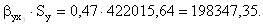
Для нахождения Δ-коэффициента вычислим сначала коэффициент парной корелляции, используя инструмент «корелляция» пакета анализа данных, затем его значения подставляем в формулу:
 . .
В ячейку С36 вводим формулу:
=0,956*С35/0,935.
Получаем: 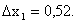 , значит, 50% влияния оказывает фактор х1
. , значит, 50% влияния оказывает фактор х1
.
Аналогично находим Δ-коэффициент для фактора х3
. В ячейку D36 вводим формулу:
=0,954*D35/0,935.
Получаем: 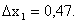 , значит, 47% влияния оказывает фактор х3
. , значит, 47% влияния оказывает фактор х3
.
4. Найдём прогнозные значения результата y, если прогнозные значения факторов x составляют 80% от их максимальных значений.
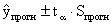 - интервальный прогноз. - интервальный прогноз.
 - средняя квадратическая ошибка прогноза. - средняя квадратическая ошибка прогноза.
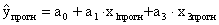
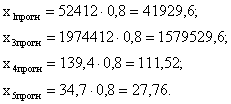
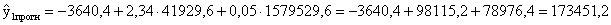 - точечный прогноз. - точечный прогноз.
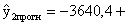
|