КОНТРОЛЬНАЯ РАБОТА
ПО ДИСЦИПЛИНЕ
«Математическая статистика»
Задания к контрольной работе
1. Генеральная совокупность. Выборка. Объем выборки. Среднее значение. Дисперсия. Среднеквадратическое отклонение.
2. Найти коэффициент эластичности для указанной модели в заданной точке X. Сделать экономический вывод. Модель :  ; X = 4; ; X = 4;
3. Для представленных данных выполнить следующее задание:
3.1 Провести эконометрический анализ линейной зависимости показателя от первого фактора. Сделать прогноз для любой точки из области прогноза, построить доверительную область. Найти коэффициент эластичности в точке прогноза.
3.2 Провести эконометрический анализ нелинейной зависимости показателя от второго фактора, воспользовавшись подсказкой. Сделать прогноз для любой точки из области прогноза, построить доверительную область. Найти коэффициент эластичности в точке прогноза.
3.3 Провести эконометрический анализ линейной зависимости показателя от двух факторов. Сделать точечный прогноз для любой точки из области прогноза. Найти частичные коэффициенты эластичности в точке прогноза.
Производительность труда, фондоотдача и уровень рентабельности по хлебозаводам области за год характеризуются следующими данными:
| № завода
|
Фактор
|
Уровень рентабельности,
%
|
| Фондоотдача, грн
|
Производительность труда, грн
|
| 1
|
38,9
|
3742
|
10,7
|
| 2
|
33,3
|
2983
|
11,3
|
| 3
|
37,7
|
3000
|
12,2
|
| 4
|
31,1
|
2537
|
12,4
|
| 5
|
29,4
|
2421
|
10,9
|
| 6
|
37,2
|
3047
|
11,3
|
| 7
|
35,6
|
3002
|
11,1
|
| 8
|
34,1
|
2887
|
14,0
|
| 9
|
16,1
|
2177
|
6,8
|
| 10
|
22,8
|
2141
|
7,1
|
| 11
|
21,7
|
2005
|
8,9
|
| 12
|
26,8
|
1843
|
4,2
|
| 13
|
23,3
|
2031
|
7,4
|
| 14
|
24,5
|
2340
|
11,4
|
| 15
|
19,9
|
1933
|
4,8
|
Нелинейную зависимость принять 
1. Генеральная совокупность. Выборка. Объем выборки. Среднее значение. Дисперсия. Среднеквадратическое отклонение
Генеральная совокупность - вся изучаемая выборочным методом статистическая совокупность объектов и/или явлений общественной жизни, имеющих общие качественные признаки или количественные переменные.
Выборочная совокупность (выборка)- часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение о всей генеральной совокупности.
Для того, чтобы заключение, полученное путем изучения выборки
, можно было распространить на всю генеральную совокупность выборка должна обладать свойством репрезентативности.
Объем выборки - общее число единиц наблюдения в выборочной совокупности. Определение объема выборки представляет собой один из основных этапов ее формирования. Объем выборки для генеральной совокупности обозначается– N, для выборки – n.
Среднее значение выборки можно вычислить по формуле:

Дисперсия (от лат. dispersio - рассеяние), в математической статистике и теории вероятностей, наиболее употребительная мера рассеивания, т. е. отклонения от среднего. Дисперсия вычисляется по формуле:
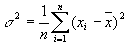 - простая дисперсия,
- простая дисперсия,
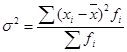 - взвешенная дисперсия. - взвешенная дисперсия.
Дисперсия есть средняя величина квадратов отклонений. Для этого достаточно извлечь из дисперсии корень второй степени, получится среднее квадратическое отклонение (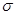 ). ).
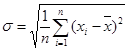
или
 . .
Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности.
2. Найти коэффициент эластичности для указанной модели в заданной точке
X
. Сделать экономический анализ
Известно, что коэффициент эластичности показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %. Формула расчета коэффициента эластичности:
 Э = f′(x)X/Y, Э = f′(x)X/Y,
где f′(x) – первая производная, характеризующая соотношение прироста результата и фактора для соответствующей формы связи.
 , ,
 . .
Следовательно получим следующее математическое выражение
 . .
При заданном значении X=4 получим, что коэффициент эластичности равен Э=0,25.
Допустим, что заданная функция  определяет зависимость спроса от цены. В этом случае с ростом цены на 4% спрос повысится в среднем на 0,25 %. определяет зависимость спроса от цены. В этом случае с ростом цены на 4% спрос повысится в среднем на 0,25 %.
3. Производительность труда, фондоотдача и уровень рентабельности по хлебозаводам области за год характеризуются следующими данными:
| № завода
|
Фактор
|
Уровень рентабельности,
%
|
| Фондоотдача, грн
|
Производительность труда, грн
|
| 1
|
38,9
|
3742
|
10,7
|
| 2
|
33,3
|
2983
|
11,3
|
| 3
|
37,7
|
3000
|
12,2
|
| 4
|
31,1
|
2537
|
12,4
|
| 5
|
29,4
|
2421
|
10,9
|
| 6
|
37,2
|
3047
|
11,3
|
| 7
|
35,6
|
3002
|
11,1
|
| 8
|
34,1
|
2887
|
14,0
|
| 9
|
16,1
|
2177
|
6,8
|
| 10
|
22,8
|
2141
|
7,1
|
| 11
|
21,7
|
2005
|
8,9
|
| 12
|
26,8
|
1843
|
4,2
|
| 13
|
23,3
|
2031
|
7,4
|
| 14
|
24,5
|
2340
|
11,4
|
| 15
|
19,9
|
1933
|
4,8
|
Нелинейную зависимость принять 
Последовательность выполнения задания 3
1. Вводим данные .Определяем основные числовые характеристики.
2. Строим диаграмму рассеивания (корреляционное поле).
3. Определяем тесноту линейной связи по коэффициенту корреляции.
4. Строим линейную модель вида у = bо + b1
*х.
5. Определяем общее качество модели по коэффициенту детерминации R2
. Проверяем полученную модель на адекватность по критерию Фишера
6. Проверяем статистическую значимость коэффициентов модели.
7. По полученной модели рассчитываем значение показателя Y для всех точек выборки и в точке прогноза (точку прогноза выбираем произвольно из области прогноза).
8. Рассчитаем полуширину доверительного интервала d. =
 
9. Рассчитаем доверительный интервал для всех точек выборки и в точке прогноза: (Y-d, Y +d).
10. Рассчитываем коэффициент эластичности:
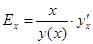 Для линейной модели y’
х
= b1
. Получим Для линейной модели y’
х
= b1
. Получим
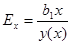 , где у(х) - рассчитанное по модели значение показателя. , где у(х) - рассчитанное по модели значение показателя.
11. Строим, используя «Мастер диаграмм», корреляционное поле, график эластичности и доверительную область.
12. Делаем лист с формулами.
Решение 1:
1. Вводим данные. Определяем основные статистики. Строим корреляционное поле. По виду корреляционного поля выдвигаем гипотезу о нелинейной зависимости между X и Y.
2. С помощью формул перехода линеаризуем нелинейную модель:  , V=у. Получаем линейную модель относительно новых переменных , V=у. Получаем линейную модель относительно новых переменных
V = b0
+ b1
u
3. Рассчитываем основные числовые характеристики X, Y, V, U с помощью «Мастера функций» и функции «Описательная статистика».
4. Продолжим регрессионный анализ с помощью вкладки «Анализ данных» и функции «Регрессия».
5. Вычислим значения V(U),V min, V max.
6. Рассчитаем полуширину доверительного интервала в .
7. По формулам обратного перехода пересчитываем значения Y, Ymin (левая граница доверительного интервала»,Ymaх(правая граница доверительного интервала).
8. Рассчитываем коэффициент эластичности
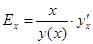 , ,
9. Строим доверительные области V(U) и Y(х) и график эластичности.
10. Делаем лист с формулами.
Решение 2:
1. Вводим данные.
2. Определяем основные статистики.
3. По корреляционной таблице проверяем факторы на коллинеарность.
4. Строим линейную модель вида y = b0
+b1
х+b2
х.
5. Определяем общее качество модели по коэффициенту детерминации R2
. Проверяем полученную модель на адекватность по критерию Фишера.
6. Проверяем статистическую значимость коэффициентов модели.
7. По полученной модели рассчитываем значения показателя Y для всех точек выборки и в точке прогноза(точку прогноза выбрали произвольно из области прогноза).
8. Рассчитываем частичные коэффициенты эластичности:
- по фактору X1

- по фактору Х2
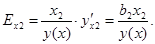
4. Экономический анализ
Обозначим Фондоотдачу (грн.) – Х, Уровень рентабельности (%) – Y. Найдем основные числовые характеристики.
Объем выборки n=15 ‑ суммарное количество наблюдений.
Фондоотдача изменяется от 16,1 до 38,9 грн., уровень рентабельности изменяется от 4,2 до 14%.
Среднее значение фондоотдачи составляет 28,83 грн, среднее значение уровня рентабельности составляет 9,63%.
Среднее значение можно вычислить по формуле: 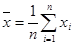 . .
Дисперсия 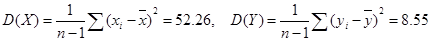 . .
Среднеквадратическое отклонение 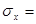 7,23, значит среднее отклонение фондоотдачи от среднего значения, составляет 7,23 грн., 7,23, значит среднее отклонение фондоотдачи от среднего значения, составляет 7,23 грн., 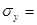 2,92, значит среднее отклонение уровня рентабельности от среднего значения, составляет 2,92%. 2,92, значит среднее отклонение уровня рентабельности от среднего значения, составляет 2,92%.
Определим, связаны ли X и У между собой, и, если да, то определить формулу связи.
По таблице строим корреляционное поле (диаграмму рассеивания) - нанесем точки (X, Y) на график. Точка с координатами (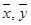 ) =(28,83;9.63) называется центром рассеяния. ) =(28,83;9.63) называется центром рассеяния.
По виду корреляционного поля можно предположить, что зависимость между Y и X линейная.
Для определения тесноты линейной связи найдем коэффициент корреляции (из таблицы регрессионная статистика):
 . .
Так как  , то линейная связь между X и Y достаточная. , то линейная связь между X и Y достаточная.
Пытаемся описать связь между X и Y зависимостью  . .
Параметры  находим по методу наименьших квадратов. находим по методу наименьших квадратов.
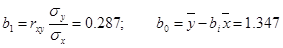
Так как  , то зависимость между X и Y прямая: с ростом фондоотдачи уровень рентабельности повышается. Проверим значимость коэффициентов , то зависимость между X и Y прямая: с ростом фондоотдачи уровень рентабельности повышается. Проверим значимость коэффициентов  . .
Значимость коэффициента может быть проверена с помощью критерия Стьюдента:
 . .
Значимость 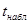 равна равна 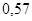 . Это меньше 5%. Коэффициент . Это меньше 5%. Коэффициент 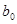 статистически значим. статистически значим.
 . .
Значимость 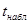 равна равна 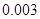 , что практически равно 0%. Это меньше 5%. Коэффициент , что практически равно 0%. Это меньше 5%. Коэффициент 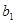 статистически значим. статистически значим.
Проверим модель на адекватность. Проанализировав таблицу Дисперсионный анализ можно сказать, разброс данных, объясняемый регрессией  . Остатки, необъясненный разброс . Остатки, необъясненный разброс  . Общий разброс данных . Общий разброс данных  . Коэффициент детерминации . Коэффициент детерминации 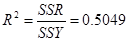 . Разброс данных объясняется на 50,49% линейной моделью и на 49,51% - случайными ошибками. . Разброс данных объясняется на 50,49% линейной моделью и на 49,51% - случайными ошибками.
Проверим модель с помощью критерия Фишера. Для проверки найдем величины: 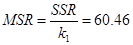 и и 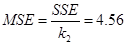 . Вычисляем . Вычисляем 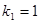 и и  . Находим наблюдаемое значение критерия Фишера . Находим наблюдаемое значение критерия Фишера 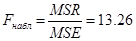 . Значимость этого критерия . Значимость этого критерия  , т.е. процент ошибки практически равен 0%, что меньше чем 5%. Модель , т.е. процент ошибки практически равен 0%, что меньше чем 5%. Модель 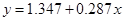 считается адекватной с гарантией более 95%. считается адекватной с гарантией более 95%.
Найдем прогноз.
Примем за точку прогноза значение фондоотдачи 33 грн.
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза:
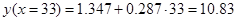 . .
Построим доверительную область для точки прогноза и всех точек.
Найдем полуширину доверительного интервала в каждой точке выборки:
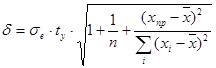 , ,
где 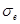 - среднеквадратическое отклонение выборочных точек от линии регрессии; - среднеквадратическое отклонение выборочных точек от линии регрессии;  ; ;
 ‑ критическая точка распределения Стьюдента для надежности ‑ критическая точка распределения Стьюдента для надежности  и и  ; ; 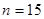 . .
Прогнозируемый доверительный интервал для любого x такой  , где , где 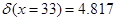 , т.е. доверительный интервал для , т.е. доверительный интервал для  составит от 6,0157 до 15,6503 с гарантией 95%., т.е. при фондоотдаче 33 грн. Уровень рентабельности составит от 6,0157% до 15,6503%. составит от 6,0157 до 15,6503 с гарантией 95%., т.е. при фондоотдаче 33 грн. Уровень рентабельности составит от 6,0157% до 15,6503%.
Найдем эластичность.
Для линейной модели 
Коэффициент эластичности показывает, что при изменении фондоотдачи на 1% уровень рентабельности увеличится с 10,83% на 0,876%. Т.е. при увеличении фондоотдачи рентабельность растет.
Задание № 3.2
Обозначим производительность труда в расчете на одного работника (грн.) – Х, Уровень рентабельности (%) – Y. Построим нелинейную зависимость показателя от фактора вида  . Проанализируем фактор X, используя таблицу описательная статистика. . Проанализируем фактор X, используя таблицу описательная статистика.
Производительность труда в расчете на одного работника изменяется от 1843 до 3742 грн. Средняя производительность составляет 2535,27 грн. Отклонение от среднего составляет 546,96.
Определим, связаны ли X и У между собой, и, если да, то определить формулу связи.
По таблице строим корреляционное поле (диаграмму рассеивания) - нанесем точки (X, Y) на график.
По виду корреляционного поля можно предположить, что зависимость между Y и X нелинейная.
Пытаемся описать связь между X и Y зависимостью  . .
Перейдем к линейной модели. Делаем линеаризующую подстановку:  . Получим новые данные U и V. Для этих данных строим линейную модель: . Получим новые данные U и V. Для этих данных строим линейную модель: 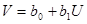 . Проверим тесноту линейной связи U и V. Найдем коэффициент корреляции (из таблицы Регрессионная статистика): . Проверим тесноту линейной связи U и V. Найдем коэффициент корреляции (из таблицы Регрессионная статистика): 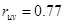 .Между U и V достаточная связь. .Между U и V достаточная связь.
Параметры  находим по методу наименьших квадратов. находим по методу наименьших квадратов.
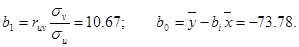
Значимость коэффициента может быть проверена с помощью критерия Стьюдента:
 . .
Значимость 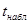 равна 0,0021, что практически равно 0%. Это меньше 5%. Коэффициент равна 0,0021, что практически равно 0%. Это меньше 5%. Коэффициент 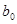 статистически значим. статистически значим.
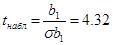 . .
Значимость 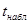 равна0,00083, что практически равно 0%. Это меньше 5%. Коэффициент равна0,00083, что практически равно 0%. Это меньше 5%. Коэффициент 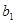 статистически значим. статистически значим.
Получили линейную модель  . .
Проверим модель на адекватность. Проанализировав таблицу дисперсионный анализ можно сказать, разброс данных, объясняемый регрессией  . Остатки, необъясненный разброс . Остатки, необъясненный разброс  . Общий разброс данных . Общий разброс данных  . Коэффициент детерминации . Коэффициент детерминации  . Разброс данных объясняется на 59,92% линейной моделью и на 40,08% - случайными ошибками. . Разброс данных объясняется на 59,92% линейной моделью и на 40,08% - случайными ошибками.
Проверим модель с помощью критерия Фишера. Для проверки найдем величины:  и и  . Вычисляем . Вычисляем  и и  . Находим наблюдаемое значение критерия Фишера . Находим наблюдаемое значение критерия Фишера  . Значимость этого критерия . Значимость этого критерия  , т.е. процент ошибки практически равен 0%, что меньше чем 5%. Модель , т.е. процент ошибки практически равен 0%, что меньше чем 5%. Модель  считается адекватной с гарантией более 95%. Так как линейная модель адекватна, то и соответствующая ей нелинейная модель адекватна. Находим параметры исходной нелинейной модели: считается адекватной с гарантией более 95%. Так как линейная модель адекватна, то и соответствующая ей нелинейная модель адекватна. Находим параметры исходной нелинейной модели: 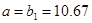 ; ; 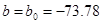 . .
Вид нелинейной функции:  . Таким образом, можно сказать, что зависимость уровня рентабельности от производительности труда можно описать следующей функцией: . Таким образом, можно сказать, что зависимость уровня рентабельности от производительности труда можно описать следующей функцией:  . .
Найдем прогноз. Примем за точку прогноза значение производительности труда 2500 грн.
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза: .
 . .
Построим доверительную область для точки прогноза и всех точек.
Найдем полуширину доверительного интервала в каждой точке выборки:
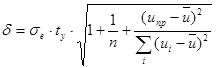 , ,
где 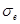 - среднеквадратическое отклонение выборочных точек от линии регрессии; - среднеквадратическое отклонение выборочных точек от линии регрессии; 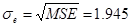 ; ;
 ‑ критическая точка распределения Стьюдента для надежности ‑ критическая точка распределения Стьюдента для надежности  и и  ; ; 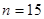 . .
Прогнозируемый доверительный интервал для любого x такой  , где , где  , т.е. доверительный интервал для , т.е. доверительный интервал для  составит от 5,35 до 14,03 с гарантией 95%., т.е. при производительности 2500 грн. Уровень рентабельности составит от 5,35% до 14,03%. составит от 5,35 до 14,03 с гарантией 95%., т.е. при производительности 2500 грн. Уровень рентабельности составит от 5,35% до 14,03%.
Для нелинейной модели найдем доверительный интервал, воспользовавшись обратной заменой: 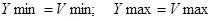 . Совокупность доверительных интервалов для всех X из области прогнозов образует доверительную область. . Совокупность доверительных интервалов для всех X из области прогнозов образует доверительную область.
Найдем эластичность.
Для линейной модели  тогда тогда  . .
Коэффициент эластичности для точки прогноза: 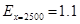
Коэффициент эластичности показывает, что при увеличении производительности на 1% уровень рентабельности увеличится с 9,69% на 1.1%. Т.е. при увеличении производительности труда рентабельность растет.
Задание № 3.3
Обозначим Фондоотдачу (грн.) – Х1, Производительность труда в расчете на одного работника (грн) – X2, Уровень рентабельности (%) – Y. Построим линейную зависимость показателя от факторов.
Прежде чем строить модель проверим факторы на коллинеарность. По исходным данным строим корреляционную матрицу. Коэффициент корреляции между X1 и X2 равен 0,87. Так как  , значит X1 и X2 – неколлинеарные факторы. Пытаемся описать связь между X и Y зависимостью , значит X1 и X2 – неколлинеарные факторы. Пытаемся описать связь между X и Y зависимостью  . .
Параметры  находим по методу наименьших квадратов. находим по методу наименьших квадратов.
 . .
Проверим значимость коэффициентов  . .
Значимость коэффициента может быть проверена с помощью критерия Стьюдента:
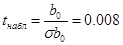 . .
Значимость  равна 0,99, т.е 99% больше 5%. Коэффициент равна 0,99, т.е 99% больше 5%. Коэффициент  статистически незначим. статистически незначим.
 . .
Значимость  равна равна 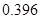 , т.е. 39,6%, что больше 5%. Коэффициент , т.е. 39,6%, что больше 5%. Коэффициент  статистически незначим. статистически незначим.
 . .
Значимость  равна равна  , т.е. 35%, что больше 5%. Коэффициент , т.е. 35%, что больше 5%. Коэффициент  статистически незначим. статистически незначим.
Проверим модель на адекватность.
Проанализировав таблицу дисперсионный анализ можно сказать, разброс данных, объясняемый регрессией  . Остатки, необъясненный разброс . Остатки, необъясненный разброс  . Общий разброс данных . Общий разброс данных  . Коэффициент детерминации . Коэффициент детерминации  . Разброс данных объясняется на 54,11% линейной моделью и на 45,89% - случайными ошибками. . Разброс данных объясняется на 54,11% линейной моделью и на 45,89% - случайными ошибками.
Проверим модель с помощью критерия Фишера. Для проверки найдем величины: 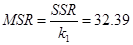 и и  . Вычисляем . Вычисляем 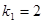 и и  . Находим наблюдаемое значение критерия Фишера . Находим наблюдаемое значение критерия Фишера  . Значимость этого критерия . Значимость этого критерия  , т.е. процент ошибки практически равен 0%, что меньше чем 5%. , т.е. процент ошибки практически равен 0%, что меньше чем 5%.
Модель считается адекватной с гарантией более 95%.
Из полученной модели можно сделать вывод, что уровень рентабельности от фондоотдачи и производительности труда описывается следующей зависимостью: 
Найдем прогноз.
Примем за точку прогноза значение производительности труда 25000 грн, фондоотдачи 33 грн. Получили при данных условиях уровень рентабельности
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза:
 . .
Найдем эластичность по каждому фактору.
Для линейной модели  , т.е. при производительности труда 2500 грн. и увеличении фондоотдачи с 33 грн. на 1% уровень рентабельности снижается на 0,4736%. , т.е. при производительности труда 2500 грн. и увеличении фондоотдачи с 33 грн. на 1% уровень рентабельности снижается на 0,4736%.
 , т.е. при фондоотдаче 33 грн и увеличении производительности труда с 2500 грн. на 1% уровень рентабельности увеличивается на 0,5243%. , т.е. при фондоотдаче 33 грн и увеличении производительности труда с 2500 грн. на 1% уровень рентабельности увеличивается на 0,5243%.
Значит для увеличения рентабельности целесообразнее увеличивать производительность труда.
|