| Введение
Актуальность темы. На данный момент эта тема очень актуальна, т.к. успешная реализация достижений научно – технического прогресса в нашей стране тесным образом связана с использованием математических методов и средств вычислительной техники при решении задач из различных областей человеческой деятельности. Исключительно важное значение приобретает использование указанных методов и средств при решении экономических задач. В связи с этим для студентов экономических специальностей вузов необходимо как знание возможностей применения математических методов, так и понимание тех проблем, которые возникают при их использовании.
Цель курсовой работы - изучить методы решения задач линейного программирования и научиться применять на практике решение задачи графическим, симплекс-методом (аналитическим и табличным) для прямой и двойственной задачи линейного программирования, а также научиться решать транспортную задачу.
Задачи работы:
изучить литературу по данной теме
для заданного варианта получить решение задачи линейного программирования:
- графическим методом;
- симплекс - методом для прямой задачи;
- симплекс - методом для двойственной задачи.
- сформулировать двойственную задачу и найти её решение.
- сформулировать и решить транспортную задачу.
Результаты работы рекомендуется использовать для успешного решения задач линейного программирования и дальнейшего изучения математического и линейного программирования.
Задачи математического и линейного программирования
Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения.
При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих соотношениях выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.п.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование», или «математические методы исследования операций».
Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование.
Сюда же обычно относят стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.
Математическое программирование — это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные.
Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразовании, транспортные задачи и т.п.
Построение математической модели экономической задачи включает следующие этапы:
1) выбор переменных задачи;
2) составление системы ограничений;
3) выбор целевой функции.
Переменными задачи называются величины x1 , x2 , ..., хп , которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора Х= (х1, х2, ..., хп).
Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например положительности переменных и т.п.
Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.
Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования.
Допустимым решением (планом) задачи линейного программирования (ЗЛП) называется любой n-мерный вектор Х= (х1, х2, ..., хn), удовлетворяющий системе ограничений и условиям неотрицательности.
Множество допустимых решений (планов) задачи образует область допустимых решений (ОДР).
Оптимальным решением (планом) ЗЛП называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.
Общий вид задачи линейного программирования:

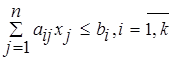


 , ,
Ограничения:
1. Правые части всех ограничений должны быть неотрицательными  . Если какой-нибудь из коэффициентов . Если какой-нибудь из коэффициентов  < 0, то необходимо коэффициенты ограничения слева и справа домножить на "-1" и изменить знак данного ограничения на противоположный; < 0, то необходимо коэффициенты ограничения слева и справа домножить на "-1" и изменить знак данного ограничения на противоположный;
2. Все ограничения должны быть представлены в виде равенств, поэтому при переходе от неравенства к равенству используют аппарат дополнительных переменных.
Если исходные ограничения определяют расход некоторого ресурса (знак " "), то переменные "), то переменные
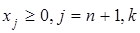
следует интерпретировать как остаток, или неиспользованную часть ресурса. В этом случае  – остаточная переменная и вводится в уравнение со знаком "+". Если исходные ограничения определяют избыток некоторого ресурса (знак " – остаточная переменная и вводится в уравнение со знаком "+". Если исходные ограничения определяют избыток некоторого ресурса (знак "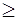 "), то вводится избыточная переменная "), то вводится избыточная переменная
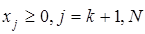
знаком "-".
Переменные:
Все переменные должны быть неотрицательными, т.е.
 . .
Если переменная не имеет ограничения в знаке, то её нужно представить как разность двух неотрицательных переменных:
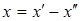 , ,
где 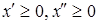 . Такую подстановку следует использовать во всех ограничениях, содержащих эту переменную, а также в выражении для целевой функции. . Такую подстановку следует использовать во всех ограничениях, содержащих эту переменную, а также в выражении для целевой функции.
Если такая переменная попадает в оптимальное решение, то  . .
Целевая функция:
Целевая функция задачи линейного программирования есть уравнение плоскости (или гиперплоскости для числа переменных больше трех). Максимальное или минимальное значение целевая функция задачи линейного программирования достигает либо в вершине выпуклого многогранника, либо на одной из его граней. Таким образом, решение (решения) задачи линейного программирования лежит в вершинах выпуклого многогранника и для его нахождения надо вычислить значения целевой функции в вершинах выпуклого многогранника, определяемого условиями-ограничениями задачи.
Приступаем к решению задачи.
Требуется составить план производства изделий А₁ и А₂ обеспечивающий максимальную прибыль предприятия от реализации готовой продукции. Необходимо:
Решить задачу геометрически;
Решить задачу симплекс-методом(аналитическим и табличным)
Сформулировать двойственную задачу и найти её решение.
Задача №1
Предприятие предполагает выпускать два вида продукции А₁ и А₂, для производства которых используется сырьё трех видов. Производство обеспечено сырьем каждого вида в количествах: b₁, b₂, b₃ кг. На изготовление единицы изделия А₁ требуется затратить сырья каждого вида а₁₁, а₂₁, а₃₁ кг, соответственно, а для единицы изделия А₂ - а₁₂, а₂₂, а₃₂ кг. Прибыль от реализации единицы изделия А₁ составляет с₁ ден.ед., для единицы изделия А₂ - с₂ ден.ед.
Вспомогательная таблица
| Вид сырья
|
Продукция
|
Ограничения по сырью
|
| А₁
|
А₂
|
| 1-й
|
а₁₁
|
а₁₂
|
b₁
|
| 2-й
|
а₂₁
|
а₂₂
|
b₂
|
| 3-й
|
а₃₁
|
а₃₂
|
b₃
|
| прибыль
|
с₁
|
с₂
|
Решение задачи геометрическим методом
Трудность построения математической модели заключается в идентификации переменных и последующем представлении цели и ограничений в виде математических функций этих переменных. Если модель содержит только две переменные, то задачу линейного программирования можно решить графически. В случае трёх переменных графическое решение становится менее наглядным, а при большем значении переменных – даже невозможным. Однако графическое решение позволяет сделать выводы, которые служат основой для разработки общего метода решения задачи линейного программирования.
Первый шаг при использовании графического метода заключается в геометрическом представлении допустимых решений, т.е. построении области допустимых решений (ОДР.), в которой одновременно удовлетворяются все ограничения модели. При получении графического решения переменная X1 откладывается по горизонтальной оси, а X2 – по вертикальной. При формировании ОДР необходимо предотвратить получение недопустимых решений, которые связаны с необходимостью выполнения условия неотрицательности переменных. Перед построением необходимо определить квадранты, в которых будет располагаться ОДР. Квадранты определяются знаками переменных X1 и X2. Условия неотрицательности переменных X1 и X2 ограничивают область их допустимых значений первым квадрантом. Если переменная X1 не ограниченна в знаке, то область ограничивается первым и вторым квадрантом, если X2, то – первым и четвёртым квадрантом.
Области, в которых выполняются соответствующие ограничения в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных.
В результате построений получается многоугольник, который определяет пространство решений. Если одно из ограничений имеет знак "=", то ОДР вырождается в отрезок.
В каждой точке, принадлежащей области или границам многоугольника решений, все ограничения выполняются, поэтому все решения, соответствующие этим точкам, являются допустимыми. Пространство решений содержит бесконечное число таких точек, несмотря на это, можно найти оптимальное решение. Для этого необходимо построить в плоскости переменных X1, X2 градиент целевой функции. Определение оптимальной точки зависит от той задачи, которую необходимо решить.
Если в целевой функции определена задача максимизации, то оптимальная точка будет располагаться в направлении увеличения градиента, если задача минимизации – то в направлении уменьшения градиента целевой функции. Для определения оптимальной точки будем перемещать целевую функцию в направлении увеличения (уменьшения) градиента до тех пор, пока она не сместиться в область недопустимых решений.
После нахождения оптимальной точки пространства решений определяют её координаты X1 *, X2 *и значение целевой функции F * в ней. Правильность выбора оптимальной точки можно проверить расчётом целевой функции в вершинах многогранника решений. В ЗЛП область допустимых решений всегда является выпуклым множеством, т.е. таким множеством, что наряду с любыми двумя точками, принадлежащими этому множеству, этому же множеству принадлежит и отрезок, соединяющий эти две точки. Любая функция наискорейшим образом увеличивается в направлении своего градиента.
Далее приступаем к решению задачи:
Занесём необходимые нам данные во вспомогательную таблицу:
| Вид сырья
|
Продукция
|
Ограничения по сырью
|
| А₁
|
А₂
|
| 1-й
|
5
|
2
|
750
|
| 2-й
|
4
|
5
|
807
|
| 3-й
|
1
|
7
|
840
|
| прибыль
|
30
|
49
|
Решение:
Предположим, что будет изготовлено Х₁ единиц изделий вида А₁ и Х₂ единиц - вида А₂. Поскольку производство продукции ограничено имеющимися в распоряжении предприятия сырьем каждого вида и количество изготовляемых изделий не может быть отрицательным, должны выполняться неравенства:
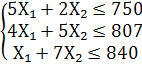
Общая прибыль от реализации Х₁ изделий А₁ и Х₂ изделий вида А₂ составит
F = 30Х₁ +49Х₂ . .
Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение.
Найдем решение сформулированной задачи, используя ее геометрическую интерпретацию. Сначала определим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств и найдем соответствующие прямые:

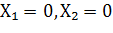
Эти прямые изображены на рис №1. Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой — нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли ее координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае — другая полуплоскость.
Найдем, например, полуплоскость, определяемую неравенствами.

Построим область допустимых решений:
для прямой

С(0;0) => 5·0+2·0=0, а 0≤750, значит прямая стремится к нулю (рис.1)
для прямой 

В(0;0) => 4·0+5·0=0, а 0≤807, значит прямая стремится к нулю (рис.1)
для прямой 

А(0;0) => 1·0+7·0=0, а 0≤840, значит прямая стремится к нулю (рис.1). Это и показано стрелками.
Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи.
Как видно из рис №1, многоугольником решений является пятиугольник OABCD. Координаты любой точки, принадлежащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику OABCD, в которой функция F принимает максимальное значение.
Чтобы найти указанную точку, построим вектор ñ =(30; 49) и прямую 30Х1 + 49Х2 = h, где h — некоторая постоянная такая, что прямая 30Х1 + 49Х2 = h имеет общие точки с многоугольником решений. Положим, например, h = 510 и построим прямую 30Х1 + 49Х2 = 510 (рис. №1).
Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то ее координаты определяют такой план производства изделий А1 и А2, при котором прибыль от их реализации равна 510 руб. Далее, полагая h равным некоторому числу, большему чем 510, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки определяют планы производства изделий А1 и А2, при которых прибыль от их реализации превзойдет 510 руб.
Перемещая построенную прямую 30Х1 + 49Х2 = 510 в направлении вектора ñ, видим, что последней общей точкой ее с многоугольником решений задачи служит точка В. Координаты этой точки и определяют план выпуска изделий А1 и А2, при котором прибыль от их реализации является максимальной.
Найдем координаты точки В как точки пересечения прямых  и и  . Следовательно, ее координаты удовлетворяют уравнениям этих прямых . Следовательно, ее координаты удовлетворяют уравнениям этих прямых
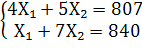
Решим эту систему уравнений:
Х1 = 840 – 7Х2, подставим полученное в первое уравнение  => 3360 – 28Х2 + 5Х2 = 807 => 23Х2 = 2553 => => 3360 – 28Х2 + 5Х2 = 807 => 23Х2 = 2553 =>
Х2 = 111, из этого решения следует, что Х1 = 840 – 7·111 = 63 => Х1 = 63
Следовательно, если предприятие изготовит 63 изделий вида А1 и 111 изделий вида А2, то оно получит максимальную прибыль, равную Fmax = 30·63 + 49·111= 7329 руб.
Решение задачи аналитическим симплекс-методом
Симплексный метод — это метод целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов расчета либо найти оптимальное решение, либо установить, что оптимального решения не существует.
Идея симплексного метода состоит в следующем. Используя систему ограничений, приведенную к общему виду, т. е. к системе т линейных уравнений с п переменными (т < п), находят ее любое базисное решение, по возможности наиболее простое. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то переходят к другому допустимому базисному решению.
Симплексный метод гарантирует, что при этом новом решении линейная форма если и не достигнет оптимума, то приблизится к нему (в случае перехода к вырожденному базисному решению значение линейной формы не изменится). С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным.
Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляют переход к другим базисным решениям, которые позволяют приблизиться к области допустимых решений, пока на каком-то шаге не получится допустимое выше.
Дадим математическую формулировку задачи. Пусть Х1 и Х2 — количество изделий А1 и А2, запланированных к производству. Так как количество сырья по каждому виду ограничено, то должны выполняться следующие неравенства:
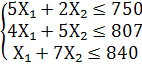

Эта система неравенств и является системой ограничений данной задачи. Целевая функция (линейная форма), выражающая прибыль предприятия, имеет вид
F = 30Х₁ +49Х₂ . .
Итак, задача сводится к нахождению максимума функции F = 30Х₁ +49Х₂ при ограничениях:
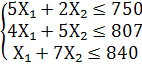

Для сведения системы ограничений-неравенств к системе уравнений прибавим к левой части каждого неравенства добавочные неотрицательные переменные Х3, Х4, Х5. В условиях данной задачи они имеют конкретное экономическое содержание, а именно выражают объем остатков сырья каждого вида после выполнения плана по выпуску продукции. После введения добавочных переменных получим систему уравнений:
5Х1+2Х2+Х3 = 750
4Х1+5 Х2+ Х4 = 807
Х1+7Х2+Х5 = 840
Хi≥0, i=1….5
Нужно найти такое допустимое базисное решение этой системы ограничений, которое бы максимизировало линейную форму F = 30Х₁ +49Х₂.
Так как система ограничений есть система трех независимых уравнений с двумя переменными, то число базисных переменных должно равняться трём, а число свободных - двум.
Для решения задачи симплексным методом прежде всего нужно найти любое базисное решение. В данном случае это легко сделать. Для этого достаточно взять в качестве базисных добавочные переменные Х3, Х4, Х5. Так как коэффициенты при этих переменных образуют единичную матрицу, то отпадает необходимость вычислять определитель. Считая свободными переменные Х1 и Х2 равными нулю, получим базисное решение (0; 0; 750; 807; 840), которое к тому же оказалось допустимым. Переходим к поискам оптимального решения.
I ш а г. Базисные переменные: Х3, Х4, Х5; свободные переменные: Х1 и Х2. В системе (1.1) базисные переменные выразим через свободные. Для того чтобы судить, оставить ли свободные переменные в числе свободных или их выгоднее с точки зрения приближения к оптимальному решению перевести в базисные, следует выразить через них и линейную форму (в данном случае она уже выражена через переменные Х1 и Х2). Тогда получим:
 Х3 = 750 - 5 Х1 - 2 Х2 Х3 = 750 - 5 Х1 - 2 Х2
Х4 = 807 - 4 Х1 - 5Х2
[Х5 = 840 - Х1 - 7Х2]
F = 30Х₁ +49Х₂
При Х1 = Х2 = 0 имеем Х3 = 750, Х4 = 807, Х5 = 840, что дает базисное решение (0; 0; 750; 807; 840), которое мы приняли за исходное. При этом базисном решении значение линейной формы
F = 30Х₁ +49Х₂ = 0.
Когда мы предположили, что Х1 = Х2 = 0 (предприятие ничего не выпускает), была поставлена цель — найти первое, безразлично какое, базисное решение. Эта цель достигнута. Теперь от этого первоначального решения нужно перейти к другому, при котором значение линейной формы увеличится. Из рассмотрения линейной формы видно, что ее значение возрастает при увеличении значений переменных Х1 и Х2. Иными словами, эти переменные невыгодно считать свободными, т. е. равными нулю, их нужно перевести в число базисных. Это и означает переход к новому базисному решению. При симплексном методе на каждом шаге решения предполагается перевод в число базисных только одной из свободных переменных. Переведем в число базисных переменную Х2 так как она входит в выражение линейной формы F = 30Х₁ +49Х₂ с большим коэффициентом.
Как только одна из свободных переменных переходит в число базисных, одна из базисных должна быть переведена на ее место в число свободных. Какую же из четырех базисных переменных нужно вывести? Ответить на этот вопрос помогут следующие рассуждения: значение Х2 необходимо сделать как можно большим, так как это соответствует конечной цели — максимизации F. Однако оказывается, что увеличение Х2 может продолжаться только до известных границ, а именно до тех пор, пока не нарушится требование неотрицательности переменных.
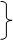  Х2 = min Х2 = min   ; ; = min{375; 161,4; 120} = 120, = min{375; 161,4; 120} = 120,
далее Х2 переведём в базисные вместо Х5.
II ш а г. Базисные переменные: Х3, Х4, Х2; свободные переменные: Х1, Х5. Выразим базисные переменные и линейную форму через свободные. В системе (1.2) берем то уравнение, из которого получено минимальное значение отношения свободного члена к коэффициенту при Х2. В данном случае это третье уравнение, которое выделено рамкой. Выразив из этого уравнения Х2, получим:
Х2 = 120 -  Х1 - Х1 -  Х5 Х5
Подставив это выражение Х2 во все остальные уравнения системы (1.2) и в линейную форму F, получим:
 Х2 = 120 - Х2 = 120 -  Х1 - Х1 -  Х5 Х5
Х3 = 750 - 5 Х1 – 2(120 -  Х1 - Х1 -  Х5) = 510 - Х5) = 510 -  Х1 + Х1 +  Х5 Х5
Х4 = 807 - 4 Х1 – 5(120 -  Х1 - Х1 -  Х5) = 207 - Х5) = 207 -  Х1 + Х1 + 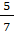 Х5 Х5
 Х2 = 120 - Х2 = 120 -  Х1 - Х1 -  Х5 Х5
Х3 = 510 -  Х1 + Х1 +  Х5 Х5 [Х4 = 207 -  Х1 + Х1 +  Х5] Х5]
F = 30Х₁ +49(120 -  Х1 - Х1 -  Х5) = 5880 + 23 Х1 - 7 Х5 Х5) = 5880 + 23 Х1 - 7 Х5
При Х1 = Х5 = 0 имеем F = 5880. Это уже лучше, чем на I шаге, но не искомый максимум. Дальнейшее увеличение функции F возможно за счет введения переменной Х1 в число базисных; так как эта переменная входит в выражение F с положительным коэффициентом, поэтому ее увеличение приводит к увеличению линейной формы и ее невыгодно считать свободной, т. е. равной нулю.
  Для ответа на вопрос, какую переменную вывести из базисных в свободные, примем: Для ответа на вопрос, какую переменную вывести из базисных в свободные, примем:
Х1 = min   ; ;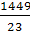 = min{840; 108,2; 63} = 63, = min{840; 108,2; 63} = 63,
далее Х1 переведём в базисные вместо Х4.
III шаг. Базисные переменные: Х1, Х2, Х3; свободные переменные: Х4, Х5. Выразим основные переменные и линейную форму через свободные. Из последнего уравнения системы (1.3) имеем:
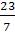 Х1 = 207 + Х1 = 207 +  Х5 – Х4 => Х1 = 63 + Х5 – Х4 => Х1 = 63 + 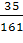 Х5 - Х5 -  Х4 Х4
Подставляя это выражение в остальные уравнения и в линейную форму, получим:
 Х1 = 63 + Х1 = 63 + 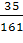 Х5 - Х5 -  Х4 Х4
Х2 = 120 -  (63 + (63 + 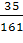 Х5 - Х5 -  Х4) - Х4) -  Х5 = 111 - Х5 = 111 - 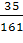 Х5 - Х5 - 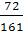 Х4 Х4
Х3 = 510 - 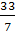 (63 + (63 + 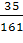 Х5 - Х5 -  Х4) + Х4) +  Х5 = 213 - Х5 = 213 -  Х5 + Х5 + 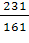 Х4 Х4
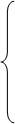 Х1 = 63 + Х1 = 63 + 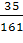 Х5 - Х5 -  Х4 Х4
Х2 = 111 - 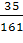 Х5 - Х5 - 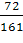 Х4 Х4 Х3 = 213 -  Х5 + Х5 + 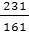 Х4 Х4
F = 5880 + 23(63 + 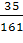 Х5 - Х5 -  Х4) - 7 Х5 = 7329 - 2 Х5 - 7 Х4 Х4) - 7 Х5 = 7329 - 2 Х5 - 7 Х4
Так как в выражение линейной формы переменные Х4 и Х5 входят с отрицательным коэффициентами, то никакое увеличение F за счет этих переменных невозможно.
Следовательно, на III шаге критерий оптимальности достигнут и задача решена. Оптимальным служит решение (63;111;213;207;0), при котором Fmаx= 7329.
Таким образом, для получения наибольшей прибыли, равной 7329 ден. ед., из данных запасов сырья предприятие должно изготовить 63 вида изделий А1 и 111изделий вида А2.
Ответ: Х1* = 63; Х2* = 111. Fmаx= 7329.
Решить задачу табличным симплексным методом
Рассмотренный симплексный метод решения ЗЛП в предыдущем пункте можно свести к записи однотипно заполняемых таблиц. Осуществить это возможно, придерживаясь следующего алгоритма:
Привести задачу линейного программирования к каноническому виду.
Найти начальное опорное решение с базисом из единичных векторов и коэффициенты разложений векторов условий по базису опорного решения. Если опорное решение отсутствует, то задача не имеет решения в силу несовместности системы ограничений.
Вычислить оценки разложений векторов условий по базису опорного решения и заполнить симплексную таблицу.
Если выполняется признак единственности оптимального решения (для любого вектора условий, не входящего в базис, оценка отлична от нуля), то решение задачи заканчивается.
Если выполняется условие существования множества оптимальных решений (оценка хотя бы одного вектора условий, не входящего в базис, равна нулю), то путем простого перебора находят все оптимальные решения.
Если выполняются условия отсутствия оптимального решения вследствие неограниченности целевой функции (не имеет решения, если для какого-либо из векторов условий с оценкой, противоречащей признаку оптимальности, среди коэффициентов разложения по базису опорного решения нет положительного), то задача не имеет решения ввиду неограниченности целевой функции.
Если пункты 4-6 алгоритма не выполняются, находят новое опорное решение с использованием условий нахождения оптимального решения.
Составим математическую модель задачи. Искомый выпуск продукции А1 обозначим через Х1, продукции А2 – Х2. Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида, переменные Х1, Х2 должны удовлетворять следующей системе неравенств:
 5Х1+2Х2 ≤ 750 5Х1+2Х2 ≤ 750
4Х1+5 Х2 ≤ 807 Х1+7Х2 ≤ 840
Х1≥0, Х2≥0
Общая стоимость произведенной предприятием продукции при условии выпуска Х1изделий А1 и Х2 изделий А2 составляет F = 30Х₁ +49Х₂
По своему экономическому содержанию переменные Х1 и Х2 могут принимать только лишь неотрицательные значения: Х1, Х2 ≥0.
Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы неравенств (1.1) требуется найти такое, при котором функция F = 30Х₁ +49Х₂ принимает максимальное значение.
Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений:
5Х1+2Х2+Х3 = 750
4Х1+5 Х2+ Х4 = 807 Х1+7Х2+Х5 = 840
Хi≥0, i=1….5
Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида. Например, Х3 — это неиспользуемое количество сырья 1-ого вида и т.д.
Для решения задачи табличным симплексным методом прежде всего нужно найти любое базисное решение. В данном случае это легко сделать. Для этого достаточно взять в качестве базисных добавочные переменные Х3, Х4, Х5.,а в качестве свободных переменные Х1 и Х2 равными нулю, получим базисное решение (0; 0; 750; 807; 840), которое к тому же оказалось допустимым. F = 30Х₁ +49Х₂ => F - 30Х₁ - 49Х₂ = 0
Переходим к поискам оптимального решения.
Составим симплексную таблицу:
Как видно из таблицы (2.1), значения всех переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение целевой функции равно нулю (т. е. стоимость произведенной продукции отсутствует). Этот план, конечно, не является оптимальным.
Это видно и из 4-й строки таблицы (2.1), так как в ней имеется два отрицательных числа: (- 30; - 49;0;0;0). Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции.
Даже с экономической точки зрения наиболее целесообразным является включение в план производства изделий А2. Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отрицательное число -49, стоит в 4-й строке 2-го столбца => этот столбец является разрешающим.Определяем вектор, подлежащий исключению из базиса и выбираем разрешающую строку. Для этого находим:
  Х2 = min Х2 = min  ; ;  ; ; = 120. = 120.
Найдя число 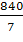 = 120, => 3-я строка (Х5) является разрешающей. Следовательно, в базис введем Х2 вместо Х5. Тем самым мы, с экономической точки зрения определили, какое количество изделий А2 предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида. = 120, => 3-я строка (Х5) является разрешающей. Следовательно, в базис введем Х2 вместо Х5. Тем самым мы, с экономической точки зрения определили, какое количество изделий А2 предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида.
Таблица (2.1)
| Базисные переменные
|
Свободные переменные
|
1
|
2
|
3
|
4
|
5
|
| Х1
|
Х2
|
Х3
|
Х4
|
Х5
|
| 1
|
Х3
|
750
|
5
|
2
|
1
|
0
|
0
|
| 2
|
Х4
|
807
|
 4 4
|
5
|
0
|
1
|
0
|
| 3
|
Х5
|
840
|
1
|
7
|
0
|
0
|
1
|
| 4
|
F
|
0
|
-30
|
-49
|
0
|
0
|
0
|
На пересечении разрешающего столбца и строки находится разрешающий элемент - это число 7. Производим пересчет всех коэффициентов таблицы, таким образом , чтоб на месте разрешающего элемента получить 1, а в разрешающем столбце все элементы = 0.
Для этого: 1) Третью строку разделим на 7, в результате получим на месте разрешающего элемента 1.
2) Третью строку умножим на 2 и из первой строки вычтем то, что получилось при умножении. Результат записываем в первую строку.
3) Третью строку домножим на 5 и из второй строки вычтем то, что получилось при умножении. Результат записываем во вторую строку.
4) Третью строку умножим на 49 и прибавим к строке F.
При пересчете у нас в столбике F, таблицы (2.2), опять оказалось отрицательное число, а это говорит о том что решение нужно продолжать.
Далее, разрешающим столбцом у нас будет Х1,т.к отрицательное число -23 находится в нем.
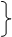 Определяем вектор, подлежащий исключению из базиса и выбираем разрешающую строку. Для этого находим: Определяем вектор, подлежащий исключению из базиса и выбираем разрешающую строку. Для этого находим:
 Х1 = min Х1 = min  ; ;  ; ; = 63. = 63.
Найдя число  = 63, => 2-я строка (Х4) является разрешающей. Следовательно, в базис введем Х1 вместо Х4. = 63, => 2-я строка (Х4) является разрешающей. Следовательно, в базис введем Х1 вместо Х4.
Запишем все расчёты в таблицу
Таблица (2.2)
| Базисные переменные
|
Свободные переменные
|
1
|
2
|
3
|
4
|
5
|
| Х1
|
Х2
|
Х3
|
Х4
|
Х5
|
| 1
|
Х3
|
510
|
 33/7 33/7
|
0
|
1
|
0
|
-2/7
|
| 2
|
Х4
|
207
|
23/7
|
0
|
0
|
1
|
-5/7
|
| 3
|
Х2
|
120
|
1/7
|
1
|
0
|
0
|
1/7
|
| 4
|
F
|
5880
|
-23
|
0
|
0
|
0
|
7
|
На пересечении разрешающего столбца и строки находится разрешающий элемент - это число 23/7. Производим пересчет всех коэффициентов таблицы, таким образом , чтоб на месте разрешающего элемента получить 1, а в разрешающем столбце все элементы = 0.
Для этого: 1) Третью строку разделим на  и запишем получившееся в эту же строку. и запишем получившееся в эту же строку.
2) Из первой строки вычтем вторую, умноженную на 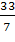 и записываем в первую строку. и записываем в первую строку.
3) Из третьей строки вычтем вторую умноженную на  , результат запишем в третью строку. , результат запишем в третью строку.
4) К строке F прибавим вторую строку умноженную на 23 и запишем в строку F.
Таблица (2.3)
| Базисные переменные
|
Свободные переменные
|
1
|
2
|
3
|
4
|
5
|
| Х1
|
Х2
|
Х3
|
Х4
|
Х5
|
| 1
|
Х3
|
213
|
0
|
0
|
1
|
-33/23
|
119/161
|
| 2
|
Х1
|
63
|
1
|
0
|
0
|
7/23
|
-5/23
|
| 3
|
Х2
|
111
|
0
|
1
|
0
|
-1/23
|
28/161
|
| 4
|
F
|
7329
|
0
|
0
|
0
|
7
|
2
|
Ответ: из изложенного выше экономического содержания данных таблицы (2.3) следует, что на втором шаге план задачи является оптимальным. Х1* = 63; Х2* = 111. Fmаx= 7329, это значит, что общая стоимость всей произведенной продукции, а она равна 7329 рублей, является максимальной
Решение задачи двойственным методом
Под двойственной задачей понимается вспомогательная задача линейного программирования, формулируемая с помощью определённых правил непосредственно из условий прямой задачи. Заинтересованность в определении оптимального решения прямой задачи путём решения двойственной к ней задачи обусловлена тем, что вычисления при решении ДЗ могут оказаться менее сложными. Трудоёмкость вычислений при решении ЗЛП в большей степени зависит от числа ограничений, а не от количества переменных.
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу линейного программирования, называемую двойственной или сопряженной по отношению к исходной или прямой.
 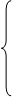 5Х1+2Х2 ≤ 750 Y1 5Х1+2Х2 ≤ 750 Y1
4Х1+5 Х2 ≤ 807 Y2 Х1+7Х2 ≤ 840 Y3
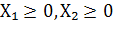
F = 30Х₁ +49Х₂ => max
Целевая функция исходной задачи задаётся на максимум, а целевая функция двойственной – на минимум.
  Составим матрицу для исходной задачи: Составим матрицу для исходной задачи:
А = 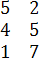
Чтобы составить матрицу для двойственной задачи нужно применить транспонирование (т.е. замена строк – столбцами, а столбцов – стоками)
  АТ = АТ = 
Число переменных в двойственной задаче равно числу соотношений в системе (1.1) исходной задачи, т.е. равно трем.
Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений, т .е 750,807,840.
Целевая функция исходной задачи исследуется на максимум, а система условий содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а её переменные могут принимать любые значения (в том числе и отрицательные). Следовательно, для исходной задачи двойственная задача такова: умножим правые части ограничений на соответствующие переменные двойственной задачи и сложим их, получим целевую функции
Z(Y) = 750Y1 + 807Y2 + 840Y3 => min.
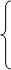 5Y1 + 4Y2 + Y3 ≥ 30 5Y1 + 4Y2 + Y3 ≥ 30
2Y1 + 5Y2 + 7Y3 ≥ 49
Y1 = 0
Y2 = 7
Y3 = 2
Z(Y) = 750·0 + 807·7+ 840·2 = 7329
Ответ: Z(Y) = F(Х) = 7329, Y1* = 0, Y2* = 7, Y3* = 2.
Транспортная задача линейного программирования
Под названием «транспортная задача» объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
Задача №2
Формулировка транспортной задачи
На три базы: А₁, А₂, А₃ поступил однородный груз в количествах: а₁, а₂, а₃, соответственно. Груз требуется перевезти в пять пунктов: b₁ в пункт В₁, b₂ в пункт В₂, b₃ в пункт В₃, b₄ в пункт В₄, b₅ в пункт В₅.
Спланировать перевозки так, чтобы общая их стоимость была минимальной. Матрица тарифов сij перевозок между пунктами отправления и пунктами назначения, а также запасы и потребности представлены ниже:
| Пункт отправления
|
В₁
|
В₂
|
В₃
|
В₄
|
В₅
|
Запасы, аi
|
| А₁
|
2
|
4
|
5
|
11
|
3
|
400
|
| А₂
|
12
|
8
|
6
|
14
|
11
|
370
|
| А₃
|
10
|
15
|
7
|
9
|
18
|
380
|
| Потребности, bj
|
250
|
200
|
290
|
260
|
150
|
1150
|
Исходные данные транспортной задачи обычно записываются в таблице:
Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения. Проверяем выполнение необходимого и достаточного условия разрешимости задачи. Находим суммарные запасы поставщиков и запросы потребителей:  400 + 370 + 380 = 1150, 400 + 370 + 380 = 1150, 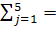 250 + 200 + 290 + 260 + 150 = 1150. => задача с правильным балансом. Составляем начальное опорное решение: 250 + 200 + 290 + 260 + 150 = 1150. => задача с правильным балансом. Составляем начальное опорное решение:
Таблица (1;1)
| 250
|
200
|
290
|
260
|
150
|
| V1
|
V2
|
V3
|
V4
|
V5
|
| 400
|
U1
|
2502
|
04
|
5
|
11
|
150 3
|
| 370
|
U2
|
12
|
 
808 |

2906 |
14
|
11
|
| 380
|
U3
|
10
|

120 15 |
*7 |
2609
|
18
|
Т.к. n + m – 1 = 3 + 5 – 1 = 7, а в нашей задаче заполненных клеток всего 6, введём дополнительное число - нуль, на пересечении U1 и V2.
 Получаем решение: Получаем решение:
 X1 = X1 = 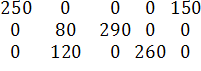 - опорное решение №1. - опорное решение №1.
Вычисляем значение целевой функции на этом опорном решении F = 250·2+ 150·3 + 80·8 + 290·6 + 120·15 + 260·9 = 500 + 450 + 640 + 1740 + 1800 + 2340 = 7470.
Для проверки оптимальности опорного решения необходимо найти потенциалы и оценки. По признаку оптимальности в каждой занятой опорным решением клетке таблицы транспортной задачи сумма потенциалов равна стоимости
Ui + Vj = Сij
Записываем систему уравнений для нахождения потенциалов:
 U1 + V1 = 2, U1 + V1 = 2,
U1 + V2 = 4,
U1 + V5 = 3,
U2 + V2 = 8,
U2 + V3 = 6,
U3 + V2 = 15,
U3 + V4 = 9
Далее одному из потенциалов задаем значение произвольно: пусть U1 = 0. Остальные потенциалы находятся однозначно:
 U1 = 0, U1 = 0,
V1 = 2, V2 = 4, V5 = 3
U2 = 8 - V2 = 4
U3 = 15 - V2 = 11
V4 = 9 - U3 = -2
V3 = 6 - U2 = 2
Проверяем опорное решение Х1 на оптимальность. С этой целью вычисляем оценки  для всех незаполненных клеток таблицы. для всех незаполненных клеток таблицы.
∆13 = U1 + V3 - С13 = 0 + 2 – 5 = - 3,
∆14 = U1 + V4 - С14 = 0 - 2 –11 = - 13,
∆21 = U2 + V1 – С21 = 4 + 2 – 12 = - 6,
∆24 = U2 + V4 – С24 = 4 - 2 – 14 = - 12,
∆25 = U2 + V5 – С25 = 4 + 3 – 11 = - 4,
∆31 = U3 + V1 – С31 = 11 + 2 – 10 = 3,
∆33 = U3 + V3 – С33 = 11 + 2 – 7 = 6,
∆35 = U3 + V5 – С35 = 11 + 3 – 18 = - 4.
Начальное опорное решение не является оптимальным, так как имеются положительные оценки.
Переходим к новому опорному решению. Находим клетку таблицы, которой соответствует наибольшая положительная оценка:
 max{3, 6}=6 - для клетки (U3; V3). max{3, 6}=6 - для клетки (U3; V3).
Для этой клетки строим цикл.
Циклом в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья – вдоль строк и столбцов, причём в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое – в столбце.
При правильном построении опорного плана для любой свободной клетки можно построить лишь один цикл. После того как для выбранной свободной клетки он построен, следует перейти к новому опорному плану. Для этого необходимо переместить грузы в пределах клеток, связанных с данной свободной клеткой.
Это перемещение производят по следующим правилам:
Каждой из клеток, связанных циклом с данной свободной клеткой приписывают определенный знак, причём свободной клетке – знак плюс, а всем остальным клеткам – поочередно знаки минус и плюс (таблица (1;1)).
В данную свободную клетку переносят меньшее из чисел, стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим клеткам, стоящим в плюсовых клетках, и вычитают из чисел, стоящих в минусовых клетках. Клетка, которая ранее была свободной, становится занятой, а минусовая клетка, в которой стояло минимальное из чисел, считается свободной (таблица (1;2)).
Описанный выше переход от одного опорного плана транспортной задачи к другому называется сдвигом по циклу пересчета.
| 250
|
200
|
290
|
260
|
150
|
| V1
|
V2
|
V3
|
V4
|
V5
|
| 400
|
U1
|
2502
|
04
|
5
|
11
|
150 3
|
| 370
|
U2
|
12
|
2008
|
1706
|
14
|
11
|
| 380
|
U3
|
10
|
15
|
1207
|
2609
|
18
|
  Следует отметить, что при сдвиге по циклу пересчета число занятых клеток остается неизменным, а именно остается равным n + m – 1 = 3 + 5 – 1 = 7 Следует отметить, что при сдвиге по циклу пересчета число занятых клеток остается неизменным, а именно остается равным n + m – 1 = 3 + 5 – 1 = 7
X2 =  - опорное решение №2. Полученный новый опорный план проверяем на оптимальность. - опорное решение №2. Полученный новый опорный план проверяем на оптимальность.
Вычисляем значение целевой функции на втором опорном решении:
F = 250· 2 + 0·4+ 150·3+ 200·8+ 170·6 + 120·7 + 260·9 = 500 + 0 + 450 + 1600 + 1020 + 840 + 2340 = 6750.
Далее производим проверку оптимальности опорного решения:
 U1 + V1 = 2, U1 + V1 = 2,
U1 + V2 = 4,
U1 + V5 = 3,
U2 + V2 = 8,
U2 + V3 = 6,
U3 + V4 = 9.
U1 = 0,
V1 = 2, V2 = 4, V5 = 3
U2 = 8 - V2 = 4
V3 = 6 - U2 = 2
U3 = 7 – V3 = 5
V4 = 9 - U3 = 4
Проверяем опорное решение Х2 на оптимальность. С этой целью вычисляем оценки  для всех незаполненных клеток таблицы. для всех незаполненных клеток таблицы.
∆13 = U1 + V3 - С13 = 0 + 2 – 5 = - 3,
∆14 = U1 + V4 - С14 = 0 + 4 –11 = - 7,
∆21 = U2 + V1 – С21 = 4 + 2 – 12 = - 6,
∆24 = U2 + V4 – С24 = 4 + 4 – 14 = - 6,
∆25 = U2 + V5 – С25 = 4 + 3 – 11 = - 4,
∆31 = U3 + V1 – С31 = 5 + 2 – 10 = - 3,
∆35 = U3 + V5 – С35 = 5 + 4 – 18 = - 9.
Ответ: общая минимальная стоимость перевозок равна F min = 6750ден.ед при решении
  Х2 = Х2 =  . .
Заключение
В результате проделанной работы изучено несколько методов решения задачи линейного программирования, а именно графический, симплекс-метод (аналитический и табличный) для прямой и двойственной задачи линейного программирования, а также изучена транспортная задача.
Для достижения поставленной цели были использованы различные источники литературы. На практике рассмотрено решение задачи заданными методами и решена транспортная задача.
Результаты работы рекомендуется использовать для успешного решения задач линейного программирования и дальнейшего изучения математического и линейного программирования.
Библиографический список
1. Абрамов Л.M., Капустин В.Ф. Математическое программирование. ―Л., 1981.
2. Акулич И.Л. Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986.
3. Баумоль У. Экономическая теория и исследование операций. — М.: Прогресс, 1965.
4. Калихман И.Л. Линейная алгебра и программирование. — М.: Высш. шк.,1967.
5. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. Ч.II. Теория вероятностей и математическое программирование. Линейное программирование: Учеб. пособие для студентов вузов. ― М.: Высш. школа, 1982.
6. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. ― М.: Высш. шк., 1980.
7. Линейное программирование: Учебно-методическое пособие. ― М.: Изд-во МГУ, 1992.
8. Матвеев В.И., Сагитов Р.В., Шершнев В.Г. Курс линейного программирования для экономистов: Учеб. пособие. — М.: Менеджер, 1998.
9. Муртаф Б. Современное линейное программирование. — М.: Мир, 1984.
10. Общий курс высшей математики для экономистов :Учебник / Под ред. В.И. Ермакова. ― М.: ИНФА-М, 2002.
|