1) Выберем переменными задачи x1
– изделий вида А1
; x2
– изделий вида А2
.
Составим систему ограничений в виде неравенств
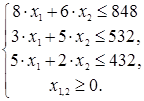
Составим целевую функцию z
(x)
= 25·x1
+ 17·x2
→ max, т.е. обеспечить максимальную выручку от реализации готовой продукции.
2) Найдем решение сформулированной задачи, используя ее геометрическую интерпретацию. Сначала определим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств и найдем соответствующие прямые

Эти прямые изображены на рис. 1. Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи.

Рис. 1. Графическое представление математической модели
Как видно из рис. 1, многоугольником решений является пятиугольник ОАВС
D
. Координаты любой точки, принадлежащей данному пятиугольнику, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику ОАВС
D
, в которой функция z
принимает максимальное значение. Чтобы найти указанную точку, построим вектор 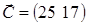 , перпендикулярный прямой 25·x1
+ 17·x2
= h
, где h
– некоторая постоянная такая, что данная прямая имеет общие точки с многоугольником решений. , перпендикулярный прямой 25·x1
+ 17·x2
= h
, где h
– некоторая постоянная такая, что данная прямая имеет общие точки с многоугольником решений.
Перемещая, данную прямую в направлении вектора 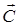 , видим, что последней общей точкой ее с многоугольником решений задачи служит точка B.
Координаты этой точки и определяют план производства продукции, при котором выручка от их реализации будет максимальной. , видим, что последней общей точкой ее с многоугольником решений задачи служит точка B.
Координаты этой точки и определяют план производства продукции, при котором выручка от их реализации будет максимальной.
Находим координаты точки C
как координаты точки пересечения прямых 8·x1
+ 6·x2
= 848 и 5·x1
+ 2·x2
= 432.
Решив эту систему уравнений, получим  , , 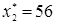 . Итак, выручка от реализации будет наибольшей, если в плане по производству содержится выпуск 64 изделий А1
и 56 изделий А2
, и, составляет 25·64 + 17·56 = 2552 ден. ед. . Итак, выручка от реализации будет наибольшей, если в плане по производству содержится выпуск 64 изделий А1
и 56 изделий А2
, и, составляет 25·64 + 17·56 = 2552 ден. ед.
3) Запишем данную задачу в форме основной задачи линейного программирования. Для этого от ограничений-неравенств перейдем к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений

Составляем таблицу первой итерации:
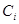 |
Базисные
переменные
|
25 |
17 |
0 |
0 |
0 |
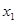 |
 |
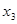 |
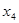 |
 |
0
0
0
|
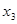
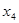

|
848
532
432
|
8
3
5
|
6
5
2
|
1
0
0
|
0
1
0
|
0
0
1
|
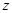 |
0 |
-25 |
-17 |
0 |
0 |
0 |
В 4-й строке табл. в столбцах переменных 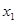 , ,  , имеются отрицательные числа. Наличие этих чисел говорит о том, что данный план не является оптимальным. Переходим к новому плану задачи: разрешающий элемент выделен (здесь и далее) подчеркиванием
. , имеются отрицательные числа. Наличие этих чисел говорит о том, что данный план не является оптимальным. Переходим к новому плану задачи: разрешающий элемент выделен (здесь и далее) подчеркиванием
.
Вторая итерация
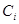 |
Базисные
переменные
|
25 |
17 |
0 |
0 |
0 |
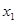 |
 |
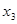 |
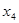 |
 |
0
0
25
|
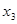
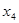
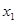
|
784/5
1364/5
432/5
|
0
0
1
|
14/5
19/5
2/5
|
1
0
0
|
0
1
0
|
-8/5
-3/5
1/5
|
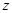 |
2160 |
0 |
-7 |
0 |
0 |
0 |
Третья итерация
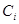 |
Базисные
переменные
|
25 |
17 |
0 |
0 |
0 |
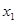 |
 |
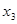 |
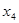 |
 |
17
0
25
|

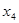
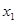
|
56
60
64
|
0
0
1
|
1
0
0
|
5/14
-19/14
-1/7
|
0
1
0
|
-4/7
11/7
3/7
|
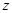 |
2552 |
0 |
0 |
5/2
|
0
|
1
|
Из табл. видно, что найденный новый опорный план исходной задачи X* = (64;56; 0; 60; 0) является оптимальным. При этом maxz
= 2552.
Итак, выручка от реализации будет наибольшей, если в плане по производству содержится выпуск 64 изделий А1
и 56 изделий А2
, и, составляет 2552 ден. ед.
4)Для данной задачи 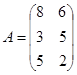 , тогда , тогда  . Число переменных в двойственной задаче равно числу уравнений в исходной задаче, т.е. 3. Коэффициенты в целевой функции двойственной задачи являются свободными членами неравенств-ограничений, т.е. числами 848, 532, 432. Т.к., в исходной системе ограничения представлены неравенствами, то в двойственной задаче переменные . Число переменных в двойственной задаче равно числу уравнений в исходной задаче, т.е. 3. Коэффициенты в целевой функции двойственной задачи являются свободными членами неравенств-ограничений, т.е. числами 848, 532, 432. Т.к., в исходной системе ограничения представлены неравенствами, то в двойственной задаче переменные  являются неотрицательными. являются неотрицательными.
Следовательно, двойственная задача такова: найти минимум функции z
*
(x)
= 848·y1
+ 532·y2
+ 432·y3
при условиях

Из последней симплекс-таблицы (итерация 3) видно, что двойственная задача имеет решение  , ,  , ,  . .
1) Распределительный метод
Примем некоторые обозначения: i
- индекс строки j
- индекс столбца m
- количество поставщиков n
- количество потребителей Xi,j
- перевозка между поставщиком Ai
и потребителем Bj
.
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Транспортная задача имеет закрытый тип, так как суммарный запас груза равен суммарным потребностям. Находим опорный план по правилу северо-западного угла: Введем некоторые обозначения: Ai
*
- излишек нераспределенного груза от поставщика Ai
Bj
*
- недостача в поставке груза потребителю Bj
Помещаем в клетку (1,1) меньшее из чисел A1
*
=370 и B1
*
=300 Так как спрос потребителя B1
удовлетворен, то столбец 1 в дальнейшем в расчет не принимается Помещаем в клетку (1,2) меньшее из чисел A1
*
=70 и B2
*
=280 Так как запасы поставщика A1
исчерпаны, то строка 1 в дальнейшем в расчет не принимается Помещаем в клетку (2,2) меньшее из чисел A2
*
=450 и B2
*
=210 Так как спрос потребителя B2
удовлетворен, то столбец 2 в дальнейшем в расчет не принимается Помещаем в клетку (2,3) меньшее из чисел A2
*
=240 и B3
*
=330 Так как запасы поставщика A2
исчерпаны, то строка 2 в дальнейшем в расчет не принимается Помещаем в клетку (3,3) меньшее из чисел A3
*
=480 и B3
*
=90 Так как спрос потребителя B3
удовлетворен, то столбец 3 в дальнейшем в расчет не принимается Помещаем в клетку (3,4) меньшее из чисел A3
*
=390 и B4
*
=290 Так как спрос потребителя B4
удовлетворен, то столбец 4 в дальнейшем в расчет не принимается Помещаем в клетку (3,5) меньшее из чисел A3
*
=100 и B5
*
=100
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F=11320
Решаем задачу распределительным методом:
Этап 1
Определим значения оценок Si,j
для всех свободных клеток (неоптимальные выделены красным цветом
). Для этого строим цикл для каждой свободной клетки и, перемещаясь по клеткам цикла, складываем тарифы клеток. При этом тарифы в нечетных клетках берутся со знаком "плюс", в четных - со знаком "минус". S1,3
= c1,3
-c1,2
+c2,2
-c2,3
= 12 S1,4
= c1,4
-c1,2
+c2,2
-c2,3
+c3,3
-c3,4
= 4 S1,5
= c1,5
-c1,2
+c2,2
-c2,3
+c3,3
-c3,5
= -3
S2,1
= c2,1
-c2,2
+c1,2
-c1,1
= 5 S2,4
= c2,4
-c2,3
+c3,3
-c3,4
= 8 S2,5
= c2,5
-c2,3
+c3,3
-c3,5
= -2
S3,1
= c3,1
-c3,3
+c2,3
-c2,2
+c1,2
-c1,1
= -14
S3,2
= c3,2
-c3,3
+c2,3
-c2,2
= -6
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
12 |
4 |
-3 |
| A2
|
5 |
8 |
-2 |
| A3
|
-14 |
-6 |
Если имеется несколько клеток с одним и тем же наименьшим значением оценки, то из них выбирается клетка, имеющая наименьший тариф. Наиболее перспективной является клетка (3,1)
. Для нее оценка равна -14
. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Перемещаем по циклу груз величиной в 90 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 10060
Значение целевой функции изменилось на 1260 единиц по сравнению с предыдущим этапом.
Этап 2
Определим значения оценок Si,j
для всех свободных клеток (неоптимальные выделены красным цветом
). Для этого строим цикл для каждой свободной клетки и, перемещаясь по клеткам цикла, складываем тарифы клеток. При этом тарифы в нечетных клетках берутся со знаком "плюс", в четных - со знаком "минус". S1,3
= c1,3
-c1,2
+c2,2
-c2,3
= 12 S1,4
= c1,4
-c1,1
+c3,1
-c3,4
= -10
S1,5
= c1,5
-c1,1
+c3,1
-c3,5
= -17
S2,1
= c2,1
-c2,2
+c1,2
-c1,1
= 5 S2,4
= c2,4
-c2,2
+c1,2
-c1,1
+c3,1
-c3,4
= -6
S2,5
= c2,5
-c2,2
+c1,2
-c1,1
+c3,1
-c3,5
= -16
S3,2
= c3,2
-c3,1
+c1,1
-c1,2
= 8 S3,3
= c3,3
-c3,1
+c1,1
-c1,2
+c2,2
-c2,3
= 14
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
12 |
-10 |
-17 |
| A2
|
5 |
-6 |
-16 |
| A3
|
8 |
14 |
Если имеется несколько клеток с одним и тем же наименьшим значением оценки, то из них выбирается клетка, имеющая наименьший тариф. Наиболее перспективной является клетка (1,5)
. Для нее оценка равна -17
. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Перемещаем по циклу груз величиной в 100 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 8360
Значение целевой функции изменилось на 1700 единиц по сравнению с предыдущим этапом.
Этап 3
Определим значения оценок Si,j
для всех свободных клеток (неоптимальные выделены красным цветом
). Для этого строим цикл для каждой свободной клетки и, перемещаясь по клеткам цикла, складываем тарифы клеток. При этом тарифы в нечетных клетках берутся со знаком "плюс", в четных - со знаком "минус". S1,3
= c1,3
-c1,2
+c2,2
-c2,3
= 12 S1,4
= c1,4
-c1,1
+c3,1
-c3,4
= -10
S2,1
= c2,1
-c2,2
+c1,2
-c1,1
= 5 S2,4
= c2,4
-c2,2
+c1,2
-c1,1
+c3,1
-c3,4
= -6
S2,5
= c2,5
-c2,2
+c1,2
-c1,5
= 1 S3,2
= c3,2
-c3,1
+c1,1
-c1,2
= 8 S3,3
= c3,3
-c3,1
+c1,1
-c1,2
+c2,2
-c2,3
= 14 S3,5
= c3,5
-c3,1
+c1,1
-c1,5
= 17
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
12 |
-10 |
| A2
|
5 |
-6 |
1 |
| A3
|
8 |
14 |
17 |
Если имеется несколько клеток с одним и тем же наименьшим значением оценки, то из них выбирается клетка, имеющая наименьший тариф. Наиболее перспективной является клетка (1,4)
. Для нее оценка равна -10
. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Перемещаем по циклу груз величиной в 110 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 7260
Значение целевой функции изменилось на 1100 единиц по сравнению с предыдущим этапом.
Этап 4
Определим значения оценок Si,j
для всех свободных клеток (неоптимальные выделены красным цветом
). Для этого строим цикл для каждой свободной клетки и, перемещаясь по клеткам цикла, складываем тарифы клеток. При этом тарифы в нечетных клетках берутся со знаком "плюс", в четных - со знаком "минус". S1,1
= c1,1
-c1,4
+c3,4
-c3,1
= 10 S1,3
= c1,3
-c1,2
+c2,2
-c2,3
= 12 S2,1
= c2,1
-c2,2
+c1,2
-c1,4
+c3,4
-c3,1
= 15 S2,4
= c2,4
-c2,2
+c1,2
-c1,4
= 4 S2,5
= c2,5
-c2,2
+c1,2
-c1,5
= 1 S3,2
= c3,2
-c3,4
+c1,4
-c1,2
= -2
S3,3
= c3,3
-c3,4
+c1,4
-c1,2
+c2,2
-c2,3
= 4 S3,5
= c3,5
-c3,4
+c1,4
-c1,5
= 7
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
10 |
12 |
| A2
|
15 |
4 |
1 |
| A3
|
-2 |
4 |
7 |
Если имеется несколько клеток с одним и тем же наименьшим значением оценки, то из них выбирается клетка, имеющая наименьший тариф. Наиболее перспективной является клетка (3,2)
. Для нее оценка равна -2
. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Перемещаем по циклу груз величиной в 160 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 6940
Значение целевой функции изменилось на 320 единиц по сравнению с предыдущим этапом.
Этап 5
Определим значения оценок Si,j
для всех свободных клеток (неоптимальные выделены красным цветом
). Для этого строим цикл для каждой свободной клетки и, перемещаясь по клеткам цикла, складываем тарифы клеток. При этом тарифы в нечетных клетках берутся со знаком "плюс", в четных - со знаком "минус". S1,1
= c1,1
-c1,4
+c3,4
-c3,1
= 10 S1,2
= c1,2
-c1,4
+c3,4
-c3,2
= 2 S1,3
= c1,3
-c1,4
+c3,4
-c3,2
+c2,2
-c2,3
= 14 S2,1
= c2,1
-c2,2
+c3,2
-c3,1
= 13 S2,4
= c2,4
-c2,2
+c3,2
-c3,4
= 2 S2,5
= c2,5
-c2,2
+c3,2
-c3,4
+c1,4
-c1,5
= -1
S3,3
= c3,3
-c3,2
+c2,2
-c2,3
= 6 S3,5
= c3,5
-c3,4
+c1,4
-c1,5
= 7
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
10 |
2 |
14 |
| A2
|
13 |
2 |
-1 |
| A3
|
6 |
7 |
Если имеется несколько клеток с одним и тем же наименьшим значением оценки, то из них выбирается клетка, имеющая наименьший тариф. Наиболее перспективной является клетка (2,5)
. Для нее оценка равна -1
. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Перемещаем по циклу груз величиной в 20 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 6920
Значение целевой функции изменилось на 20 единиц по сравнению с предыдущим этапом.
Этап 6
Определим значения оценок Si,j
для всех свободных клеток (неоптимальные выделены красным цветом
). Для этого строим цикл для каждой свободной клетки и, перемещаясь по клеткам цикла, складываем тарифы клеток. При этом тарифы в нечетных клетках берутся со знаком "плюс", в четных - со знаком "минус". S1,1
= c1,1
-c1,5
+c2,5
-c2,2
+c3,2
-c3,1
= 9 S1,2
= c1,2
-c1,5
+c2,5
-c2,2
= 1 S1,3
= c1,3
-c1,5
+c2,5
-c2,3
= 13 S2,1
= c2,1
-c2,2
+c3,2
-c3,1
= 13 S2,4
= c2,4
-c2,5
+c1,5
-c1,4
= 3 S3,3
= c3,3
-c3,2
+c2,2
-c2,3
= 6 S3,4
= c3,4
-c3,2
+c2,2
-c2,5
+c1,5
-c1,4
= 1 S3,5
= c3,5
-c3,2
+c2,2
-c2,5
= 8
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
9 |
1 |
13 |
| A2
|
13 |
3 |
| A3
|
6 |
1 |
8 |
Так как все оценки Si,j
>=0, то полученный план является оптимальным. Транспортная задача решена.
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 6920
2) Метод потенциалов
Примем некоторые обозначения: i
- индекс строки j
- индекс столбца m
- количество поставщиков n
- количество потребителей Xi,j
- перевозка между поставщиком Ai
и потребителем Bj
.
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Транспортная задача имеет закрытый тип, так как суммарный запас груза равен суммарным потребностям. Находим опорный план по правилу северо-западного угла: Введем некоторые обозначения: Ai
*
- излишек нераспределенного груза от поставщика Ai
Bj
*
- недостача в поставке груза потребителю Bj
Помещаем в клетку (1,1) меньшее из чисел A1
*
=370 и B1
*
=300 Так как спрос потребителя B1
удовлетворен, то столбец 1 в дальнейшем в расчет не принимается Помещаем в клетку (1,2) меньшее из чисел A1
*
=70 и B2
*
=280 Так как запасы поставщика A1
исчерпаны, то строка 1 в дальнейшем в расчет не принимается Помещаем в клетку (2,2) меньшее из чисел A2
*
=450 и B2
*
=210 Так как спрос потребителя B2
удовлетворен, то столбец 2 в дальнейшем в расчет не принимается Помещаем в клетку (2,3) меньшее из чисел A2
*
=240 и B3
*
=330 Так как запасы поставщика A2
исчерпаны, то строка 2 в дальнейшем в расчет не принимается Помещаем в клетку (3,3) меньшее из чисел A3
*
=480 и B3
*
=90 Так как спрос потребителя B3
удовлетворен, то столбец 3 в дальнейшем в расчет не принимается Помещаем в клетку (3,4) меньшее из чисел A3
*
=390 и B4
*
=290 Так как спрос потребителя B4
удовлетворен, то столбец 4 в дальнейшем в расчет не принимается Помещаем в клетку (3,5) меньшее из чисел A3
*
=100 и B5
*
=100
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F=11320
Решаем задачу методом потенциалов:
Этап 1
Полагая потенциал U1
=0, определяем остальные потенциалы из соотношения Ui
+Vj
=Ci,j
(i=1..m, j=1..n)
, просматривая все занятые клетки. Потенциалы Ui
, Vj
: U1
=0 V1
=C1,1
-U1
= 14
V2
=C1,2
-U1
= 8
U2
=C2,2
-V2
= 2
V3
=C2,3
-U2
= 5
U3
=C3,3
-V3
= 3
V4
=C3,4
-U3
= 1
V5
=C3,5
-U3
= 6
Определяем значения оценок Si,j
=Ci,j
-(Ui
+Vj
)
для всех свободных клеток (неоптимальные выделены красным цветом
) S1,3
= c1,3
- (u1
+ v3
) = 12. S1,4
= c1,4
- (u1
+ v4
) = 4. S1,5
= c1,5
- (u1
+ v5
) = -3.
S2,1
= c2,1
- (u2
+ v1
) = 5. S2,4
= c2,4
- (u2
+ v4
) = 8. S2,5
= c2,5
- (u2
+ v5
) = -2.
S3,1
= c3,1
- (u3
+ v1
) = -14.
S3,2
= c3,2
- (u3
+ v2
) = -6.
Если имеется несколько клеток с одним и тем же наименьшим значением оценки, то из них выбирается клетка, имеющая наименьший тариф. Наиболее потенциальной является клетка (3,1)
. Для нее оценка равна -14
. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Перемещаем по циклу груз величиной в 90 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 10060
Значение целевой функции изменилось на 1260 единиц по сравнению с предыдущим этапом.
Этап 2
Полагая потенциал U1
=0, определяем остальные потенциалы из соотношения Ui
+Vj
=Ci,j
(i=1..m, j=1..n)
, просматривая все занятые клетки. Потенциалы Ui
, Vj
: U1
=0 V1
=C1,1
-U1
= 14
V2
=C1,2
-U1
= 8
U3
=C1,3
-V1
= -11
U2
=C2,2
-V2
= 2
V3
=C2,3
-U2
= 5
V4
=C3,4
-U3
= 15
V5
=C3,5
-U3
= 20
Определяем значения оценок Si,j
=Ci,j
-(Ui
+Vj
)
для всех свободных клеток (неоптимальные выделены красным цветом
) S1,3
= c1,3
- (u1
+ v3
) = 12. S1,4
= c1,4
- (u1
+ v4
) = -10.
S1,5
= c1,5
- (u1
+ v5
) = -17.
S2,1
= c2,1
- (u2
+ v1
) = 5. S2,4
= c2,4
- (u2
+ v4
) = -6.
S2,5
= c2,5
- (u2
+ v5
) = -16.
S3,2
= c3,2
- (u3
+ v2
) = 8. S3,3
= c3,3
- (u3
+ v3
) = 14. Если имеется несколько клеток с одним и тем же наименьшим значением оценки, то из них выбирается клетка, имеющая наименьший тариф. Наиболее потенциальной является клетка (1,5)
. Для нее оценка равна -17
. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
| Поставщик |
Потребитель |
Запасы груза |
| B1 |
B2 |
B3 |
B4 |
B5 |
| A1 |
|
|
|
|
|
370 |
| A2 |
|
|
|
|
|
450 |
| A3 |
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Перемещаем по циклу груз величиной в 100 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
| Поставщик |
Потребитель |
Запасы груза |
| B1 |
B2 |
B3 |
B4 |
B5 |
| A1 |
|
|
|
|
|
370 |
| A2 |
|
|
|
|
|
450 |
| A3 |
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 8360
Значение целевой функции изменилось на 1700 единиц по сравнению с предыдущим этапом.
Этап 3
Полагая потенциал U1
=0, определяем остальные потенциалы из соотношения Ui
+Vj
=Ci,j
(i=1..m, j=1..n)
, просматривая все занятые клетки. Потенциалы Ui
, Vj
: U1
=0 V1
=C1,1
-U1
= 14
V2
=C1,2
-U1
= 8
V5
=C1,5
-U1
= 3
U3
=C1,3
-V1
= -11
U2
=C2,2
-V2
= 2
V3
=C2,3
-U2
= 5
V4
=C3,4
-U3
= 15
Определяем значения оценок Si,j
=Ci,j
-(Ui
+Vj
)
для всех свободных клеток (неоптимальные выделены красным цветом
) S1,3
= c1,3
- (u1
+ v3
) = 12. S1,4
= c1,4
- (u1
+ v4
) = -10.
S2,1
= c2,1
- (u2
+ v1
) = 5. S2,4
= c2,4
- (u2
+ v4
) = -6.
S2,5
= c2,5
- (u2
+ v5
) = 1. S3,2
= c3,2
- (u3
+ v2
) = 8. S3,3
= c3,3
- (u3
+ v3
) = 14. S3,5
= c3,5
- (u3
+ v5
) = 17. Если имеется несколько клеток с одним и тем же наименьшим значением оценки, то из них выбирается клетка, имеющая наименьший тариф. Наиболее потенциальной является клетка (1,4)
. Для нее оценка равна -10
. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Перемещаем по циклу груз величиной в 110 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
| Поставщик |
Потребитель |
Запасы груза |
| B1 |
B2 |
B3 |
B4 |
B5 |
| A1 |
|
|
|
|
|
370 |
| A2 |
|
|
|
|
|
450 |
| A3 |
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 7260
Значение целевой функции изменилось на 1100 единиц по сравнению с предыдущим этапом.
Этап 4
Полагая потенциал U1
=0, определяем остальные потенциалы из соотношения Ui
+Vj
=Ci,j
(i=1..m, j=1..n)
, просматривая все занятые клетки. Потенциалы Ui
, Vj
: U1
=0 V2
=C1,2
-U1
= 8
V4
=C1,4
-U1
= 5
V5
=C1,5
-U1
= 3
U2
=C2,2
-V2
= 2
U3
=C4,3
-V4
= -1
V3
=C2,3
-U2
= 5
V1
=C3,1
-U3
= 4
Определяем значения оценок Si,j
=Ci,j
-(Ui
+Vj
)
для всех свободных клеток (неоптимальные выделены красным цветом
) S1,1
= c1,1
- (u1
+ v1
) = 10. S1,3
= c1,3
- (u1
+ v3
) = 12. S2,1
= c2,1
- (u2
+ v1
) = 15. S2,4
= c2,4
- (u2
+ v4
) = 4. S2,5
= c2,5
- (u2
+ v5
) = 1. S3,2
= c3,2
- (u3
+ v2
) = -2.
S3,3
= c3,3
- (u3
+ v3
) = 4. S3,5
= c3,5
- (u3
+ v5
) = 7. Если имеется несколько клеток с одним и тем же наименьшим значением оценки, то из них выбирается клетка, имеющая наименьший тариф. Наиболее потенциальной является клетка (3,2)
. Для нее оценка равна -2
. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Перемещаем по циклу груз величиной в 160 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 6940
Значение целевой функции изменилось на 320 единиц по сравнению с предыдущим этапом.
Этап 5
Полагая потенциал U1
=0, определяем остальные потенциалы из соотношения Ui
+Vj
=Ci,j
(i=1..m, j=1..n)
, просматривая все занятые клетки. Потенциалы Ui
, Vj
: U1
=0 V4
=C1,4
-U1
= 5
V5
=C1,5
-U1
= 3
U3
=C4,3
-V4
= -1
V1
=C3,1
-U3
= 4
V2
=C3,2
-U3
= 6
U2
=C2,2
-V2
= 4
V3
=C2,3
-U2
= 3
Определяем значения оценок Si,j
=Ci,j
-(Ui
+Vj
)
для всех свободных клеток (неоптимальные выделены красным цветом
) S1,1
= c1,1
- (u1
+ v1
) = 10. S1,2
= c1,2
- (u1
+ v2
) = 2. S1,3
= c1,3
- (u1
+ v3
) = 14. S2,1
= c2,1
- (u2
+ v1
) = 13. S2,4
= c2,4
- (u2
+ v4
) = 2. S2,5
= c2,5
- (u2
+ v5
) = -1.
S3,3
= c3,3
- (u3
+ v3
) = 6. S3,5
= c3,5
- (u3
+ v5
) = 7. Если имеется несколько клеток с одним и тем же наименьшим значением оценки, то из них выбирается клетка, имеющая наименьший тариф. Наиболее потенциальной является клетка (2,5)
. Для нее оценка равна -1
. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Перемещаем по циклу груз величиной в 20 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 6920
Значение целевой функции изменилось на 20 единиц по сравнению с предыдущим этапом.
Этап 6
Полагая потенциал U1
=0, определяем остальные потенциалы из соотношения Ui
+Vj
=Ci,j
(i=1..m, j=1..n)
, просматривая все занятые клетки.
Потенциалы Ui
, Vj
: U1
=0 V4
=C1,4
-U1
= 5
V5
=C1,5
-U1
= 3
U2
=C5,2
-V5
= 3
V2
=C2,2
-U2
= 7
V3
=C2,3
-U2
= 4
U3
=C2,3
-V2
= -2
V1
=C3,1
-U3
= 5
Определяем значения оценок Si,j
=Ci,j
-(Ui
+Vj
)
для всех свободных клеток (неоптимальные выделены красным цветом
) S1,1
= c1,1
- (u1
+ v1
) = 9. S1,2
= c1,2
- (u1
+ v2
) = 1. S1,3
= c1,3
- (u1
+ v3
) = 13. S2,1
= c2,1
- (u2
+ v1
) = 13. S2,4
= c2,4
- (u2
+ v4
) = 3. S3,3
= c3,3
- (u3
+ v3
) = 6. S3,4
= c3,4
- (u3
+ v4
) = 1. S3,5
= c3,5
- (u3
+ v5
) = 8. Так как все оценки Si,j
>=0, то полученный план является оптимальным. Транспортная задача решена.
| Поставщик |
Потребитель |
Запасы груза |
| B1
|
B2
|
B3
|
B4
|
B5
|
| A1
|
|
|
|
|
|
370 |
| A2
|
|
|
|
|
|
450 |
| A3
|
|
|
|
|
|
480 |
| Потребность |
300 |
280 |
330 |
290 |
100 |
Целевая функция F= 6920
|