Реферат: Електричні властивості молекул. Поведінка речовини в зовнішньому електричному полі
|
Название: Електричні властивості молекул. Поведінка речовини в зовнішньому електричному полі Раздел: Рефераты по химии Тип: реферат | ||||||||||||
| Електричні властивості молекул. Поведінка речовини в зовнішньому електричному полі Всі молекули, що мають ковалентний зв’язок, можна розділити на два типи: полярні і неполярні. Якщо будь-яку молекулу з ковалентним зв’язком розмістити у зовнішнє електричне поле, то в молекулі спостерігається зміщення електронної густини і виникає індукований дипольний момент. В електричному полі крім зміщення електронної густини спостерігається і деяке зміщення атомів, а також орієнтація індукованого дипольного моменту вздовж силових ліній зовнішнього поля. Зміщення електронів, атомів та орієнтація молекул у зовнішньому полі називається поляризацією (Р). Загальна поляризація: Р = Рел + Рат + Рорієнт . Власний дипольний момент буде виникати в молекулах, атоми яких мають різну електронегативність. На більш електронегативному атомі утворюється надлишок негативного електронного заряду, а на менш електронегативному – надлишок позитивного заряду. Така молекула буде диполем. Дипольний момент μ0 молекули виразиться формулою: μ0 = q · l, де q – заряд, l – віддаль між зарядами, μ0 – вектор, напрямок якого проходить від від’ємного до додатного заряду. В системі СІ μ0 вимірюється в Кул · м. Крім того, μ0 прийнято виражати в дебаях (D): 1D = 3,34 · 10–30 Кул · м. Дипольний момент зв’язаний із симетрією молекул. Полярні молекули належать до точкових груп Сn або Сnv , тобто молекули характеризуються наявністю тільки осей симетрії або осей симетрії і площин симетрії, що перетинаються вздовж цих осей. Молекули, що мають центр симетрії, дипольним моментом не володіють. У молекулах з віссю симетрії – дипольний момент завжди направлений вздовж цієї осі. При наявності площини симетрії вектор дипольного моменту лежить в цій площині. Дипольний момент ізольованої молекули називається власним, або постійним дипольним моментом. При поляризації молекул в електричному полі виникає індукований дипольний момент με , який обумовлений зміщенням електронної густини у молекулі: με = α · Е, де α – коефіцієнт поляризуємості, Е – напруга зовнішнього електричного поля. Причини виникнення дипольних моментів у молекулах. У двохатомній молекулі типу АВ дипольний момент буде виникати тоді, якщо електронна густина в ній зміщена до одного з атомів. Зміщення електронної густини визначається потенціалом іонізації та спорідненістю електронів атомів, що входять до складу молекули. Потенціал іонізації (І) визначається енергією відриву електрона від ізольованого атому. Для більшості хімічних елементів потенціали іонізації визначені і встановлена їх періодична залежність: по періодах (зліва направо) потенціал іонізації зменшується, а в групах (зверху вниз) збільшується. Це пояснюється закономірною періодичною зміною атомних радіусів елементів. У відповідності з прийнятою термінологією енергію відриву першого, другого і т. д. електрона називають першим, другим і т. д. потенціалом іонізації. По мірі послідовного відриву електронів потенціал іонізації зростає. Ця залежність описується рівнянням Глокнера-Янсицина: І = a + bq + cq2 + …, де a, b, c – специфічні коефіцієнти для кожного атома; q – заряд іона. Для нейтрального атома q = 0, тоді І = а. Якщо уявити молекулу як деякий об’єднаний атом, то можна констатувати, що середня статистична віддаль між ядром і зовнішнім електроном буде більша ніж в ізольованого атома. Звідси випливає, що у випадку ковалентних молекул з σ-зв’язком потенціал іонізації молекули буде меншим ніж в ізольованого атома (за винятком молекули Н2 , оскільки у молекулі відсутні внутрішні електрони). При утворенні π-зв’язків центри ваги електронної хмари знаходяться не в міжядерній області, що приводить до зростання взаємодії ядра із зовнішніми електронами, що в свою чергу приведе до зростання потенціалу іонізації молекули порівняно з ізольованим атомом. З ростом кратності зв’язку потенціал іонізації молекули також зростає. Величина спорідненості до електрона рівна енергії, яка виділяється при приєднанні електрона до нейтрального атома: А + Для більшості елементів спорідненість до електрону більше 0 (СЕ > 0). Це означає, що електронейтральний атом притягує додатковий електрон так, ніби в нього є деякий додатній заряд. Цей заряд обумовлений тим, що власні електрони атома не повністю нейтралізують заряд ядра. В результаті на зовнішній електрон кожного атома (крім Н) діє ефективний заряд ядра z* > 1. Згідно інтерпретації Слетера можна вважати, що чим ближче до ядра знаходиться електрон, тим повніше буде нейтралізований заряд. Слетер вивів наступні правила: 1. На електрон, що знаходиться на даній оболонці, діє заряд ядра (рівний його атомному номеру z), зменшений на число останніх електронів, помножений на константу екранування (σ) кожного електрона, причому: 1) електрон на зовнішній оболонці має σ = 0,35; 2) електрон на попередній оболонці має σ = 0,85; 3) електрон більш глибоких оболонок має σ = 1; 4) у випадку d, f-елементів σ = 1. Наприклад: ефективний заряд ядра для Рb визначається так: ZPb = 82; n = 6: n = 6, σ = 0,35 для електронів зовнішньої оболонки (n = 6); n = 5, σ = 0,85 для електронів, що знаходяться на 5-ій оболонці; n = 1–4, σ = 1 для електронів 4, 3,2, 1 оболонці. z = 82; число електронів на 6-ій оболонці – 4, число електронів на 5-ій оболонці – 18, число електронів на 4, 3, 2, 1 – 60. Тоді ZPb * = 82 – 0,35 · 4 – 0,85 · 18 – 1 · 60 = 5,3. Електровід’ємність. Полінг електровід’ємність визначив як здатність атома в молекулі притягувати електрони. Він (1952 р.) відмітив, що для будь-якої пари атомів АВ енергія простого зв’язку А–В, як правило більша, як середня енергія із енергій простих зв’язків А–А і В–В, тобто реакція А2 + В2 ® 2АВ завжди екзотермічна. Це можна пояснити так: зв’язуючу молекулярну орбітель у молекулі АВ можно записати: ψ = ψА + сψВ , де ψA і ψB – атомні орбіталі; ψ – молекулярні орбіталі. а) Якщо коефіцієнт c > 1, то молекулярна орбіталь більше сконцентрована у атома В, який із за цього набуває від’ємний заряд, а атом А, біля якого електронна енергія зменшилась, стає додатньо зарядженим. Таким чином, зв’язок АВ стає полярним: А+ –В– . б) Якщо c < 1, тоді А– –В+ , тобто в молекулі виникає постійний дипольний момент μD = q · d¢ (q – величина заряду; d¢ – віддаль між зарядами. Цей іонний характер зв’язку А–В збільшить його енергію порівняно з тим, що очікувалась у випадку чисто ковалентного зв’язку. Іонна складова ковалентного зв’язку позначається Δ (дельта): Δ = Е(А–В) – де Е(А–В), Е(А–А), Е(В–В) – експериментально визначені енергії вказаних зв’язків. Якщо кожному атому приписати коефіцієнт електровід’ємності х як міру його електровід’ємності, тоді різниця |xA
– xB
| повинна бути зв’язана з с і відповідно з Δ. Полінг запропонував співвідношення: |xA
– xB
| = 0,208 ІА – ЕВ < ІВ – ЕА , ІА + ЕВ < ІВ + ЕА . Маяликен вважав, що сума І + Е є мірою електровід’ємності атома. При відповідному коефіцієнті пропорційності коефіцієнти електровід’ємності в інтерпретації Маяликена добре погоджуються з величинами шкали Полінга. Олрід і Рохав (1958) розглядають електровід’ємність атома як силу притягання між цим атомом і електроном, що знаходиться від ядра на віддалі ковалентного радіуса:
е – заряд електрона (4,80274 · 10–10 ел-ст. д.);
r – ковалентний радіус; F – електростатична сила притягання. F можна зв’язати з шкалою Полінга за допомогою рівняння:
r вимірюється в ангстремах (Å). Приклад. Визначити коефіцієнт електровід’ємності Рb. ZPb = 82: 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 4f14 5s2 5p6 5d10 6s2 6p2 ; rковPb = 1,538Å; Zеф
= 82 – (0,35 ´ число
Мартинов і Богданов запропонували визначати електровід’ємність елементу за формулою: Чим більша електронегативність атомів, що утворили молекулу, тим більший її дипольний момент. Розрахований дипольний момент (q · l) і визначений експериментально для одної молекули не співпадають. Наприклад: μексп (D) μрозр (D) СО 0,11 5,42 HCl 1,04 6,14 HBr 0,79 6,81 KCl 6,8 15,08. Це вказує на те, що навіть у сильно іонних молекулах типу KCl немає повного переносу електрона від одного атома до іншого, а проходить тільки деформація електронної оболонки в напрямку більш електронегативного елементу. Адитивна схема визначення дипольного моменту багатоатомної молекули. В основі схеми визначення дипольного моменту багатоатомної молекули лежить уявлення про те, що основним структурним елементом молекули є валентний зв’язок. Багатоатомну молекулу можна представити як систему хімічних зв’язків, кожен з яких можна розглядати як двохатомну молекулу з своїм дипольним моментом. Тому дипольний момент багатоатомної молекули може бути одержаний як векторна сума дипольних моментів хімічних зв’язків, що входять у молекулу. Ця схема називається адитивною. При векторному сумуванні дипольних моментів хімічних зв’язків обов’язково враховується геометрія молекули і напрямок дипольних моментів кожного зв’язку. Наприклад:
μ1 , μ2 – дипольні моменти хімічних зв’язків; Q – кут між цими хімічними зв’язками.
Якщо μ1
= μ2
= μ, то Якщо молекула має більше, ніж два зв’язки, то проводиться послідовне векторне сумування: до суми двох векторів додають третій, до результату – четвертий і т.д., враховуючи геометричне розташування і напрямок дипольних моментів хімічних зв’язків. Як і для двохатомної молекули, розрахований і експериментально знайдений дипольний момент багатоатомної молекули не співпадають, що може бути пояснено внутрішньомолекулярними взаємодіями атомів. Індукційний і мезомерний ефект. Індукційний ефект – зміщення електронної густини в напрямку більш електровід’ємного атома або групи атомів. Зрозуміло, що зміщення електронної густини проявляється на величині дипольного моменту. Мезомерний ефект – взаємодія π-зв’язків між собою і π-зв’язків з неподіленими р-електронними парами в атомах замісників. π–π-спряження – делокалізація π-зв’язків у бензолі і дієнових вуглеводнях з спряженими зв’язками. Якщо в молекулі є два ефекти, то важливо знати їх напрямки паралельний чи антипаралельний. При переході від нітрометану до нітро-бензолу дипольний момент зростає (індукційний і спряжені ефекти однаково напрямлені). При переході від хлорметана до хлор-бензолу дипольний момент хлорбензола менший, ніж у хлорметана. Неподілені електронні пари Сl вступають у спряження з π-зв’язками, і електронна густина зменшується в напрямку бензольного кільця.
Дипольний момент молекул залежить від геометричної ізомерії: цис- і транс-ізомерія. Молекули в транс-формі завжди мають центр симетрії, тому їх дипольний момент дорівнює 0. Існування поворотних ізомерів молекул також впливає на їх дипольний момент. Наприклад, у молекулі дихлоретану СН2 Сl–CH2 Cl. Якщо вважати, що зв’язок С–Н не вносить значного вкладу в дипольний момент молекули, то її дипольний момент можна визначити як суму дипольних моментів зв’язків С–Сl. Зв’язок дипольного моменту молекули залежить від кута повороту груп СН2 Сl одна відносно іншої
φ – кут повороту.
μцис = 3,4D; μтранс = 0. На величину дипольного моменту дихлоретану впливає температура. Із зростанням температури кількість цис-ізомерів зростає, так як кількість молекул, які можуть перейти через потенціальний бар’єр, зростає. Зрозуміло, що у випадку дихлоретану завжди є суміш цис- і транс-ізомерів. Тоді μ2 = с1 μ1 2 + с2 μ2 2 , c1 – концентрація транс-форми, с2 – концентрація цис-форми. Якщо μ1 = 0, тоді μ2
= с2
μ2
2
;
K – стала Больцмана; ΔЕ – величина потенціального бар’єру і ΔЕ = –KTlnKрів . По температурній залежності дипольного моменту газу можна знайти концентрації ізомерів, через них знайти Kрів , а черех Kрів – величину потенціального бар’єру, що відділяє два ізомери. Вивчаючи дипольні моменти молекул, які здатні до поворотної ізомерії, можна одержати відомості про поворотну ізомерію. З дипольних моментів можна судити про геометрію молекул і їх симетрію. Але вирішити однозначно про геометрію молекули, виходячи з дипольних моментів, неможливо, можна лише припустити ту чи іншу форму молекули. Поляризуємість молекул. Тензор поляризуємості. Якщо речовину помістити в електричне поле (Е), то заряджені частки молекули (електрони і ядра) зміщуються з своїх положень у напрямку силових ліній прикладеного поля. В молекулах виникає індукований дипольний момент, величина якого пропорційна напрузі прикладеного поля: μ2 = α · Е, α – коефіцієнт пропорційності, який характеризує поляризуємість молекули.
тобто поляризуємість молекули вимірюється в одиницях об’єму. α показує – наскільки сильно деформується електронна оболонка молекули під дією зовнішнього електричного поля. Різні молекули при одному і тому ж значенні Е будуть мати різні α. α буде скалярною величиною лише в тому випадку, якщо під дією сил електричного поля зміщення електронної густини молекули у всіх трьох взаємно перпендикулярних напрямках буде однаковим. В загальному випадку зміщення електронної густини у трьох напрямках, як правило, різне: найбільше зміщення електронної густини спостерігається у тому напрямку, який співпадає з напрямком прикладного поля. У загальному випадку:
де x, k, y i z – цілі величини. αik може бути записане у вигляді тензора
αхх – зміщення електронної оболонки вздовж осі х, якщо напруга прикладена по осі х; αху – зміщення по осі х, якщо поле прикладене по осі у; αхz – зміщення по осі х, якщо поле прикладене по осі z. Найбільшу величину мають діагональні складові тензора. Крім того, доведено, що компоненти тензора, які симетрично розташовані відносно діагоналі, рівні між собою: αху = αух ; αхz = αzх ; αуz = αzу – симетричний тензор. Такий тензор можна звести до діагонального вигляду
Якщо всі три діагональні складові тензора не рівні один одному, то геометричне зображення тензора поляризуємості являє собою 3х-осьовий еліпсоїд. Це випадок анізотропної молекули, яка відноситься до груп низкьої симетрії. Якщо два з трьох діагональних складових рівні, то геометричним образом такого тензора буде двохосьовий еліпсоїд обертання. Такі молекули відносяться до груп середньої симетрії. Якщо всі три складові діагонального тензора рівні між собою, тоді еліпсоїд обертання переходить у кулю, і поляризуємість стає скалярною величиною. Такі молекули відносяться до груп вищої симетрії. Поведінка речовин в електричному полі. Розглянемо явища, які виникають у речовині при розміщенні його в зовнішньому електричному полі. Поля можна розділити на електростатичне, для якого напруга стала, і змінне, для якого напруга з часом змінюється за певним законом. Поведінка речовин у постійному і змінному полях відрізняється. Розглянемо поведінку речовин у постійному полі. Якщо речовину помістити в зовнішньому полі, то в речовині виникає явище поляризації – заряджені частинки – ядра і електрони кожної молекули зміщуються з своїх рівноважних положень в напрямку силових ліній поля. В молекулі виникає індукований полем дипольний момент, який буде пропорційний напрузі прикладеного поля: μінд = α · Е, α – називається поляризуємістю, вимірюваною в одиницях об’єму (см3 ):
Якщо одиниця об’єму містить N атомів (число Лошмідта), то можна ввести поняття поляризації речовини:
(добуток дипольного моменту окремої молекули на число молекул). Підставимо у (2) замість με його значення, тоді Р = NαE. (3) Полярні молекули речовини мають нескомпенсовані електричні заряди, тому напруга поля в речовині не буде рівна напрузі зовнішнього поля. Величина, на яку зміниться напруга поля під дією дипольних моментів молекул, може бути визначена діелектричною проникністю ε. Відомо, що якщо речовина знаходиться в зовнішньому електричному полі, то вона характеризується вектором електричної індукції
Існує цілий розділ фізики, головним завданням якої є знаходження аналітичного зв’язку між макроскопічною характеристикою речовини ( Вся трудність теорії полягає в тому, щоб визначити величину внутрішнього поля, для цього необхідно знати як розміщені молекули одна відносно другої і як вони взаємодіють між собою. Для визначення внутрішнього поля використовують різні моделі, тобто наперед задають розміщення молекул і їх взаємодію. Найпростіша модель – це модель Дебая і Лоренца, згідно якої молекули речовини знаходяться в стані хаосу і не взаємодіють між собою. В цьому випадку Е¢ = Е + Тоді в (3) підставимо Е¢ із (5) замість Е: Р = Nα Е¢ = Nα(Е + З рівняння (4) маємо:
Е(ε – 1) = 4πР, (7)
Прирівнюємо Р із (6) і (8): Nα(Е + У рівняння (9) підставляємо замість Р його значення із (8): Nα Відкриваємо в (10) дужки: NαЕ +
Формула (11) – це формула Клаузиуса-Масотті. Електричні властивості молекул визначаються дипольним моментом та поляризуємістю. Безпосередньо ці величини визначити експериментально неможливо, тому рівняння Клаузиуса-Масотті дає зв’язок між мікрохарактеристиками (μ, α) молекул та макрохарактеристиками ( Використавши зв’язок між N (число молекул в одиниці об’єму) і NA (число Авогадро), рівняння Клаузиуса-Масотті можна записати так: N = де r – питома вага речовини; М – молярна маса речовини
Якщо врахувати орієнтаційний дипольний момент молекул у зовнішньому електричному полі, то рівняння Клаузиуса-Масотті набуває вигляду
Це рівняння називають рівнянням Дебая. Поведінка речовин у змінному електричному полі. Рефракція. При дії на молекули діелектрика змінного поля поляризація залежить від зміни поля. Із збільшенням частоти полярні молекули не встигають орієнтуватися вздовж поля. Тому при досягненні деякої критичної частоти спочатку зникає орієнтаційна поляризація. При дальшому збільшенні частоти зникає і атомна поляризація через інерцію зміщення атомів і атомних груп в молекулі. Таким чином, для частот змінного поля вище 1015 гц спостерігається тільки електронна поляризація. Тому для неполярних діелектриків в полях змінної частоти рівняння Клаузиуса-Масотті заміняється рівнянням молярної рефрекції Лоренц-Лорентца, так як ε(n) = n2 (n) R = n – показник заломлення; α – поляризуємість молекул у змінному електричному полі високої частоти. Як правило, експерименти проводять в полі світової хвилі жовтої лінії спектра. Випромінювання цієї довжини хвилі речовиною, як правило, не поглинається. Цю спектральну характеристику позначають індексом в справа знизу: nD , RD . Оскільки густина речовини залежить від температури (Т), то молярна рефракція теж залежить від температури, на що показує верхній правий індекс: R¥
= Pe
= n = Оскільки n речовин можна визначити досить просто, то уже в кінці ХІХ ст. накопичилося багато рефрактометричних даних, особливо для газів і рідин. При звичайних умовах рідкими є більшість органічних сполук, отже вчення про рефракцію з самого початку розвивалося головним чином на органічних об’єктах. Було встановлено, що в гомологічних рядах молярна рефракція зростає при збільшенні молекулярної маси речовини. Тобто вона виявилась безпосередньо зв’язаною з складом хімічної сполуки. Так, при збільшенні ланцюга у насичених вуглеводнях на одну групу СН2
R зростає на одну і ту є величину: 4,618 см3
. Таке постійне зростання R при появі одної і тої ж групи атомів привело до думки приписати певні величини рефракцій окремим атомам. Великою кількістю дослідників були проведені відповідні розрахунки Використання рефрактометрії для розв’язання структурних задач засновано на порівнянні експериментально виміряних величин з теоретично розрахованими рефракціями для різних варіантів розташування атомів у просторі. При розрахунку молярних рефракцій хімічних сполук необхідно враховувати реальний характер хімічного зв’язку між атомами. Приклад.
Якщо візьмемо два вуглеводні з різним n, то одержимо дві рівняння з невідомими RC і RH . З них можна визначити ці величини. Існують таблиці атомних рефракцій для всіх елементів. Величина атомної рефракції елементу залежить від типу хімічного зв’язку, в якому даний атом бере участь. Наприклад, атом С, що приймає участь у подвійному зв’язку, має значення R = = 4,161 см3 , тоді RC= = RC + I=, I= – поправка на подвійний зв’язок, називається інкриментом подвійного зв’язку (І=) = 1,713; RC º = RC + Iº, Iº – інкримент потрійного зв’язку. Тоді загальне рівняння для визначення рефракції молекули, що містить будь-які типи зв’язків, можна записати:
перша сума – сума рефракцій атомів, що входять в молекулу; друга сума – поправка (інкримент) до типу хімічного зв’язку. Рефракція – це величина, яка безпосередньо зв’язана з поляризуємістю. Поляризуємість визначається через об’єм електронної оболонки молекули. Виходячи з цього, більш обгрунтованим є визначення рефракції молекули через суму рефракцій хімічних зв’язків, що містяться у молекулі. Система рефракцій хімічних зв’язків має менше число параметрів порівняно з атомною. Між рефракціями атомів і рефракціями хімічних зв’язків існує взаємно однозначна відповідність: їх можна виразити одну через іншу. Наприклад, RC–H . Так як атом Н одновалентний, то його електронна оболонка задіяна тільки в одному хімічному зв’язку. Атом С – чотиривалентний, і якщо вважати, що на кожен зв’язок він витрачає одну електронну оболонку, то на зв’язок С–Н припаде 1/4RC , тоді RCH
= RH
+ Рефракція хімічного зв’язку С–С запишеться: RC–С
= RC=С
= Якщо визначати рефракцію через суму рефракцій хімічних зв’язків, то необхідність в інкриментах відпадає, тому R = Rj – сума рефракцій хімічних зв’язків. Рефракція зв’язку атомів А–В в молекулі АВn рівна: RA–B
= Користуючись адитивністю рефракції, можна розробити експериментальні методи визначення складу сумішей, так як рефракція суміші буде визначатися як сума рефракцій компонентів суміші з урахуванням кількості кожного компоненту. Якщо, наприклад, маємо суміш речовин А і В, і концентрація речовини А – n моль, а речовини В – (1–n) моль, то рефракція суміші запишеться: Rсуміші = RA n + RB (1–n). Знаючи рефракцію речовин А і В, експериментально визначивши рефракцію суміші, можна підрахувати кількості одного і другого компоненту. Адитивність рефракції можна використати для перевірки правильності вибору хімічної формули для нової речовини. Підрахувавши рефракцію як суму рефракцій зв’язків або атомів і визначивши її експериментально, виникає можливість перевірки правильності вибраної графічної формули сполуки. Якщо розрахована і експериментально знайдена R співпадань, то формула вибрана правильно, якщо – ні, то причин неспівпадання може бути дві: формула вибрана неправильно, для певних класів сполук спостерігається розбіжність між розрахованою і експериментально визначеною рефракцією. Ця розбіжність називається екзальтацією рефракції: ΔR = Rексп. – Rрозрах. . Від чого залежить екзальтація рефракції? Наприклад, візьмемо 2 ізомери гексадієна: СН3 – СН = СН – СН = СН – СН3 – гексадієн – 2,4 (Rексп. = 30,64 см3 ); СН2 = СН – СН2 – СН2 – СН = СН2 – гексадієн – 1,5 ( Rексп. = 28,99 см3 ). Число одинарних і подвійних зв’язків у молекулах однакове, тому розраховані рефракції повинні бути також однакові: Rрозрах. = = 28,74 см3 . Експериментальні рефракції цих сполук різні: R1 = = 30,64 см3 , а R2 = 28,99 см3 , тобто розрахунок і експеримент співпадає тільки для другої молекули. Тоді для першої сполуки маємо екзальтацію рефракції 30,64 – 28,74 = 1,9 см3 . Вказані два ізомери відрізняються тим, що в першій молекулі є мезомерний ефект, а в другій немає. Тому причиною екзальтації є мезомерний ефект. При визначенні рефракції молекул як суми рефракцій її зв’язків, вважаємо, що електронна оболонка кожного зв’язку локалізована саме на ній. При мезомерному ефекті процес локалізації електронної густини на хімічних зв’язках порушується, тому що проходить усуспільнення електронної густини по всіх зв’язках, що приймають участь у спряженій системі. В такому випадку виділити електронну густину кожного зв’язку неможливо, а реальне значення рефракції вище, ніж розраховане. Так як рефракція безпосередньо зв’язана з показником заломлення: R = Таблиця Залежність R від l для нітроаніліна
Експериментальні методи визначення дипольних моментів і поляризуємості молекул. Визначення дипольних моментів і поляризуємості молекул є важливим експериментальним завданням фізики і хімії. Одним з важливих є метод з використанням формули Дебая: Р = Використавши формулу, можна одночасно визначити і дипольний момент (μ0
) і поляризуємість (α) молекул. Для цього вимірюється молярна поляризація при різних температурах Р = f(T). Експериментально вимірюємо густину речовини (r), визначаємо її молярну масу (М) і вимірюємо її діелектричну проникність (ε) при різних температурах: ε = На основі одержаних вимірювань будують графік залежності Р від 1/Т Залежність Р від 1/Т виражається прямою лінією, нахиленої до осі абсцис під кутом φ. Для визначення α і μ0 рівняння Дебая піддаємо перетворенню і вводимо деякі позначення. Відкриваємо дужки у правій частині рівняння. Р = А = tg φ = A = ΔP; ΔP = ΔP не залежить від температури. Другий метод полягає у визначенні різниці між молекулярною поляризацією і молекулярною поляризацією і молекулярною рефракцією: Р = P – R = Теорема буде справедлива, якщо поляризуємість (α), що входить в формулу молекулярної рефракції і поляризуємість (α), що входить у формулу молекулярної поляризації, рівні між собою. Це співпадання спостерігається тільки в граничному випадку:
Тому формулу для визначення μ0 прийнято записувати Р – Щоб скористатися цією формулою, потрібно при фіксованій температурі виміряти молекулярну поляризацію і молекулярну рефракцію, виміряти показник заломлення, діелектричну проникність і густину речовин. Показник заломлення вимірюється при різних довжинах хвиль і будується графік залежності n = f При
Мал. Залежність показника заломлення від довжини хвилі. |
 ,
, ,
,


 ,
,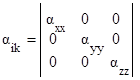 .
. .
. =
= 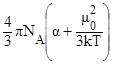 .
. ;
;  ; R =
; R = 