Определение координат оптимального расположения двух складов в регионе
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ »
Кафедра прикладной математики
КУРСОВАЯ РАБОТА
по курсу «Экономико-математические методы и модели»
на тему «Определение координат расположения двух складов в регионе»
Выполнил ст. гр.
УК-06 Ушков О. А.
Проверил доцент
Лубенец Ю. В.
Липецк – 2010
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
РАСПОЛОЖЕНИЕ ПОСТАВЩИКОВ И КЛИЕНТОВ
ОПРЕДЕЛЕНИЕ КООРДИНАТ ПЕРВОГО СКЛАДА
ОПРЕДЕЛЕНИЕ КООРДИНАТ ВТОРОГО СКЛАДА
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
Перемещение материальных потоков в логистической цепи практически невозможно без их концентрации на складах. Цена товара в значительной степени зависит от затрат, связных со складированием распределяемой продукции и с расстоянием, методами и средствами доставки товара от склада до потребителя. В следствие с этим большое значение имеет задача оптимизации размещения распределительного склада. В идеале он должен быть расположен таким образом, чтобы суммарные затраты, связанные с доставкой товаров потребителям, были минимальны.
В данной работе рассмотрено определение координат оптимального расположения двух складов минеральной воды в городе Липецке.
РАСПОЛОЖЕНИЕ ПОСТАВЩИКОВ И КЛИЕНТОВ
Расположение поставщиков (производителей) и клиентов (потребителей) минеральной воды определим с помощью «Липецкой информационной системы» (ЛИС). Масштаб выберем как показано на рисунке 1. Осями координат будут края видимой части карты города. Левый край – ось Y, нижний – ось X. Все точки поставщиков и клиентов прономеруем.

Рисунок 1 – Расположение поставщиков и клиентов
В итоге получаем координаты производителей и потребителей, представленные в таблице 1.
Таблица 1 – Координаты поставщиков и клиентов
| №
|
Х
|
У
|
Показатель
|
Название
|
| 1
|
2309
|
890
|
Клиент
|
«Живая вода»
|
| 2
|
2778
|
4150
|
Поставщик
|
«Эдельвейс Л», ООО
|
| 3
|
3090
|
3975
|
Поставщик
|
«Бриз», ООО
|
| 4
|
3256
|
5890
|
Поставщик
|
«Живая вода», ЗМВ
|
| 5
|
4540
|
4760
|
Поставщик
|
«Делан-Воронеж», ООО
|
| 6
|
5160
|
3200
|
Поставщик
|
«Аква Экспресс»
|
| 7
|
5685
|
2300
|
Поставщик
|
«Императоръ», ООО
|
| 8
|
7340
|
1730
|
Клиент
|
«METRO»
|
| 9
|
7405
|
2980
|
Клиент
|
«Хорошие воды»
|
| 10
|
7480
|
2730
|
Поставщик
|
«Чистый Родник»
|
| 11
|
7480
|
2480
|
Клиент
|
«Живая вода»
|
| 12
|
7610
|
3310
|
Поставщик
|
«Пилар», ТПО, ООО
|
| 13
|
7680
|
3130
|
Клиент
|
«Леда», торговый дом
|
| 14
|
7800
|
4680
|
Клиент
|
«Росинка», фирм. маг. №5
|
| 15
|
7800
|
3170
|
Поставщик
|
Маркитан Ю.А., офиц. дилер завода «Эдельвейс»
|
Средний спрос на минеральную воду в регионе составляет 55000 рублей. А среднее производство минеральной воды – 50000 рублей.
Поставщикам и клиентам расставим коэффициенты от 0,1 до 1, в зависимости от площади здания, где они находятся. Площадь определяем с помощью ЛИС.
Количество товара, перевозимого от производителей и потребителей определим перемножив соответствующий коэффициент на средний спрос и среднее производство минеральной воды, как показано в таблицах 2 и 3.
Таблица 2 – Поставщики
| Поставщики
|
| №
|
Х
|
У
|
Коэффициент производства
|
Количество товара
|
| 1
|
2778
|
4150
|
0,8
|
40000
|
| 2
|
3090
|
3975
|
0,2
|
10000
|
| 3
|
3256
|
5890
|
1
|
50000
|
| 4
|
4540
|
4760
|
0,4
|
20000
|
| 5
|
5160
|
3200
|
0,2
|
10000
|
| 6
|
5685
|
2300
|
0,6
|
30000
|
| 7
|
7480
|
2730
|
0,3
|
15000
|
| 8
|
7610
|
3310
|
0,1
|
5000
|
| 9
|
7800
|
3170
|
0,1
|
5000
|
Таблица 3 – Клиенты
| Клиенты
|
| №
|
Х
|
У
|
Коэффициент спроса
|
Количество товара
|
| 1
|
2309
|
890
|
0,7
|
38500
|
| 2
|
7340
|
1730
|
0,9
|
49500
|
| 3
|
7405
|
2980
|
0,1
|
5500
|
| 4
|
7480
|
2480
|
0,8
|
44000
|
| 5
|
7680
|
3130
|
0,5
|
27500
|
| 6
|
7800
|
4680
|
0,4
|
22000
|
Расстояние между объектами определим как корень квадратный из суммы квадратов разностей их координат. Введем условие примерного равенства складов, чтобы задача не стала многокритериальной.
В работе рассмотрим итерационный алгоритм поиска складов. Выберем эврестически координаты первого и второго складов, затем решим транспортную задачу с помощью Excel модулем «Поиск решения». Затем будем менять координаты только одного склада и выберем вариант где общее расстояние от поставщиков и потребителей будет минимальным (Расчеты осуществляем в Excel). Когда найдем эти оптимальные координаты первого склада, зафиксируем их и приступим к поиску координат второго склада, таким же образом.
ОПРЕДЕЛЕНИЕ КООРДИНАТ ПЕРВОГО СКЛАДА
Итерация 1.
Выбираем координаты складов эврестическим методом, то есть интуитивно. Первый возьмем так: (3750; 3200), а второй – (7550; 3115).
С использованием Excel, находим расстояния от поставщиков до первого и второго складов (таблица 4).
Таблица 4 – Расстояния от поставщиков до первого и второго складов
| Склад Поставщик
|
1
|
2
|
Количество товара
|
| 1
|
1359,148263
|
4882,95085
|
40000
|
| 2
|
1017,951374
|
4542,158077
|
10000
|
| 3
|
2734,983729
|
5112,637382
|
50000
|
| 4
|
1748,628034
|
3430,178567
|
20000
|
| 5
|
1410
|
2391,511029
|
10000
|
| 6
|
2134,063026
|
2035,300961
|
30000
|
| 7
|
3759,494647
|
391,3118961
|
15000
|
| 8
|
3861,567039
|
204,0220576
|
5000
|
| 9
|
4050,11111
|
255,9785147
|
5000
|
| Количество товара
|
92500
|
92500
|
185000
|
В модуле «Поиск решения» устанавливаем целевую ячейку равную минимальному значению и соответствующие ограничения (рисунок 2). В качестве формулы целевой функции будем использовать функцию «СУММПРОИЗВ», которая перемножает соответствующие элементы заданных массивов и возвращает сумму произведений.

Рисунок 2 – Поиск значения целевой функции
На данном этапе получаем значение целевой функции, которое соответствует общему расстоянию поставок минеральной воды на склады.
Чтобы определить минимальное расстояние от складов до поставщиков введем дополнительную таблицу, заполненную нулями и единицами. Единица соответствует ненулевому значению таблицы, изображенной слева на рисунке 3, а ноль ставится, если в левой таблице в соответствующей ячейке стоит ноль.
С помощью функции «СУММПРОИЗВ» найдем минимальное расстояние от поставщиков до складов, перемножив значения из таблицы 4 и дополнительной таблицы, изображенной слева на рисунке 3.

Рисунок 3 – Определение минимального расстояния от поставщиков до складов
Получаем, что минимальное расстояние от поставщиков до складов, с выбранными координатами, составляет 22794,591 метров.
Далее также при помощи Excel, находим расстояния от клиентов до первого и второго складов (таблица 5).
Таблица 5 – Расстояния от клиентов до первого и второго складов
| Склад Клиент
|
1
|
2
|
Количество товара
|
| 1
|
2722,605554
|
5693,742706
|
38500
|
| 2
|
3879,304061
|
1400,830111
|
49500
|
| 3
|
3661,615081
|
198,1161276
|
5500
|
| 4
|
3798,855091
|
638,846617
|
44000
|
| 5
|
3930,62336
|
130,8625233
|
27500
|
| 6
|
4311,948515
|
1584,842263
|
22000
|
| Количество товара
|
93500
|
93500
|
187000
|
С помощью модуля «Поиск решения» проделываем те же действия, что описаны выше для поставщиков и получаем минимальное расстояние от клиентов до складов, равное 12618,08 метров (рисунок 4).

Рисунок 4 – Определение минимального расстояния от клиентов до складов
И последним шагом на данной итерации будет определение общего минимального расстояния, путем сложения минимального расстояния от клиентов до складов и минимального расстояния от поставщиков до складов:
  . .
Таким образом получили, что от складов с координатами (3750; 3200) и (7550; 3115) минимальное расстояние до поставщиков и клиентов будет равно  . .
Итерация 2.
С помощью ЛИС смотрим, как можно поменять координаты первого склада, где его расположить, и меняем предыдущие координаты первого склада на (3333; 3355). Второй склад оставляем на том же месте.
В табличном процессоре MS Excel повторяем действия первой итерации и находим минимальное расстояние от поставщиков и клиентов до складов равное 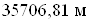 . .
Как видно, при таких координатах первого склада, общее расстояние увеличилось, значит необходимо на следующей итерации искать расположение склада в другом направлении.
Таким образом будем менять координаты первого склада и сравнивать общее расстояние. В итоге выберем минимальное.
Дальнейшие итерации приведены в таблице 6.
Таблица 6 – Расчеты минимального расстояния
| № итерации
|
Координаты первого склада, м
|
Общее минимальное расстояние, м
|
| 1
|
(3750; 3200)
|
35412,67
|
| 2
|
(3333; 3355)
|
35706,81
|
| 3
|
(3090; 3745)
|
35654,7
|
| 4
|
(4454; 3115)
|
35188,16
|
| 5
|
(4810; 3470)
|
35096,1
|
| 6
|
(5860; 3920)
|
36274,82
|
| 7
|
(5860; 3147)
|
35657,99
|
| 8
|
(5086; 3354)
|
35198,61
|
| 9
|
(4800; 4095)
|
35561,08
|
| 10
|
(5120; 2670)
|
35694,68
|
| 11
|
(4530; 3125)
|
35174,15
|
| 12
|
(4585; 3500)
|
35035,22
|
| 13
|
(4356; 3430)
|
35017,75
|
| 14
|
(4335; 3888)
|
35121,73
|
| 15
|
(4245; 3050)
|
35297,29
|
| 16
|
(3845; 3520)
|
35082,18
|
| 17
|
(4160; 3460)
|
35021,24
|
| 18
|
(4585; 3500)
|
35035,22
|
Как видно, общее минимальное расстояние получилось на 13 итерации с координатами первого склада (4356; 3430) и второго (7550; 3115). Первый склад на данном месте и оставляем, его координаты оптимальны.
ОПРЕДЕЛЕНИЕ КООРДИНАТ ВТОРОГО СКЛАДА
Определим оптимальное расположение второго склада. Так как необходимое расположение первого склада найдено, то его расстояние от поставщиков и клиентов на каждой итерации будем оставлять неизменным. Расчеты производятся аналогично определению кординат первого склада.
В таблицах 7 и 8 представлены расстояния от поставщиков и клиентов соответственно до первого и второго складов для первой итерации.
Таблица 7 – Расстояния от поставщиков до первого и второго складов
| Склад Поставщик
|
1
|
2
|
Количество товара
|
| 1
|
1734,498198
|
4518,737
|
40000
|
| 2
|
1378,325433
|
4178,7708
|
10000
|
| 3
|
2694,735609
|
4762,7761
|
50000
|
| 4
|
1342,667494
|
3073,6298
|
20000
|
| 5
|
836,2511584
|
2040,098
|
10000
|
| 6
|
1744,460088
|
1772,463
|
30000
|
| 7
|
3201,464665
|
564,35804
|
15000
|
| 8
|
3256,21191
|
419,76184
|
5000
|
| 9
|
3453,800226
|
602,07973
|
5000
|
| Количество товара
|
92500
|
92500
|
185000
|
Таблица 8 – Расстояния от клиентов до первого и второго складов
| Склад Клиент
|
1
|
2
|
Количество товара
|
| 1
|
3262,178567
|
5417,6361
|
38500
|
| 2
|
3434,276634
|
1496,5627
|
49500
|
| 3
|
3082,028715
|
315,63428
|
5500
|
| 4
|
3265,252823
|
791,20162
|
44000
|
| 5
|
3337,510449
|
488,36462
|
27500
|
| 6
|
3663,828053
|
1578,4803
|
22000
|
| Количество товара
|
93500
|
93500
|
187000
|
Меняем координаты второго склада и выбираем те, в которых расстояния до поставщиков и клиентов будут минимальными. Итоги расчетов представлены в таблице 9.
Таблица 9 – Расчеты минимального расстояния для второго склада
| № итерации
|
Координаты первого склада, м
|
Общее минимальное расстояние, м
|
| 1
|
(7200; 3220)
|
34935,47
|
| 2
|
(7200; 3720)
|
35968,06
|
| 3
|
(7110; 2630)
|
36146,34
|
| 4
|
(6640; 3200)
|
35701,73
|
| 5
|
(6800; 3145)
|
35429,5
|
| 6
|
(7025; 3215)
|
35094,12
|
| 7
|
(7670; 2850)
|
36027,38
|
| 8
|
(7550; 3800)
|
36797,7
|
| 9
|
(7830; 3320)
|
36299,62
|
| 10
|
(7690; 2930)
|
35855,12
|
| 11
|
(7220; 2755)
|
35586,77
|
| 12
|
(7190; 3000)
|
35045,72
|
| 13
|
(7370; 3500)
|
35387,3
|
| 14
|
(7490; 3150)
|
34924,89
|
| 15
|
(7530; 3000)
|
35159,18
|
| 16
|
(7530; 3000)
|
35159,18
|
| 17
|
(7360; 3171)
|
34869,1
|
После проведения 17 итераций по карте ЛИС стало видно, что нет необходимости в дальнейших поисках, найдены оптимальные координаты первого склада (4356; 3430) и второго (7360; 3171).
Оптимальное расположение двух складов минеральной воды в Липецке найдено. Первый склад имеет координаты (4356; 3430), второй – (7360; 3171). они представлены на рисунке 5 красными кружками. Расположив склады в данных точках, затраты на первозки продукции будут минимальными.

Рисунок 5 – Оптимальное расположение двух складов в регионе
ЗАКЛЮЧЕНИЕ
В данной работе с помощью табличного процессора Excel было найдено оптимальное расположение двух складов минеральной воды в городе Липецке. Перебор координат складов производился эврестическим методом, из полученных результатов выбирался тот, где общее расстояние от поставщиков и клиентов было минимальным. Разместив склады в найденных точках, затраты на первозки минеральной воды будут минимальными.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Лукинский, В.С. Логистика автомобильного транспорта: Учеб. пособие / В. С. Лукинский, В. И. Бережной, Е. В. Бережная и др. – М.: Финансы и статистика, 2004. – 368 с.
2. Таха, Хемди А. Введение в исследование операций, 7-е издание.: Пер. с англ. – Издательский дом «Вильямс», 2005. – 912 с.
3. Миротин, Л.Б. Транспортная логистика: Учебник для транспортных вузов. / Под общей редакцией Л.Б. Миротина. – М.: Издательство «Экзамен», 2003. – 512 с.
|