| Контрольная работа 3.
1. Прибор может работать в двух режимах ¾ нормальном и ненормальном. Нормальный режим встречается в 80% всех случаев работы прибора, ненормальный ¾ в 20%. Вероятность выхода прибора за время t
в нормальном режиме равна 0,1, в ненормальном ¾ 0,7. Найти вероятность выхода прибора из строя за время t
.
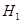 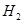 Решение Решение
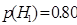 Пусть гипотезы и состоят в том что прибор работает: Пусть гипотезы и состоят в том что прибор работает:
- в нормальном режиме, вероятность
- в ненормальном режиме, вероятность
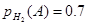 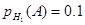 Гипотезы несовместны и сумма их вероятностей равна 1. Значит, гипотезы образуют полную группу. Гипотезы несовместны и сумма их вероятностей равна 1. Значит, гипотезы образуют полную группу.
Пусть событие А состоит в том, что прибор выходит из строя. При условии, что режим работы нормальный, вероятность наступления А равна
При условии что режим работы ненормальный вероятность наступления А
По формуле полной вероятности вычислим вероятность того что прибор выйдет из строя за время t Ответ: 0,22
2. В лотерее каждый десятый билет выигрывает 10 рублей, сам же лотерейный билет стоит 1 рубль. Некто приобрел 10 билетов. Найти вероятность того, что он:
а) не будет в проигрыше;
б) будет в выигрыше.
Решение
Вероятность выиграть по произвольному билету, по формуле классической вероятности равна p=0.1
Проводится n=10 испытаний c одинаковой вероятностью наступления события в каждом.
Для того чтобы игрок не был в проигрыше, должен выиграть хотя бы один билет то есть k>=1
Для того чтобы игрок был в выигрыше, должно выиграть как минимум два билета или k>1
По формуле Бернулли,
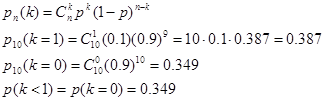
Теперь найдем вероятность противоположного события p(k>=1)=1-p(k<1)=1-0.349=0.651 – вероятность не оказаться в проигрыше
P(k>=1)=p(k>1)+p(k=1) – вероятность суммы несовместных событий
P(k>1)=p(k>=1)-p(k=1)=0.651-0.387=0.264 – вероятность выигрыша
Ответ: а)0,651 б)0,264
3. Семена некоторых растений прорастают с вероятностью 0,8. Найти вероятность того, что из 2000 посаженных семян прорастает:
а) 1600 семян;
б) не менее 1600 семян.
Решение
Мы имеем дело с серией последовательных независимых испытаний, в каждом из которых с одинаковой вероятностью может произойти событие А (семя прорастает)
Количество испытаний n=2000
Вероятность наступления события А равна p(A)=0.8=p
q=1-p=1-0.8=0.2
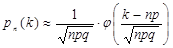 Условия задачи соответствуют схеме Бернулли. В силу того, что n достаточно велико, удобно применить для вычислений локальную теорему Муавра-Лапласа. Вероятность того, что событие А наступит ровно k=1600раз, приблизительно равна Условия задачи соответствуют схеме Бернулли. В силу того, что n достаточно велико, удобно применить для вычислений локальную теорему Муавра-Лапласа. Вероятность того, что событие А наступит ровно k=1600раз, приблизительно равна
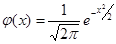
Здесь - локальная функция Лапласа, значения которой можно взять из таблиц.
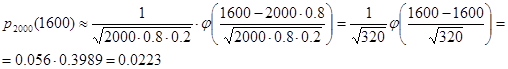 Получим Получим

Ответ :0,0223
4. В коробке лежат 10 исправных и 3 неисправных батарейки. На удачу извлекаются 3 батарейки. Составить закон распределения случайной величины --- числа исправных батареек среди извлеченных.
Решение
Пусть Х- дискретная случайная величина- число неисправных батареек. Х может принимать значения 0,1,2 или 3. Найдем вероятности каждого из значений Х.
Вероятность для каждой батарейки быть неисправной определяем по формуле классической вероятности. Проводится n=3 испытания Бернулли в каждом из которых p=0.231, q=1-p=0.769
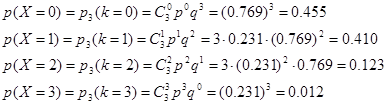 По формуле Бернулли По формуле Бернулли
Проверка: p(X=0)+p(X=1)+p(X=2)+p(X=3)=0.455+0.410+0.123+0.012=1.00
Получаем закон распределения случайной величины Х:
| Х
|
0
|
1
|
2
|
3
|
| Р
|
0,455
|
0,410
|
0,123
|
0,012
|
5. Случайная величина Х распределена по нормальному закону, причем P(X>2) = 0,5, а P(1<X<3) = 0,8. Найти математическое ожидание и дисперсию случайной величины Х.
 Решение Решение
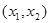 Для случайной величины X с нормальным распределeнием вероятность попадания в интервал равна Для случайной величины X с нормальным распределeнием вероятность попадания в интервал равна
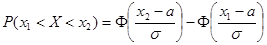
,где Ф(х) – интегральная функция Лапласа,
значения которой табулированы.
По этой формуле
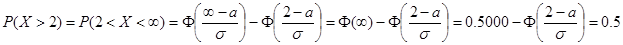
Отсюда следует что Из таблиц определяем a=2 – математическое ожидание Х
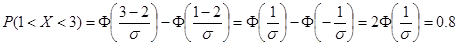 Кроме того Кроме того

Значит
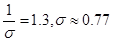
из таблицы определяем что -среднеквадратическое
отклонение
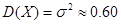 Дисперсия Дисперсия
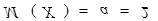 Ответ : Математическое ожидание Ответ : Математическое ожидание
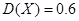 Дисперсия Дисперсия
|