| Контрольная работа № 3
1. Вероятность попадания в цель при залпе из двух орудий равна 0,35. Найти вероятность попадания при одном выстреле первым орудием, если для второго орудия эта вероятность 0,75.
Решение:
Вероятность попадания в цель при залпе из двух орудий равна
 . .
Вероятность попадания при одном выстреле вторым орудием
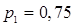 . .
Вероятность попадания при одном выстреле первым орудием
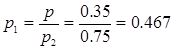
Ответ: 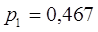
2. Что вероятнее: выиграть у равносильного противника (ничейный результат исключается)
а) 3 партии из 4 или 5 из 8
б) не менее 3 партии из 4 или не менее 5 из 8
Решение:
Вероятность выиграть
 . .
Вероятность проиграть
 . .
а) Что вероятнее: выиграть у равносильного противника (ничейный результат исключается) 3 партии из 4 или 5 из 8:
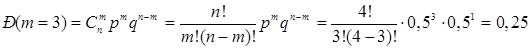

Вероятнее выиграть 3 партии из 4, чем 5 из 8
б) Что вероятнее: выиграть у равносильного противника (ничейный результат исключается) не менее 3 партии из 4 или не менее 5 из 8:



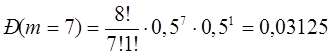

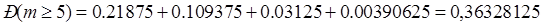
0,3125 < 0,36328125
Вероятнее выиграть не менее 5 партии из 8, чем не менее 3 из 4.
3. При установившемся технологическом процессе в день в среднем происходит 10 обрывов нити на 100 веретенах. Определить вероятность того, что на 800 веретенах произойдет:
а) ровно 78 обрывов нити;
б) обрыв нити произойдет не более чем на 100 веретенах.
Решение:
р = 0,1, тогда q = 1 – p = 1 – 0,1 = 0,9


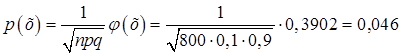
б) По интегральной формуле Лапласа


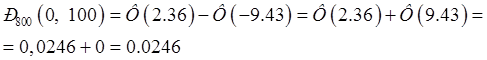
4. Участник олимпиады отвечает на 3 вопроса с вероятностью ответа на каждый соответственно 0,6, 0,7, 0,4.
За каждый верный ответ ему начисляется 5 баллов, за неверный списывается 5 балов. Составить закон распределения числа баллов, полученных участником олимпиады. Найти мат. ожидание этой случайной величины.
Решение:
Ряд распределения случайной величин X
(
числа баллов, полученных участником олимпиады)
| xi
|
-15
|
-5
|
5
|
15
|
| pi
|
0,4*0,3*0,6 =
= 0,072
|
0,6*0,3*0,6+0,4*0,7*0,6+0,4*0,3*0,6=0,312
|
0,6*0,7*0,6+0,4*0,7*0,4+0,6*0,3*0,4=0,436
|
0,6*0,7*0,4=0,168
|

5. Случайная величина Х подчинена нормальному закону распределения с нулевым математическим ожиданием. Вероятность попадания этой CD в интервал [-2, 2] равна 0,5705. Найти среднее квадратическое отклонение и плотность вероятности этой СВ.
Решение:
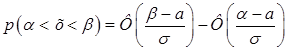



|