| КАФЕДРА МЕНЕДЖМЕНТА
КОНТРОЛЬНАЯ РАБОТА
По курсу: “Статистика"
Выполнил:
Проверил:
2007
Задача 1
На промышленном предприятии механическим способом отбора было обследовано 10% рабочих в количестве 30 человек. В результате обследования получены данные, приведенные в приложениях А, Б, В. С целью изучения зависимости между стажем работы рабочих, выработкой и качеством изготавливаемой продукции произвести аналитическую группировку по стажу работы, образовав три группы с интервалами до 3 лет, от 3 до 10, 10 и выше.
По каждой группе и по совокупности в целом подсчитать:
число рабочих;
количество произведенной продукции;
среднюю месячную выработку;
средний процент брака.
Результаты представить в виде таблицы, указать тип таблицы и сделать выводы о наличии связи между указанными признаками.
В качестве группировочного признака берем стаж рабочего.
После того, как выбран группировочный признак, намечено число групп и образованы сами группы, необходимо отобрать показатели, которые характеризуют группы, и определить их величины по каждой группе. Показатели, характеризующие рабочих, разносятся по трем вышеуказанным группам, и подсчитываются групповые итоги. Они заносятся в специально составленную таблицу (табл.1).
Таблица 1. - Вспомогательная таблица для построения аналитической группировки
| № рабочего
|
Стаж
|
Выработка
|
% брака
|
| Стаж до 3 лет
|
| 1
|
1
|
153
|
1,6
|
| 3
|
1
|
132
|
8,5
|
| 6
|
1
|
162
|
7,8
|
| 10
|
1
|
143
|
7,5
|
| ∑=4
|
-
|
590
|
25,4
|
| От 3 до 10 лет
|
| 2
|
4
|
168
|
6,2
|
| 4
|
9
|
124
|
19,5
|
| 5
|
3
|
171
|
6,1
|
| 7
|
8
|
125
|
13,0
|
| 8
|
3
|
102
|
7,0
|
| 9
|
8
|
170
|
5,8
|
| ∑=6
|
-
|
860
|
79,9
|
| Свыше 10 лет
|
| -
|
-
|
-
|
-
|
| Итого по таблице 10
|
-
|
3324
|
-
|
На основании данных табл.1 построим аналитическую группировку (табл.2).
Таблица 2. - Связь между стажем работы рабочих, выработкой и качеством продукции
| Группы рабочих по стажу, лет
|
Число рабочих
|
Изготовлено продукции, шт.
|
Процент брака
|
| Всего по группе
|
Одним рабочим
|
Всего по группе
|
Одного рабочего
|
| А
|
1
|
2
|
3
|
4
|
5
|
| До 3 лет
|
4
|
590
|
147,5
|
25,4
|
4,23
|
| От 3 до 10 лет
|
6
|
860
|
143,3
|
79,9
|
13,32
|
| свыше 10
|
0
|
-
|
-
|
-
|
-
|
| всего
|
10
|
1450
|
145
|
271,2
|
-
|
Примечание.
Графа 3=графа 2: графа 1; графа 5=графа 4: графа1
Вывод. Данная таблица является аналитической, так как выявляет взаимосвязь между признаками. Факторный признак-стаж (графа А). Результативные признаки: выработка (графа 3) и процент брака на одного рабочего (графа 5). На основании данных граф А и 3 можно сделать вывод, что связи между стажем и выработкой нет. Отсутствует также связь между стажем и процентом брака (графы А и 5).
По построению подлежащего (графа А) таблица является групповой. По разработке сказуемого - сложной (графы 1-5).
Задача 2
По исходным данным приложений Б и В построить интервальный вариационный ряд распределения с равновеликими интервалами. Результаты вычислений представить в виде таблицы.
Изобразить ряд распределения графически, построив гистограмму, полигон и кумуляту распределения.
РЕШЕНИЕ:
Для построения интервального ряда распределения с равновеликими интервалами по выработке выполним следующие действия:
Выберем минимальное значение выработки x min
=102 шт.;
Выберем максимальное значение x max
=171 шт.;
Определим размах совокупности: R= x max
- x min
= 171-102=69.
Определим число интервальных групп по формуле: m = √n
где n- объем совокупности (n=10).
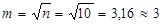
Определим величину интервала
d= R/m = 69/3 = 23
Построим интервалы по следующему алгоритму:
Первый интервал равен 102- (102+23) = 102-125;
Второй интервал равен 125- (125+23) = 125-148;
Третий интервал равен 148- (148+23) = 148-171.
По каждой интервальной группе подсчитаем число рабочих с заданными признаками.
Результаты представим в виде табл.3.
Таблица 3. - Распределение рабочих по выработке
| Группы рабочих по выработке, шт. (Х)
|
Число рабочих (f)
|
Накопленная частота (S)
|
| 102-125
|
2
|
2
|
| 125-148
|
2
|
4
|
| 148-171
|
6
|
10
|
| итого
|
10
|
-
|
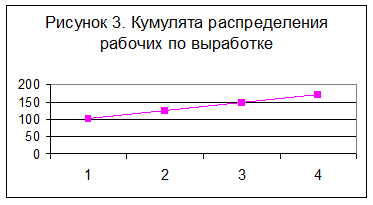
Изобразим графически полученный ряд распределения (рис.1-3).


Задача 3
На основании полученного ряда распределения в задаче 2 определить среднюю выработку, моду и медиану. Изобразите графически моду и медиану. Сделайте выводы.
РЕШЕНИЕ:
1. Расчет средней выработки.
Среднюю величину в интервальном ряду распределения рассчитывают по формуле средней арифметической взвешенной:
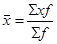
где х - середины интервалов;
f - частота.
Расчет необходимых данных выполним в табл.4.
Таблица 4. - Расчет данных для определения средней и дисперсии
| Группы рабочих по выработке, шт.
|
Число рабочих (f)
|
Середины интервалов (х)
|
х f
|
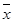 
x −
|
 (х-) 2 (х-) 2
|
 (х-) 2
∙f (х-) 2
∙f
|
| 102-125
|
2
|
113,5
|
227
|
-32,2
|
1036,84
|
2073,68
|
| 125-148
|
2
|
136,5
|
273
|
-9,2
|
84,64
|
169,28
|
| 148-171
|
6
|
159,5
|
957
|
13,8
|
190,44
|
1142,64
|
| итого
|
10
|
-
|
1457
|
-
|
-
|
3385,6
|
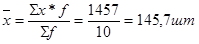
2. Мода (Мо) - значение признака, повторяющееся с наибольшей частотой. В интервальном ряду распределения мода определяется следующим образом:
Находим модальный интервал, которому соответствует наибольшая частота. В данной задаче модальными интервалом будет интервалы [148-171], так как ему соответствует наибольшая частота (6).
Внутри модального интервала мода определяется по формуле:
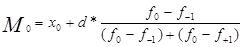
где х0 -
нижняя граница модального интервала;
f0 -
частота модального интервала;
f -1
- частота интервала, предшествующего модальному;
f+1
- частота интервала, следующего за модальным.
На основании данной формулы и табл.4 определим модальные значения средней выработки.
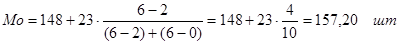
Вывод:
У большинства рабочих данной совокупности выработка составляет 157,20 шт. в месяц.
Медианой называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Для определения медианы в интервальном ряду сначала необходимо определить медианный интервал. Им считается тот, до которого сумма (накопленный итог) численностей меньше половины всей численности ряда, а с прибавлением его численности - больше половины. На основании данных табл.3 определим накопленные итоги (графа 3 табл.3). Половина численности ряда равна 5 (10: 2). Таким образом, третий интервал является медианным, так как накопленный итог предшествующего интервала меньше 5 (4<5), а накопленный итог 3-го интервала больше 5 (10>5).
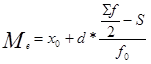
Внутри медианного интервала медиана определяется по формуле:
где х0 -
нижняя граница медианного интервала;
d - величина медианного интервала;
Sf - численность ряда (сумма частот);
S - накопленные итоги численностей до медианного интервала;
f0 -
численность медианного интервала.
Ме = 125+23× (2-4) /2= 102 шт.
Вывод:
50% рабочих данной совокупности имеют выработку до 102 шт., а вторая половина рабочих - выше 102 шт.
Задача 4
По результатам вычислений задач 2, 3 вычислить дисперсию, среднее квадратическое отклонение и коэффициент вариации. Поясните смысл полученных характеристик вариации.
РЕШЕНИЕ:
Дисперсия-это средний квадрат отклонения.
Расчет дисперсии для всей совокупности, представленной в виде сгруппированного ряда в табл.4, осуществляется по формуле:
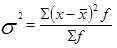
где х - середины интервалов;
Расчет данных для вычисления дисперсии выполним в табл.4.
σ2
= 3385,6: 10= 338,5

Среднее квадратическое отклонение определяется по формуле:

Коэффициент вариации определяется по формуле:

Коэффициент вариации меньше 33%, следовательно, совокупность является однородной, а средняя - типичной и устойчивой.
На основании аналитической группировки задачи 1 вычислить общую, межгрупповую и среднюю из внутригрупповых дисперсий. Определите корреляционное отношение по выработке одного рабочего. Сделайте выводы.
РЕШЕНИЕ:
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию и рассчитывается по формуле:
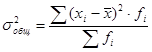
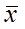 где - общая средняя по всей совокупности. где - общая средняя по всей совокупности.
Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:
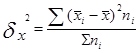
Где - средние по отдельным группам;
nj
-численности по отдельным группам.
Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:

Средняя из внутригрупповых дисперсий:
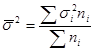
Закон, связывающий три вида дисперсий: общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
σ2
общ
= δ2
+ σ2
Данное соотношение называют правилом сложения дисперсий.
Для решения задачи сначала определим средние по каждой группе. Расчет средних выполнен в табл.5.
Средняя выработка в первой группе (до 3 лет) равна
х1
= 134,2 шт. (971: 5), во второй (от 3 до 10 лет) х2
= 127,0625 шт. (2033: 16), в третьей (свыше 10 лет) х3
= 142,667 шт. (1284: 9)
Промежуточные расчеты дисперсий по группам представлены в табл.5.
Таблица 5. - Расчет данных для определения внутригрупповых дисперсий.
| № рабочего
|
Выработка (х)
|
|
|
| 1
|
2
|
3
|
4
|
| До 3 лет
|
| 1
|
153
|
5,5
|
30,25
|
| 3
|
132
|
-15,5
|
240,25
|
| 6
|
162
|
14,5
|
210,25
|
| 10
|
143
|
-4,5
|
20,25
|
| Итого: 5
|
590
|
-
|
501,00
|
| От 3 до 10 лет
|
| 2
|
168
|
24,67
|
608,4
|
| 4
|
124
|
-19,33
|
373,8
|
| 5
|
171
|
27,67
|
765,4
|
| 7
|
125
|
-18,33
|
336,1
|
| 8
|
102
|
-41,33
|
1708,4
|
| 9
|
170
|
26,67
|
711,1
|
| Итого: 6
|
860
|
-
|
4503,3
|
| свыше 10 лет
|
| -
|
-
|
-
|
-
|
| Итого: 10
|
1450
|
-
|
5004,3
|
Подставив полученные значения в формулу, получим:
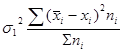
= (501 × 4) /10 = 200,4

= (4503,3 × 6) /10 = 2701,98
Средняя из групповых дисперсий:
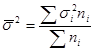
= (200,4 ×4+2701,98×6): 10 = (801,6 + 16211,88) / 10 = 1701,348
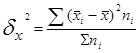
= [ (147,5-145) 2
×4+ (143,3 -145) 2
×6]: 10 = (25 + 17,34) /10= 4,234
Затем рассчитаем межгрупповую дисперсию. Средняя (общая) по всей совокупности равна 132,93 шт. (см. табл.2).
Таким образом, общая дисперсия согласно правилу сложения дисперсий:
σ2
общ
2
=δ2
+ σ2
=1701,348+4,234 = 1705,582
На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результативным признаками, который называется корреляционным отношением:
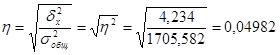
Величина 0,04982 показывает отсутствие связи между группировочным и результативным признаками.
Коэффициент детерминации η2
равен:
η2
=0,049822
= 0,0024820324 или 0,2482%
Он показывает, что вариация выработки на 0,2482% зависит от стажа и на 99,7518% (100% - 0,2482%) от других неучтенных факторов.
Задача 6
По исходным данным задачи 2 и результатам вычислений задачи 3, 4 установите:
с вероятностью 0,954 возможные пределы средней выработки в генеральной совокупности;
с вероятностью 0,997 возможные пределы удельного веса численности рабочих, имеющих выработку выше средней;
сколько необходимо отобрать рабочих, чтобы с вероятностью 99,7% предельная относительная ошибка выборки не превышала 5%?
РЕШЕНИЕ:
Средняя ошибка выборки определяется по формуле:
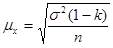
где k-коэффициент выборочного наблюдения (по условию задачи 10% или 0,1)
Предельная ошибка выборки определяется по формуле:,
где t - коэффициент доверия (для вероятности 0,954 равен 2)
Определим предельную ошибку средней выработки:
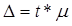
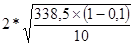 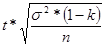
Δ х
= = = 11,04 шт.
Найдем границы изменения средней величины в генеральной совокупности:
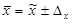 
145,7 -11,04< <145,7+11,04; 134,66 < <156,74
Вывод:
С вероятностью 0,954 можно утверждать, что средняя выработка одного Рабочего в генеральной совокупности находится в пределах от 134,66 шт.д.о 156,74 шт. (не ниже 134,66 шт., но не выше 156,74 шт)
2. Определим удельный вес рабочих, у которых выработка выше средней (145,7 шт.). Таких рабочих 5 человек. Тогда удельный вес их в общей численности составит:
W = 5/10 = 0,5
Рассчитаем предельную ошибку доли в случае механического отбора по формуле:

где w-удельный вес рабочих, у которых выработка выше средней;
n-объем выборочной совокупности;
t - коэффициент доверия (t=3 для вероятности 0,997).
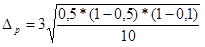
=3•0,15=0,45 или 45%
Найдем границы изменения доли в генеральной совокупности:
p=w±Δp
p=0,5±0,45
0,5-0,45<Р<0,5+0,45;
0,05 <Р< 0,95
5%<Р<95%
Вывод:
С вероятностью 0,997 можно утверждать, что удельный вес рабочих, у которых выработка выше средней, колеблется от 5% до 95%. В генеральной совокупности.
3. Рассчитаем необходимую численность рабочих:
n= (t2
•Vσ
2
): Δ2,
t- коэффициент доверия (для вероятности 99,7% равен 3);
Vσ
- коэффициент вариации (12,627% - результат решения задачи 4);
Δ2
- относительная погрешность, %; (по условию задачи равна 5%).
n=9• (12,627) 2
/25=57,399 ≈ 58 чел.
С вероятностью 99,7% можно утверждать, что численность выборки, обеспечивающая относительную погрешность не более 5%, должна составлять не менее 58 чел.
Задача 7
Имеются данные о стаже работы рабочих и их выработке (приложения А, графа *, Б-графа *).
Составьте линейное уравнение регрессии, вычислите его параметры, рассчитайте коэффициенты корреляции и эластичности. По полученному уравнению регрессии рассчитайте теоретические (выравненные) уровни. Результаты расчетов оформите в виде таблицы. Сделайте выводы.
РЕШЕНИЕ:
Уравнение связи в случае линейной зависимости имеет вид:
ух
=а0
+а1
х
Параметры уравнения а0
и а1
определяют методом наименьших квадратов. Для этого необходимо решить систему уравнений:
 na0
+a1
∑x=∑y; na0
+a1
∑x=∑y;
a0
∑x+ a1
∑x2
=∑xy.
Расчет необходимых данных выполним в табл.6
Подставим полученные данные в систему уравнений:
 10а0
+39а1
=1450 10а0
+39а1
=1450
39а0
+247а1
=5557
а0
=149,02741; а1
= - 1,03267
Уравнение связи между стажем и выработкой имеет вид:
ух
= 149,02741 - 1,03267х
Таблица 6. - Расчет данных для уравнения регрессии
| Х
|
У
|
Х2
|
ХУ
|
У2
|
Ух
|
| 1
|
153
|
1
|
153
|
23409
|
42,7
|
| 4
|
168
|
16
|
672
|
28224
|
98,8
|
| 1
|
132
|
1
|
132
|
17424
|
42,7
|
| 9
|
124
|
81
|
1116
|
15376
|
192,4
|
| 3
|
171
|
9
|
513
|
29241
|
80,1
|
| 1
|
162
|
1
|
162
|
26244
|
42,7
|
| 8
|
125
|
64
|
1000
|
15625
|
173,7
|
| 3
|
102
|
9
|
306
|
10404
|
80,1
|
| 8
|
170
|
64
|
1360
|
28900
|
173,7
|
| 1
|
143
|
1
|
143
|
20449
|
42,7
|
| Итого 39
|
1450
|
247
|
5557
|
215296
|
970
|
Интерпретация полученного уравнения связи:
Коэффициент регрессии а1
= - 1,03267, следовательно, связь между стажем и выработкой в данной совокупности обратная: при увеличении стажа на 1 год выработка снижается на 1,03267 шт.
Степень тесноты связи в случае линейной зависимости определяется с помощью линейного коэффициента корреляции:

где ∑xy: n = 5557: 10 = 555,7; 9,27; 150,67;
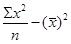
σ2
= = 247/10 - (9,27) 2
= 61,2329
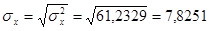
= 215296/10 - (150,67) 2
= 1171,8489;
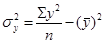
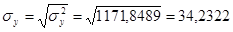
Коэффициент корреляции равен:
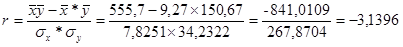
Коэффициент корреляции равен -3,1396.
Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак при увеличении факторного признака на 1%.
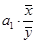
Э = 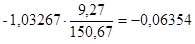
При увеличении стажа на 1% выработка снижается на 0,06354%.
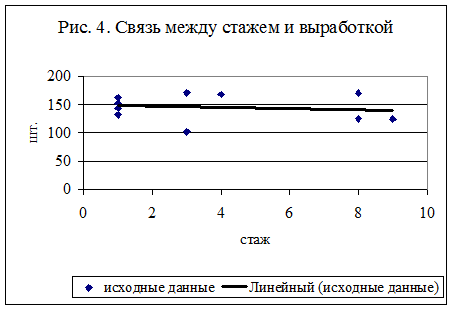
Графическое изображение связи - рис.4.
На основании данных в приложении Г проанализировать ряд динамики, исчислив:
абсолютные приросты, темпы роста и прироста по месяцам и к первому месяцу;
абсолютное содержание 1% прироста;
средний уровень ряда;
среднегодовой темп роста и прироста.
Результаты отразить в таблице. Изобразить ряд динамики графически. Сделать выводы.
РЕШЕНИЕ:
Поскольку в данном нам динамическом ряду каждый уровень характеризует явление за определенный отрезок времени, то такой ряд динамики называется интервальным.
Для расчета цепного абсолютного прироста используем формулу:
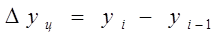
Δy февраль-январь
=412-365= 47; Δy март-февраль
=346-412 = - 66; Δy апрель-март
=405-346 = 59
и т.д.
Результаты запишем в гр.3 табл.7.
Для расчета базисного прироста используем формулу
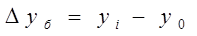
где у0
- уровень периода, принятого за базу сравнения
Δy февраль-январь
=412-365=47; Δy март-январь
=346-365=-19; Δy апрель-январь
=405-365=40 и т.д.
Результаты запишем в гр.4 табл.7.
2. Темп роста Тр представляет собой отношение текущего уровня уі
к предшествующему уровню у і-1
или базисному у1
. В первом случае абсолютный прирост называется цепным и рассчитывается по формуле 3, во втором -базисным и рассчитывается по формуле 4.

Тр= (3)
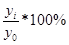
Тр= (4)
Темп роста цепной:
Тр февраль-январь
=412×100%: 365=112,9%; Тр март-февраль
=346×100%: 412=84,0%
Тр апрель-март
=405×100: 346=117,1% и т.д.
Результаты запишем в гр.5 табл.6.
Темп роста базисный:
Тр февраль-январь
=412×100%: 365=112,9%; Тр март-январь
=346×100%: 365=94,8%
Тр апрель-январь
=405×100: 365=111,0% и т.д.
Результаты запишем в гр.6 табл.7.
3. Темп прироста равен отношению абсолютного цепного или базисного прироста к предшествующему или базисному уровню. В первом случае называется цепным, во втором - базисным. Темп прироста рассчитывается по формуле 5:
Тпр = Тр%
- 100 (5)
Темп прироста цепной:
Тпр февраль-январь
=112,9%-100%=12,9%; Тпр март-февраль
=84,0%-100%=-16%;
Тр апрель-март
=117,1% -100%=17,1% и т.д.
Результаты запишем в гр.7 табл.7.
Темп прироста базисный:
Тр февраль-январь
=112,9%-100%=12,9%; Тр март-январь
=94,8%-100%=-5,2%;
Тр апрель-январь
=111%-100%=11,0% и т.д.
Результаты запишем в гр.8 табл.7.
4. Абсолютное содержание 1% прироста определяется как отношение цепного абсолютного прироста к темпу прироста и рассчитывается по формуле 6:
α= 0,01*уі-1 (
6).
α февраль
= 0,01×365=3,65; α март
= 0,01×412=4,12; α апрель
= 0,01×346=3,46 и т.д.
Результаты запишем в гр.9 табл.7.
Таблица 7. - Динамика реализации творога на рынках города в 2001 г. (тыс. кг)
| Меся-цы
|
Объем реализации, тыс. кг
|
Абсолютный прирост, млн. т
|
Темп роста,%
|
Темп прироста,%
|
Абсолют-ное содержа-ние 1% прироста, млн. т
|
| Цепной
|
Базисный
|
Цепной
|
Базисный
|
Цепной
|
Базисный
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| 1
|
365
|
-
|
-
|
-
|
100
|
-
|
-
|
-
|
| 2
|
412
|
47
|
47
|
112,9%
|
112,9%
|
12,9%
|
12,9%
|
3,65
|
| 3
|
346
|
-66
|
-19
|
84,0%
|
94,8%
|
-16,0%
|
-5,2%
|
4,12
|
| 4
|
405
|
59
|
40
|
117,1%
|
111,0%
|
17,1%
|
11,0%
|
3,46
|
| 5
|
475
|
70
|
110
|
117,3%
|
130,1%
|
17,3%
|
30,1%
|
4,05
|
| 6
|
504
|
29
|
139
|
106,1%
|
138,1%
|
6,1%
|
38,1%
|
4,75
|
| 7
|
407
|
-97
|
42
|
80,8%
|
111,5%
|
-19,2%
|
11,5%
|
5,04
|
| 8
|
367
|
-40
|
2
|
90,2%
|
100,5%
|
-9,8%
|
0,5%
|
4,07
|
| 9
|
448
|
81
|
83
|
122,1%
|
122,7%
|
22,1%
|
22,7%
|
3,67
|
| 10
|
443
|
-5
|
78
|
98,9%
|
121,4%
|
-1,1%
|
21,4%
|
4,48
|
| 11
|
415
|
-28
|
50
|
93,7%
|
113,7%
|
-6,3%
|
13,7%
|
4,43
|
| 12
|
379
|
-36
|
14
|
91,3%
|
103,8%
|
-8,7%
|
3,8%
|
4,15
|
| Итого
|
4966
|
14
|
-
|
-
|
-
|
-
|
-
|
-
|
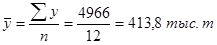
Средний уровень ряда:
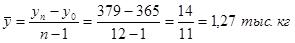
Средний абсолютный прирост:
Средний темп роста:

Средний темп прироста:
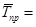 100,344% -100%= 0,344% 100,344% -100%= 0,344%
Вывод:
На основании табл.7 можно сделать выводы о том, что в 2001 г. среднемесячный объем реализации творога на рынках города составил 413,8 тыс. кг. Ежемесячно этот показатель в среднем увеличивался на 1,27 тыс. кг или на 0,344%.
Изобразим графически ряд динамики на рис.5.
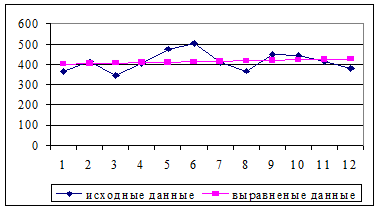
Используя данные задачи 8, произведите: аналитическое выравнивание ряда динамики по прямой.
РЕШЕНИЕ:
Осуществим аналитическое выравнивание для выражения основной тенденции по прямой. В случае линейной зависимости уравнение прямой имеет вид:
yt
=а0
+а1
t,
где а0
, а1
- параметры уравнения;
t - параметр времени.
Определим параметры уравнения методом наименьших квадратов. Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров а0, а1
:
 n а0
+ а1
Σt =Σy n а0
+ а1
Σt =Σy
а0
Σt+ а1
Σt2
= Σyt
Параметру t придаем для удобства расчетов такое значение, чтобы Σt=0.
Тогда:
а0
= Σy: n= 4966: 12=413,83;
а1
= Σyt: Σt2
= 659: 576= 1,144
Расчет данных выполним в табл.8.
Уравнение тенденции имеет вид:
уt
=413,83+1,144t
Подставим в полученное уравнение вместо параметра t его значения и вычислим теоретические значения уровней ряда динамики. Результаты вычислений запишем в гр.6 табл.8
Таблица 8
Расчет данных для выравнивания по прямой
| Месяц
|
Объем отправленного груза, млн. т (У)
|
t
|
t2
|
yt
|
Yt
|
| 1
|
2
|
3
|
4
|
5
|
6
|
| 1
|
365
|
-11
|
121
|
-4015
|
401,246
|
| 2
|
412
|
-9
|
81
|
-3708
|
403,534
|
| 3
|
346
|
-7
|
49
|
-2422
|
405,822
|
| 4
|
405
|
-5
|
25
|
-2025
|
408,11
|
| 5
|
475
|
-3
|
9
|
-1425
|
410,398
|
| 6
|
504
|
-1
|
1
|
-504
|
412,686
|
| 7
|
407
|
1
|
1
|
407
|
414,974
|
| 8
|
367
|
3
|
9
|
1101
|
417,262
|
| 9
|
448
|
5
|
25
|
2240
|
419,55
|
| 10
|
443
|
7
|
49
|
3101
|
421,838
|
| 11
|
415
|
9
|
81
|
3735
|
424,126
|
| 12
|
379
|
11
|
121
|
4169
|
426,414
|
| итого
|
4966
|
0
|
576
|
659
|
4971,96
|
Задача 10
Имеются данные о производстве изделий и себестоимости единицы изделия на промышленном предприятии за два месяца.
Исчислить:
Индивидуальные индексы физического объема, себестоимости и затрат.
Общие индексы физического объема продукции, себестоимости и затрат. Проверьте взаимосвязь общих индексов. Проанализируйте полученные результаты.
Размер абсолютного и относительного изменения затрат на производство за счет изменения себестоимости единицы продукции и физического объема.
РЕШЕНИЕ:
Определяем индивидуальные индексы физического объема по формуле:
iq
=q1
: q0
Изделие А iq
=12890: 12589=1,02;
Изделие Б iq
=10894: 11921=0,91
Определяем индивидуальные индексы себестоимости по формуле:
iz
=z1
: z0
Изделие А iz
=0,6: 0,57=1,05; Изделие Б iz
=0,68: 0,65=1,05
Определяем индивидуальные индексы затрат по формуле:
izq
= z1
q1
: z0
q0
Изделие А izq
= 0,57×12589: 0,6×12890=0,9282;
Изделие Б izq
=0,65×11921: 0,68×10894=1,0460
Взаимосвязь между индексами: izq
=iq
× iz
Изделие А izq
=0,9282 или 92,82%;
Изделие Б izq
=1,0460 или 104,60%
Таким образом, по изделию А затраты снизились на 7,18% (izq
=92,82). Вследствие повышения себестоимости единицы продукции произошло повышение затрат на 5,0% (izq
=1,05). По изделию Б затраты также увеличились на 5,0% (izq
=105,0%), в том числе в результате снижения физического объема - на 9% (izq
=91%), в результате роста себестоимости единицы продукции затраты выросли на 5,0% (izq
=105,0).
Таблица 8. - Динамика затрат на производство за два месяца по изделиям А и Б
| Изделие
|
Количество, шт.
|
Себестоимость, грн
|
Затраты на производство, грн
|
| Март
|
Апрель
|
Март
|
Апрель
|
Март
|
Апрель
|
условные
|
| q0
|
q1
|
z0
|
z1
|
zo
qo
|
z1
q1
|
z0
q1
|
| А
|
12589
|
12890
|
0,57
|
0,6
|
7175,73
|
7734
|
7347,3
|
| Б
|
11921
|
10894
|
0,65
|
0,68
|
7748,65
|
7407,92
|
7081,1
|
| итого
|
24510
|
23784
|
-
|
--
|
14924,4
|
15141,9
|
14428,4
|
4. Сводный индекс себестоимости рассчитывается по формуле:

где z0
- себестоимость единицы изделия за базисный период;
z1
- себестоимость единицы изделия за отчетный период;
q1
- количество изделий в отчетном периоде
Iz
=15141,9: 14428,4 = 1,0495 или 104,95%
Сводный индекс себестоимости показывает, что затраты на производство продукции в апреле по сравнению с мартом в результате роста себестоимости единицы продукции возросли на 4,95% (104,95%-100%).
5. Сводный индекс физического объема затрат рассчитывается по формуле:
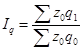
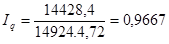
или 96,67%.
В результате снижения физического объема продукции затраты уменьшились на
3,33% (96,67%-100%)
6. Сводный индекс затрат на производство:
 =15141,9: 14924,4=1,0146 или 101,46% =15141,9: 14924,4=1,0146 или 101,46%
Общие затраты на производство всей продукции увеличились на
1,46% (101,46%-100%).
Общие индексы затрат, себестоимости и физического объема связаны между собой следующей зависимостью:
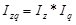 =1,0495×0,9667=1,0146 =1,0495×0,9667=1,0146
где Iя
q
- общий индекс затрат;
Iя
- общий индекс себестоимости;
Iq
- общий индекс физического объема.
7. Перерасход затрат в результате роста себестоимости единицы изделия составил:
Пz
=∑z1
q1
-∑z0
q1
=15141,9-14428,4= +713,52 грн.
Снижение затрат в результате уменьшения физического объема производства составило:
Сq
=∑z0
q1
-∑z0
q0
=14924,4-14428,4=+495,98 грн.
Общее снижение затрат составило:
Соб
=∑z1
q1
-∑z0
q0
= 15141,9--14924,4=+217,54 грн
Взаимосвязь показателей: общее увеличение затрат равно сумме перерасхода затрат от роста себестоимости единицы продукции и увеличение затрат в результате увеличения физического объема производства:
+713,52 =+495,98+217,54 грн.
Список литературы
1. Дэвид М. Левин, Дэвид Стефан, Тимоти С. Кребиль, Марк Л. Беренсон. Статистика для менеджеров с использованием Microsoft Office Excel - 2005 г., 1312 с.
2. Р.В. Фещур, А.Ф. Барвінський, В.П. Кічор. Статистика: теоретичні засади і прикладні аспекти. Навчальний посібник..3-е вид. перероблене і доповнене. - Львів: "Інтелект-Захід", 2006. - 256 с.
3. Методологические положения по статистике. Вып.5. Издательство: М., Статистика России, 2006, 510 c.
4. Статистика: показатели и методы анализа (справочное пособие). Издательство: Минск, Современная школа, 2005, 628 c.
5. Тюрин Ю., Макаров А. и др. Теория вероятностей и статистика (учебное пособие). Издательство: М., МЦНМО, Московские учебники, 2004, 256 c.
6. Лагутин М.Б. - Наглядная математическая статистика. Книга 1. 2003 г., 256 с.
7. Чернова Т.В. Экономическая статистика: Учебное пособие. Таганрог: Изд-во ТРТУ, 1999.140 с.
8. Захарченко Н.И. Бизнес-статистика и прогнозирование в Microsoft Office Excel. Самоучитель. 2004 г., 208 с.
9. Эндрю Сигел. Практическая бизнес-статистика.4-е издание. 2007 г. .1057
|