| Череповецкий военный инженерный институт радиоэлектроники.
Кафедра №8
Курсовая работа по математике
Тема: «Частотно-временной анализ сигналов»
Выполнили:
Плотников Е.А.
г. Череповец-2008.
Содержание
1. Плоскость частота-время
2. Базисные функции частотно-временного анализа
3. Прямое и обратное преобразование Фурье
4. Дискретное вейвлет-преобразование
4.1 Дискретизация масштаба
4.2 Дискретизация масштаба и сдвига. Фреймы
4.3 Примеры дискретного вейвлет-преобразования
Литература
1. Плоскость частота-время
Для анализа и сравнения частотно-временных локализационных свойств различных базисов используют плоскость частота-время. Любая функция  может характеризоваться интервалом It
на временной оси и интервалом может характеризоваться интервалом It
на временной оси и интервалом 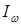 в Фурье области, в которых содержится 90% ее энергии, сосредоточенной около центра тяжести функции в Фурье области, в которых содержится 90% ее энергии, сосредоточенной около центра тяжести функции Тогда в этой плоскости функцию Тогда в этой плоскости функцию можно изобразить в виде прямоугольника, как показано на рис. 3.1. можно изобразить в виде прямоугольника, как показано на рис. 3.1.

Очевидно, что смещение функции на 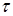 от исходного состояния вызовет перемещение прямоугольника параллельно оси t. Модуляция этой функции комплексной экспонентой от исходного состояния вызовет перемещение прямоугольника параллельно оси t. Модуляция этой функции комплексной экспонентой 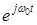 сдвигает прямоугольник параллельно оси сдвигает прямоугольник параллельно оси  (рис.3.2.). (рис.3.2.).

Масштабирование функции (ее сжатие или растяжение) приводит к развороту прямоугольника. Действительно, получим новую функцию масштабированием функции масштабированием функции  на коэффициент a: на коэффициент a:
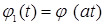
Энергия такой функции E:

Следовательно, ширина функции  равна равна 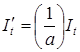 . В соответствии со свойством масштабирования Фурье-преобразования ( . В соответствии со свойством масштабирования Фурье-преобразования ( ) ) 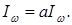 Влияние масштабирования на положение функции в плоскости время-частота показано на рис. 3.3. Влияние масштабирования на положение функции в плоскости время-частота показано на рис. 3.3.

В качестве примеров функций, иллюстрирующих эффективность их представления в плоскости время-частота, рассмотрим 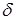 функцию Дирака и Фурье - базис. Известно, что функцию Дирака и Фурье - базис. Известно, что 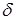 - функция является идеальным базисом для временного анализа сигналов. Результатом такого анализа являются отсчеты, которые можно рассматривать как временной спектр сигнала. На плоскости время - частота - функция является идеальным базисом для временного анализа сигналов. Результатом такого анализа являются отсчеты, которые можно рассматривать как временной спектр сигнала. На плоскости время - частота 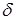 функция функция 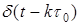 выглядит как показано на рис. 3.4а, т.е. эта функция обладает свойством хорошей временной локализации, но плохой локализацией в спектральной области (она имеет равномерный спектр на всех частотах). Базисные функции выглядит как показано на рис. 3.4а, т.е. эта функция обладает свойством хорошей временной локализации, но плохой локализацией в спектральной области (она имеет равномерный спектр на всех частотах). Базисные функции Фурье-анализа, наоборот, обладают хорошей частотной локализацией в то время, как во временной области они имеют бесконечную протяженность (см. рис. 3.4б). Фурье-анализа, наоборот, обладают хорошей частотной локализацией в то время, как во временной области они имеют бесконечную протяженность (см. рис. 3.4б).

2. Базисные функции частотно-временного анализа
Итак, частотно-временной анализ предназначен для выявления локальных частотно-временных возмущений сигнала. Вследствие кратковременности таких возмущений, сам сигнал может рассматриваться как заданный в L2
т.е. для одномерных сигналов – на всей действительной оси  с нормой с нормой 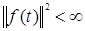 . Следовательно, базисные функции, которые получили название вейвлетов, также должны принадлежать L2
и быстро убывать при . Следовательно, базисные функции, которые получили название вейвлетов, также должны принадлежать L2
и быстро убывать при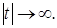 Тогда, чтобы перекрыть такими базисными функциями все возможные временные положения сигнала, необходимо, чтобы базисные функции представляли собой набор смещенных во времени функций. Удобнее всего, если этот набор образуется из одной и той же "материнской" функции Тогда, чтобы перекрыть такими базисными функциями все возможные временные положения сигнала, необходимо, чтобы базисные функции представляли собой набор смещенных во времени функций. Удобнее всего, если этот набор образуется из одной и той же "материнской" функции  (прототипа), сдвинутой по оси t т.е. (прототипа), сдвинутой по оси t т.е.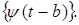 Чтобы обеспечить частотный анализ, базисная функция должна иметь еще один аргумент – масштабный коэффициент, который является аналогом частоты в Фурье-анализе. Тогда базисные функции для частотно-временного анализа будут иметь вид Чтобы обеспечить частотный анализ, базисная функция должна иметь еще один аргумент – масштабный коэффициент, который является аналогом частоты в Фурье-анализе. Тогда базисные функции для частотно-временного анализа будут иметь вид

Где масштабный коэффициент  введен как делитель t, причем масштабированию подвергается также и сдвиг b. Это позволяет сохранить относительную "плотность" расположения базисных функций по оси t при расширении или сжатии самой функции и при введен как делитель t, причем масштабированию подвергается также и сдвиг b. Это позволяет сохранить относительную "плотность" расположения базисных функций по оси t при расширении или сжатии самой функции и при  (рис 3.6) (рис 3.6)

Таким образом, базисные функции для частотно-временного анализа должны обладать следующими свойствами. Ограниченность
, т.е. принадлежность L2 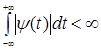 . Локализация
. Базисные функции вейвлет - анализа, в отличие от преобразования Фурье, должны быть локализованы, т.е. определены на конечном интервале как во временной, так и в частотной областях. Для этого достаточно, чтобы выполнялись условия:
. Локализация
. Базисные функции вейвлет - анализа, в отличие от преобразования Фурье, должны быть локализованы, т.е. определены на конечном интервале как во временной, так и в частотной областях. Для этого достаточно, чтобы выполнялись условия:
 
Нулевое среднее.
Равенство нулю нулевого момента
или, что иногда необходимо – равенство нулю момента m-го порядка

Это – вейвлеты m-го порядка, позволяющие анализировать более тонкую структуру сигнала, подавляя медленно изменяющиеся его составляющие.
3. Прямое и обратное преобразование Фурье
При 
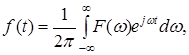
- прямое преобразование Фурье

- обратное преобразование Фурье.
Комплексная функция имеет смысл спектральной плотности, ее иногда называют непрерывным спектром Фурье-функции f(t). имеет смысл спектральной плотности, ее иногда называют непрерывным спектром Фурье-функции f(t).
Также как и в случае периодической функции, предполагается, что f(t) удовлетворяет условиям Дирихле или, что эквивалентно, абсолютно интегрируема и удовлетворяет условию Дини.
Отметим также, что:

4. Дискретное вейвлет-преобразование
Представление функции f(t) через ее непрерывное вейвлет – преобразование является избыточным. В задачах обработки информации, встречающихся на практике, сигнал, во-первых, имеет ограниченную полосу и, во-вторых, допускаются те или иные погрешности в получаемых результатах. Поэтому используют дискретное представление непрерывных сигналов, при которых параметры преобразования, в данном случае a и b, приобретают дискретные значения. Вейвлет-преобразование, при котором значения a и b дискретны, называют дискретным вейвлет-преобразованием (DWT - Discrete Wavelet Transform).
4.1 Дискретизация масштаба
Рассмотрим сначала случай дискретного масштаба a и положим 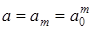 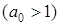 . Это равноценно разбиению частотной оси на поддиапазоны (частотные полосы). Предположим, что . Это равноценно разбиению частотной оси на поддиапазоны (частотные полосы). Предположим, что 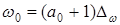 (это можно сделать всегда, умножив функцию ψ на некоторый модуляционный множитель (это можно сделать всегда, умножив функцию ψ на некоторый модуляционный множитель 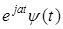 (см. (см. ). Тогда частотное окно будет равно: ). Тогда частотное окно будет равно:

а центральная частота m-го вейвлета:
 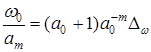 . .
Базисом для DWT является функция, полученная из
(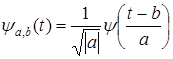 ) )
при 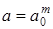 : :
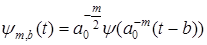 . .
Если справедливо  и если и если 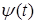 достаточно быстро затухает, то любая функция из L2
может быть представлена в виде дискретной по достаточно быстро затухает, то любая функция из L2
может быть представлена в виде дискретной по 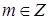 последовательности последовательности
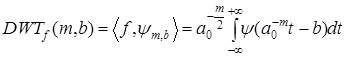 (3.5.2.) (3.5.2.)
Для восстановления f(t) по дискретным значениям (3.5.2.) на базис 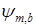 (t) налагаются дополнительные ограничения, а именно, образ Фурье вейвлета (t) налагаются дополнительные ограничения, а именно, образ Фурье вейвлета 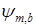 (t) должен удовлетворять соотношению (t) должен удовлетворять соотношению
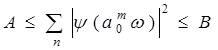 , (3.5.3) , (3.5.3)
где константы А и В такие, что 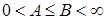 . Условие (3.5.3.) в терминах радиотехники имеет довольно прозрачное толкование. Действительно, так как при каждом значении масштаба . Условие (3.5.3.) в терминах радиотехники имеет довольно прозрачное толкование. Действительно, так как при каждом значении масштаба 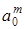 вейвлет представляет собой полосовой фильтр, то набор (сумма) этих фильтров (блок фильтров) является некоторым устройством с неравномерной частотной характеристикой, определяемой константами A и B (рис. 3.12). Сигнал, например звуковой, на выходе такого устройства при сильной неравномерности частотной характеристики претерпевает существенные искажения. Поэтому для его восстановления принимают специальные меры, в частности, устанавливают фильтр, компенсирующий искажения частотной характеристики. В вейвлет-преобразовании таким фильтром является дуальный (или двойственный) вейвлет вейвлет представляет собой полосовой фильтр, то набор (сумма) этих фильтров (блок фильтров) является некоторым устройством с неравномерной частотной характеристикой, определяемой константами A и B (рис. 3.12). Сигнал, например звуковой, на выходе такого устройства при сильной неравномерности частотной характеристики претерпевает существенные искажения. Поэтому для его восстановления принимают специальные меры, в частности, устанавливают фильтр, компенсирующий искажения частотной характеристики. В вейвлет-преобразовании таким фильтром является дуальный (или двойственный) вейвлет 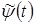 , Фурье-образ которого имеет вид: , Фурье-образ которого имеет вид:
 . (3.5.4.). . (3.5.4.).

Покажем, что с помощью такого вейвлета по коэффициентам DWT полностью восстанавливается сигнал. Действительно, используя соотношение Парсеваля
(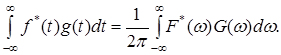 ) )
и формулу получим (3.5.4.):

Из (3.5.4.) и (3.5.3.) можно показать, что
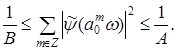
4.2 Дискретизация масштаба и сдвига. Фреймы
В этом случае полагают дискретными величины a и b, т.е.  Частотное окно для анализа сохраняется прежним. Ширина временного окна Частотное окно для анализа сохраняется прежним. Ширина временного окна

равна  , а среднее значение , а среднее значение 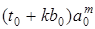 изменяется дискретно пропорционально m -ой степени a0
- масштабу вейвлета. Чем уже функция ψ, т.е. меньше величина изменяется дискретно пропорционально m -ой степени a0
- масштабу вейвлета. Чем уже функция ψ, т.е. меньше величина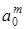 , тем меньше (на ту же величину) шаг сдвига этой функции. Базисными функциями для дискретного вейвлет-преобразования будут функции, получаемые из , тем меньше (на ту же величину) шаг сдвига этой функции. Базисными функциями для дискретного вейвлет-преобразования будут функции, получаемые из  ,при ,при  и и 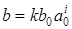

Коэффициенты разложения любой функции из L2
могут быть получены как

Выражение (3.5.6) является дискретным вейвлет-преобразованием функции  . Чтобы обратное преобразование во временную область было справедливым, должно выполняться следующее условие: . Чтобы обратное преобразование во временную область было справедливым, должно выполняться следующее условие:

для всех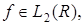 если константы A и B такие, что если константы A и B такие, что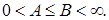 В этом случае формула для восстановления функции f(t) по коэффициентам В этом случае формула для восстановления функции f(t) по коэффициентам будет иметь вид будет иметь вид
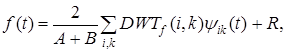 (3.5.8) (3.5.8)
где ошибку восстановления R можно оценить как  Разделив все члены неравенства (3.5.7) на Разделив все члены неравенства (3.5.7) на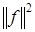 , можно видеть, что константы A и B являются границами нормированной на , можно видеть, что константы A и B являются границами нормированной на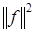 энергии – скалярного произведения энергии – скалярного произведения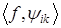 . Они (эти константы) как бы "обрамляют" нормированную энергию коэффициентов . Они (эти константы) как бы "обрамляют" нормированную энергию коэффициентов Отсюда произошел термин фрейм (frame), которым называют множество функций Отсюда произошел термин фрейм (frame), которым называют множество функций 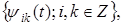 при которых условие (3.5.7) выполняется. Если A= B , то при которых условие (3.5.7) выполняется. Если A= B , то и множество и множество 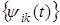 называют плотным фреймом. При этом выражение называют плотным фреймом. При этом выражение  вытекающее из (3.5.7), является обобщением теоремы Парсеваля на плотные фреймы. Для плотных фреймов из (3.5.8) получаем вытекающее из (3.5.7), является обобщением теоремы Парсеваля на плотные фреймы. Для плотных фреймов из (3.5.8) получаем

Если A=B=1, то плотный фрейм становится ортогональным базисом. Заметим, что для вейвлетов, образованных материнским вейвлетом (3.3.6), хорошие результаты при восстановлении сигналов получаются при 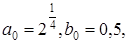 так как так как 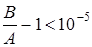 . Для больших величин, например . Для больших величин, например 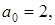 будет будет 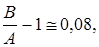 т.е. восстановление приводит к большим искажениям. т.е. восстановление приводит к большим искажениям.
4.3 Примеры вейвлетов для дискретного преобразования
Как было отмечено выше, функции вейвлет обладают свойством частотно-временной локализации, т.е. они ограничены как в частотной, так и во временной областях. Ниже рассмотрим два примера: первый – спектр вейвлетов в частотной области представляет собой идеальный полосовой фильтр, второй – сами функции вейвлет представляют собой прямоугольники. Все вейвлеты, с точки зрения частотно-временных свойств, занимают промежуточное положение между этими крайними случаями.
Sinc-базис. Разобьем ось частот на интервалы (поддиапазоны), как показано на рис. 3.13 при a0
= 2. Такое разбиение называют логарифмическим, так как отношение верхней и нижней границ диапазонов постоянно и равно 2. Такое разбиение является еще и идеальным, так как оно реализуется идеальными полосовыми фильтрами. Подобная идеализация нужна для исследования свойств частотного разложения с помощью идеализированных вейвлетов, что позволит в дальнейшем перейти к более сложным разложениям. Любой сигнал 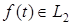 со спектром со спектром может занимать полосу частот, охватывающую несколько таких поддиапазонов. может занимать полосу частот, охватывающую несколько таких поддиапазонов.

Тогда  и и 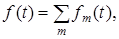 т.е. сигнал представляет собой сумму некоторого числа элементарных сигналов. В рассматриваемом идеальном случае частотные каналы не перекрываются, поэтому имеет место ортогональность этих элементарных сигналов, т.е. т.е. сигнал представляет собой сумму некоторого числа элементарных сигналов. В рассматриваемом идеальном случае частотные каналы не перекрываются, поэтому имеет место ортогональность этих элементарных сигналов, т.е.

Выберем из всего множества сигналов такие, которые ограничены полосой частот 2I
, т.е. имеющие спектр 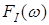 . Рассмотрим периодическую функцию . Рассмотрим периодическую функцию 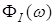 такую, что: такую, что:  , т.е. полученную периодизацией F1
(ω) (рис. 3.14) , т.е. полученную периодизацией F1
(ω) (рис. 3.14)

Тогда спектр функции: Fi
(ω) при произвольном I можно представить в виде:

Где 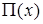 - функция окна такая, что: - функция окна такая, что:

Посмотрим, как при этих условиях можно представить функцию f (t) во временной области. Для этого разложим периодическую функцию 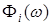 с периодом с периодом  , в ряд Фурье (см. , в ряд Фурье (см.  ): ):


Где, подставляя (3.5.10а) в (3.5.9) и выполняя обратное преобразование Фурье, получим:

Вычислим первый интеграл. Переставляя операции суммирования и интегрирования и ограничивая пределы интегрирования с учетом функции окна, получим:
 
где вейвлет
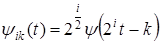 (3.5.14) (3.5.14)
и (см. рис. 3.16):
 (3.5.15) (3.5.15)
Выражение (3.5.13) является представлением функции f (t) в базисе вейвлет. В рассматриваемом частном случае идеальной полосовой фильтрации вейвлетом является функция (3.5.14), образованная из материнской функции  по (3.5.15) с учетом (3.5.12). Такой вейвлет называется sinc –вейвлетом по имени функции (3.5.12), которая его образует, а функция (3.5.12) получила название масштабной функции. по (3.5.15) с учетом (3.5.12). Такой вейвлет называется sinc –вейвлетом по имени функции (3.5.12), которая его образует, а функция (3.5.12) получила название масштабной функции.

Множитель при при  необходим для сохранения нормы необходим для сохранения нормы 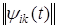 вне зависимости от величины масштаба, так как: вне зависимости от величины масштаба, так как:

Покажем, что в рассматриваемом частном случае 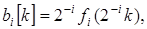 т.е. определяется отсчетами функции т.е. определяется отсчетами функции  при при 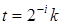 . Рассмотрим интеграл Фурье ( . Рассмотрим интеграл Фурье ( ) при дискретных значениях ) при дискретных значениях 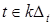 функции функции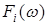 , заданной на интервале , заданной на интервале 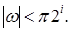 Имеем, с учетом (3.5.10б): Имеем, с учетом (3.5.10б):

Последнее равенство справедливо при 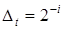 и вещественных и вещественных 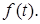
Следовательно,
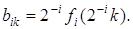
Выполнив преобразование Фурье выражения (3.5.14), можно видеть, что спектр Фурье sinc -вейвлета представляет собой идеальный полосовой фильтр, в общем случае занимающий полосу частот от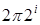 до до 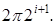
Вейвлет Хаара. Разобьем теперь временную ось на интервалы, как показано на рис. 3.17 и определим на единичном интервале функцию

Эта функция является материнским вейвлетом, так как она удовлетворяет условию (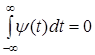 ). Система сдвигов таких функций ). Система сдвигов таких функций 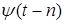 образует ортонормальный базис, так как их взаимная энергия равна нулю при образует ортонормальный базис, так как их взаимная энергия равна нулю при  и равна единице при и равна единице при 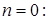

Преобразование Фурье ( ) вейвлета Хаара имеет вид и показано на рис. 3.17б. ) вейвлета Хаара имеет вид и показано на рис. 3.17б.


Функции Хаара, также как sinc -вейвлет, могут быть получены с помощью масштабной функции

что иллюстрируется на рис. 3.18.

Из приведенных примеров следует ряд интересных выводов:
1. Представление вейвлет-функции в виде прямоугольников в любой из областей (частотной или временной) ведет к бесконечному расширению в противоположной области. Следовательно, для того, чтобы функции вейвлет были локализованы одновременно во временной и частотной областях, они должны убывать с ростом аргумента, по крайней мере, по закону обратной пропорциональности (см.(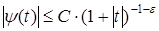 и и 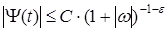 )). )).
2. Вейвлеты ψ(t), спектры Фурье которых представляют собой полосовые фильтры, могут быть выражены через масштабные функции 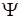 (t), спектры Фурье которых представляют собой фильтры нижних частот (см. формулы (3.5.15) и (3.5.19)). (t), спектры Фурье которых представляют собой фильтры нижних частот (см. формулы (3.5.15) и (3.5.19)).
3. Базисные функции для DWT могут быть получены из одной материнской функции путем ее масштабирования и сдвига (см. формулы (3.5.14) и (3.5.15)).
4. Любой сигнал f(t) из L2
может быть представлен своим вейвлет- разложением (3.5.13), если число компонентов fi
(t) таково, что они занимают полосу частот большую, чем полоса сигнала.
Литература
1. Новиков И.Я., Стечкин СБ. Основы теории всплесков // Успехи математических наук. 1998. V. 53. № 6. С.9-13.
2.Петухов А.П. Введение в теорию базисов всплесков. СПб.: Изд. СПбГТУ, 1999. 131 с.
3.Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет-преобразования. СПб.: ВУС, 1999. 203 с.
4. Астафьева Н.М. Вейвлет-анализ: основы теории и примеры применения// УФН . 1996. Т. 166, № 11. С. 1145-1170.
5. Martin Vatterli, Jelena Kovačevic. Wavelets and Subband Coding. Prentice Hall, New Jersey, 1995.
|