| Содержание
Введение
1. Биография А. Гурвица
2. Вспомогательные определения
3. Теорема Ферма
4. Вопрос Гурвица
5. Теорема Гурвица
6. Приложение теоремы Гурвица
Заключение
Список используемой литературы
Введение
Предметом исследования данной курсовой работы являются различные системы «чисел», которые можно построить, исходя из действительных чисел, путем добавления рядя «мнимых единиц». Классический пример такой системы – это система комплексных чисел.
Одно из важнейших свойств комплексных чисел выражается тождеством 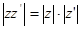 . Если обозначить . Если обозначить 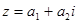 , ,  , то данное тождество перепишется в виде , то данное тождество перепишется в виде 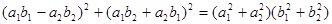 . прочитанное справа налево это тождество звучит так: «Произведение суммы двух квадратов на сумму двух квадратов есть снова сумма двух квадратов». . прочитанное справа налево это тождество звучит так: «Произведение суммы двух квадратов на сумму двух квадратов есть снова сумма двух квадратов».
Существуют ли подобные тождества с большим, чем 2, числом квадратов? Как описать такие тождества?
Цель моей курсовой работы ответить на эти вопросы. Вопросы совсем не простые; в течение многих лет занимали умы математиков. Исчерпывающий ответ был получен в XIX веке немецким математиком А.Гурвицем. Он сформулировал интересную теорему, доказательство которой будет проведено позже.
1. Биография А. Гурвица
Адольф Гурвиц (26 марта 1859, Хильдесхайм — 18 ноября 1919, Цюрих) — немецкий математик. Родился в семье с еврейскими корнями. Его отец, Соломон Гурвиц, работал в машиностроительной отрасли; мать Эльза умерла, когда Адольфу было всего три года.
В гимназии, куда он поступил в 1868 году, ему преподавал математику Герман Шуберт. Заметив и оценив талант в юном Адольфе, Шуберт убедил его отца помочь сыну с получением дальнейшего образования в университете.
Гурвиц поступил в университет Мюнхена в 1877 году. В течение первого года обучения он посещал лекции Феликса Клейна. Адольф Гурвиц обладал исключительным математическим талантом. Вот что написал профессор Ф.Клейн отцу Адольфа о будущем его сына накануне защиты Гурвицем диссертации: «Прежде всего, я хочу подчеркнуть, что с тех пор, как я тут работаю, я не встречал молодого человека, который мог бы сравниться по специфическому математическому таланту с Вашим сыном. Ему, без сомнения, уготована блестящая научная карьера, уверенность в которой подкрепляется тем фактом, что его дар счастливо сочетается с замечательными человеческими чертами. Единственной опасностью остается его здоровье. Вероятно, Ваш сын уже давно ослаб из-за чрезмерного напряжения в его занятиях. Позвольте мне заверить Вас, что никто не будет так счастлив, как я, если здоровье Вашего сына полностью восстановится. Мне необходима его бескомпромиссная поддержка в моих последних исследованиях»
. [2]
Через год Гурвиц переезжает в Берлин, где в местном университете посещает лекции Куммера, Кронекера, Вейерштрасса. Заканчивает обучение в Лейпциге (1880).
Преподавательскую карьеру начал в Кёнигсбергском университете, где в 1884 году стал профессором. В этом же году женился на Иде Самуэль, у них было трое детей.
С 1892 года А. Гурвиц - профессор Политехнической школы в Цюрихе. Среди его студентов в Цюрихе были Давид Гильберт и Альберт Эйнштейн.
Его основные труды — по математическому анализу, теории функций, алгебре и теории чисел. В теории функций комплексного переменного известны теоремы Гурвица. Широкое применение нашел его критерий отрицательности действительных частей корней алгебраических уравнений (критерий Гурвица). Сделал также значительный вклад в геометрию. Гурвиц написал классическую двухтомную монографию по теории аналитических и эллиптических функций. Одним из первых он глубоко исследовал римановы многообразия и их приложения к теории алгебраических кривых. Решил изопериметрическую проблему.
В 1898 году Гурвиц поставил такую задачу: описать все тройки натуральных чисел (r,s,n), для которых возможна формула вида:
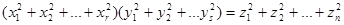
В этой формуле все 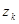 - билинейные комбинации переменных - билинейные комбинации переменных 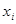 и и  . Примеры формул такого вида можно получить, исходя из правила умножения комплексных чисел, кватернионов или октав. Задача Гурвица открыта до сих пор, хотя многие выдающиеся математики пытались ее решить, и созданный ими топологический аппарат (характеристические классы, вещественная К-теория) оказался полезным во многих других областях математики. Сам Гурвиц и, независимо, Радон, полностью описали случай s = n=r. . Примеры формул такого вида можно получить, исходя из правила умножения комплексных чисел, кватернионов или октав. Задача Гурвица открыта до сих пор, хотя многие выдающиеся математики пытались ее решить, и созданный ими топологический аппарат (характеристические классы, вещественная К-теория) оказался полезным во многих других областях математики. Сам Гурвиц и, независимо, Радон, полностью описали случай s = n=r.
2. Вспомогательные определения
Комплексные числа-
числа вида х + iy, где х и у — действительные числа, а i — так называемая мнимая единица (число, квадрат которого равен —1); х называют действительной частью, а у — мнимой частью.
Размерность пространства:
векторное пространство 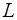 над полем F называется над полем F называется 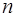 -мерным
, если в нем существуют -мерным
, если в нем существуют 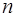 линейно независимых векторов, а любые линейно независимых векторов, а любые 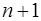 векторов уже являются линейно зависимыми. При этом число векторов уже являются линейно зависимыми. При этом число 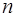 называется размерностью
пространства называется размерностью
пространства 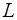 . Размерность пространства . Размерность пространства 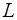 обычно обозначают символом обычно обозначают символом  . .
n
-мерное Евклидово пространство над полем
F
:
Вещественное векторное пространство 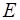 называется вещественным евклидовым пространством
(или просто евклидовым пространством), если выполнены следующие два требования: называется вещественным евклидовым пространством
(или просто евклидовым пространством), если выполнены следующие два требования:
Имеется правило, посредством которого любым двум элементам этого пространства 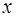 и и 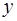 ставится в соответствие вещественное число, называемое скалярным произведением
этих элементов (и обозначаемое символом ставится в соответствие вещественное число, называемое скалярным произведением
этих элементов (и обозначаемое символом 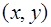 ). ).
Указанное правило подчинено следующим четырем аксиомам:
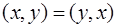 (коммутативность или симметрия); (коммутативность или симметрия);
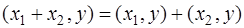 (дистрибутивность скалярного произведения относительно сложения); (дистрибутивность скалярного произведения относительно сложения);
 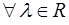 ; ;
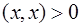 , если , если  ; ; 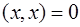 , если , если 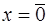 . .
Подпространство-
такое подмножество пространства L, которое само является пространством.
Ортонормированный базис:
Говорят, что 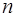 элементов элементов 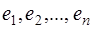 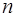 -мерного евклидова пространства -мерного евклидова пространства 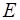 образуют ортонормированный базис
этого пространства, если эти элементы попарно ортогональны и норма каждого из них равна единице, т.е. если образуют ортонормированный базис
этого пространства, если эти элементы попарно ортогональны и норма каждого из них равна единице, т.е. если
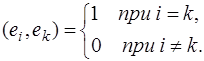
Билинейное отображение:
Пусть L-линейное пространство над полем Р. Тогда отображение 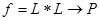 называется билинейным, если называется билинейным, если
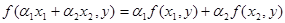 , , 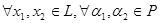
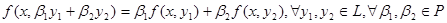
Сюръективное отображение-
отображение 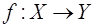 , которое каждому элементу из , которое каждому элементу из 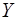 сопоставляет, по крайней мере, один прообраз, т.е. сопоставляет, по крайней мере, один прообраз, т.е. 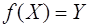 . .
Ядро:
Пусть 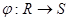 - гомоморфизм кольца R в кольцо S. Множество - гомоморфизм кольца R в кольцо S. Множество 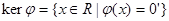 , где 0’-нуль в S, -ядро. , где 0’-нуль в S, -ядро.
Обратимая матрица-
матрица, для которой существует обратная матрица.
Невырожденная матрица -
квадратная матрица, определитель которой отличен от нуля.
Симметричная матрица
- матрица является симметричной, если она совпадает со своей транспонированной матрицей (т.е. A = A'). Другими словами, нижний треугольник квадратной матрицы является "зеркальным отражением" верхнего треугольника.
Характеристика поля
- пусть P-поле. Если существует такое целое положительное n, что для каждого 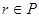 выполняется равенство n·r=0, то наименьшее из таких чисел n называется характеристикой поля P. Обозначение - char P. выполняется равенство n·r=0, то наименьшее из таких чисел n называется характеристикой поля P. Обозначение - char P.
Кососимметричная матрица-
квадратная матрица А над полем P характеристики 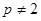 такая, что такая, что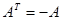 , где , где 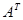 — транспонированная матрица. — транспонированная матрица.
Линейная независимость системы векторов:
Система векторов 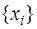 называется линейно независимой
, если существует только тривиальная линейная комбинация данных векторов равная нулевому вектору. называется линейно независимой
, если существует только тривиальная линейная комбинация данных векторов равная нулевому вектору.
3. Теорема Ферма
Какие целые числа можно представить в виде суммы квадратов двух целых чисел? Это один из самых старых вопросов теории чисел, восходящий, по крайней мере, к Диофанту. Полный ответ на данный вопрос дал Пьер де Ферма (французский математик, 17 августа 1601 — 12 января 1665). Напишем первые несколько целых чисел, представимых в виде суммы квадратов
0;
1;
2;
4;
5;
8;
9;
10;
13;
16;
17;
18;
20;
25;
26;
29;
32;
34;
36;
37;
40;
41;
45;
49;
50;
52;
53;
58;
61;
64;
65;
68;
72;
73;
74;
80;
81;
82;
85;
89;
90;
97;
98;
100
Можно сделать несколько экспериментальных выводов. Во-первых, не каждое число представимо в виде суммы двух квадратов. Например, 3, 6, 11, 12 не представляются в таком виде. Более того, можно заметить, что ни одно число вида 4к+3 не представляются в виде суммы двух квадратов (при целом к). Во-вторых, если каждое из двух чисел является суммой квадратов, то таково и их произведение. Можно сделать и другие заключения.
Остановимся более детально на втором заключении и попробуем обосновать его. Справедлива формула
 (1) (1)
Действительно,
 и и 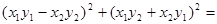

Из этой формулы, в частности, вытекает, что если каждое из чисел a и b можно представить как сумму квадратов двух целых чисел, то их произведение тоже представимо в таком виде. Формула (1) является простым следствием коммутативного, ассоциативного и дистрибутивного законов.
Формула (1) важна для теории чисел. В следующих разделах мы обсудим ее теоретико-числовые приложения, а также и другие аналогичные формулы, важные для теории чисел.
Теорема 1 (Ферма): Для того чтобы нечётное простое число было представимо в виде суммы двух квадратов, необходимо и достаточно, чтобы оно при делении на 4 давало в остатке 1.
Доказательство: Доказательство принадлежит Жозе́фу Луи́ Лагра́нжу (25 января 1736, Турин — 10 апреля 1813, Париж, французский математик).
Оно опирается на следующую лемму Вильсона: если p - простое число, то число (p-1)!+1 делится на p.
Чтобы не отвлекаться на доказательство этого вспомогательного факта, продемонстрируем лишь основную идею этого доказательства на примере простого числа 13. Для любого числа x: 2  x x  11, найдется такое число y: 2 11, найдется такое число y: 2 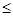 y y 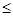 11, что x*y при делении на 13 дает в остатке 1. Действительно, (13-1)!=12!=(2* 7)(3* 9)(4* 10)(5* 8)(6* 11)* 12, и при этом все произведения в скобках при делении на 13 дают в остатке 1, а значит, 12! при делении на 13 даст в остатке 12, откуда (для выбранного нами числа 13) следует утверждение леммы Вильсона. Обобщение, приведенной выше идеи, приводит к доказательству леммы Вильсона и в общем случае. 11, что x*y при делении на 13 дает в остатке 1. Действительно, (13-1)!=12!=(2* 7)(3* 9)(4* 10)(5* 8)(6* 11)* 12, и при этом все произведения в скобках при делении на 13 дают в остатке 1, а значит, 12! при делении на 13 даст в остатке 12, откуда (для выбранного нами числа 13) следует утверждение леммы Вильсона. Обобщение, приведенной выше идеи, приводит к доказательству леммы Вильсона и в общем случае.
Из леммы Вильсона извлечем такое следствие: если p=4n+1, где n - натуральное число, то ((2n)!)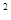 +1 делится на p. Действительно, из леммы Вильсона следует, что (4n)!+1 делится на p, и теперь необходимое утверждение вытекает из следующей выкладки: +1 делится на p. Действительно, из леммы Вильсона следует, что (4n)!+1 делится на p, и теперь необходимое утверждение вытекает из следующей выкладки:
(4n)!+1=(2n)!(2n+1)*...*(4n)+1=(2n)!(p-2n)(p-(2n-1))*...*(p-1)+1=(2n)!*
*(-1)2n
(2n)!+pk+1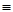 ((2n)!) ((2n)!)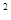 +1(mod p). +1(mod p).
Обозначим (2n)! через N. Мы доказали, что N2 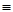 -1(mod p).
-1(mod p).
Теперь рассмотрим все пары целых чисел (m,s), такие что 0 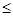 m m 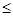 [ [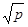 ], 0 ], 0 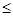 s s 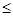 [ [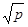 ], через [ ], через [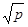 ] обозначена целая часть числа - наибольшее целое число, не превосходящее ] обозначена целая часть числа - наибольшее целое число, не превосходящее 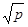 . Число таких пар ([ . Число таких пар ([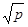 ]+1)>p2
. Значит, по крайней мере, для двух различных пар ( ]+1)>p2
. Значит, по крайней мере, для двух различных пар (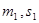 ) и ( ) и (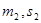 )остатки от деления )остатки от деления 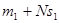 , , 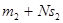 на p одинаковы, т. е. число a+Nb, где a=m
на p одинаковы, т. е. число a+Nb, где a=m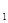 -m2
, b=s -m2
, b=s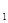 -s2
, будет делиться на p. При этом |a| -s2
, будет делиться на p. При этом |a|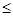 [ [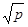 ], |b| ], |b| 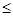 [ [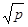 ]. Но тогда число a ]. Но тогда число a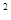 -N -N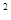 b b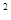 =(a+Nb)(a-Nb) делится на p, и значит, учитывая, что N2 =(a+Nb)(a-Nb) делится на p, и значит, учитывая, что N2
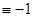 (mod p), получим, что a (mod p), получим, что a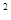 +b2
делится на p, т. е. a +b2
делится на p, т. е. a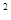 +b +b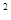 =rp где r - натуральное число (r =rp где r - натуральное число (r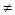 0, иначе пары были бы одинаковы). С другой стороны, a 0, иначе пары были бы одинаковы). С другой стороны, a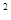 +b2 +b2 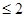 [
[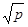 ] ]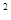 <2p, т. е. r=1, и значит, a <2p, т. е. r=1, и значит, a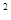 +b +b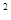 =p. Теорема доказана. =p. Теорема доказана.
Пример 1:
 , , 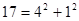 , , 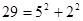 , , 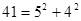 , , 
Вопрос о представлении чисел в виде суммы двух квадратов исчерпывается следующим утверждением: Для того чтобы целое рациональное число было представимо в виде суммы двух квадратов, необходимо и достаточно, чтобы простые числа вида 4n+3 входили в разложение этого числа на простые сомножители в четных степенях. [3]
4. Вопрос Гурвица
Вернемся к формулам с суммами квадратов. Теперь нас интересует такая алгебраическая задача: какие формулы с суммами квадратов можно написать для случая многих переменных? Сформулируем эту задачу более точно. Рассмотрим формулу вида
 (2), (2),
в которой все  - билинейные комбинации переменных - билинейные комбинации переменных  и и 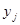 . Билинейные комбинации-выражения вида . Билинейные комбинации-выражения вида 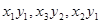 и т.д., а также суммы таких выражений, взятых с произвольными действительными коэффициентами. Формулу (2) будем называть формулой типа (r,s,n). и т.д., а также суммы таких выражений, взятых с произвольными действительными коэффициентами. Формулу (2) будем называть формулой типа (r,s,n).
Существует формула типа (4, 4, 4). Это связано со знаменитой алгеброй кватернионов, построенной Уильямом Роуэном Гамильтоном (1806—1865, ирландский математик).
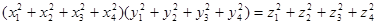 , где , где
 , ,
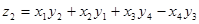 , ,
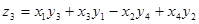
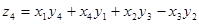 , ,
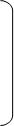  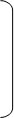  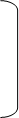  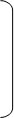  1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1
 0 -1 0 0 , 0 -1 0 0 , = 1 0 0 0 , = 1 0 0 0 , 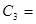 0 0 0 -1 , 0 0 0 -1 , 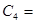 0 0 1 0 0 0 1 0
0 0 -1 0 0 0 0 1 1 0 0 0 0 -1 0 0
0 0 0 -1 0 0 -1 0 0 1 0 0 1 0 0 0
Комплексные числа удобно отождествлять с точками плоскости, поскольку они имеют две координаты – вещественную часть и мнимую. По аналогии с комплексными числами, Гамильтон долго пытался построить «трехмерные числа», т.е. наделить точки трехмерного пространства естественными операциями сложения и умножения, удовлетворяющими некоторым естественным свойствам. Однако, ему это не удалось. Более того, в некотором естественном смысле, таких «хороших» операций не существует. Все же поиски были не бесполезны. В результате своих поисков Гамильтон наткнулся на замечательную и естественную конструкцию «четырехмерных» чисел – кватернионов.
Кватернионом
называется выражение вида
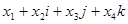 , ,
в котором i, j, k – формальные символы, не являющиеся действительными числами. Эти символы удовлетворяют следующим соотношениям:
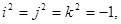 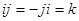 , , 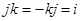 , , 
Первая серия соотношений состоит в том, что каждое из чисел i, j, k является мнимой единицей. Вторая серия соотношений содержит 2 вещи. Первая – мнимые единицы i, j, k антикоммутируют. Кроме этого, вторая серия соотношений выражает произведение любых двух мнимых единиц из трех указанных через эти же самые мнимые единицы. Как складывать и перемножать произвольные кватернионы? Для этого нужно воспользоваться правилами умножения мнимых единиц i, j, k, а также всеми обычными законами сложения и обычным законом дистрибутивности. Например,

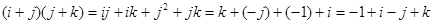
Теорема 2: Умножение кватернионов ассоциативно, т.е. для любых трех кватернионов 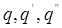 выполнено равенство выполнено равенство 
Кватернион 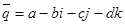 называется сопряжённым к называется сопряжённым к 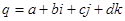 . .
Так же, как и для комплексных чисел,
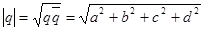
называется модулем q (или нормой q).
Теорема 3: Для любой пары кватернионов 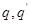 выполнено соотношение выполнено соотношение
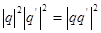
Доказательство:
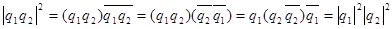
Эту формулу можно интерпретировать как формулу типа (4, 4, 4) для произведения сумм квадратов.
Формула типа (8, 8, 8) была найдена в 1845 году английским математиком А.Кэли.
А. Гурвиц в 1898 году поставил следующий вопрос, который до сих пор является открытым: Для каких целых чисел r, n, s существует формула типа (r, s, n) для произведения сумм квадратов?
Этот вопрос имеет несколько вариантов. В формуле типа (r, s, n) сумма квадратов r переменных, умноженная на сумму квадратов s переменных, представляется в виде суммы квадратов n билинейных форм от этих двух групп переменных. Однако коэффициенты в этих билинейных формах могут быть целыми, вещественными, комплексными и т.п. Ни в одной из этих ситуаций, на вопрос Гурвица не найдено полного ответа. Кажется, что ответ должен зависеть от выбора коэффициентов. Для всех известных примеров формул с комплексными коэффициентами, существуют формулы того же типа с вещественными и даже целыми коэффициентами.
5. Теорема Гурвица
Рассмотрим n-мерное Евклидово пространство  . Если . Если  , то его длиной называют число , то его длиной называют число  . Естественно поставить . Естественно поставить
Вопрос 1
. Для каких n существует билинейное отображение 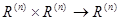 такое, что такое, что 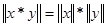 для любых для любых  ? ?
Заметим, что, если выполнено это условие 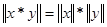 , то , то 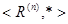 -алгебра без делителей нуля (т.к. -алгебра без делителей нуля (т.к. 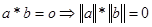 и либо а=0, либо b=0). Более того, если и либо а=0, либо b=0). Более того, если 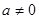 , то для любого и разрешимо уравнение , то для любого и разрешимо уравнение 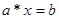 и и 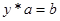 . Т.к. отображения . Т.к. отображения  и и 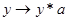 имеют нулевые ядра и следовательно являются сюръективными (т.е. имеют нулевые ядра и следовательно являются сюръективными (т.е.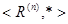 является телом, вообще говоря неассоциативным и некоммутативным). Если является телом, вообще говоря неассоциативным и некоммутативным). Если 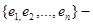 ортонормированный базис ортонормированный базис 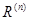 , то , то  и если и если 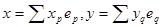 , то , то  , где , где 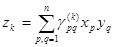 и условие и условие 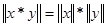 эквивалентно следующему вопросу. эквивалентно следующему вопросу.
Вопрос 2:
Для каких n существует тождество  , где , где  -любые действительные числа, -любые действительные числа, 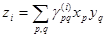 и матрицы и матрицы 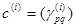 являются постоянными, т.е. не зависят от являются постоянными, т.е. не зависят от 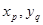 ? ?
В 1989 году Гурвиц доказал, что представлять произведение целых чисел в виде сумм квадратов целых чисел можно только для множителей, состоящих из сумм двух, четырех и восьми квадратов.
Теорема 4: Вопросы 1-2 имеют решение только при n=1,2,4,8.
Доказательство: Будем считать, что 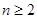 . Положим . Положим 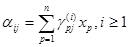 , ,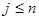 . Тогда равенство . Тогда равенство 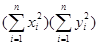 = =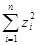 , где , где  переписывается в виде переписывается в виде
 = =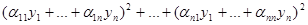 . .
Фиксируем 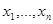 и рассмотрим левую и правую части многочлена от и рассмотрим левую и правую части многочлена от 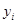 .Тогда .Тогда
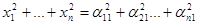 , ,
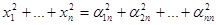
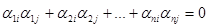 , ,
Если  , то предыдущие равенства равносильны , то предыдущие равенства равносильны 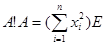 . Перепишем . Перепишем  , где , где 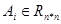 (т.е. (т.е. 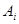 не зависит от не зависит от 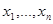 ). Тогда из равенства ). Тогда из равенства 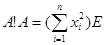 следует эквивалентное равенство следует эквивалентное равенство 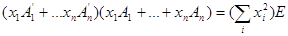 , сравнивая коэффициенты при , сравнивая коэффициенты при  , последнее влечет за собой , последнее влечет за собой  , i=1,2,..,n и ,следовательно, , i=1,2,..,n и ,следовательно, 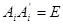 . Положим . Положим 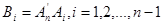 . Тогда предыдущее равенство можно переписать в виде: . Тогда предыдущее равенство можно переписать в виде:
 , , 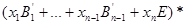
* . .
Сравнивая коэффициенты при  , получим, что , получим, что 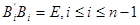 , , 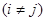 , ,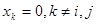 . Получим . Получим 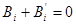 , , 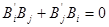 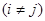 или или  , , 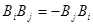 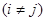 , , 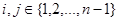 . Покажем, что существование таких матриц . Покажем, что существование таких матриц 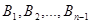 влечет за собой, что n=2,4,8. влечет за собой, что n=2,4,8.
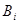 -кососимметричная и невырожденная. Значит n-четное число. В частности -кососимметричная и невырожденная. Значит n-четное число. В частности 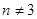
Породим этими матрицами подалгебру
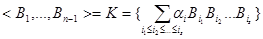
Матрица вида  , где , где  является системой K . Их число равно является системой K . Их число равно 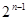 . Покажем, что, по меньшей мере, . Покажем, что, по меньшей мере, 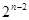 из них линейно независимы. Для этого сначала заметим, что из них линейно независимы. Для этого сначала заметим, что 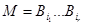 , ,  удовлетворяет удовлетворяет
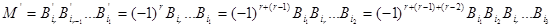 = =
=
В частности М - симметричная тогда и только тогда, когда 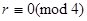 , либо , либо 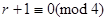 . Если существует соотношение . Если существует соотношение 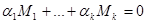 , где , где 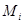 -слева от -слева от 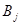 , то можно считать, что все , то можно считать, что все 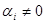 и все собственные подмножества и все собственные подмножества 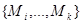 являются линейно независимыми. Тогда, умножая на являются линейно независимыми. Тогда, умножая на 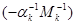 , получим соотношение вида: , получим соотношение вида:  . При этом все . При этом все 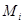 являются симметричными (ввиду линейной независимости являются симметричными (ввиду линейной независимости 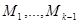 ). ).
Пусть 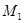 вовлекает наименьшее число факторов r . Тогда вовлекает наименьшее число факторов r . Тогда
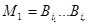 . .
Если  и и 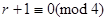 , то выберем , то выберем 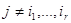 и умножим левую и правые части на и умножим левую и правые части на 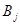 . Получим, что . Получим, что 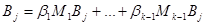 . Т.к. . Т.к. 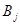 -кососимметричная, а -кососимметричная, а 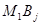 -симметричная, то получили противоречие. -симметричная, то получили противоречие.
Если  , то умножим обе части на , то умножим обе части на  . Получим, что . Получим, что 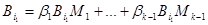 , где , где 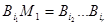 ( их количество 4e-1) – симметричная матрица, а слева кососимметричная матрица. Противоречие. Следовательно, ( их количество 4e-1) – симметричная матрица, а слева кососимметричная матрица. Противоречие. Следовательно, 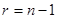 и и  , и как показывают рассуждения выше, либо , и как показывают рассуждения выше, либо 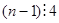 , либо , либо 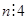 . Если . Если 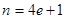 , то, умножая на , то, умножая на 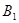 , получим, что , получим, что 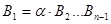 (их число n-2=4e-1) – симметричная. Противоречие. следовательно (их число n-2=4e-1) – симметричная. Противоречие. следовательно 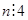 . В частности, если . В частности, если  и и 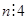 , то получаем противоречие, т.е. , то получаем противоречие, т.е. 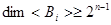 . Пусть . Пусть 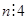 . Докажем, что . Докажем, что 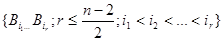 - линейно независимы. Их число равно - линейно независимы. Их число равно 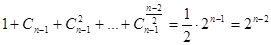 . Действительно, если между ними есть линейно зависимые, то получим, что . Действительно, если между ними есть линейно зависимые, то получим, что 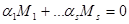 , где длина , где длина
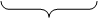  , , 
Длина
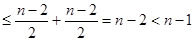
Т.е. мы не получили 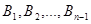 . Противоречие. . Противоречие.
Итак, 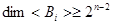 и и 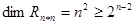 . Это возможно при . Это возможно при  . Если n<10, то при n=2,4,8 теорема верна. Далее n-четное число. Осталось понять, что при n=6 кососимметричные матрицы из . Если n<10, то при n=2,4,8 теорема верна. Далее n-четное число. Осталось понять, что при n=6 кососимметричные матрицы из  линейно независимы. линейно независимы.
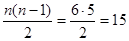 в в 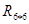 . .
С другой стороны, среди 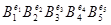 , где , где 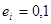 (их число равно 32) количество кососимметричных равно (их число равно 32) количество кососимметричных равно 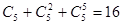 . Т.к. . Т.к. 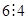 , то все эти матрицы , то все эти матрицы 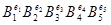 линейно независимы. В частности и эти линейно независимы линейно независимы. В частности и эти линейно независимы 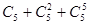 . С другой стороны их число меньше 15. Противоречие. (Можно сослаться что . С другой стороны их число меньше 15. Противоречие. (Можно сослаться что 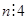 , 6-не подходит). , 6-не подходит).
Таким образом, теорема Гурвица доказана. [1]
Пример 2:
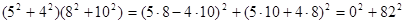
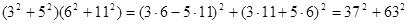 
Можно ответить на вопрос Гурвица в случае s=n. Это сделал сам Гурвиц в конце жизни, через 20 лет после того, как поставил свой вопрос. Ответ, оказывается, связан с представлениями алгебр Клиффорда. Ответ звучит так: формула типа (r, n, n) существует тогда и только тогда, когда число r не превосходит числа p, зависящего от n следующим образом. Пусть 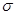 -наибольшая степень двойки, на которую делится число n. Разделим -наибольшая степень двойки, на которую делится число n. Разделим 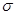 на 4 с остатком. Обозначим через a неполное частное, а через b остаток. Тогда на 4 с остатком. Обозначим через a неполное частное, а через b остаток. Тогда 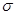 =4a+b, =4a+b, 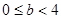 . Число p равно . Число p равно 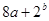 [5] [5]
6. Приложение теоремы Гурвица
В 1878 г. Немецкий математик Г. Фробениус доказал следующую замечательную теорему.
Теорема Фробениуса. Любая ассоциативная алгебра с делением изоморфна одной из трех: алгебре действительных чисел, алгебре комплексных чисел или алгебре кватернионов.
Впоследствии был установлен более общий результат, который можно назвать обобщенной теоремой Фробениуса.
Обобщенная теорема Фробениуса. Любая альтернативная алгебра с делением изоморфна одной из четырех алгебр: алгебре действительных чисел, алгебре комплексных чисел, алгебре кватернионов или алгебре октав.
Альтернативной алгеброй называется алгебра, в которой для любых двух элементов
a
,
b
справедливы равенства 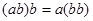 , ,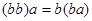 . .
Чтобы доказать эти теоремы, перечислим сначала некоторые свойства ассоциативной алгебры с делением.
Утверждение 1. Алгебра А содержит 1.
Утверждение 2. Если элемент 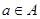 не пропорционален 1, то совокупность не пропорционален 1, то совокупность 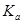 элементов вида элементов вида 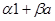 образует подалгебру, изоморфную алгебре комплексных чисел. образует подалгебру, изоморфную алгебре комплексных чисел.
Утверждение 3. Если элементы 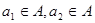 не принадлежат одной подалгебре не принадлежат одной подалгебре  , то совокупность , то совокупность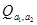 элементов вида элементов вида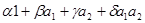 образует подалгебру, изоморфную алгебре кватернионов. образует подалгебру, изоморфную алгебре кватернионов.
Доказательство теоремы Фробениуса.
Дадим сначала другое определение альтернативной алгебры.
Пусть
a
,
b
–два произвольных элемента алгебра А. Рассмотрим всевозможные произведения, составленные из них. Если каждое такое произведение не зависит от способа расстановки скобок, алгебра А называется альтернативной.
При доказательстве теоремы будем использовать второе определение альтернативности, т.е. докажем следующую теорему: Если алгебра А с делением такова, что любое произведение, составленное из двух произвольных элементов a, b, не зависит от расстановки скобок, то алгебра А изоморфна одной из четырех алгебр: алгебре действительных чисел, алгебре комплексных чисел, алгебре кватернионов или алгебре октав.
Доказательство утверждения 1. Найдя элемент е из уравнения xa=a и умножив обе части равенства ea=a слева на е, получим e(ea)=ea или, учитывая ее альтернативность, (ee)a=ea. Отсюда следует, что ее=е. Опять-таки в силу альтернативности имеем (be)e=b(ee) и e(ec)=(ee)c, т.е. (be)e=be и e(ec)=ec. Отсюда следует be=b и ec=c. Значит е - единица алгебры.
Другие утверждения примем без доказательства.
Попытаемся доказать, что алгебра А является нормированной. Отсюда по теореме Гурвица будет следовать нужный нам результат.
Введем в алгебре А операцию сопряжения следующим образом. Если элемент а пропорционален 1, то 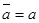 . Если же а не пропорционален 1, то, согласно утверждению 2, он содержится в комплексной подалгебре . Если же а не пропорционален 1, то, согласно утверждению 2, он содержится в комплексной подалгебре 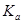 . В этой подалгебре для элемента а имеется сопряженный элемент . В этой подалгебре для элемента а имеется сопряженный элемент 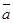 , который мы и примем за элемент, сопряженный к а в алгебре А. , который мы и примем за элемент, сопряженный к а в алгебре А.
Из определения 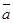 непосредственно вытекает непосредственно вытекает 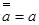 , а также , а также  , где , где 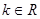 - любое. - любое.
Для вывода других свойств сопряжения нам необходимо выяснить один вопрос. Пусть элемент а не пропорционален 1. Рассмотрим какую-либо кватернионную подалгебру 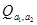 , содержащую а. В этой подалгебре для а тоже имеется сопряженный элемент , содержащую а. В этой подалгебре для а тоже имеется сопряженный элемент 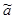 . Будет ли он совпадать с определенным выше элементом . Будет ли он совпадать с определенным выше элементом 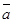 ? Покажем, что будет. ? Покажем, что будет.
Элементы а и 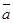 , как сопряженные в комплексной алгебре, удовлетворяют условиям , как сопряженные в комплексной алгебре, удовлетворяют условиям 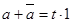 и и  , где t, p – действительные числа. , где t, p – действительные числа.
Элементы а и 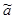 как сопряженные в алгебре кватернионов удовлетворяют аналогичным условиям: как сопряженные в алгебре кватернионов удовлетворяют аналогичным условиям: 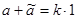 и и 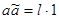 , где k, l – действительные числа. , где k, l – действительные числа.
Вычтем из последних равенств предыдущие, получим: 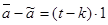 и и 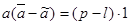 и если и если 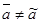 , то из этих соотношений вытекает, что элемент а пропорционален 1, что противоречит предположению. , то из этих соотношений вытекает, что элемент а пропорционален 1, что противоречит предположению.
Т.о., элемент, сопряженный а, один и тот же, независимо от того, рассматриваем ли мы а как элемент комплексной подалгебры  (т.е. как комплексное число) или же как элемент какой-либо подалгебры (т.е. как комплексное число) или же как элемент какой-либо подалгебры 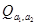 (т.е. как кватернион). (т.е. как кватернион).
Заметим попутно, что то же самое относится и к модулю элемента а. Поскольку 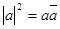 как в случае комплексных чисел, так и в случае кватернионов, то модуль элемента а не зависит от ого, рассматриваем ли мы а как элемент комплексной или же кватернионной подалгебры. как в случае комплексных чисел, так и в случае кватернионов, то модуль элемента а не зависит от ого, рассматриваем ли мы а как элемент комплексной или же кватернионной подалгебры.
Из того, что доказано нами относительно сопряжения, легко следует, что для любых двух элементов a и b алгебры А справедливы равенства
 , , 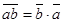
Действительно, если a и b принадлежат одной комплексной подалгебре (т.е. 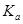 совпадает с совпадает с 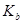 ), то написанные равенства суть свойства сопряжения в этой подалгебре; если же b не содержится в ), то написанные равенства суть свойства сопряжения в этой подалгебре; если же b не содержится в  , то эти равенства снова справедливы – уже как свойства сопряжения в , то эти равенства снова справедливы – уже как свойства сопряжения в 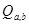 . .
Из 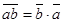 и из и из 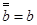 вытекает, что элемент, сопряженный вытекает, что элемент, сопряженный 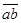 равен равен 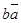 ; следовательно, ; следовательно, 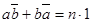 , n – действительное число. , n – действительное число.
Определим в алгебре А скалярное произведение (a, b) с помощью формулы 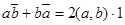 . Что выражение (a, b) обладает всеми свойствами скалярного произведения, проверяется просто. Напомним эти свойства: . Что выражение (a, b) обладает всеми свойствами скалярного произведения, проверяется просто. Напомним эти свойства:
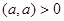 , если , если 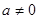 и (0,0)=0 и (0,0)=0
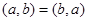
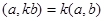
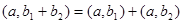
В данном случае свойство 2 очевидно, 2-е свойство вытекает из  , 3-е из , 3-е из 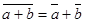 . Для доказательства 1-го свойства следует написать . Для доказательства 1-го свойства следует написать
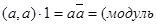 
и учесть, что модуль комплексного числа а строго положителен, если 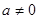 , и равен нулю, если а=0. , и равен нулю, если а=0.
Заметим, что из последнего равенства следует  , т.е. норма элемента а в алгебре А совпадает с модулем а как комплексного числа (или кватерниона). , т.е. норма элемента а в алгебре А совпадает с модулем а как комплексного числа (или кватерниона).
Т.к. любые 2 элемента a и b алгебры А принадлежат одной комплексной или одной кватернионной подалгебре, то 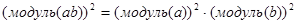 (ведь алгебра комплексных чисел, так же как и алгебра кватернионов, является нормированной), или (ab,ab)=(a,a)(b,b). Но это равенство как раз и означает нормированность алгебры А. Дальше вступает теорема Гурвица, согласно которой алгебра А изоморфна одной из четырех алгебр: действительных чисел, кватернионов, октав. В этом как раз и заключается обобщенная теорема Фробениуса.[7] (ведь алгебра комплексных чисел, так же как и алгебра кватернионов, является нормированной), или (ab,ab)=(a,a)(b,b). Но это равенство как раз и означает нормированность алгебры А. Дальше вступает теорема Гурвица, согласно которой алгебра А изоморфна одной из четырех алгебр: действительных чисел, кватернионов, октав. В этом как раз и заключается обобщенная теорема Фробениуса.[7]
Приведем еще одно применение теоремы Гурвица (или тождества Гамильтона).
Теорема Лагранжа.
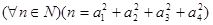 . .
Лемма. Для любого простого числа p>2 найдется число 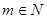 , такое что mp=a , такое что mp=a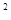 +b +b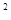 +c +c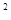 , a, b, c , a, b, c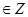 . .
Доказательство:
Рассмотрим два множества чисел:
K={0, 1, 4, ...,  }, L={-1-0, -1-1, -1-4, ..., -1- }, L={-1-0, -1-1, -1-4, ..., -1- }. }.
В каждом из множеств числа попарно несравнимы по модулю p. В самом деле, возьмем 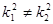 из множества K (или, эквивалентно, -1-k из множества K (или, эквивалентно, -1-k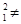 -1-k -1-k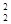 из множества L), где из множества L), где 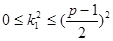 , , 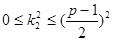 . Если k . Если k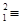 k k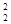 (mod p), то (k (mod p), то (k +k +k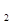 )(k )(k -k -k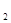 ) ) 0 (mod p). . Но 0< k 0 (mod p). . Но 0< k +k +k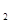 <p и 0<| k <p и 0<| k -k -k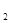 |<p, поскольку k |<p, поскольку k <p/2, k <p/2, k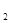 <p/2 и <p/2 и 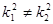 . Противоречие. . Противоречие.
Всего в этих двух множествах p+1 чисел, следовательно, среди них найдутся сравнимые по модулю p, т. е. такие числа 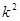 из первого множества и из первого множества и 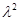 из второго, что из второго, что  . Откуда . Откуда 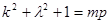 для некоторого для некоторого 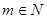 . Теперь, поскольку k<p/2, . Теперь, поскольку k<p/2, 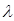 <p/2, получаем mp= <p/2, получаем mp=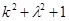 < <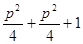 < <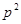 , а значит, m<p. Лемма доказана. , а значит, m<p. Лемма доказана.
Доказательство теоремы Лагранжа:
Докажем, что любое простое число представимо в виде суммы четырех квадратов целых чисел. Для p=2 имеем 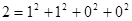 . Для p>2, по предыдущей лемме, найдется такое m<p, что число mp можно представить в виде mp= . Для p>2, по предыдущей лемме, найдется такое m<p, что число mp можно представить в виде mp=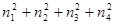 (n (n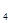 можно положить равным 0). Выберем теперь минимальное натуральное m, обладающее таким свойством. Покажем, что оно равно 1. Пусть m четно. Тогда либо все n можно положить равным 0). Выберем теперь минимальное натуральное m, обладающее таким свойством. Покажем, что оно равно 1. Пусть m четно. Тогда либо все n имеют одинаковую четность, либо среди них есть два четных и два нечетных (нумерация этих чисел не важна, поэтому пусть n имеют одинаковую четность, либо среди них есть два четных и два нечетных (нумерация этих чисел не важна, поэтому пусть n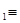 n n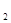 (mod 2), а n (mod 2), а n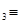 n n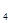 (mod 2). В обоих случаях числа (mod 2). В обоих случаях числа
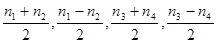 являются целыми. Имеем: являются целыми. Имеем:
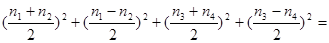 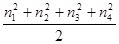 = = , ,
значит, 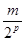 также представляется в виде суммы четырех квадратов целых чисел. Но также представляется в виде суммы четырех квадратов целых чисел. Но  , а m, по предположению, минимальное число с таким свойством. Противоречие. , а m, по предположению, минимальное число с таким свойством. Противоречие.
Пусть m нечетно. Тогда числа n можно представить в виде n можно представить в виде n =q =q m+m m+m ( ( ). причем |m ). причем |m |< |< . Тогда . Тогда
mp=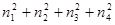 =sm+ =sm+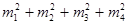 , ,
где s - некоторое целое число.
Следовательно, 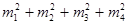 =mn , где n - неотрицательное целое число. Если n=0, то все m =mn , где n - неотрицательное целое число. Если n=0, то все m =0, n =0, n =q =q m, и тогда mp= m, и тогда mp=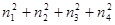 =m =m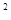 k, где k - натуральное, т. е. p=mk, m<p, а это означает, что m=1. Предположим теперь, что n k, где k - натуральное, т. е. p=mk, m<p, а это означает, что m=1. Предположим теперь, что n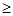 1. По теореме Гурвица получаем 1. По теореме Гурвица получаем
(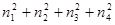 )( )(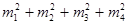 )= )=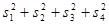 , где , где
s = =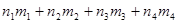 , ,
s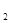 = =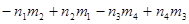 , ,
s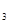 = =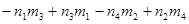 , ,
s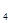 = =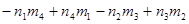 . .
По определению, m n n (mod m), т. е. s (mod m), т. е. s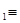 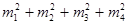  0(mod m) и, значит, 0(mod m) и, значит, 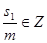 . Аналогично доказывается, что . Аналогично доказывается, что 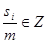 при i=2, 3, 4. Но тогда (в силу неравенств |m при i=2, 3, 4. Но тогда (в силу неравенств |m |< |<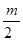 ) получаем: nm= ) получаем: nm=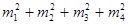 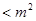 , т. е. n<m, и в итоге mp*nm= , т. е. n<m, и в итоге mp*nm=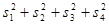 , откуда np= , откуда np=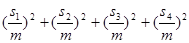 , что противоречит минимальности m. Итак, всякое простое число можно представить в виде суммы четырех квадратов целых чисел. Тогда, по теореме Гурвица, и любое составное число представимо в таком виде. Наконец, 1= , что противоречит минимальности m. Итак, всякое простое число можно представить в виде суммы четырех квадратов целых чисел. Тогда, по теореме Гурвица, и любое составное число представимо в таком виде. Наконец, 1=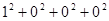 . Теорема доказана.[6] . Теорема доказана.[6]
Пример 3.
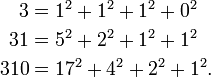
Заключение
Мы рассмотрели различные системы «чисел», которые можно построить, исходя из действительных чисел, путем добавления рядя «мнимых единиц». Доказали, что существуют тождества с большим, чем 2, числом квадратов и описали их (теорема Гурвица). Было выяснено, что
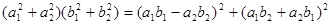
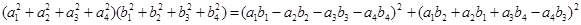 + +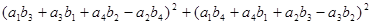
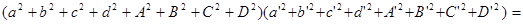
=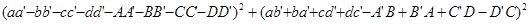 + +
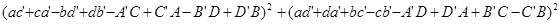 + +
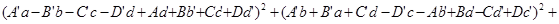
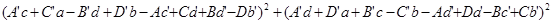
Так же было найдено приложение теоремы Гурвица.
Я добилась целей, которые перед собой поставила.
Список
используемой
литературы
1. Charles W. Curtis “Linear algebra” An Introductory Approach (Fourth Edition), Springer Verlag, 1984, xvii - 347 pp.
2. Rowe David E. “Jewish Mathematics” at Göttingen in the Era of Felix Klein. Isis, Vol. 77, No. 3, (Sep., 1986) – 432 pp
3. Калужин Л. А. “Основная теорема арифметики, Популярные лекции по математике” М.: Наука, 1969 г. - 32 стр.
4. Кантор И.Л., Солодовников А.С. “Гиперкомплексные числа” М.: Наука, 1973. - 144 с.
5. Тиморин В.А. “Квадратичная математика” - 2005
6. Тихомиров В. М. “ Великие математики прошлого и их великие теоремы” М.: МЦНМО, 2003.- 16 с.
7. Херстейн И. “Некоммутативные кольца” М.: Мир, 1972. - 192 c.
|