|
Вятский Государственный Гуманитарный Университет
Кафедра математического анализа и МПМ
Выпускная квалификационная работа
Операторы проектирования.
Выполнил студент 5курса
математического факультета
Лежнин В.В.
/подпись/
Научный руководитель:
Старший преподаватель кафедры математического анализа и МПМ
Гукасов А.К.
/подпись/
Рецензент:
Старший преподаватель кафедры математического анализа и МПМ
Подгорная М.И.
/подпись/
 Зав. кафедрой М.В. Крутихина Зав. кафедрой М.В. Крутихина
  /подпись/ << >> /подпись/ << >>
   /подпись/ << >> /подпись/ << >>
Киров
2003
Оглавление.
Введение. 2
Часть
I
.
Основные понятия и предложения.
2
Часть
II
.
Дополняемость в гильбертовых пространствах.
10
Часть
III
.
Задача о дополняемости.
13
Литература. 15
Введение.
В данной работе рассматриваются операторы проектирования, которые являются частным случаев линейных операторов, их некоторые свойства, и рассматривается вопрос: как с помощью операторов проектирования можно выяснить дополняемо множество или нет. Так же освящается тема дополняемости в гильбертовых пространствах. Попутно для рассмотрения предлагаются некоторые определения и факты, на которые опираются нужные нам утверждения. К самостоятельно выполненным заданиям относятся доказательство замкнутости ядра (стр. 6, предложение 2), формула изменения коэффициентов Фурье при сдвиге на некоторое вещественное число и решение задачи о дополняемости.
Часть
I
.
Основные понятия и предложения.
Определение.
Метрику в на векторном пространстве X будем называть инвариантной, если d(x+z,y+z)=d(x,y), для любых x,y,z из X.
Определение.
Пусть в – метрика на множестве X. Если каждая последовательность Коши сходится в X к некоторой точке, то в называется полной метрикой на X.
Определение.
Векторное пространство X называется нормированным пространством, если каждому элементу x из X сопоставлено неотрицательное вещественное число , именуемое нормой x, и выполняются следующие условия: , именуемое нормой x, и выполняются следующие условия:
1.  £ £  + + "x, yÎX. "x, yÎX.
2.  = =   "xÎX, "a - скаляра. "xÎX, "a - скаляра.
3.  > 0, если x¹0. > 0, если x¹0.
Примеры нормированных пространств.
1) l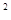 - нормированное пространство, в котором элементы – последовательности комплексных чисел x=(x
- нормированное пространство, в котором элементы – последовательности комплексных чисел x=(x , …,x , …,x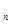 , …), удовлетворяющие условию , …), удовлетворяющие условию  <¥, <¥,
норма в таком пространстве определяется  ; ;
2) L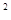 (0,1) - нормированное пространство, состоящее из функций с интегрируемым квадратом на интервале (0, 1), удовлетворяющее условию (0,1) - нормированное пространство, состоящее из функций с интегрируемым квадратом на интервале (0, 1), удовлетворяющее условию  dx < ¥, и норма определена как dx < ¥, и норма определена как  = = 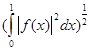 . .
3) С [0, 2p] – пространство непрерывных 2p периодических функций на отрезке [0, 2p]. Норма в нем определяется [0, 2p] – пространство непрерывных 2p периодических функций на отрезке [0, 2p]. Норма в нем определяется  = = 
Определение.
Пусть X, Y – два топологических линейных пространства. Линейным оператором, действующим из X в Y, называется отображение y = Ax, где x принадлежит X, а y принадлежит Y, удовлетворяющее условию
A(ax +bx +bx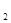 ) = aAx ) = aAx +bAx +bAx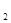 . .
Определение.
Оператор A называется непрерывным в точке x области определения, если для любой окрестности V точки y области определения, если для любой окрестности V точки y = Ax = Ax существует такая окрестность U точки x существует такая окрестность U точки x , что Ax принадлежит V, как только x принадлежит пересечению области определения и U. Оператор A называется непрерывным, если он непрерывен в каждой точке области определения. , что Ax принадлежит V, как только x принадлежит пересечению области определения и U. Оператор A называется непрерывным, если он непрерывен в каждой точке области определения.
Определение.
Линейный оператор,
действующий из Е в Е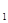 , называется ограниченным, если он определен на всем Е и каждое ограниченное множество переводит снова в ограниченное. , называется ограниченным, если он определен на всем Е и каждое ограниченное множество переводит снова в ограниченное.
Предложение 1.
Всякий непрерывный линейный оператор ограничен.
Доказательство.
Пусть М – подмножество ограниченного множества Е, а подмножество АМ множества Е не ограничено. Тогда в Е не ограничено. Тогда в Е найдется такая окрестность нуля V, что ни одно из множеств найдется такая окрестность нуля V, что ни одно из множеств 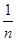 АМ не содержится в V. То тогда существует такая последовательность х АМ не содержится в V. То тогда существует такая последовательность х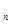 из М, что ни один из элементов из М, что ни один из элементов 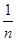 Ах Ах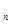 не принадлежит V, и получается, что не принадлежит V, и получается, что 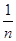 х х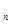 ® 0 в Е, но последовательность { ® 0 в Е, но последовательность {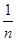 Ах Ах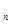 } } не сходится к 0 в Е не сходится к 0 в Е , а это противоречит непрерывности оператора А. , а это противоречит непрерывности оператора А.
В нормированных пространствах определение ограниченности линейных операторов можно сформулировать так: оператор А ограничен, если существует такая постоянная С, что для всякого f из Е
 . .
Наименьшее из чисел С, удовлетворяющее этому неравенству, называется нормой оператора А и обозначается  . .
Определение.
Пусть X - векторное пространство. Линейное отображение P:X → X называется проектором в пространстве X, если  , т.е. P(P(x)) = Px для любого элемента x из X. , т.е. P(P(x)) = Px для любого элемента x из X.
Свойства проекторов
.
Пусть P проектор в X с ядром N(P) и образом R(P).
1. R(P) = N(I-P) = {xÎX, Px = x}, где I – тождественное отображение;
2. R(P)ÇN(P) = {0} и X = R(P)+N(P);
Доказательство 1.
а) Так как (I-P)P = IP-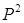 = P-P = 0, то R(P) содержится в N(I-P); = P-P = 0, то R(P) содержится в N(I-P);
б) Если x принадлежит N(I-P), то x-Px = 0, следовательно, x = Px принадлежит R(P), значит N(I-P) содержится в R(P);
Таким образом, из а) и б) следует, что R(P) = N(I-P).
Доказательство 2.
Если x принадлежит пересечению R(P) и N(P), то x=Px=0, а следовательно, R(P) и N(P) пересекаются по {0};
Для любого x из X можно представить в виде x=Px+(x-Px), где Px принадлежит R(P) и x-Px принадлежит N(P), значит X=R(P)+N(P);
Определение.
М – замкнутое подпространство топологического векторного пространства X. Если в X существует такое замкнутое подпространство N, что X=M+N и MÇN={0}, то говорят, что М дополняемо в X и что X является прямой суммой подпространств X=MÅN.
Определение.
Топологическое векторное пространство X называется F-пространством, если топология порождается некоторой полной инвариантной метрикой.
Теорема
o
замкнутом графике.
Предположим, что X и Y являются F-пространствами, отображение Т:X→Y линейно и множество G={(x, Tx): xÎX} (его график) замкнуто в X´Y. Тогда Т – непрерывно.
Предложение 2.
Пусть Ù - линейный функционал на топологическом векторном пространстве X. Допустим, что Ùx ¹0 для некоторого x из X.
Тогда если Ù непрерывен, то ядро N(Ù) замкнуто в X.
Доказательство.
Так как N(Ù) = Ù ({0}), а {0} – замкнутое множество поля скаляров (как любое одноточечное подмножество), то тогда непрерывность Ù влечет замкнутость ядра (как прообраз замкнутого множества при непрерывном отображении). ({0}), а {0} – замкнутое множество поля скаляров (как любое одноточечное подмножество), то тогда непрерывность Ù влечет замкнутость ядра (как прообраз замкнутого множества при непрерывном отображении).
Теорема 1.
а) Если Р – непрерывный проектор в топологическом векторном пространстве X, то X представляется в виде прямой суммы подпространств X=R(P)ÅN(P);
б) Обратно: если Х является F-пространством и X представляется в виде прямой суммы подпространств Х=АÅВ, то проектор Р с образом А и ядром В непрерывен.
Доказательство:
а) Так как Р и I-P непрерывны, то подпространства N(P) и R(P)=N(I-P) замкнуты (см. предложение 2), значит по второму свойству проекторов X=R(P)ÅN(P);
Чтобы доказать б) достаточно проверить, что проектор Р удовлетворяет условиям теоремы о замкнутом графике .
Пусть последовательности x →x и Px →x и Px →y. →y.
Так как Px принадлежит А, А – замкнуто, следовательно y принадлежит A, а значит y = Py. принадлежит А, А – замкнуто, следовательно y принадлежит A, а значит y = Py.
Аналогично x - Px - Px принадлежит В, В – замкнуто, следовательно x-y принадлежит B, значит Py = Px поэтому y = Px. Получили, что точка (x, y) принадлежит G (см. теорему о замкнутом графике). Отсюда вытекает, что проектор Р непрерывен. принадлежит В, В – замкнуто, следовательно x-y принадлежит B, значит Py = Px поэтому y = Px. Получили, что точка (x, y) принадлежит G (см. теорему о замкнутом графике). Отсюда вытекает, что проектор Р непрерывен.
Определение
.
Топологической группой называется группа G, снабженная такой топологией, относительно которой групповые операции в G непрерывны.
Расшифровка этого определения состоит в том, что постулируется непрерывное отображение j:G´G®G, определенного равенством: j(x,y)=xy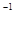 . .
Определение.
Топологическая группа G, топология которой компактна, называется компактной группой.
Определение
.
Топологическое векторное пространство X называется локально выпуклым, если в нем всякое непустое открытое множество содержит непустое выпуклое открытое подмножество.
Определение.
Пространство X называется пространством Фреше , если оно является локально выпуклым F-пространством.
Определение.
Предположим, что топологическое векторное пространство X и топологическая группа G связаны следующим образом: кждому элементу s из G сопоставлен непрерывный линейный оператор T :X®X, причем :X®X, причем
T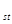 = T = T T T , где s, t принадлежат G , где s, t принадлежат G
и отображение (s, x) ® T x прямого произведения G´X в пространстве X непрерывно. В этом случае говорят, что группа G непрерывно и линейно действует в пространстве X. x прямого произведения G´X в пространстве X непрерывно. В этом случае говорят, что группа G непрерывно и линейно действует в пространстве X.
Теорема 2
.
Пусть Y – дополняемое подпространство Фреше Х, и пусть компактная группа G непрерывна и линейно действует на Х, причем Т (Y)ÌY для любого sÎG. Тогда существует непрерывный проектор Q пространства Х на подпространство Y, коммутирующий со всеми операторами Т (Y)ÌY для любого sÎG. Тогда существует непрерывный проектор Q пространства Х на подпространство Y, коммутирующий со всеми операторами Т . .
Лемма Фату.
Пусть на множестве E задана последовательность измеримых, почти всюду конечных функций f (x), которая сходится по мере к некоторой почти всюду конечной функции f . Тогда (x), которая сходится по мере к некоторой почти всюду конечной функции f . Тогда
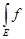 dm £ dm £   dm dm
Пример недополняемого подпространства.
Рассмотрим подпространство Y=H пространства Х=L пространства Х=L , где L , где L - пространство всех суммируемых функций на комплексной плоскости, а H - пространство всех суммируемых функций на комплексной плоскости, а H состоит из всех функций L состоит из всех функций L , для которых , для которых 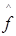 (n)=0, при всех n<0. (n)=0, при всех n<0. 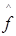 (n) обозначает n-ый коэффициент Фурье функции f и вычисляется: (n) обозначает n-ый коэффициент Фурье функции f и вычисляется:
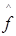 (n)= (n)=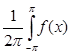 e e dx, (n=0, dx, (n=0, 1, 1,  2, …). (1) 2, …). (1)
(для простоты обозначается: f(x)=f(e 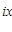 )). )).
В качестве группы G возьмем мультипликативную группу всех комплексных чисел, по модулю равных 1, и сопоставим каждому элементу
e 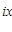 ÎG оператор сдвига t ÎG оператор сдвига t , полагая, что , полагая, что
(t f)(x) = f(x+s), где s – некоторое вещественное число. (2) f)(x) = f(x+s), где s – некоторое вещественное число. (2)
Теперь посмотрим, как изменяются коэффициенты Фурье при таком сдвиге: (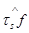 )(n) = )(n) =  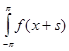 e e  dx. dx.
Произведем замену: x+s = t Þ x = t-s. Тогда
( )(n)= )(n)=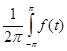 e e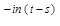 d(t-s) = d(t-s) =
= 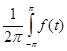 e e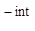 e e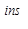 dt=e dt=e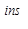 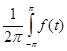 e e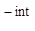 dt=e dt=e 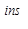 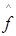 (n), (n),
то есть (t f) f) (n)= e (n)= e 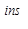 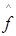 (n). (3). (n). (3).
Так как e 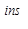 ÎG, то t ÎG, то t (H (H ) = H ) = H для любого вещественного s. для любого вещественного s.
Если бы подпространство H было дополняемо в L было дополняемо в L , то из Т2. следовало бы существование такого непрерывного проектора Q пространства L , то из Т2. следовало бы существование такого непрерывного проектора Q пространства L на H на H , что t , что t Q = Qt Q = Qt для любого вещественного s. (4). для любого вещественного s. (4).
Найдем вид проектора. Положим e (x)=e (x)=e  . Тогда t . Тогда t e e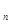 =e =e e e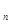 , а так как оператор Q линеен, то , а так как оператор Q линеен, то
Qt e e = e = e Qe Qe . (5). . (5).
Из (4) и (5) следует, что
(Qe )(x-s) = e )(x-s) = e  (Qe (Qe )(x). (6). )(x). (6).
Пусть С = (Qe = (Qe )(0). При Q = 0 соотношение (6) имеет вид )(0). При Q = 0 соотношение (6) имеет вид
Qe = C = C e e . (7). . (7).
Воспользуемся тем, что образом оператора Q служит подпространство Н . Так как Qe . Так как Qe  принадлежит H принадлежит H для любого n, то из (7) следует, что для любого n, то из (7) следует, что
С = 0 для любого n<0. Так как Qf = f для любого f из H = 0 для любого n<0. Так как Qf = f для любого f из H , то С , то С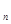 = 1 при любом n³0. = 1 при любом n³0.
Таким образом, проектор Q должен являться «естественным», то есть его действие сводится к замене нулями всех коэффициентов Фурье с отрицательными номерами:
Q( e e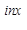 )= )= e e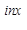 . (8). . (8).
Рассмотрим функцию f (x) = (x) =  e e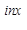 , (0<r<1), (9). , (0<r<1), (9).
которая представляет собой ядро Пуассона:  , в частности f , в частности f >0. Поэтому >0. Поэтому
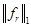 = =  dx = dx =  dx = 1 для любого r. (10) Но (Qf dx = 1 для любого r. (10) Но (Qf )(x) = )(x) =  e e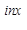 = =  (11). (11).
Так как 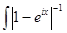 dx = ¥, то из леммы Фату следует, что dx = ¥, то из леммы Фату следует, что  ® ¥, при ® ¥, при
r ® 1. В силу (10) это противоречит непрерывности оператора Q.
Таким образом, доказано, что H недополняемо в L недополняемо в L . .
Часть
II
.
Дополняемость в гильбертовых пространствах.
Гильбертово пространство.
Комплексное векторное пространство Н называется пространством с внутренним произведением (унитарное пространство), если каждой упорядоченной паре векторов x,y из Н сопоставлено комплексное число (x,y), называемое скалярным и:
а) (y,x)= , "x, yÎH; , "x, yÎH;
b) (x+y,z)=(x+z)+(y+z), "x, y, zÎH;
c) (ax,y)=a(x,y), "x, yÎH, "aÎC;
d) (x,x)³0, "xÎH;
e) (x,x)=0 Û x=0, "xÎH;
Если (x,y) = 0, то говорят, что x ортогонален y (обозначение x^y).
Если Е подмножество Н, F подмножество H, то Е^F обозначает, что (x,y) = 0 для любых x из E и любых y из F.
Через Е обозначаются все y из H, ортогональные каждому из векторов x из E. обозначаются все y из H, ортогональные каждому из векторов x из E.
Нормой в пространстве Н называется число  . .
Если полученное нормированное пространство является полным, то оно называется гильбертовым пространством.
Примеры гильбертовых пространств.
1) l - комплексное гильбертово пространство, в котором скалярное произведение определяется формулой (x, y) =
- комплексное гильбертово пространство, в котором скалярное произведение определяется формулой (x, y) =  ; ;
2) L (0,1) - гильбертово пространство, в котором скалярное произведение определено формулой (0,1) - гильбертово пространство, в котором скалярное произведение определено формулой
(f, g) =  dx. dx.
Теорема3:
М – замкнутое подпространство гильбертова пространства Н, следовательно H можно представить в виде прямой суммы M и М (Н=МÅМ (Н=МÅМ , М , М - ортогональное дополнение к М). - ортогональное дополнение к М).
Доказательство:
Если Е подмножество Н, то из линейности скалярного произведения (x,y) по x следует, что Е является подпространством в Н. Допустим, что элементы g является подпространством в Н. Допустим, что элементы g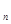 принадлежат Е принадлежат Е и сходятся к g. Тогда для любого f из E и сходятся к g. Тогда для любого f из E
(g, f) =  = 0, и потому g тоже входит в Е = 0, и потому g тоже входит в Е , значит Е , значит Е - замкнутое подпространство. - замкнутое подпространство.
(1) Если х принадлежит М и х принадлежит М , то (х, х) = 0, а это будет тогда и только тогда, когда х = 0, следовательно МÇМ , то (х, х) = 0, а это будет тогда и только тогда, когда х = 0, следовательно МÇМ ={0}. ={0}.
(2) Пусть х принадлежит Н.
Рассмотрим множество х-М = {х-х : х : х ÎМ}, причем х ÎМ}, причем х такой, что он минимизирует величину такой, что он минимизирует величину  . Пусть х . Пусть х = х-х = х-х , следовательно, , следовательно,  £ £ для любых y из М, значит, х для любых y из М, значит, х принадлежит М принадлежит М , поэтому для любого х из Н х можно представить в виде х = х , поэтому для любого х из Н х можно представить в виде х = х +х +х , где х , где х из М и х из М и х из М из М . .
Из (1) и (2) следует, что Н представимо в виде прямой суммы М и М Н=МÅМ Н=МÅМ , следовательно любое подмножество в гильбертовом пространстве дополняемо. , следовательно любое подмножество в гильбертовом пространстве дополняемо.
Примеры дополняемых подпространств в гильбертовом пространстве.
1) в l рассмотрим элементы x = (x
рассмотрим элементы x = (x , …,x , …,x , …), у которых x , …), у которых x = 0 при четных n и x = 0 при четных n и x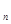 произвольные при n нечетных. Эти элементы образуют в l произвольные при n нечетных. Эти элементы образуют в l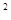 замкнутое подпространство. Назовем его X.
замкнутое подпространство. Назовем его X.
Рассмотрим также элементы y = (y , …, y , …, y , …), у которых y , …), у которых y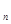 произвольные при четных n, и y произвольные при четных n, и y = 0 при нечетных n. Эти элементы образуют замкнутое подпространство в l = 0 при нечетных n. Эти элементы образуют замкнутое подпространство в l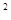 ,
и при этом это подпространство является ортогональным дополнением к X, так как их скалярное произведение равно 0. Следовательно, по Т3. X дополняемо в H с помощью X
,
и при этом это подпространство является ортогональным дополнением к X, так как их скалярное произведение равно 0. Следовательно, по Т3. X дополняемо в H с помощью X . .
2) L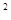 (0,1). (0,1).
Пусть X – подпространство L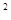 (0,1), состоящее из тех функций L (0,1), состоящее из тех функций L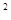 (0,1), которые обращаются в 0 на интервале (0, а]. (0,1), которые обращаются в 0 на интервале (0, а].
Пусть Y – подпространство L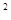 (0,1), состоящее из тех функций L (0,1), состоящее из тех функций L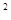 (0,1), которые в ноль не обращаются на интервале [a, 1). (0,1), которые в ноль не обращаются на интервале [a, 1).
Тогда Y является ортогональным дополнением X, так как их скалярное произведение равно 0, а значит X дополняемо в L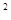 (0,1) с помощью Y. (0,1) с помощью Y.
Часть
III
.
Задача о дополняемости.
Пусть С [0, 2p] - множество непрерывных 2p периодических функций на отрезке [0, 2p]. [0, 2p] - множество непрерывных 2p периодических функций на отрезке [0, 2p].
Пусть Е – множество четных чисел и пусть
С = {f(x)Î С = {f(x)Î С : :  (n) = 0 "nÏE}. (n) = 0 "nÏE}.
Требуется доказать, что С дополняемо в С дополняемо в С [0, 2p]. [0, 2p].
Доказательство:
Чтобы доказать требуемое, необходимо найти такой непрерывный проектор, который бы отображал множество С [0, 2p] на С [0, 2p] на С (Т1.), таким образом, чтобы коэффициенты Фурье функций, стоящие на нечетных номерах, отображались бы в 0, а на четных оставались бы без изменения. (Т1.), таким образом, чтобы коэффициенты Фурье функций, стоящие на нечетных номерах, отображались бы в 0, а на четных оставались бы без изменения.
Рассмотрим оператор P =  (t (t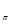 +I), где t +I), где t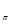 - оператор сдвига на p, а I - тождественное отображение. - оператор сдвига на p, а I - тождественное отображение.
t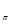 ограничен, так как мы имеем дело с 2p периодическими функциями, так как ограничен, так как мы имеем дело с 2p периодическими функциями, так как
 = =  = 1 = 1 , то есть С = 1. , то есть С = 1.
А раз он ограничен, то следовательно и непрерывен (предложение 1).
I - тоже непрерывен.
Теперь посмотрим, как изменятся коэффициенты Фурье функций при таком отображении.
1) n = 2k-1, где к – целое.
 (( (( )(2k-1)+( )(2k-1)+( )(2k-1)) = )(2k-1)) =
=  (e (e   (2k-1)+ (2k-1)+  (2k-1)) = (2k-1)) =   (2k-1)( e (2k-1)( e  +1). (*) +1). (*)
Так как e  =cos j+isin j, значит e =cos j+isin j, значит e  = cos ((2k-1)p)+isin((2k-1)p). = cos ((2k-1)p)+isin((2k-1)p).
При любом k – целом выражение cos ((2k-1)p)+isin((2k-1)p) = -1, а, следовательно, и выражение (*) принимает значение 0. Мы показали, что коэффициенты Фурье функций, стоящие на нечетных номерах при таком отображении обращаются в 0.
2) n=2k, где k – целое.
 (( (( )(2k)+( )(2k)+(  )(2k)) = )(2k)) =  (e (e 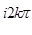  (2k)+ (2k)+  (2k)) = (2k)) =
=   (2k)( e (2k)( e 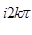 +1). (**) +1). (**)
При любом k – целом выражение cos (2kp)+isin(2kp) = 1, а следовательно и выражение (**) не изменяет своего значения, то есть равно  (2k). Мы показали, что коэффициенты Фурье функций, стоящие на четных номерах при таком отображении не изменяются, то есть оператор Р действительно является проектором. (2k). Мы показали, что коэффициенты Фурье функций, стоящие на четных номерах при таком отображении не изменяются, то есть оператор Р действительно является проектором.
Таким образом, нашелся такой непрерывный проектор P: С [0, 2p]® С [0, 2p]® С , следовательно С , следовательно С дополняемо в С дополняемо в С [0, 2p]. [0, 2p].
Литература.
1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М., Наука. 1989.
2. Рудин Уолтер. Функциональный анализ. М., Наука. 1975.
3. Вулих Б.З. Краткий курс в теорию функций вещественной переменной. М., Наука. 1973.
|