| Содержание
Задание 1
Задание 2
Список литературы
Вариант 6
Задание 1
Имеются данные, характеризующие выручку (у, млн. руб.) предприятия «АВС» в зависимости от капиталовложений (х, млн. руб.) за последние 10 лет (табл. 1).
Таблица 1
| Время, t
|
1998
|
1999
|
2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
| Выручка, у
|
3,0
|
2,9
|
3,0
|
3,1
|
3,2
|
2,8
|
2,9
|
3,4
|
3,5
|
3,6
|
| Объем капитало-
вложений, х
|
1,1
|
1,1
|
1,2
|
1,4
|
1,4
|
1,4
|
1,3
|
1,6
|
1,3
|
1,4
|
1. Построить поле корреляции.
2. Найти параметры уравнения линейной регрессии 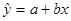 ; дать экономическую интерпретацию параметров а и b. ; дать экономическую интерпретацию параметров а и b.
3. Составить уравнения нелинейных регрессий:
· гиперболической  ; ;
· степной 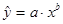 ; ;
· показательной 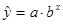
4. Для каждой из моделей:
- найти коэффициент парной корреляции (для нелинейных регрессий – индекс корреляции);
- найти коэффициент детерминации;
- проверить значимость уравнения регрессии в целом с помощью F – критерия Фишера;
- найти среднюю относительную ошибку аппроксимации.
5. Составить сводную таблицу вычислений; выбрать лучшую модель; дать интерпретацию рассчитанных характеристик.
6. По лучшей модели составить прогноз на следующие два года показателя у (выручка), если х (объем капиталовложений) увеличивается на 10% по сравнению с последним годом.
7. Построить графики уравнений регрессии; отметить точки прогноза.
РЕШЕНИЕ:
1.
ПОСТРОИМ ПОЛЕ КОРРЕЛЯЦИИ
Поле корреляции – точечный график, осями X и Y которого сопоставлены изучаемые признаки (рис. 1).

Рис. 1
Точки на графике поля корреляции находятся довольно хаотично, что говорит о слабой зависимости объема капиталовложений Х и выручки Y.
2.
НАЙДЕМ ПАРАМЕТРЫ ЛИНЕЙНОЙ РЕГРЕССИИ 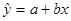
Расчет неизвестных параметров выполним методом наименьших квадратов (МНК), построив систему нормальных уравнений и решая ее, относительно неизвестных параметров а и b.
Система нормальных уравнений имеет вид:
 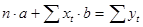

Необходимые расчеты представлены в таблице 2.
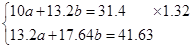 


Построена линейная модель зависимости выручки предприятия «АВС» от объема капиталовложений:

В линейном регрессии коэффициент регрессии показывает направление связи между переменной Y и фактором X. А также, указывает насколько в среднем изменяется значение результативного признака Y, если фактор увеличить на единицу измерения.
b = 0,843, т.е. при увеличении объема капиталовложений (Х) на 1 млн. руб. выручка предприятия (Y) в среднем увеличится на 0,843 млн. руб.
Таблица 2
Вспомогательные вычисления для нахождения параметров линейной модели
| t
|
Y
|
X
|
X2
|
X*Y
|
| 1998
|
3,0
|
1,1
|
1,21
|
3,3
|
| 1999
|
2,9
|
1,1
|
1,21
|
3,19
|
| 2000
|
3,0
|
1,2
|
1,44
|
3,6
|
| 2001
|
3,1
|
1,4
|
1,96
|
4,34
|
| 2002
|
3,2
|
1,4
|
1,96
|
4,48
|
| 2003
|
2,8
|
1,4
|
1,96
|
3,92
|
| 2004
|
2,9
|
1,3
|
1,69
|
3,77
|
| 2005
|
3,4
|
1,6
|
2,56
|
5,44
|
| 2006
|
3,5
|
1,3
|
1,69
|
4,55
|
| 2007
|
3,6
|
1,4
|
1,96
|
5,04
|
| Σ
|
31,4
|
13,2
|
17,64
|
41,63
|
3.
РАССЧИТАЕМ:
- коэффициент парной корреляции.
Коэффициент парной корреляции показывает направление и тесноту линейной связи.

 

Т. е. связь между объемом капиталовложений и выручкой предприятия прямая и слабая.
Таблица 3
Вспомогательная таблица для расчета коэффициента парной корреляции, средней относительной ошибки аппроксимации
| t
|
Y
|
X
|

|

|

|
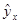
|
A
|
| 1998
|
3,0
|
1,1
|
0,048
|
0,020
|
0,031
|
2,955
|
0,015
|
| 1999
|
2,9
|
1,1
|
0,048
|
0,058
|
0,053
|
2,955
|
0,019
|
| 2000
|
3,0
|
1,2
|
0,014
|
0,020
|
0,017
|
3,039
|
0,013
|
| 2001
|
3,1
|
1,4
|
0,006
|
0,002
|
-0,003
|
3,207
|
0,035
|
| 2002
|
3,2
|
1,4
|
0,006
|
0,004
|
0,005
|
3,207
|
0,002
|
| 2003
|
2,8
|
1,4
|
0,006
|
0,116
|
-0,027
|
3,207
|
0,146
|
| 2004
|
2,9
|
1,3
|
0,000
|
0,058
|
0,005
|
3,123
|
0,077
|
| 2005
|
3,4
|
1,6
|
0,078
|
0,068
|
0,073
|
3,376
|
0,007
|
| 2006
|
3,5
|
1,3
|
0,000
|
0,130
|
-0,007
|
3,123
|
0,108
|
| 2007
|
3,6
|
1,4
|
0,006
|
0,212
|
0,037
|
3,207
|
0,109
|
| Σ
|
31,4
|
13,2
|
0,216
|
0,684
|
0,182
|
|
0,530
|
коэффициент детерминации
Коэффициент детерминации показывает долю вариации результативного признака Y под влиянием фактора Х, включенного в модель.
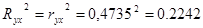
22,42% изменения выручки предприятия обусловлено изменением объема капиталовложений, на 77,58% влиянием прочих факторов, не учтенных в модели.

Рис. 2
F – критерий Фишера
Для проверки значимости уравнения регрессии в целом найдем расчетное значение критерия Фишера:
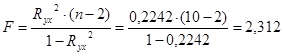
Расчетное значение статистики Фишера сравниваем с табличным
F(α; d.f.1
; d.f.2
), где
α – уровень значимости (для большей надежности примем его равным 0,05);
Число степеней свободы d.f.1
= k = 1, где k – число факторов в модели;
Число степеней свободы d.f.2
= n – k – 1 = 10 – 1 – 1 = 8
F (0.05; 1; 8) = 5,318.
В силу того, что F(расч.) = 2,312 < F(табл.)= 5,318, то уравнение в целом можно считать статистически незначимым.
Среднюю относительную ошибку аппроксимации:

Фактические значения выручки отличаются от расчетных, полученных по модели на 5,3%. Ошибка небольшая, модель считается точной
4.
НАЙДЕМ ПАРАМЕТРЫ ГИПЕРБОЛИЧЕСКОЙ МОДЕЛИ РЕГРЕССИИ 
Расчет неизвестных параметров выполним методом наименьших квадратов (МНК).
Система нормальных уравнений имеет вид:
 

Необходимые расчеты представлены в таблице 4.
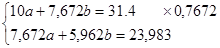 
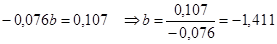

Таблица 4
Вспомогательная таблица для расчетов показателей по гиперболической модели
| t
|
Y
|
X
|
1/Х
|
1/Х^2
|
Y/X
|

|

|
A
|
| 1998
|
3,0
|
1,1
|
0,909
|
0,826
|
2,727
|
2,940
|
0,004
|
0,020
|
| 1999
|
2,9
|
1,1
|
0,909
|
0,826
|
2,636
|
2,940
|
0,002
|
0,014
|
| 2000
|
3,0
|
1,2
|
0,833
|
0,694
|
2,500
|
3,047
|
0,002
|
0,016
|
| 2001
|
3,1
|
1,4
|
0,714
|
0,510
|
2,214
|
3,215
|
0,013
|
0,037
|
| 2002
|
3,2
|
1,4
|
0,714
|
0,510
|
2,286
|
3,215
|
0,000
|
0,005
|
| 2003
|
2,8
|
1,4
|
0,714
|
0,510
|
2,000
|
3,215
|
0,172
|
0,148
|
| 2004
|
2,9
|
1,3
|
0,769
|
0,592
|
2,231
|
3,137
|
0,056
|
0,082
|
| 2005
|
3,4
|
1,6
|
0,625
|
0,391
|
2,125
|
3,341
|
0,004
|
0,017
|
| 2006
|
3,5
|
1,3
|
0,769
|
0,592
|
2,692
|
3,137
|
0,132
|
0,104
|
| 2007
|
3,6
|
1,4
|
0,714
|
0,510
|
2,571
|
3,215
|
0,148
|
0,107
|
| Σ
|
31,4
|
13,2
|
7,672
|
5,962
|
23,983
|
|
0,533
|
0,549
|
Построена гиперболическая модель зависимости выручки предприятия «АВС» от объема капиталовложений:

5.
РАССЧИТАЕМ:
- индекс корреляции:

Связь между объемом капиталовложений и выручкой предприятия в гиперболической модели слабая
- коэффициент детерминации
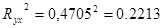
22,13% изменения выручки предприятия в гиперболической модели происходит под влиянием изменением объема капиталовложений и на 77,87% под влиянием факторов, не включенных в модель.
- F – критерий Фишера
Проверим значимость уравнения
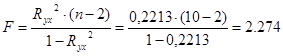
F(расч.) = 2,274< F(табл.)= 5,318, т.е. уравнение в целом можно считать статистически незначимым.
Среднюю относительную ошибку аппроксимации:
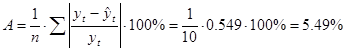
Ошибка меньше 7%, модель можно считать точной.

Рис. 3
6.
НАЙДЕМ ПАРАМЕТРЫ СТЕПЕННОЙ МОДЕЛИ РЕГРЕССИИ

Произведем линеаризацию переменных путем логарифмирования обеих частей уравнения.

Сделаем замену переменной Y = lg y, A = lg a, X = lg x. Тогда Y = A + b ∙ X – линейная модель парной регрессии. Можно применить МНК.
 
Необходимые расчеты представлены в таблице 5.
 

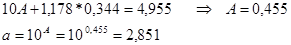
Построена степенная модель зависимости выручки предприятия «АВС» от объема капиталовложений: 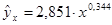
Таблица 5
Вспомогательная таблица для расчетов показателей по степенной модель
| t
|
y
|
x
|
Y = lg y
|
X = lg x
|
X2
=
=lg x2
|
X*Y =
lg x*lg y
|
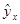
|

|
A
|
| 1998
|
3,0
|
1,1
|
0,477
|
0,041
|
0,002
|
0,020
|
2,946
|
0,003
|
0,018
|
| 1999
|
2,9
|
1,1
|
0,462
|
0,041
|
0,002
|
0,019
|
2,946
|
0,002
|
0,016
|
| 2000
|
3,0
|
1,2
|
0,477
|
0,079
|
0,006
|
0,038
|
3,035
|
0,001
|
0,012
|
| 2001
|
3,1
|
1,4
|
0,491
|
0,146
|
0,021
|
0,072
|
3,200
|
0,010
|
0,032
|
| 2002
|
3,2
|
1,4
|
0,505
|
0,146
|
0,021
|
0,074
|
3,200
|
0,000
|
0,000
|
| 2003
|
2,8
|
1,4
|
0,447
|
0,146
|
0,021
|
0,065
|
3,200
|
0,160
|
0,143
|
| 2004
|
2,9
|
1,3
|
0,462
|
0,114
|
0,013
|
0,053
|
3,120
|
0,048
|
0,076
|
| 2005
|
3,4
|
1,6
|
0,531
|
0,204
|
0,042
|
0,108
|
3,350
|
0,002
|
0,015
|
| 2006
|
3,5
|
1,3
|
0,544
|
0,114
|
0,013
|
0,062
|
3,120
|
0,145
|
0,109
|
| 2007
|
3,6
|
1,4
|
0,556
|
0,146
|
0,021
|
0,081
|
3,200
|
0,160
|
0,111
|
| Σ
|
31,4
|
13,2
|
4,955
|
1,178
|
0,163
|
0,592
|
|
0,532
|
0,531
|
7.
РАССЧИТАЕМ:
индекс корреляции:

Связь между объемом капиталовложений и выручкой предприятия в степенной модели слабая.
коэффициент детерминации

Степенная модель всего на 13,44% детерминирует зависимость выручки предприятия от объема капиталовложений. 86,56% детерминации происходит под влиянием факторов не учтенных в модели.
F – критерий Фишера
Проверим значимость уравнения
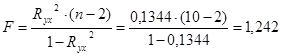
F(расч.) = 1,242 < F(табл.)= 5,318, т.е. уравнение степенной модели в целом можно считать статистически незначимым.
Среднюю относительную ошибку аппроксимации:

Ошибка меньше 7%, степенную модель можно считать точной.

Рис. 4
8.
НАЙДЕМ ПАРАМЕТРЫ ПОКАЗАТЕЛЬНОЙ МОДЕЛИ РЕГРЕССИИ 
Произведем линеаризацию переменных путем логарифмирования обеих частей уравнения.
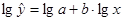
Сделаем замену переменной Y = lg y, A = lg a, В = lg b. Тогда Y = A + B ∙ x – линейная модель парной регрессии. Можно применить МНК.
 
Необходимые расчеты представлены в таблице 6.
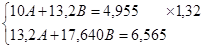 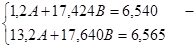
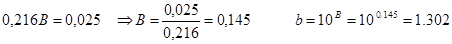

Таблица 6
Вспомогательная таблица для расчетов показателей по показательной модели
| t
|
y
|
x
|
Y = lg y
|
x2
|
x*Y =
x*lg y
|
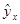
|

|
A
|
| 1998
|
3,0
|
1,1
|
0,477
|
1,21
|
0,525
|
2,953
|
0,002
|
0,016
|
| 1999
|
2,9
|
1,1
|
0,462
|
1,21
|
0,509
|
2,953
|
0,003
|
0,018
|
| 2000
|
3,0
|
1,2
|
0,477
|
1,44
|
0,573
|
3,032
|
0,001
|
0,011
|
| 2001
|
3,1
|
1,4
|
0,491
|
1,96
|
0,688
|
3,196
|
0,009
|
0,031
|
| 2002
|
3,2
|
1,4
|
0,505
|
1,96
|
0,707
|
3,196
|
0,000
|
0,001
|
| 2003
|
2,8
|
1,4
|
0,447
|
1,96
|
0,626
|
3,196
|
0,157
|
0,141
|
| 2004
|
2,9
|
1,3
|
0,462
|
1,69
|
0,601
|
3,113
|
0,045
|
0,073
|
| 2005
|
3,4
|
1,6
|
0,531
|
2,56
|
0,850
|
3,369
|
0,001
|
0,009
|
| 2006
|
3,5
|
1,3
|
0,544
|
1,69
|
0,707
|
3,113
|
0,150
|
0,111
|
| 2007
|
3,6
|
1,4
|
0,556
|
1,96
|
0,779
|
3,196
|
0,163
|
0,112
|
| Σ
|
31,4
|
13,2
|
4,955
|
17,640
|
6,565
|
|
0,531
|
0,524
|
Построена показательная модель зависимости выручки предприятия «АВС» от объема капиталовложений: 
9.
РАССЧИТАЕМ:
индекс корреляции:

Связь между объемом капиталовложений и выручкой предприятия в степенной модели очень слабая.
коэффициент детерминации

В показательной модели изменение выручки на 22,30% обусловлено изменением объема капиталовложений, на 77,70% - влиянием факторов, не включенных в модель.
F – критерий Фишера
Проверим значимость уравнения
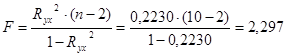
F(расч.) = 2,297 < F(табл.) = 5,318, т.е. показательное уравнение в целом можно считать статистически незначимым.
Среднюю относительную ошибку аппроксимации:

Ошибка меньше 7%, показательную модель можно считать точной.
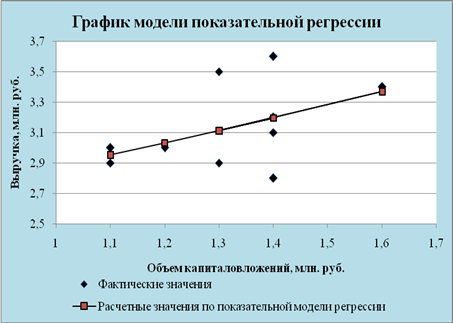
Рис. 5
10.
СОСТАВИМ СВОДНУЮ ТАБЛИЦУ ВЫЧИСЛЕНИЙ (таблица 7)
Таблица 7
| Пар-
аметры
|
Модель
|
| линейная
|
гиперболическая
|
степенная
|
показательная
|
| 
|
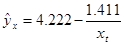
|

|

|
| Ryx
|
0,4735
|
0,4705
|
0,3666
|
0,4723
|
| Ryx
2
|
0,2242
|
0,2213
|
0,1344
|
0,2230
|
| Fрасч
|
2,31
|
2,27
|
1,24
|
0,78
|
| A, %
|
5,30
|
5,49
|
5,31
|
5,24
|
Все модели имеют примерно одинаковые характеристики. Но большее значение индекса корреляции, коэффициента детерминации, F – критерия Фишера и меньшее значение средней относительной ошибки аппроксимации имеет линейная модель. Т.е. она лучше и точнее из всех построенных моделей описывает зависимость выручки от объема капиталовложений.
Ее можно взять в качестве лучшей для построения прогноза.
11.
СДЕЛАЕМ ПРОГНОЗ НА СЛЕДУЮЩИЕ ДВА ГОДА показателя у
(выручка), если х (объем капиталовложений) увеличивается на 10 % по сравнению с последним годом.
Лучшей является линейная модель вида 
Сначала найдем прогнозные значения показателя х (объем капиталовложений). В 2007 году объем капиталовложений составил 1,4 млн. руб. Следовательно, в 2008 году он составит – 1,4 ∙ 1,1 = 1,54 млн. руб., а в 2009 году - 1,54 ∙ 1,1 = 1,69 млн. руб.
Подставим прогнозные значения х в уравнение регрессии 
Это будут точечные прогнозы результата у (выручка предприятия).
В 2008 году выручка предприятия составит: 2,028+0,843*1,54 = 3,33 (млн. руб.)
В 2009 году: 2,028+0,843*1,69 = 3,46 (млн. руб.)

Рис. 6
Задание 2
Имеются данные, характеризующие выручку (у, млн. руб.) предприятия «АВС» в зависимости от капиталовложений (х1
, млн. руб.) и основных производственных фондов (х2
, млн. руб.) за последние 10 лет (табл. 8)
Таблица 8
| Время, t
|
1998
|
1999
|
2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
| Выручка, у
|
3,0
|
2,9
|
3,0
|
3,1
|
3,2
|
2,8
|
2,9
|
3,4
|
3,5
|
3,6
|
| Объем капитало-
вложений, х1
|
1,1
|
1,1
|
1,2
|
1,4
|
1,4
|
1,4
|
1,3
|
1,6
|
1,3
|
1,4
|
| Основные
производственные фонды, х2
|
0,4
|
0,4
|
0,7
|
0,9
|
0,9
|
0,8
|
0,8
|
1,1
|
0,4
|
0,5
|
1.
Построить матрицу коэффициентов парной корреляции. Сделать соответствующие выводы о тесноте связи результата у и факторов х1
и х2
. Установить, проявляется ли в модели мультиколлинеарность.
2.
Построить линейную модель множественной регрессии 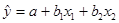 ; дать экономическую интерпретацию параметров b1
и b2
. ; дать экономическую интерпретацию параметров b1
и b2
.
3.
Построить степенную модель множественной регрессии  ; дать экономическую интерпретацию параметров β1
и β2
. ; дать экономическую интерпретацию параметров β1
и β2
.
4.
Для каждой из моделей:
- найти коэффициент множественной корреляции;
- найти коэффициент детерминации;
- проверить значимость уравнения регрессии в целом с помощью F – критерия Фишера;
- найти среднюю относительную ошибку аппроксимации.
5.
Составить сводную таблицу вычислений; выбрать лучшую модель.
6.
Пояснить экономический смысл всех рассчитанных характеристик.
7.
Найти частные коэффициенты эластичности и β – коэффициенты.
8.
По линейной модели регрессии сделать прогноз на следующие два года показателя у (выручка), в зависимости от х1
(объема капиталовложений) и х2
(основных производственных фондов).
РЕШЕНИЕ:
1.
ПОСТРОИМ МАТРИЦУ КОЭФФИЦИЕНТОВ ПАРНОЙ КОРРЕЛЯЦИИ.
Для этого рассчитаем коэффициенты парной корреляции по формуле:

Необходимые расчеты представлены в таблице 9.
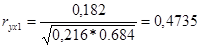 - -
связь между выручкой предприятия Y и объемом капиталовложений Х1
слабая и прямая;
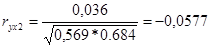 - -
связи между выручкой предприятия Y и основными производственными фондами Х2
практически нет;
 - -
связь между объемом капиталовложений Х1
и основными производственными фондами Х2
тесная и прямая;
Таблица 9
Вспомогательная таблица для расчета коэффициентов парных корреляций
| t
|
Y
|
X1
|
X2
|
(y-yср)2
|
(х1-х1ср)2
|
(x2-x2ср)2
|
(y-yср)*
(x1-x1ср)
|
(y-yср)*
(x2-x2ср)
|
(х1-х1ср)*
(x2-x2ср)
|
| 1998
|
3,0
|
1,1
|
0,4
|
0,0196
|
0,0484
|
0,0841
|
0,0308
|
0,0406
|
0,0638
|
| 1999
|
2,9
|
1,1
|
0,4
|
0,0576
|
0,0484
|
0,0841
|
0,0528
|
0,0696
|
0,0638
|
| 2000
|
3,0
|
1,2
|
0,7
|
0,0196
|
0,0144
|
1E-04
|
0,0168
|
-0,0014
|
-0,0012
|
| 2001
|
3,1
|
1,4
|
0,9
|
0,0016
|
0,0064
|
0,0441
|
-0,0032
|
-0,0084
|
0,0168
|
| 2002
|
3,2
|
1,4
|
0,9
|
0,0036
|
0,0064
|
0,0441
|
0,0048
|
0,0126
|
0,0168
|
| 2003
|
2,8
|
1,4
|
0,8
|
0,1156
|
0,0064
|
0,0121
|
-0,0272
|
-0,0374
|
0,0088
|
| 2004
|
2,9
|
1,3
|
0,8
|
0,0576
|
0,0004
|
0,0121
|
0,0048
|
-0,0264
|
-0,0022
|
| 2005
|
3,4
|
1,6
|
1,1
|
0,0676
|
0,0784
|
0,1681
|
0,0728
|
0,1066
|
0,1148
|
| 2006
|
3,5
|
1,3
|
0,4
|
0,1296
|
0,0004
|
0,0841
|
-0,0072
|
-0,1044
|
0,0058
|
| 2007
|
3,6
|
1,4
|
0,5
|
0,2116
|
0,0064
|
0,0361
|
0,0368
|
-0,0874
|
-0,0152
|
| Σ
|
31,4
|
13,2
|
6,9
|
0,684
|
0,216
|
0,569
|
0,182
|
-0,036
|
0,272
|
| Средн.
|
3,14
|
1,32
|
0,69
|
|
|
|
|
|
|
Также матрицу коэффициентов парных корреляций можно найти в среде Excel с помощью надстройки АНАЛИЗ ДАННЫХ, инструмента КОРРЕЛЯЦИЯ.
Матрица коэффициентов парной корреляции имеет вид:
| |
Y
|
X1
|
X2
|
| Y
|
1
|
|
|
| X1
|
0,4735
|
1
|
|
| X2
|
-0,0577
|
0,7759
|
1
|
Матрица парных коэффициентов корреляции показывает, что результативный признак у (выручка) имеет слабую связь с объемом капиталовложений х1
, а с Размером ОПФ связи практически нет. Связь между факторами в модели оценивается как тесная, что говорит о их линейной зависимости, мультиколлинеарности.
2.
ПОСТРОИТЬ ЛИНЕЙНУЮ МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ 
Параметры модели найдем с помощью МНК. Для этого составим систему нормальных уравнений.
 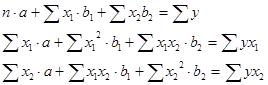
Расчеты представлены в таблице 10.
 
Решим систему уравнений, используя метод Крамера:
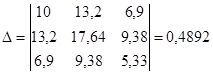 
 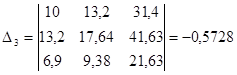
 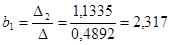 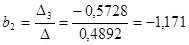
Таблица 10
Вспомогательные вычисления для нахождения параметров линейной модели множественной регрессии
| y
|
x1
|
x2
|
x1
2
|
x1*x2
|
x2
2
|
y*x1
|
y*x2
|
| 3,0
|
1,1
|
0,4
|
1,21
|
0,44
|
0,16
|
3,3
|
1,2
|
| 2,9
|
1,1
|
0,4
|
1,21
|
0,44
|
0,16
|
3,19
|
1,16
|
| 3,0
|
1,2
|
0,7
|
1,44
|
0,84
|
0,49
|
3,6
|
2,1
|
| 3,1
|
1,4
|
0,9
|
1,96
|
1,26
|
0,81
|
4,34
|
2,79
|
| 3,2
|
1,4
|
0,9
|
1,96
|
1,26
|
0,81
|
4,48
|
2,88
|
| 2,8
|
1,4
|
0,8
|
1,96
|
1,12
|
0,64
|
3,92
|
2,24
|
| 2,9
|
1,3
|
0,8
|
1,69
|
1,04
|
0,64
|
3,77
|
2,32
|
| 3,4
|
1,6
|
1,1
|
2,56
|
1,76
|
1,21
|
5,44
|
3,74
|
| 3,5
|
1,3
|
0,4
|
1,69
|
0,52
|
0,16
|
4,55
|
1,4
|
| 3,6
|
1,4
|
0,5
|
1,96
|
0,7
|
0,25
|
5,04
|
1,8
|
| 31,4
|
13,2
|
6,9
|
17,64
|
9,38
|
5,33
|
41,63
|
21,63
|
Линейная модель множественной регрессии имеет вид:
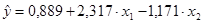
Если объем капиталовложений увеличить на 1 млн. руб., то выручка предприятия увеличиться в среднем на 2,317 млн. руб. при неизменных размерах основных производственных фондов.
Если основные производственные фонды увеличить на 1 млн. руб., то выручка предприятия уменьшиться в среднем на 1,171 млн. руб. при неизменном объеме капиталовложений.
3.
РАССЧИТАЕМ:
коэффициент множественной корреляции:

Связь выручки предприятия с объемом капиталовложений и основными производственными фондами тесная.
коэффициент детерминации:

67,82% изменения выручки предприятия обусловлено изменением объема капиталовложений и основных производственных фондов, на 32,18% - влиянием факторов, не включенных в модель.
F – критерий Фишера
Проверим значимость уравнения

Табличное значение F – критерия при уровне значимости α = 0,05 и числе степеней свободы d.f.1
= k = 2 (количество факторов), числе степеней свободы d.f.2
= (n – k – 1) = (10 – 2 – 1) = 7 составит 4,74.
Так как Fрасч.
= 7,375 > Fтабл.
= 4.74, то уравнение регрессии в целом можно считать статистически значимым.
Рассчитанные показатели можно найти в среде Excel с помощью надстройки АНАЛИЗА ДАННЫХ, инструмента РЕГРЕССИЯ.
Таблица 11
Вспомогательные вычисления для нахождения средней относительной ошибки аппроксимации
| y
|
x1
|
x2
|
yрасч
.
|
y-yрасч
|
А
|
| 3,0
|
1,1
|
0,4
|
2,97
|
0,03
|
0,010
|
| 2,9
|
1,1
|
0,4
|
2,97
|
-0,07
|
0,024
|
| 3,0
|
1,2
|
0,7
|
2,85
|
0,15
|
0,050
|
| 3,1
|
1,4
|
0,9
|
3,08
|
0,02
|
0,007
|
| 3,2
|
1,4
|
0,9
|
3,08
|
0,12
|
0,038
|
| 2,8
|
1,4
|
0,8
|
3,20
|
-0,40
|
0,142
|
| 2,9
|
1,3
|
0,8
|
2,96
|
-0,06
|
0,022
|
| 3,4
|
1,6
|
1,1
|
3,31
|
0,09
|
0,027
|
| 3,5
|
1,3
|
0,4
|
3,43
|
0,07
|
0,019
|
| 3,6
|
1,4
|
0,5
|
3,55
|
0,05
|
0,014
|
| |
|
|
|
|
0,353
|
среднюю относительную ошибку аппроксимации
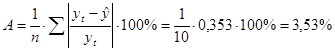
В среднем расчетные значения отличаются от фактических на 3,53 %. Ошибка небольшая, модель можно считать точной.
4.
Построить степенную модель множественной регрессии 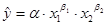
Для построения данной модели прологарифмируем обе части равенства
lg y = lg a + β1
∙ lg x1
+ β2
∙ lg x2
.
Сделаем замену Y = lg y, A = lg a, X1
= lg x1
, X2
= lg x2
.
Тогда Y = A + β1
∙ X1
+ β2
∙ X2
– линейная двухфакторная модель регрессии. Можно применить МНК.
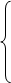 
Расчеты представлены в таблице 12.
 
Таблица 12
Вспомогательные вычисления для нахождения параметров степенной модели множественной регрессии
| y
|
x1
|
x2
|
lg x1
|
lg x2
|
lg y
|
lg2
x1
|
lg x1
*
lg x2
|
lg y*lg x1
|
lg2
x2
|
lg y*
lg x2
|
| 3,0
|
1,1
|
0,4
|
0,041
|
-0,398
|
0,477
|
0,002
|
-0,016
|
0,020
|
0,158
|
-0,190
|
| 2,9
|
1,1
|
0,4
|
0,041
|
-0,398
|
0,462
|
0,002
|
-0,016
|
0,019
|
0,158
|
-0,184
|
| 3,0
|
1,2
|
0,7
|
0,079
|
-0,155
|
0,477
|
0,006
|
-0,012
|
0,038
|
0,024
|
-0,074
|
| 3,1
|
1,4
|
0,9
|
0,146
|
-0,046
|
0,491
|
0,021
|
-0,007
|
0,072
|
0,002
|
-0,022
|
| 3,2
|
1,4
|
0,9
|
0,146
|
-0,046
|
0,505
|
0,021
|
-0,007
|
0,074
|
0,002
|
-0,023
|
| 2,8
|
1,4
|
0,8
|
0,146
|
-0,097
|
0,447
|
0,021
|
-0,014
|
0,065
|
0,009
|
-0,043
|
| 2,9
|
1,3
|
0,8
|
0,114
|
-0,097
|
0,462
|
0,013
|
-0,011
|
0,053
|
0,009
|
-0,045
|
| 3,4
|
1,6
|
1,1
|
0,204
|
0,041
|
0,531
|
0,042
|
0,008
|
0,108
|
0,002
|
0,022
|
| 3,5
|
1,3
|
0,4
|
0,114
|
-0,398
|
0,544
|
0,013
|
-0,045
|
0,062
|
0,158
|
-0,217
|
| 3,6
|
1,4
|
0,5
|
0,146
|
-0,301
|
0,556
|
0,021
|
-0,044
|
0,081
|
0,091
|
-0,167
|
| 31,4
|
13,2
|
6,9
|
1,178
|
-1,894
|
4,955
|
0,163
|
-0,165
|
0,592
|
0,614
|
-0,943
|
Решаем систему уравнений применяя метод Крамера.
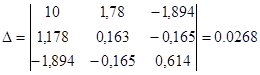 
 
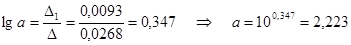
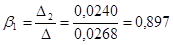 
Степенная модель множественной регрессии имеет вид:

В степенной функции коэффициенты при факторах являются коэффициентами эластичности. Коэффициент эластичности показывает на сколько процентов измениться в среднем значение результативного признака у, если один из факторов увеличить на 1 % при неизменном значении других факторов.
Если объем капиталовложений увеличить на 1%, то выручка предприятия увеличиться в среднем на 0,897% при неизменных размерах основных производственных фондов.
Если основные производственные фонды увеличить на 1%, то выручка предприятия уменьшиться на 0,226% при неизменных капиталовложениях.
5.
РАССЧИТАЕМ:
коэффициент множественной корреляции:

Связь выручки предприятия с объемом капиталовложений и основными производственными фондами тесная.
Таблица 13
Вспомогательные вычисления для нахождения коэффициента множественной корреляции, коэффициента детерминации, ср.относ.ошибки аппроксимации степенной модели множественной регрессии
| Y
|
X1
|
X2
|
Y расч.
|
(Y-Yрасч
.)2
|
(Y-Yср
)2
|
A
|
| 3,0
|
1,1
|
0,4
|
2,978
|
0,000
|
0,020
|
0,007
|
| 2,9
|
1,1
|
0,4
|
2,978
|
0,006
|
0,058
|
0,027
|
| 3,0
|
1,2
|
0,7
|
2,838
|
0,026
|
0,020
|
0,054
|
| 3,1
|
1,4
|
0,9
|
3,079
|
0,000
|
0,002
|
0,007
|
| 3,2
|
1,4
|
0,9
|
3,079
|
0,015
|
0,004
|
0,038
|
| 2,8
|
1,4
|
0,8
|
3,162
|
0,131
|
0,116
|
0,129
|
| 2,9
|
1,3
|
0,8
|
2,959
|
0,003
|
0,058
|
0,020
|
| 3,4
|
1,6
|
1,1
|
3,317
|
0,007
|
0,068
|
0,024
|
| 3,5
|
1,3
|
0,4
|
3,460
|
0,002
|
0,130
|
0,012
|
| 3,6
|
1,4
|
0,5
|
3,516
|
0,007
|
0,212
|
0,023
|
| 31,4
|
13,2
|
6,9
|
|
0,198
|
0,684
|
0,342
|
коэффициент детерминации:

71,06% изменения выручки предприятия в степенной модели обусловлено изменением объема капиталовложений и основных производственных фондов, на 28,94 % - влиянием факторов, не включенных в модель.
F – критерий Фишера
Проверим значимость уравнения

Табличное значение F – критерия при уровне значимости α = 0,05 и числе степеней свободы d.f.1
= k = 2, числе степеней свободы d.f.2
= (n – k – 1) = (10 – 2 – 1) = 7 составит 4,74.
Так как Fрасч.
= 8,592 > Fтабл.
= 4.74, то уравнение степенной регрессии в целом можно считать статистически значимым.
среднюю относительную ошибку аппроксимации

В среднем в степенной модели расчетные значения отличаются от фактических на 3,42 %. Ошибка небольшая, модель можно считать точной.
6.
СОСТАВИМ СВОДНУЮ ТАБЛИЦУ ВЫЧИСЛЕНИЙ (табл. 14)
Таблица 14
| Параметры
|
Модель
|
| линейная
|
степенная
|
| 
|

|
| Коэффициент множественной
корреляции
|
0,8235
|
0,8429
|
| Коэффициент
детерминации
|
0,6782
|
0,7106
|
| F – критерий
Фишера
|
7,375
|
8,592
|
| Средняя
относительная ошибка
аппроксимации, %
|
3,53
|
3,42
|
В целом модели имеют примерно одинаковые характеристики. Но лучшей считается степенная модель, т.к значение коэффициента корреляции, индекса детерминации, F – критерия Фишера немного больше, а средняя относительная ошибка аппроксимации немного меньше, чем у линейной модели.
7.
НАЙДЕМ ЧАСТНЫЕ КОЭФФИЦИЕНТЫ ЭЛАСТИЧНОСТИ И β – КОЭФФИЦИЕНТЫ
Для нахождения частных коэффициентов эластичности составим частные уравнения регрессии, т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором х при закреплении других учитываемых во множественной регрессии на среднем уровне.
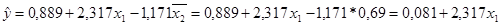



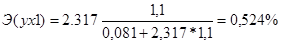
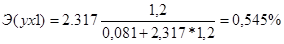


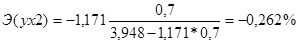 и т.д. и т.д.
Результаты расчетов представлены в таблице 15.
Таблица 15
Вспомогательная таблица для вычисления частных коэффициентов эластичности
| Y
|
X1
|
X2
|
Э(ух1)
|
Э(ух2)
|
| 3,0
|
1,1
|
0,4
|
0,524
|
-0,135
|
| 2,9
|
1,1
|
0,4
|
0,524
|
-0,135
|
| 3,0
|
1,2
|
0,7
|
0,545
|
-0,262
|
| 3,1
|
1,4
|
0,9
|
0,583
|
-0,364
|
| 3,2
|
1,4
|
0,9
|
0,583
|
-0,364
|
| 2,8
|
1,4
|
0,8
|
0,583
|
-0,311
|
| 2,9
|
1,3
|
0,8
|
0,565
|
-0,311
|
| 3,4
|
1,6
|
1,1
|
0,615
|
-0,484
|
| 3,5
|
1,3
|
0,4
|
0,565
|
-0,135
|
| 3,6
|
1,4
|
0,5
|
0,583
|
-0,174
|
Бета коэффициент рассчитываем по формуле:

 - среднее квадратическое отклонение. - среднее квадратическое отклонение.
Необходимые вычисления для расчета СКО представлены в таблице 9.
 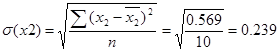
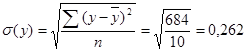

Если объем капиталовложений увеличить на величину своего СКО, т.е. 0,147 млн. руб., то выручка предприятия увеличится на 1,302 величины своего СКО, т.е. на 1,302 * 0,262 = 0,341 млн. руб.
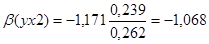
Если основные производственные фонды увеличить на величину своего СКО, т.е. на 0,239 млн. руб., то выручка предприятия уменьшится на 1,068 своего СКО, т.е. на 1,068 * 0,262 = 0,280 млн. руб.
8.
ПО ЛИНЕЙНОЙ МОДЕЛИ РЕГРЕССИИ СДЕЛАЕМ ПРОГНОЗ НА СЛЕДУЮЩИЕ ДВА ГОДА показателя у (выручка), в зависимости от х1
(объема капиталовложений) и х2
(основных производственных фондов).
Прогнозные значения факторов можно получить, используя метод прогнозирования с помощью среднего абсолютного прироста:
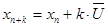 , ,
где  - средний абсолютный прирост, рассчитываемый по формуле: - средний абсолютный прирост, рассчитываемый по формуле:
 ; ;
k – период упреждения;
n – количество наблюдений.
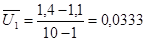 , тогда , тогда
Х1, 11
= 1,4 + 1 ∙ 0,0333 = 1,4333 (млн.руб.)
Х1, 12
= 1,4 + 2 ∙ 0,0333 = 1,4667(млн.руб.)

Х2, 11
= 0,5 + 1 ∙ 0,0111 = 0,5111
Х2, 12
= 0,5 + 2 ∙0,0111 = 0,5222
Составляем вектор прогнозных значений факторов:

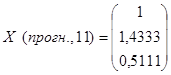 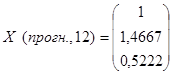 . .
Вычислим точечные прогнозы поведения выручки предприятия на моменты времени t = 11 и t = 12. Для этого подставим прогнозные значения факторов в уравнение регрессии.
 (млн. руб.) (млн. руб.)
 (млн. руб.) (млн. руб.)
Для получения интервального прогноза  рассчитываем доверительные интервалы, используя величину отклонения от линии регрессии (U): рассчитываем доверительные интервалы, используя величину отклонения от линии регрессии (U):
 , ,

 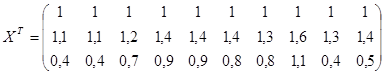
Операции с матрицами осуществим в среде Excel с помощью встроенных математических функций МУНОЖ и МОБР.
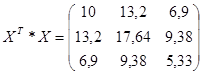 


Среднее квадратическое отклонение расчетных значений от фактических:

Коэффициент Стьюдента tα
для m = 10 – 2 – 1 = 7 степеней свободы и уровня значимости α = 0,05 равен 2,36.
U(11) = 0,1773 ∙ 2.36 ∙ 0,61610,5
= 0,329
U(11) = 0,1773 ∙ 2.36 ∙ 0.74810,5
= 0,362
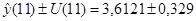

Результаты вычислений представим в виде таблицы.
Таблица 16
| Шаг
|
Точечный прогноз,
млн. руб.
|
Нижняя граница,
млн. руб.
|
Верхняя граница,
млн. руб.
|
| 11
|
3,6121
|
3,2829
|
3,9412
|
| 12
|
3,6763
|
3,3136
|
4,0390
|
Список литературы:
1. Доугерти К. Введение в эконометрику. – М.: Инфра – М, 2001. – 402 с.
2. Катышев П. К., Пересецкий А. А. Сборник задач к начальному курсу эконометрики. – М.: Дело, 1999. – 72 с.
3. Практикум по эконометрике: Учеб. пособие; Под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2001. – 192 с.
4. Тутыгин А.Г., Амбросевич М.А., Третьяков В.И. Эконометрика. Краткий курс лекций. Учебное пособие. – М.-Архангельск, Издательский дом «Юпитер», 2004. – 54 с.
5. Эконометрика: Учеб. пособие; Под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2001. –245 с.
|