| Задача 1.
Задача об оптимальном использовании ограниченных ресурсов.
Продукцией городского молочного завода являются молоко, кефир и сметана. На производство 1 т молока, кефира и сметаны требуется соответственно 1,01; 1,01; и 9,45 т молока. При этом затраты рабочего времени при разливе 1 т молока и кефира составляют 0,18 и 0,19 машиночаса. На расфасовке 1 т сметаны заняты специальные автоматы в течение 3,25 ч. Всего для производства цельномолочной продукции завод может использовать 136 т молока. Основное оборудование может быть занято в течение 21,4 машиночасов, а автоматы по расфасовке сметаны – в течение – в течение 16,25 ч. Прибыль от реализации 1 т молока, кефира и сметаны соответственно равна 30,22 и 136 руб. завод должен ежедневно производить не менее 100 т молока.
Требуется определить объемы выпуска молочной продукции, позволяющие получить наибольшую прибыль. К чему приведет задание по выпуску кефира в объеме не менее 10 т?
На основе исходных данных составим таблицу 1.
Таблица 1.
| Ресурсы
|
Нормы расхода ресурсов на единицу изделия, т
|
Наличие ресурсов, т
|
| молоко
|
кефир
|
сметана
|
| молоко
|
1,01
|
1,01
|
9,45
|
136
|
| машиночасы
|
0,18
|
0, 19
|
21,4
|
| автомат-часы
|
3,25
|
16,25
|
| Прибыль
|
30
|
22
|
136
|
| Выпуск, т
|
Не менее 100
|
Составим экономико-математическую модель задачи.
Обозначим через Х1, Х2, Х3 объемы производства соответствующего вида продукции, соответственно молоко, кефир, сметана.
Целевая функция – это математическая запись критерия оптимальности, т.е. выражение, которое необходимо макcимизировать f(x) = 30Х1 + 22Х2 + 136Х3.
Ограничения по ресурсам:
1,01Х1 + 1,01Х2 + 9,45Х3 ≤ 136
0,18Х1 + 0, 19Х2 ≤ 21,4
3,25Х3 ≤ 16,25
Х1 ≥ 100
Х1, Х2, Х3 ≥ 0.
Решение.
Приведем подробное описание технологии получения решения приведенной ЗЛП.
Обозначим: М1 – один щелчок левой кнопкой мыши;
М2 – двойной щелчок левой кнопкой мыши.
Прежде чем приступить к решению задачи студенту необходимо на сервере создать папку под своим именем. Порядок работы:
На рабочем столе найдите пиктограмму "Сетевое окружение" → М1;
Двойным щелчок мыши открывайте пиктограмму "Для документов".
Двойным щелчком мыши открывайте пиктограмму "Для студентов".
В папке с фамилией ведущего преподавателя создайте папку под своей фамилией.
Далее необходимо последовательно выполнить следующую работу:
1. Создать форму для ввода условий задачи. Запустите Excel, выбрав Microsoft Excel из подменю программы главного меню Windows. Открывается чистый лист Excel. Создайте текстовую форму – таблицу для ввода условий задачи. (рис.1.1)

Рис.1.1

Рис.1.2
2 Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Обозначьте через Х1, Х2, Х3 количество молочной продукции каждого типа. В нашей задаче оптимальные значения компонент вектора Х = (Х1, Х2, Х3) будут помещены в ячейках B3: D3, оптимальное значение целевой функции - в ячейке Е4.
3. Ввести исходные данные задачи в созданную форму – таблицу, представленную на рис.1.2.
Порядок составления таблицы следующий.
В строке Меню указатель мыши на имя Файл → М1. В развернутом меню команда Сохранить как → М1. Появляется диалоговое окно Сохранение документа. Путем перебора папок в строке Папка должна быть установлена папка с фамилией студента. Далее курсор переведите в строку Имя файла и присвойте ему имя. Далее нажать кнопку Сохранить.
4. Ввести зависимость для целевой функции:
Курсор в ячейку Е4.
Курсор на кнопку "Мастер функций", расположенную на панели инструментов.
М1. На экране появится диалоговое окно Мастер функций шаг 1 из 2 (Рис.1.3).

Рис.1.3.

Рис.1.4.
Курсор в окно "Категория" на категорию Математические;
М1;
Курсор в окно Функции на СУММПРОИЗВ;
М1. На экране появляется диалоговое окно СУММПРОИЗВ (Рис.1.4);
В строку "Массив 1" ввести B$3: D$3;
В строку "Массив 2" ввести В4: Е4;
Кнопка "ОК". На экране: в ячейку Е4 введена функция (Рис.1.5).

Рис.1.5.
5 Ввести зависимости для ограничений:
Курсор в ячейку Е4;
На панели инструментов кнопка Копировать в буфер → М1;
Курсор в ячейку Е7;
На панели инструментов кнопка Вставить из буфера → М1;
Курсор в ячейку Е8;
На панели инструментов кнопка Вставить из буфера → М1;
Курсор в ячейку Е9;
На панели инструментов кнопка Вставить из буфера → М1;
Курсор в ячейку Е10;
На панели инструментов кнопка Вставить из буфера → М1 (Рис.1.5.1).

Рис.1.5.1.
В строке Меню указатель мыши на Поиск решения → М1. Появляется диалоговое окно Поиск решения. (рис.1.6).

Рис.1.6.
6. Назначить целевую функцию (установить целевую ячейку):
Курсор в строку Установить целевую ячейку;
Введите адрес ячейки $E$4;
Введите направление целевой функции в зависимости от условия вашей задачи – максимальному значению или минимальному значению;
Курсор в строку изменяя ячейки;
Введите адреса искомых переменных: B$3: D$3.
7. Ввести ограничения:
Указатель мыши на кнопку Добавить → М1. Появляется диалоговое окно Добавление ограничения (Рис.1.7)
В строке ссылка на ячейку введите адрес $E$7;
Введите знак ограничения ≤;
В строке ограничение введите адрес $G$7;
Указатель мыши на кнопку Добавить → М1. На экране вновь появится диалоговое окно Добавление ограничения (Рис.1.7).
Введите остальные ограничения задачи по вышеописанному алгоритму;
Поле введения последнего ограничения кнопка ОК.

Рис.1.7.
На экране появится Поиск решения с введенными условиями (Рис.1.8).

Рис.1.8.
8. Ввести параметры решения ЗЛП:
В диалоговом окне указатель мыши на кнопку Параметры. На экране появляется диалоговое окно Параметры поиска решения (Рис.1.9).

Рис.1.9.
Установите флажки в окнах Линейная модель (это обеспечит применение симплекс-метода) и Неотрицательные значения;
Указатель мыши на кнопку ОК. на экране появится диалоговое окно Поиск решения;
Указатель мыши на кнопку Выполнить.
Через непродолжительное время появится диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками B3: D3 для значений Xi и ячейка Е4 с максимальным значением целевой функции (Рис.1.10).


Рис.1.10.
Полученное решение означает, что максимальный доход 3795,81 руб. городской молочный завод может получить при выпуске и реализации 118,89 тонн молока и 1,68 тонн сметаны. При этом ресурсы молоко и машиночасы будут использованы полностью, а автомат-часы будут использованы только 5,48 из 16,25 ч. При таком плане выпуска молочной продукции выполнится условие ежедневного выпуска молока не менее 100 тонн.
9. Для того, чтобы определить к чему приведет задание по выпуску кефира в объеме не менее 10 т при существующих условиях задачи введем дополнительно еще одно ограничение по выпуску кефира.
Таблица с данными изменится (рис.1.11)

Рис.1.11.
Добавим ограничение по выпуску кефира (Рис.1.12):

Рис. .1.12.
Нажмем ОК и в появившемся диалоговом окне Поиск решения нажмем Выполнить и сохраним найденные значения (Рис.1.13).
Рис.1.13.
Через непродолжительное время появится диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками B3: D3 для значений Xi и ячейка Е4 с максимальным значением целевой функции (Рис.1.14).

Рис.1.14.
Полученное решение означает, что максимальный доход 3707,81 руб. городской молочный завод может получить при выпуске и реализации 108,33 тонн молока, 10 тонн кефира 1,74 тонн сметаны. При этом ресурсы молоко и машиночасы будут использованы полностью, а автомат-часы будут использованы только 5,67 из 16,25 ч. При таком плане выпуска молочной продукции выполнится условие ежедневного выпуска молока не менее 100 тонн и кефира не менее 10 тонн.
Задача 2.
Администрация деревообрабатывающего предприятия "Смена" приняла на работу пять человек. Каждый из них имеет различные способности и навыки и затрачивает различное время на выполнение определенной работы. В настоящее время необходимо выполнить пять видов работ. Время выполнения работы каждым работником приведено в таблице.
Таблица 2.1.
| Работник
|
Время выполнения, ч
|
| Работа 1
|
Работа 2
|
Работа 3
|
Работа 4
|
Работа 5
|
| Р1
|
25
|
16
|
15
|
14
|
13
|
| Р2
|
25
|
17
|
18
|
23
|
15
|
| Р3
|
30
|
15
|
20
|
19
|
14
|
| Р4
|
27
|
20
|
22
|
25
|
12
|
| Р5
|
29
|
19
|
17
|
32
|
10
|
1. Требуется назначить на каждый вид работы одного из работников. Как это следует сделать, чтобы общее время, необходимое для завершения всех видов работ, было минимальным?
2. Предприятие "Смена" может принять на работу еще одного рабочего по совместительству, который выполняет каждую работу в течение следующего времени.
Таблица 2.2.
| Работник – совместитель
|
Время выполнения, ч
|
| Работа 1
|
Работа 2
|
Работа 3
|
Работа 4
|
Работа 5
|
| Р6
|
28
|
16
|
19
|
16
|
15
|
Требуется определить, каким образом данная мера повлияет на назначение рабочих и минимизацию общего времени выполнения работ.
Одним из условий поставленной задачи является минимизация общего времени выполнения работ.
Решение.
Экономико-математическая модель задачи
Переменные:

Целевая функция – суммарное время, необходимое для завершения всех видов работ, которое необходимо минимизировать:
f(x) = 25x11 + 16x12 + 15x13 + 14x14 + 13x15 + 25x21 + 17x22 + 18x23 + 23x24 + 15x25 + 30x31 + 15x32 + 20x33 + 19x34 + 14x35 + 27x41 + 20x42 + 22x43 + 25x44 + 12x45 + 29x51 + 19x52 + 17x53 + 32x54 + 10x55 → min.
Функциональные ограничения:
по работам

по работникам
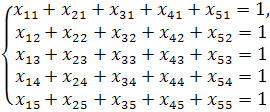
Прямые ограничения:
хij ≥0.
Значения переменных хij располагаются в блоке ячеек B13: F17, в ячейку G18 введена формула для вычисления целевой функции (рис.2.1)

Рис.2.1.
Введены формулы для вычисления ограничений по работам:
=СУММ(B13: F13)
=CУММ(B14: F14)
=СУММ(B15: F15)
=СУММ(B16: F16)
=СУММ(B17: F17)
=СУММПРОИЗВ(B4: F8,B13: F17).
Аналогично вводятся формулы для вычислений ограничений по работникам. На рис.2.2. заполнены все поля Поиска решений.

Рис 2.2.
В группе Ограничения заданы, помимо остальных, ограничения на двоичность переменных (первая запись), означающие, что значение xij должно быть 0 или 1. Добавляя ограничения, следует выбрать опцию двоичное в раскрывшемся списке Ограничение.
В результате решения будет получен ответ на первый вопрос задачи (рис.2.3).

Рис.2.3.
Чтобы получить ответ на второй вопрос задачи, необходимо добавить ограничение по шестому работнику и в ограничениях по работникам знак = заменить на знак ≤ (рис.2.4).

Рис.2.4.
Выводы:
1. Общее время, необходимое для завершения всех видов работ, равно 83 ч. Закрепление работников за работами приведено на рис.2.3, т.е. работник Р1 будет назначен на работу 4, работник Р2 на работу 1, работник Р3 на работу 2, работник Р4 на работу 5, работник Р5 на работу 3.
2. Прием на работу работника Р6 приведет к изменению назначений работников на работы и позволит снизить общее время, необходимое для завершения всех видов работ, до 81 ч, но при этом работник Р4 должен быть уволен или отправлен в отпуск (см. рис.2.4).
|