| МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГОУ ВПО «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ
АГРАРНЫЙ УНИВЕРСИТЕТ ИМЕНИ К. Д. ГЛИНКИ»
Контрольная работа
по дисциплине
«
Экономико-математическое моделирование
»
Тема: Экономико-математическая задача по оптимизации рационов кормления
Выполнил: студент Б-3с
заочного отделения
Экономического факультета
Михайлова Е.А.
Шифр 08053
ВОРОНЕЖ
2010
1 Постановка задачи
Для повышения продуктивности животных необходимо их полноценное кормление. Недостаток какого-либо питательного вещества в рационе животных ведет к снижению их продуктивности, а неполноценное кормление может вызывать перерасход кормов. Поэтому кормовой рацион должен быть полностью сбалансирован по всем питательным веществам, необходимых для каждого вида животных.
Постановку данной задачи можно сформулировать следующим образом. Из имеющихся в хозяйстве кормов для заданной группы скота составить рацион кормления при определенном уровне продуктивности, который должен полностью удовлетворять биологические потребности животных по содержанию в нем питательных веществ, соответствовать зоотехническим требованиям по пределам включения в него различных групп кормов и иметь наименьшую себестоимость.
2 Подготовка входной информации.
Для разработки экономико-математической модели данной задачи необходимо подготовить следующую информацию:
· наличие кормов по видам;
· содержание питательных веществ в единице корма;
· требуемое количество питательных веществ в рационе;
· максимально и минимально возможные нормы скармливания отдельных видов кормов;
· себестоимость кормов или цены приобретения.
Необходимо рассчитать оптимальный суточный рацион кормления молодняка крупного рогатого скота на откорме. В хозяйстве имеются следующие корма: ячмень дробленый, отруби пшеничные, горох, витаминно-травяная мука, солома, сено, сенаж, силос кукурузный. Можно приобрести следующие покупные корма: комбикорм, жом, патоку, минерально-витаминный премикс. Питательность 1 кг корма приведена в таблице 1.
Нормы кормления молодняка крупного рогатого скота на откорме на 1 голову в сутки по вариантам приводится в таблице 2.
Таблица 1
. Питательность 1 килограмма корма
| Питательное вещество
|
Отруби пшеничные
|
Ячмень дробленый
|
Горох
|
Комбикорм
|
Витаминно-травяная мука
|
Сено
|
Солома
|
Сенаж
|
Силос
|
Жом
|
Патока
|
Премикс
|
| Кормовые единицы
|
0,75
|
1,15
|
1,18
|
1,0
|
0,63
|
0,48
|
0,34
|
0,32
|
0,2
|
0,12
|
0,76
|
0,5
|
| Обменная энергия, мДж
|
8,85
|
10,5
|
11,1
|
9,1
|
8,01
|
6,45
|
5,71
|
3,68
|
2,3
|
1,13
|
9,36
|
| Сухое вещество, кг
|
0,85
|
0,85
|
0,85
|
0,88
|
0,9
|
0,83
|
0,83
|
0,45
|
0,25
|
0,112
|
0,8
|
| Сырой протеин, г
|
151
|
113
|
218
|
165
|
99
|
91
|
49
|
54
|
25
|
12
|
99
|
| Переваримый протеин, г
|
97
|
27
|
192
|
110
|
42
|
51
|
13
|
38
|
14
|
6
|
60
|
55
|
| Сырая клетчатка, г
|
88
|
49
|
54
|
55
|
280
|
237
|
331
|
148
|
75
|
33
|
| Сахар, г
|
47
|
22
|
55
|
51
|
50
|
29
|
2,4
|
22
|
6
|
2,5
|
626
|
25,5
|
| Сырой жир, г
|
41
|
22
|
19
|
25
|
18
|
21
|
19
|
13
|
10
|
3
|
| Кальций, г
|
2,0
|
2,0
|
2,0
|
6,5
|
5,8
|
5,6
|
3,3
|
2,8
|
1,4
|
1,5
|
3,2
|
133,6
|
| Фосфор, г
|
9,6
|
3,9
|
4,3
|
6,0
|
3,1
|
1,3
|
0,8
|
1,4
|
0,4
|
0,14
|
0,2
|
257,3
|
| Магний, г
|
4,3
|
1,0
|
1,2
|
4,0
|
3,3
|
1,4
|
1,1
|
0,8
|
0,5
|
0,5
|
0,1
|
11
|
| Каротин, мг
|
2,6
|
0,2
|
0,2
|
120
|
24
|
4
|
30
|
20
|
| Кобальт, мг
|
0,1
|
0,26
|
0,18
|
0,2
|
0,66
|
0,2
|
0,14
|
0,39
|
0,02
|
0,06
|
0,6
|
0,5
|
| Витамин Е, мг
|
20,9
|
50
|
53
|
35
|
75
|
300
|
45
|
46
|
3,0
|
85
|
| Соль, грамм
|
81
|
Таблица 2
. Нормы кормления молодняка крупного рогатого скота на откорме на 1 голову в сутки
| Питательное вещество
|
Показатели
|
| Кормовые единицы
|
6,2
|
| Обменная энергия,мДж
|
54
|
| Сухое вещество,кг
|
6
|
| Сырой протеин,г
|
905
|
| Переваримый протеи ,г
|
590
|
| Сырая клетчатка,г
|
1260
|
| Сахар,г
|
470
|
| Сырой жир,г
|
235
|
| Кальций,г
|
31
|
| Фосфор,г
|
18
|
| Магний,г
|
14
|
| Каротин,мг
|
115
|
| Кобальт,мг
|
3,6
|
| Витамин Е,мг
|
150
|
| Соль,г
|
20
|
На основании научно обоснованных типов кормления животных и возможностей хозяйства отдельные группы и виды кормов могут содержаться в рационе в определенном количестве. Предельные нормы скармливания по группам кормов приводятся в таблице 3.
Данные о себестоимости и ценах приобретения кормов и кормовых добавок приведены в таблице 4.
Таблица 3
Минимальное и максимальное содержание отдельных видов и групп кормов в рационе
| Виды и группы кормов
|
Показатели
|
| Концентраты, % min
|
20
|
| max
|
31
|
| Грубые, % min
|
10
|
| max
|
25
|
| Силос, % min
|
12
|
| max
|
23
|
| Жом, % min
|
18
|
| max
|
30
|
| Сенаж, % min
|
9
|
| max
|
19
|
| Патока, кг max
|
2,3
|
| ВТМ, кг max
|
1,2
|
| Силос, кг max
|
26
|
| Комбикорм в % от концентратов
|
37
|
| Сено в % от грубых
|
39
|
Таблица 4
Себестоимость и цена приобретения кормов и кормовых добавок, руб/кг
| Виды корма
|
Показатели
|
| Отруби пшеничные
|
22
|
| Ячмень дробленый
|
19
|
| Горох
|
18
|
| Комбикорм
|
38
|
| ВТМ
|
24
|
| Сено
|
20
|
| Солома
|
1,8
|
| Сенаж
|
1,2
|
| Силос
|
1,3
|
| Жом
|
3,4
|
| Патока
|
19
|
| Премикс
|
42
|
3 Построение экономико-математической модели
За основные неизвестные в данной задаче принимается количество кормов и кормовых добавок, включаемых в суточный рацион,
X1 - отруби пшеничные
X2 - ячмень дробленый
Х3 - горох
X4 - комбикорм
X5 - витаминно-травяная мука
X6 - сено
X7 - солома
X8 - сенаж
X9 - силос кукурузный
X10 - жом
X11 - патока
X12 - премикс минерально-витаминный
Вспомогательная переменная X13 выражает общее содержание кормовых единиц в рационе, За единицу измерения основных переменных величин принят физический вес корма в килограммах (кг).
На переменные накладываются следующие группы ограничений:
· по содержанию питательных веществ в рационе;
· по пределам включения отдельных групп кормов в рацион;
· по соотношению отдельных видов кормов и добавок;
· по суммарному количеству кормовых единиц в рационе.
Основными ограничениями (1-15)
являются условия по балансированию питательных веществ в рационе.
Технико-экономическими коэффициентами при основных переменных Xj в этих ограничениях являются показатели содержания питательных веществ в единице каждого вида корма (Таблица 1), а в правой части неравенств записывается потребное количество каждого вида питательных веществ для животных, необходимое для получения определенной продуктивности - B
i
(Таблица 2).
Например, ограничение, требующее наличия в рационе 5,3 кормовых единиц, будет записано в следующем виде:
0,75x1+1,15x2+…….+0,76x11+0,5x12>=6,2 (1)
Ограничение по содержанию обменной энергии в рационе
8,85x1+10,5x2+……,+9,36x11>=54(2)
Ограничение по содержанию сухого вещества в рационе
0,85x1+0,85x2……+0,8x11>=6(3)
Ограничение по содержанию сырого протеина в рационе
151x1+113x2+…,,+99x11>=905(4)
Ограничение по содержанию переваримого протеина в рационе
97x1+27x2+……+60x11+ 55x12>=590(5)
Ограничение по содержанию сырой клетчатки в рационе
88x1+49x2+……+33x10>=1260(6)
Ограничение по содержанию сахара в рационе
47x1+22x2+……+626x11+25,5x12>=470(7)
Ограничение по содержанию сырого жира в рационе
41x1+22x2+……+3x10>=235(8)
Ограничение по содержанию кальция в рационе
2x1+2x2+……+3,2x11+133,6x12>=31(9)
Ограничение по содержанию фосфора в рационе
9,6x1+3,9x2+……+0,2x11+257,3x12>=18(10)
Ограничение по содержанию магния в рационе
4,3x1+1x2+……+0,1x11+27x12>=14(11)
Ограничение по содержанию каротина в рационе
2,6x1+0,2x2+……+20x9>=115(12)
Ограничение по содержанию кобальта в рационе
0,1x1+0,26x2+……+0,06x10+0,6x11+0,5x12>=3,6(13)
Ограничение по содержанию витамина Е в рационе
20,9x1+50x2+……+3x11>=150(14)
Ограничение по содержанию соли в рационе
81x12>=20(15)
Дополнительные ограничения (16-25)
по пределам скармливания отдельных видов кормов или групп кормов.
Условие по минимальному и максимальному удельному весу концентратов в рационе имеет вид:
минимальная граница
(границы выбираются из таблицы 3 и делятся на 100 и записываются в виде коэффициента при х13) (при x4 – коэффициент 1, в данной записи его не пишут),
(не менее 20%/100=0,2
) 0,75x1+1,15x2+1,18x3+x4>=0,2
x13;
максимальная граница
(не более 31 %/100=0,31
) 0,75x1+1,15x2+1,18x3+x4<=0,31
x13,
Исходя из этого, преобразуя неравенство (перенесем х13 за знак неравенства), получим следующую запись данных ограничений:
0,75x1+1,15x2+1,18x3+x4-0,2
x13>=0 ;(16)
0,75x1+1,15x2+1,18x3+x4-0,31
x13<=0,
для приведения неравенства к типу «>=», преобразуем его в следующий вид
-0,75x1-1,15x2-1,18x3-x4+0,31
x13>=0(17)
Ограничение по минимальному и максимальному включению в рацион грубых кормов:
0,48x6+0,34x7-0,
1
0
x13>=0(18)
-0,48x6-0,34x7+0,25
x13>=0(19)
Ограничение по минимальному и максимальному включению в рацион силоса:
0,2x9-0,
1
2
x13>=0(20)
-0,2x9+0,23
x13>=0(21)
Ограничение по минимальному и максимальному включению в рацион жома:
0,12x10-0,18
x13>=0(22)
-0,12x10+0,3
x13>=0(23)
Ограничение по минимальному и максимальному включению в рацион сенажа:
0,32x8-0,09
x13>=0(24)
-0,32x8+0,19
x13>=0(25)
В данных ограничениях коэффициенты при основных неизвестных показывают содержание кормовых единиц в каждом виде корма указанной группы, а коэффициентами при вспомогательной неизвестной являются нижние и верхние границы содержания отдельных групп кормов в рационе выраженных в долях единицы,
Ограничения по максимальной суточной даче отдельных кормов (26-28)
имеют следующий вид (объем ограничений выбирается из таблицы 3):
Ограничение по максимальной суточной даче патоки (не более 2 кг).
x11<=2,3
(26)
Ограничение по максимальной суточной даче ВТМ (не более 1,8 кг).
x5<=1,2
(27)
Ограничение по максимальной суточной даче силоса (не более 30 кг).
x9<=26
(28)
Ограничения (29-30) по включению отдельных видов кормов
в состав группы кормов
формулируют с использованием алгебраических преобразований. Так, ограничение по включению комбикорма в размере не менее 37% (таблица 3) от веса концентрированных кормов первоначально имеет такую форму:
x4 >=0,37
*(0,75x1+1,15x2+1,18x3+x4),
а после преобразований оно приобретает следующий вид:
-0,37
*0,75x1-0,37
*1,15x2-0,37
*1,18x3+(1-0,37
)x4>=0;
перемножив коэффициенты, получим:
-0,278x1-0,426x2-0,437x3+0,63x4>=0(29)
Ограничение по включению сена в группу грубых кормов в размере не менее 39 % их питательности в начале будет записано так:
0,48x6 >= 0,39
*(0,48x6+0,34x7),
(0,48- 0,39
*0,48)х6- 0,39
*0,34x7>=0
а в окончательной форме, перемножив коэффициенты, получим:
0,293x6-0,133x7>=0 , (30)
Вспомогательное ограничение 31 , обеспечивающее нахождение суммарного количества кормовых единиц в рационе, изначально имеет вид :
0,75x1+1,15x2+,,,,,+0,76x11+0,5x12 = x13
а после преобразований оно приобретает следующий вид:
0,75x1+1,15x2+,,,,,+0,76x11+0,5x12 – x13=0 (31)
В данном ограничении коэффициенты при основных неизвестных показывают содержание кормовых единиц в каждом виде корма (табл. 1
), а по вспомогательной неизвестной –1
,
Целевая функция
(минимум себестоимости) представлена следующим образом:
Zmin
=22
x1+19
x2+……+3,4
x10+19
x11+42
x12
По неизвестным, обозначающим корма собственного производства, коэффициенты показывают себестоимость 1 кг корма, а по переменным, выражающим покупные корма и добавки, - цену приобретения (табл. 4).
В матричном
(развернутом) виде разработанная экономико-математическая модель представлена в таблице 5.
4 Запись экономико-математической модели в структурном виде
Целевая функция
:
 , где , где
Cj
– себестоимость или цена приобретения
j
-го вида корма;
Xj
– искомое количество
j
-го вида корма в составе суточного рациона,
Ограничения (условия)
:
1. Питательных веществ в рационе содержится не менее необходимого количества:
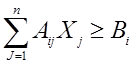 , где , где
Aij – содержание i–го питательного вещества в единице j-го вида корма;
Bi
– суточная потребность животного в i–ом питательном веществе.
2. 
Отдельные группы кормов включаются в рацион в зоотехнически обоснованных границах:
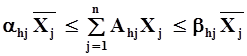 , где , где
a
hj
,
b
hj
– соответственно минимально и максимально допустимый удельный вес
h
-ой группы кормов в общей питательности рациона, выраженной в кормовых единицах;
Ahj
– содержание кормовых единиц в единице измерения
j
-го вида корма
h
- ой группы кормо.,
3. В рационе соблюдаются соотношения отдельных видов кормов и кормовых добавок
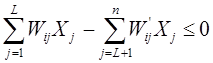 , где
, где
Wij
,
W
'
ij
–коэффициенты пропорциональности между группами кормов.
4. Вспомогательного ограничения по общему количеству кормовых единиц в единиц в рационе
 , где , где
 – суммарное количество кормовых единиц в рационе.
– суммарное количество кормовых единиц в рационе.
5. Условие неотрицательности переменных
Xj
>= 0,  >=0 >=0
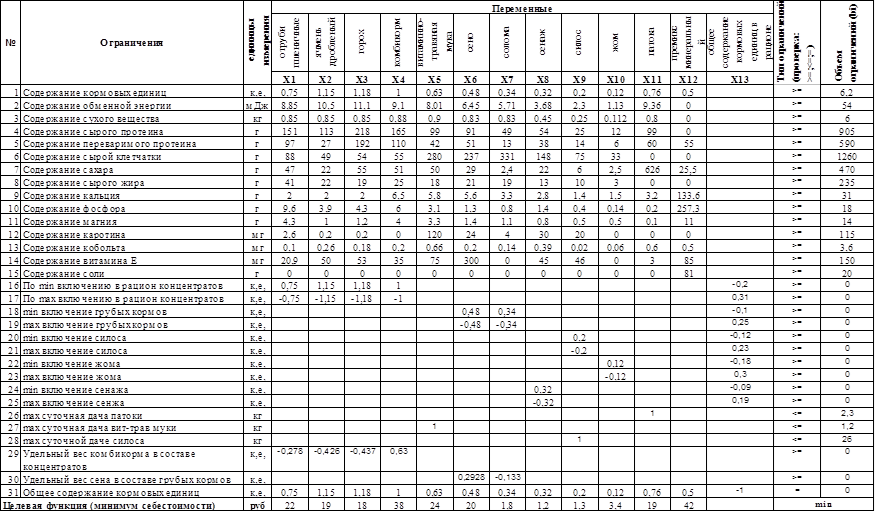
Таблица 5
Экономико-математическая модель по оптимизации рациона кормления
Дата:_________________ Подпись:____________________
|