Задача 1
В базе данных магазина, торгующего подержанными автомобилями, содержится информация об их потребительских свойствах и ценах.
Для анализа зависимости цены автомобиля Y от его возраста X1
и мощности двигателя X2
из базы данных выбраны сведения о 16 автомобилях. Эти сведения приведены в таблице 1.
Таблица 1
| Номер автомобиля i
|
Цена (тыс.у.е.) y
i
|
Возраст (лет) x
i
1
|
Мощность двигателя (л.с.) x
i
2
|
| 1
|
6,8
|
6,0
|
93
|
| 2
|
7,2
|
4,0
|
67
|
| 3
|
4,3
|
6,0
|
57
|
| 4
|
10,0
|
4,0
|
106
|
| 5
|
9,7
|
5,0
|
108
|
| 6
|
12,4
|
4,0
|
136
|
| 7
|
12,9
|
4,0
|
143
|
| 8
|
6,6
|
7,0
|
127
|
| 9
|
11,2
|
3,0
|
93
|
| 10
|
11,2
|
4,0
|
111
|
| 11
|
8,3
|
6,0
|
124
|
| 12
|
5,6
|
6,0
|
81
|
| 13
|
5,6
|
6,0
|
71
|
| 14
|
6,4
|
6,0
|
88
|
| 15
|
5,3
|
7,0
|
112
|
| 16
|
4,0
|
7,0
|
88
|
2. Множественная зависимость
С помощью коэффициентов парной корреляции проанализировать тесноту линейной связи между ценой и возрастом автомобиля, а также между ценой и мощностью двигателя. Проверить их значимость с надежностью 0,9.
Методом наименьших квадратов найти оценки коэффициентов множественной линейной регрессионной модели
 . .
Проверить статистическую значимость параметров и уравнения множественной регрессии с надежностью 0,9.
Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей возраста 3 года и мощностью двигателя 165 л.с. с доверительной вероятностью 0,95.
3. Экономическая интерпретация
На основе полученных статистических характеристик провести содержательный экономический анализ зависимости цены автомобиля от его возраста и мощности двигателя.
Расчетная таблица:
| №
|
y
|
X1
|
x2
|
x1
2
|
x2
2
|
y*x1
|
y*x2
|
y2
|
x1
x2
|
| 1
|
6,8
|
6
|
93
|
36
|
8649
|
40,8
|
632,4
|
46,2
|
558
|
| 2
|
7,2
|
4
|
67
|
16
|
4489
|
28,8
|
482,4
|
51,8
|
268
|
| 3
|
4,3
|
6
|
57
|
36
|
3249
|
25,8
|
245,1
|
18,5
|
342
|
| 4
|
10,0
|
4
|
106
|
16
|
11236
|
40,0
|
1060,0
|
100,0
|
424
|
| 5
|
9,7
|
5
|
108
|
25
|
11664
|
48,5
|
1047,6
|
94,1
|
540
|
| 6
|
12,4
|
4
|
136
|
16
|
18496
|
49,6
|
1686,4
|
153,8
|
544
|
| 7
|
12,9
|
4
|
143
|
16
|
20449
|
51,6
|
1844,7
|
166,4
|
572
|
| 8
|
6,6
|
7
|
127
|
49
|
16129
|
46,2
|
838,2
|
43,6
|
889
|
| 9
|
11,2
|
3
|
93
|
9
|
8649
|
33,6
|
1041,6
|
125,4
|
279
|
| 10
|
11,2
|
4
|
111
|
16
|
12321
|
44,8
|
1243,2
|
125,4
|
444
|
| 11
|
8,3
|
6
|
124
|
36
|
15376
|
49,8
|
1029,2
|
68,9
|
744
|
| 12
|
5,6
|
6
|
81
|
36
|
6561
|
33,6
|
453,6
|
31,4
|
486
|
| 13
|
5,6
|
6
|
71
|
36
|
5041
|
33,6
|
397,6
|
31,4
|
426
|
| 14
|
6,4
|
6
|
88
|
36
|
7744
|
38,4
|
563,2
|
41,0
|
528
|
| 15
|
5,3
|
7
|
112
|
49
|
12544
|
37,1
|
593,6
|
28,1
|
784
|
| 16
|
4,0
|
7
|
88
|
49
|
7744
|
28,0
|
352,0
|
16,0
|
616
|
| Сумма
|
127,5
|
85
|
1605
|
477
|
170341
|
630,2
|
13510,8
|
1141,9
|
8444
|
Коэффициенты парной корреляции:
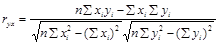 = =  = -0,833 = -0,833
 = =  = 0,665 = 0,665
Проверка значимости:
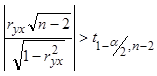
 (по таблице). (по таблице).
 = 5,63 > 1,761 = 5,63 > 1,761
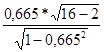 = 3,33 > 1,761 = 3,33 > 1,761
Коэффициенты корреляции существенно отличаются от 0.
Найдем матрицы:
 = = 
 = = 
Найдем матрицу  , обратную к матрице , обратную к матрице  . Определитель . Определитель
|XT
X| = 16 * 477 * 170341 + 85 * 8444 * 1605 + 1605 * 85 * 8444 – 1605 * 477 * 1605 – 85 * 85 * 170341 – 16 * 8444 * 8444 = 3692086
Алгебраические дополнения:
D11
= (–1)1 + 1
 = 477 * 170341 – 84442
= 9951521 и т.д. = 477 * 170341 – 84442
= 9951521 и т.д.
Матрица алгебраических дополнений
 = = 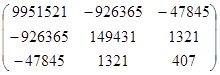
Присоединенная матрица
(XT
X)*
= DT
= 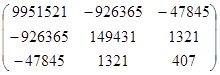 = D = D
(матрица в симметрична).
(XT
X)–1
= (XT
X)*
/ |XT
X| = 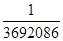  = = 
Вектор оценок коэффициентов модели:
A = (XT
X)-1
(XT
Y) =   = = 
Y = 10,455 – 1,650x1
+ 0,063x2
Расчетная таблица:
| №
|
y
|
x1
|
x2
|

|
y - 
|
(y -  )2 )2
|
y - 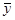
|
(y - 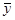 )2 )2
|
| 1
|
6,8
|
6,0
|
93,0
|
6,38
|
0,42
|
0,179
|
-1,2
|
1,4
|
| 2
|
7,2
|
4,0
|
67,0
|
8,05
|
-0,85
|
0,721
|
-0,8
|
0,6
|
| 3
|
4,3
|
6,0
|
57,0
|
4,12
|
0,18
|
0,031
|
-3,7
|
13,5
|
| 4
|
10,0
|
4,0
|
106,0
|
10,49
|
-0,49
|
0,241
|
2,0
|
4,1
|
| 5
|
9,7
|
5,0
|
108,0
|
8,97
|
0,73
|
0,539
|
1,7
|
3,0
|
| 6
|
12,4
|
4,0
|
136,0
|
12,37
|
0,03
|
0,001
|
4,4
|
19,6
|
| 7
|
12,9
|
4,0
|
143,0
|
12,81
|
0,09
|
0,009
|
4,9
|
24,3
|
| 8
|
6,6
|
7,0
|
127,0
|
6,86
|
-0,26
|
0,065
|
-1,4
|
1,9
|
| 9
|
11,2
|
3,0
|
93,0
|
11,33
|
-0,13
|
0,016
|
3,2
|
10,4
|
| 10
|
11,2
|
4,0
|
111,0
|
10,80
|
0,40
|
0,157
|
3,2
|
10,4
|
| 11
|
8,3
|
6,0
|
124,0
|
8,32
|
-0,02
|
0,000
|
0,3
|
0,1
|
| 12
|
5,6
|
6,0
|
81,0
|
5,63
|
-0,03
|
0,001
|
-2,4
|
5,6
|
| 13
|
5,6
|
6,0
|
71,0
|
5,00
|
0,60
|
0,361
|
-2,4
|
5,6
|
| 14
|
6,4
|
6,0
|
88,0
|
6,06
|
0,34
|
0,113
|
-1,6
|
2,5
|
| 15
|
5,3
|
7,0
|
112,0
|
5,92
|
-0,62
|
0,379
|
-2,7
|
7,1
|
| 16
|
4,0
|
7,0
|
88,0
|
4,41
|
-0,41
|
0,171
|
-4,0
|
15,8
|
Сумма
|
127,5
|
2,985
|
125,9
|
Остаточная дисперсия
S2
= ∑ (yi
-  i
)2
/ (n – m – 1) = 2,985 / (16 – 2 – 1) = 0,230 i
)2
/ (n – m – 1) = 2,985 / (16 – 2 – 1) = 0,230
Ковариационная матрица:
S2
(XT
X)-1
= 0,230 *  = = 
Стандартные ошибки коэффициентов равны квадратным корням из диагональных элементов ковариационной матрицы:
S0
=  = 0,787 = 0,787
S1
=  = 0,096 = 0,096
S2
=  = 0,005 = 0,005
Проверим значимость параметров регрессии.
Табличное значение
t1 – α/2, n – 3
= 1,77
t0
= |a0
| / S0
= 10,455 / 0,787 = 13,3 > 1,77
t1
= |a1
| / S1
= 1,650 / 0,096 = 17,1 > 1,77
t2
= |a2
| / S2
= 0,063 / 0,005 = 12,4 > 1,77
Все параметры значимы.
Коэффициент детерминации
 = 1 – 2,985 / 125,9 = 0,976 = 1 – 2,985 / 125,9 = 0,976
Табличное значение критерия Фишера
Fт
= 3,8
Расчетное значение
Fф
=  = =  = 267,7 > 3,8 = 267,7 > 3,8
Уравнение значимо.
Точечный прогноз:
 (xp
) = 10,455 – 1,650 * 3 + 0,063 * 165 = 15,83 тыс. у.е. (xp
) = 10,455 – 1,650 * 3 + 0,063 * 165 = 15,83 тыс. у.е.
Интервальный прогноз
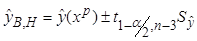
Квантиль распределения Стьюдента (по таблице)
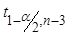 = t0,975; 13
= 2,16 = t0,975; 13
= 2,16
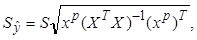
где S =  = =  = 0,479 = 0,479
xp
(XT
X)-1
(xp
)T
=    = =   = 0,633 = 0,633
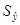 = 0,479 * = 0,479 *  = 0,381 = 0,381
 В,Н
= 15,83 ± 2,16 * 0,381 = 15,83 ± 0,68 В,Н
= 15,83 ± 2,16 * 0,381 = 15,83 ± 0,68
 Н
= 15,15 Н
= 15,15
 В
= 16,51 В
= 16,51
3. Экономическая интерпретация. Между возрастом автомобиля и его ценой существует тесная отрицательная связь (коэффициент корреляции –0,833): при увеличении возраста на 1 год (при фиксированной мощности двигателя) цена падает в среднем на 1,650 тыс. усл. ед.
Между мощностью двигателя и ценой автомобиля существует менее тесная положительная связь (коэффициент корреляции 0,665): при увеличении мощности на 1 л.с. (при фиксированном возрасте автомобиля) цена увеличивается в среднем на 0,063 тыс. усл. ед.
С вероятностью 0,95 можно утверждать, что цена автомобиля при возрасте 3 года и мощности двигателя 165 л.с. будет находиться в пределах от 15,15 до 16,51 тыс. усл. ед.
Задача 3
1. Для регрессионной модели
 и и
с помощью критерия Дарбина-Уотсона проверить наличие или отсутствие автокорреляции на уровне значимости 0,05.
2. Для регрессионной модели

проверить наличие или отсутствие мультиколлинеарности, используя:
а) парный коэффициент корреляции;
б) критерий «хи-квадрат» χ2
на уровне значимости 0,05.
Расчетная таблица:
| №
|
et
|
et-1
|
et
- et-1
|
(et
- et-1
)2
|
(et
)2
|
| 2
|
-0,85
|
0,42
|
-1,27
|
1,62
|
0,72
|
| 3
|
0,18
|
-0,85
|
1,03
|
1,05
|
0,03
|
| 4
|
-0,49
|
0,18
|
-0,67
|
0,45
|
0,24
|
| 5
|
0,73
|
-0,49
|
1,22
|
1,50
|
0,54
|
| 6
|
0,03
|
0,73
|
-0,70
|
0,49
|
0,00
|
| 7
|
0,09
|
0,03
|
0,06
|
0,00
|
0,01
|
| 8
|
-0,26
|
0,09
|
-0,35
|
0,12
|
0,07
|
| 9
|
-0,13
|
-0,26
|
0,13
|
0,02
|
0,02
|
| 10
|
0,40
|
-0,13
|
0,52
|
0,27
|
0,16
|
| 11
|
-0,02
|
0,40
|
-0,41
|
0,17
|
0,00
|
| 12
|
-0,03
|
-0,02
|
-0,01
|
0,00
|
0,00
|
| 13
|
0,60
|
-0,03
|
0,63
|
0,39
|
0,36
|
| 14
|
0,34
|
0,60
|
-0,26
|
0,07
|
0,11
|
| 15
|
-0,62
|
0,34
|
-0,95
|
0,91
|
0,38
|
| 16
|
-0,41
|
-0,62
|
0,20
|
0,04
|
0,17
|
| Сумма
|
7,11
|
2,81
|
Статистика Дарбина-Уотсона
 = 7,11 / 2,81 = 2,53 = 7,11 / 2,81 = 2,53
Табличные значения при n = 16, m = 2
dl
= 0,98; du
= 1,54
Так как 4 – du
< в < 4 – dl
, вопрос о наличии автокорреляции остается открытым (область неопределенности критерия).
Найдем коэффициент парной корреляции между объясняющими переменными.
r12
= 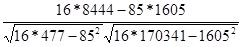 = -0,169 = -0,169
Проверим значимость коэффициента корреляции.
 = =  = 0,643 < 1,761 = 0,643 < 1,761
Коэффициент незначим, т.е. мультиколлинеарность не имеет места.
Определитель матрицы коэффициентов парной корреляции:
Det (r) =  = 1 – 0,1692
= 0,971 = 1 – 0,1692
= 0,971
Табличное значение статистики для df = 1 и α
= 0,05 равно
χ2
1;0,05
= 3,84.
Фактическое значение статистики
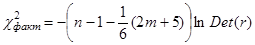 = - (16 – 1 – (2 * 2 + 5) / 6) ln 0,971 = 0,39 < 3,84 = - (16 – 1 – (2 * 2 + 5) / 6) ln 0,971 = 0,39 < 3,84
Мультиколлинеарность не имеет места, т.е. линейной зависимости между объясняющими переменными (возрастом автомобиля и мощностью двигателя) не существует. Это свидетельствует о надежности оценок параметров модели.
|