| 1. Графы
Задание 1.1
1. Охарактеризовать граф.
2. Выписать матрицу смежности графа.
3. Вычислить степени вершин.

Решение:
Данный граф является неографом, так как его ребра не ориентированные и не имеют начало и конец.
Ст. V1
=3
Ст. V2
=3
Ст. V3
=3
Ст. V4
=3
Ст. V5
=2
Ст. V6
=2
Матрица смежности графа
| Х1
|
Х2
|
Х3
|
Х4
|
Х5
|
Х6
|
Х7
|
Х8
|
| V1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
| V2
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
| V3
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
| V4
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
| V5
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
| V6
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
Задание 1.2
1. По матрице инцидентности нарисовать граф.
2. Охарактеризовать граф.
3. Назвать специальные вершины графа.
4. Вычислить полустепени вершин.
5. Выписать цикл, цепь, простой цикл, простую цепь.

Решение:
Данный граф называется орграфом, так как его ребра ориентированы и имеют начало и конец.
V4 и V6 – висячие вершины;
V5 – изолированная вершина.
Полустепень захода: V2 = 1; V3 = 3; V4 = 1; V6 = 1.
Полустепень исхода: V1 = 3; V2 = 1; V3 = 2.
Цепь:
Х1  Х2 Х2  Х6 Х6  Х3 Х3
Х5  Х6 Х6  Х3 Х3
Простая цепь:
Х1  Х2 Х2  Х3 Х3
Х5  Х3 Х3
Цикл: ????
V3  V3 V3
Простой цикл: ????
V3  V3 V3
Задание 1.3
1. Нагрузить граф задания 1.1. согласно матрице длин дуг и нарисовать.
2. По алгоритму окрашивания найти кратчайший путь между вершинами
V
1 и
V
6.
3. Построить покрывающее дерево с корнем в вершине
V
1.
| Х1
|
Х2
|
Х3
|
Х4
|
Х5
|
Х6
|
| V1
|

|
4
|
6
|
3
|

|

|
| V2
|
4
|

|
3
|
2
|

|

|
| V3
|
6
|
3
|

|

|

|
2
|
| V4
|
3
|
2
|

|

|
3
|

|
| V5
|

|

|

|
3
|

|
2
|
| V6
|

|

|
2
|

|
0
|

|
Решение:

Окрасила вершину V1. d(V1) = 0, d(x) =  для любого x для любого x  V1 и x = V1. V1 и x = V1.
1. в (V2) = 4
d (V3) = 6
d (V4) = 3 – наименьшее; закрашиваю вершину V4 и дугу (V1, V4) или (V4, V2)
y = V4
2. в (V2) = 4 – наименьшее; закрашиваю вершину V2 и дугу (V1, V2)
d (V3) = 6
d (V5) = min (6; 3+3) = 6
d (V6) = 
y = V2
3. в (V3) = 6 – наименьшее; закрашиваю вершину V3 и дугу (V2, V3)
d (V5) = 6
d (V6) = 
y = V3
4. в (V5) = 6 – наименьшее; закрашиваю вершину V5 и дугу (V4, V5)
d (V6) = min (8; 6+2) = 8
y = V5
5. в (V6) = 8 – закрашиваю вершину V6 и дугу (V5, V6)
Кратчайший путь
V1  V3 V3  V6. V6.
Покрывающее дерево:

2. Сетевое планирование
Задание 2.1
1. Для задачи планирования поставки товаров оптовым покупателям построить сетевой график, привязанный к оси времени, согласно структурно-временной таблицы. Задание конкретного варианта расположено в одной из пяти правых колонок таблицы.
| Содержание работ
|
Работа
|
Длитель-ность, ti
|
| Коэффициент, сi
|
Обозначение, аi
|
Опорная, аj
|
| отбор товара
|
0,1
|
a1
|
-
|
2
|
| подготовка к отправке
|
0,2
|
a2
|
a1
|
3
|
| выписка накладных
|
0,3
|
a3
|
a2
|
1
|
| определение объема отгрузки
|
0,4
|
a4
|
a3
|
1
|
| проверка цен
|
0,5
|
a5
|
a3
|
1
|
| оформления счета
|
0,6
|
a6
|
a5
|
1
|
| заказ автомашин для перевозки товара
|
0,7
|
a7
|
a4
а6
|
3
|
| отправка счета покупателю
|
0,8
|
a8
|
a4
а6
|
1
|
| проверка товара по счету
|
0,9
|
a9
|
a7
|
2
|
| оплата счета
|
1
|
a10
|
a8
|
12
|
| погрузка товара и проверка кол-ва
|
1,1
|
a11
|
a9
а10
|
2
|
| перевозка товара
|
1,2
|
a12
|
a11
|
4
|
| выгрузка и сверка с документами
|
1,3
|
a13
|
a12
|
4
|
2. Вычислить временные параметры сетевой модели.
3. Построить критический путь, вычислить критическое время, нанести критический путь на сетевой график.
Решение:

tij
– время выполнения работ;
Tp
– ранний срок наступления события;
K – номер вершины, при движении из которой было получено значение Tp
;
Tп
– поздний срок наступления события;
Rij
– полный резерв времени;
rij
– свободный резерв времени.

- критический путь.
Резервы нашла по формуле:
Rij
=  - Ti
- tij - Ti
- tij
rij
= 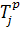 - - 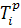 - tij - tij
На критическом пути резервов времени нет.
3. Система массового обслуживания (СМО)
Задание 3.1
Решить задачу для СМО с отказами:
В вычислительный центр с
m
ЭВМ поступают заказы на вычислительные работы. Если работают все
m
ЭВМ, то вновь поступающий заказ не принимается. Пусть среднее время работы с одним заказом составляет
 часов. Интенсивность потока заявок равна λ (1/ч). Найти вероятность отказа Ротк
и
m
3
– среднее число занятых ЭВМ. часов. Интенсивность потока заявок равна λ (1/ч). Найти вероятность отказа Ротк
и
m
3
– среднее число занятых ЭВМ.
Решение:
Интенсивность потока обслуживаний  = =  = =  = 0,33. Интенсивность нагрузки ЭВМ по формуле = 0,33. Интенсивность нагрузки ЭВМ по формуле
р =  ; р = ; р =  = 0,75. = 0,75.
Предельные вероятности состояний:
р0
= (1 + р + 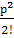 + … + + … +  + … + + … + 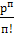 )-1
; р0
= (1 + 0,75 + 0,752
/ 2! + 0,753
/ 3!)-1
= 0,476 (нет ни одной заявки); )-1
; р0
= (1 + 0,75 + 0,752
/ 2! + 0,753
/ 3!)-1
= 0,476 (нет ни одной заявки);
рк
= рк
/ k! * р0
; р3
= (0,753
/ 3!) * 0,476 = 0,033 (заняты три ЭВМ).
Вероятность отказа (когда заняты три ЭВМ), таким образом, Ротк
= р3
= 0,033.
Относительная пропускная способность центра: Q = 1 - Ротк
; Q = 1 – 0,033 = 0,967, т. е. в среднем из каждых 100 заявок вычислительный центр обслуживает 96,7 заявок.
Абсолютная пропускная способность центра А = λ Q; А = 0,25 * 0,967 = 0,242, т. е. в один час в среднем обслуживается 0,242 заявки.
Среднее число занятых ЭВМ:  = А / = А /  ; ;  = 0,242 / 0,033 = 0,725, т. е. каждая из трех ЭВМ будет занята обслуживанием заявок в среднем лишь на 72,5 / 3 = 24,2%. = 0,242 / 0,033 = 0,725, т. е. каждая из трех ЭВМ будет занята обслуживанием заявок в среднем лишь на 72,5 / 3 = 24,2%.
Задание 3.2
Решить задачу для СМО с ограниченной длиной очереди:
На автозаправочной станции установлены
m
колонок для выдачи бензина. Около станции находится площадка на
L
машин для их ожидания в очереди. На станцию прибывает в среднем λ машин в минуту. Среднее время заправки одной машины
 мин. Требуется определить вероятность отказа Ротк
и среднюю длину очереди Мож
. мин. Требуется определить вероятность отказа Ротк
и среднюю длину очереди Мож
.
| m
|
3
|
| L
|
3
|
| λ
|
2
|
| 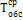
|
1
|
Решение:
 = 1 / = 1 /  = 1 мин. = 1 мин.
Нахожу:
р = λ /  = 2 / 1 = 2, р / m = 2 / 3, тогда = 2 / 1 = 2, р / m = 2 / 3, тогда
р0
= [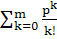 + +  * *  ]-1
= [1 + 2 + 22
/ 2! + 23
/ 3! + 24
/ 3*3! * ]-1
= [1 + 2 + 22
/ 2! + 23
/ 3! + 24
/ 3*3! *  ]-1 ]-1
 0.122 0.122
Ротк
= Pm
+
L
=  * p0
= (p/m)L
* (pm
/m!)*p0
= (2/3)3
* (23
/3!) * 0.122 = 0.048; * p0
= (p/m)L
* (pm
/m!)*p0
= (2/3)3
* (23
/3!) * 0.122 = 0.048;
Мож
=   i
= (0.122*23
/3!) * [2/3 + 2(2/3)2
+ 3*(2/3)3
] = 0.35 i
= (0.122*23
/3!) * [2/3 + 2(2/3)2
+ 3*(2/3)3
] = 0.35
Таким образом, Ротк
= 0,048, Мож
= 0,35 машины.
4. Игры
Задание 4.1
1. Решить игру в чистых стратегиях.
2. Выписать седловые точки.
3. Вычислить цену игры.
| В1
|
В2
|
В3
|
В4
|
| А1
|
1
|
4
|
1
|
2
|
| А2
|
0
|
5
|
0
|
3
|
| А3
|
1
|
3
|
1
|
3
|
Решение:

Седловые точки: (А1,В1); (А3,В1); (А1,В3); (А3,В3). V (цена игры) = 1.
Задание 4.2
1. Решить игру.
Указание: использовать принцип доминирования.
| В1
|
В2
|
В3
|
В4
|
В5
|
| А1
|
-2
|
1
|
3
|
0
|
1
|
| А2
|
-3
|
-4
|
2
|
-1
|
-4
|
| А3
|
1
|
-5
|
6
|
3
|
-5
|
| А4
|
-2
|
1
|
3
|
0
|
1
|
Решение:

Задание 4.3
1. Решить игру 2 х
n
графическим методом.
| В1
|
В2
|
В3
|
В4
|
| А1
|
-1
|
1
|
-1
|
2
|
| А2
|
0
|
-1
|
2
|
-2
|
Решение:
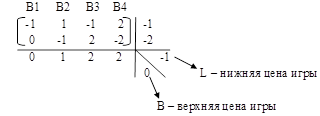
B – верхняя цена игры
А = (0,4;0,6)
 = 1. = 1.
5. Список литературы
1. Н. Ш. Кремер, Б. А. Путко, И. М. Тришин, М. Н. Фридман. Исследование операций в экономике: Учебн. Пособие для вузов/ Под ред. проф. Н. Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997.
2. Е. В. Бережная, В. И. Бережной. Математические методы моделирования экономических систем: Учеб. пособие. – М.: Финансы и статистика, 2001.
3. Лабскер Л. Г., Бабешко Л. О. Игровые методы в управлении экономикой и бизнесом: Учеб. пособие. – М.: Дело, 2001. – 464 с.
4. Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб. пособие. - М.: Дело, 2000. – 440 с.
5. Шапкин А.С., Мазаев Н.П. Математические методы и модели исследования операций: Учебник. – М.: Издательско-торговая корпорация "Дашков и К", 2004.
|