| КУРСОВАЯ РАБОТА (ПРОЕКТ)
по дисциплине:
«Принятие решения в условиях неопределённости»
ИСХОДНЫЕ ДАННЫЕ:
Выбор медицинской страховой компании
Фокус: выбор страховой компании.
Альтернативы: А, Б, В, Г.
Критерии: простота оформления, известность страховой компании, качество обслуживания, своевременность выплат, уровень страховых взносов, уровень страховки, степень охвата заболеваний.
1. ОПИСАНИЕ ПРОБЛЕМЫ
Необходимо сделать выбор медицинской страховой компании А (А1), Б (А2),
В (А3), Г (А4). Т.е. имеются четыре возможные альтернативы принятия решений.
Основными критериями при выборе медицинской страховой компании являются: простота оформления, известность страховой компании, качество обслуживания, своевременность выплат, уровень страховых взносов, уровень страховки, степень охвата заболеваний.
По отношению друг к другу данные критерии являются нейтральными, т.к. поиск решения по одному критерию никак не отражается на поиске решения по другому.
2. ПОСТРОЕНИЕ ИЕРАРХИЧЕСКОЙ СТРУКТУРЫ
|  
|
Выбор страховой компании
|
|     
|
| Простота оформления
|
Известность страховой компании
|
Качество обслуживания
|
Своевременность выплат
|
Уровень страховых взносов
|
Уровень страховки
|
Степень охвата заболеваний
|
|       
|
|    
|
| А
|
Б
|
В
|
Г
|
3. ПОСТРОЕНИЕ МАТРИЦ ПАРНЫХ СРАВНЕНИЙ АЛЬТЕРНАТИВ
Критерий: простота оформления
| А1
|
А2
|
А3
|
А4
|
| А1
|
1
|
2/1
|
4/1
|
8/1
|
| А2
|
1/2
|
1
|
3/1
|
6/1
|
| А3
|
1/4
|
1/3
|
1
|
4/1
|
| А4
|
1/8
|
1/6
|
1/4
|
1
|
Критерий: известность страховой компании
| А1
|
А2
|
А3
|
А4
|
| А1
|
1
|
1/2
|
1/4
|
1/5
|
| А2
|
2/1
|
1
|
1/3
|
1/4
|
| А3
|
4/1
|
3/1
|
1
|
1/2
|
| А4
|
5/1
|
4/1
|
2/1
|
1
|
Критерий: качество обслуживания
| А1
|
А2
|
А3
|
А4
|
| А1
|
1
|
3/1
|
4/1
|
5/1
|
| А2
|
1/3
|
1
|
3/1
|
3/1
|
| А3
|
1/4
|
1/3
|
1
|
2/1
|
| А4
|
1/5
|
1/3
|
1/2
|
1
|
Критерий: своевременность выплат
| А1
|
А2
|
А3
|
А4
|
| А1
|
1
|
7/1
|
2/1
|
3/1
|
| А2
|
1/7
|
1
|
1/6
|
7/1
|
| А3
|
1/2
|
6/1
|
1
|
2/1
|
| А4
|
1/3
|
1/7
|
1/2
|
1
|
Критерий: уровень страховых взносов
| А1
|
А2
|
А3
|
А4
|
| А1
|
1
|
1/3
|
1/5
|
0,17
|
| А2
|
3/1
|
1
|
1/2
|
1/4
|
| А3
|
5/1
|
2/1
|
1
|
1/2
|
| А4
|
6/1
|
4/1
|
2/1
|
1
|
Критерий: уровень страховки
| А1
|
А2
|
А3
|
А4
|
| А1
|
1
|
6/1
|
3/1
|
2/1
|
| А2
|
1/6
|
1
|
1/3
|
1/5
|
| А3
|
1/3
|
3/1
|
1
|
1/2
|
| А4
|
1/2
|
5/1
|
2/1
|
1
|
Критерий: степень охвата заболеваний
| А1
|
А2
|
А3
|
А4
|
| А1
|
1
|
1/2
|
1/4
|
1/5
|
| А2
|
2/1
|
1
|
1/3
|
1/4
|
| А3
|
4/1
|
3/1
|
1
|
1/2
|
| А4
|
5/1
|
4/1
|
2/1
|
1
|
4. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ МАТРИЦ ПАРНЫХ СРАВНЕНИЙ
Осуществляется по формуле:
V*(i,k) = (wi/w1*wi/w2*wi/w3*…*wi/w4)1/4
,
i - строка, k - матрица сравнений
V*(1,1) = (1×2×4×8)1/4
= 2,8284
V*(2,1) = 1,7321
V*(3,1) = 0,7598
V*(4,1) = 0,2686
V*(1,2) = 0,3976
V*(2,2) = 0,6389
V*(3,2) = 1,5651
V*(4,2) = 2,5149
V*(1,3) = 2,7832
V*(2,3) = 1,3161
V*(3,3) = 0,6389
V*(4,3) = 0,4273
V*(1,4) = 2,5457
V*(2,4) = 0,6389
V*(3,4) = 1,5651
V*(4,4) = 0,3899
V*(1,5) = 0,3247
V*(2,5) = 0,7825
V*(3,5) = 1,4953
V*(4,5) = 2,6321
V*(1,6) = 2,4495
V*(2,6) = 0,3263
V*(3,6) = 0,8388
V*(4,6) = 1,4953
V*(1,7) = 0,3976
V*(2,7) = 0,6389
V*(3,7) = 1,5651
V*(4,7) = 2,5149
5. НОРМАЛИЗАЦИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ МАТРИЦЫ
Осуществляется по формуле:
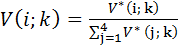
V(1,1) = 2,8284 / (2,8284+1,7321+0,7598+0,2686)1/4
= 0,5061
V(2,1) = 0,3099
V(3,1) = 0,1360
V(4,1) = 0,0481
V(1,2) = 0,0777
V(2,2) = 0,1249
V(3,2) = 0,3059
V(4,2) = 0,4915
V(1,3) = 0,5388
V(2,3) = 0,2548
V(3,3) = 0,1237
V(4,3) = 0,0827
V(1,4) = 0,4953
V(2,4) = 0,1243
V(3,4) = 0,3045
V(4,4) = 0,0759
V(1,5) = 0,0620
V(2,5) = 0,1495
V(3,5) = 0,2857
V(4,5) = 0,5028
V(1,6) = 0,4794
V(2,6) = 0,0639
V(3,6) = 0,1641
V(4,6) = 0,2926
V(1,7) = 0,0777
V(2,7) = 0,1249
V(3,7) = 0,3059
V(4,7) = 0,4915
6. ОПРЕДЕЛЕНИЕ СОГЛАСОВАНОСТИ МАТРИЦ
 Индекс согласованности определяется по формуле: С = (𝜆max
– N)/N – 1). Индекс согласованности определяется по формуле: С = (𝜆max
– N)/N – 1).
Параметр 𝜆max
вычисляется как: 𝜆max
𝜆max
1 = 4,0684 C1 = 0,0228
𝜆max
2 = 4,0486 C2 = 0,0162
𝜆max
3 = 4,1112 C3 = 0,0371
𝜆max
4 = 4,8372 C4 = 0,2791
𝜆max
5 = 4,0473 C5 = 0,0158
𝜆max
6 = 4,0389 C6 = 0,0130
𝜆max
7 = 4,0486 C7 = 0,0162
Используя значение ИСР, из таблицы для N=7, (1,32) получим:
Для А1 = 0,0228/1,32*100% = %<20%
Для А2 = 2,5348 %<20%
Для А3 = 1,8005 %<20%
Для А4 = 4,1178 %<20%
Для А5 = 31,0059 %<20%
Для А6 = 1,7517 %<20%
Для А7 = 1,4399 %<20%
Для А8 = 1,8005 %<20%
Расчёты для всех матриц <20%, что говорит о согласованности матриц.
7. АНАЛИЗ МАТРИЦЫ ПАРНЫХ СРАВНЕНИЙ КРИТЕРИЕВ
Будет страховой случай
| Простота оформления
|
Известность страховой компании
|
Качество обслуживания
|
Своевременность выплат
|
Уровень страховых взносов
|
Уровень страховки
|
Степень охвата заболеваний
|
| Простота оформления
|
1
|
1/2
|
1/3
|
1/5
|
2/1
|
3/1
|
1/4
|
| Известность страховой компании
|
2/1
|
1
|
1/2
|
1/4
|
3/1
|
4/1
|
1/3
|
| Качество обслуживания
|
3/1
|
2/1
|
1
|
1/3
|
4/1
|
6/1
|
1/2
|
| Своевременность выплат
|
5/1
|
4/1
|
3/1
|
1
|
6/1
|
7/1
|
2/1
|
| Уровень страховых взносов
|
1/2
|
1/3
|
1/4
|
1/6
|
1
|
2/1
|
1/5
|
| Уровень страховки
|
1/3
|
1/3
|
1/6
|
1/7
|
1/2
|
1
|
1/6
|
| Степень охвата заболеваний
|
4/1
|
3/1
|
2/1
|
1/2
|
5/1
|
6/1
|
1
|
Далее вычисляем собственные значения С*(i/L) (по принципу V*(i,k)):
С*(1/L) = 0,6518
С*(2/L) = 1,0000
С*(3/L) = 1,5746
С*(4/L) =3,3800
С*(5/L) = 0,4313
С*(6/L) = 0,3003
С*(7/L) = 2,3184
Нормализованные собственные значения (С(i/L)) равны (по принципу V(i,k)):
С(1/L) = 0,0675
С(2/L) = 0,1036
С(3/L) = 0,1631
С(4/L) =0,3500
С(5/L) = 0,0447
С(6/L) = 0,0311
С(7/L) = 0,2401
Не будет страхового случая
| Простота оформления
|
Известность страховой компании
|
Качество обслуживания
|
Своевременность выплат
|
Уровень страховых взносов
|
Уровень страховки
|
Степень охвата заболеваний
|
| Простота оформления
|
1
|
3/1
|
2/1
|
4/1
|
1/2
|
6/1
|
5/1
|
| Известность страховой компании
|
1/3
|
1
|
1/2
|
2/1
|
1/4
|
4/1
|
3/1
|
| Качество обслуживания
|
1/2
|
2/1
|
1
|
3/1
|
1/3
|
5/1
|
4/1
|
| Своевремен-ность выплат
|
1/4
|
1/2
|
1/3
|
1
|
1/5
|
3/1
|
2/1
|
| Уровень страховых взносов
|
2/1
|
4/1
|
3/1
|
5/1
|
1
|
7/1
|
6/1
|
| Уровень страховки
|
1/6
|
1/4
|
1/5
|
1/3
|
1/7
|
1
|
1/2
|
| Степень охвата заболеваний
|
1/5
|
1/3
|
1/4
|
1/2
|
1/6
|
2/1
|
1
|
Далее вычисляем собственные значения С*(i/L) (по принципу V*(i,k)):
С*(1/L) = 2,318
С*(2/L) = 1,000
С*(3/L) = 1,534
С*(4/L) = 0,652
С*(5/L) = 3,380
С*(6/L) = 0,296
С*(7/L) = 0,431
Нормализованные собственные значения (С(i/L)) равны (по принципу V(i,k)):
С(1/L) = 0,241
С(2/L) = 0,104
С(3/L) = 0,160
С(4/L) =0,068
С(5/L) = 0,352
С(6/L) = 0,031
С(7/L) = 0,045
8. ВЫЧИСЛЕНИЯ ВЕСА КАЖДОЙ АЛЬТЕРНАТИВЫ
Веса альтернатив если есть страховой случай
W(Ai
/L) = V(i,1)* С(1/L)+ V(i,2)* С(2/L)+ V(i,3)* С(3/L), i = 1,2,3…
W(A1
/L) = 0,340
W(A2
/L) = 0,158
W(A3
/L) = 0,259
W(A4
/L) = 0,244
При условии того, что будет страховой случай наилучшим вариантом при выборе страховой компании является «Медицинская страховая компания А».
Далее по убыванию: В (А3), Г (А4), Б (А2).
Веса альтернатив при условии отсутствия страхового случая
W(A1
/L) = 0,290
W(A2
/L) = 0,197
W(A3
/L) = 0,224
W(A4
/L) = 0,289
При условии отсутствия страхового случая наилучшим вариантом при выборе страховой компании является «Медицинская страховая компания А».
Далее по убыванию: Г (А4), В (А3), Б (А2).
9. ПРИНЯТИЕ ОПТИМАЛЬНОГО РЕШЕНИЯ С УЧЕТОМ ВЕРОЯТНОСТЕЙ ПРИРОДНЫХ УСЛОВИЙ.
| А1
|
0,340
|
0,290
|
0,29
|
29,08
|
| А2
|
0,158
|
0,197
|
0,20
|
19,62
|
| А3
|
0,259
|
0,224
|
0,22
|
22,49
|
| А4
|
0,244
|
0,289
|
0,29
|
28,81
|
| 0,020
|
0,980
|
1,00
|
W(A1
/L) = 0,340
W(A2
/L) = 0,158
W(A3
/L) = 0,259
W(A4
/L) = 0,244
С учётом вероятностей страхового случая преимущество имеет «Медицинская страховая компания А».
Далее по убыванию: Г (А4), В (А3), Б (А2).
|