| Министерство образования Республики Беларусь
Учреждение образования
"Гомельский государственный университет им. Ф. Скорины"
Математический факультет
Кафедра МПМ
Изучение тригонометрического материала в школьном курсе математики
Реферат
Исполнитель:
Студентка группы М-42 Головачева А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент Лебедева М.Т.
Гомель 2007
Содержание
Введение
1. Методика введения понятий синуса, косинуса и тангенса на геометрическом материале. Основные тригонометрические тождества
2. Методика введения определений тригонометрических функций углов от 0° до 180°
3. Методика изучения тригонометрических функций в курсе алгебры
4. Тождественные преобразования тригонометрических выражений. Тригонометрические уравнения и неравенства и методика обучения решению
Заключение
Литература
Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного треугольника; 2) затем введенные понятия обобщаются для углов от 00
до 1800
; 3) тригонометрические функции определяются для произвольных угловых величин и действительных чисел.
Первые два этапа реализуются в курсе планиметрии. Геометрический характер определений тригонометрических функций объясняет тот факт, что они составляют единственный вид функций, который начинают изучать не в курсе алгебры, а в курсе геометрии. Для геометрии важен "общефункциональный взгляд" на тригонометрические функции, а их прикладная сторона (решение прямоугольных треугольников, применение некоторых тригонометрических тождеств, теорем cos и sin, решение произвольных треугольников). Поэтому в курсе планиметрии нет термина "тригонометрические функции".
Знакомство с тригонометрическим материалом начинается в курсе геометрии при знакомстве с прямоугольным треугольником. Понятия 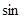 , , 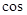 и и 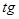 острых углов треугольника вводится для углов от острых углов треугольника вводится для углов от 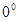 до до 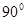 , как отношение сторон этого треугольника. Предварительно учащиеся должны усвоить названия сторон прямоугольного треугольника: катеты (стороны прямого угла) и гипотенуза (сторона противолежащая прямому углу). Для этого необходимо предложить учащимся прямоугольные треугольники, разнообразные по расположению вершин прямого угла и предложить назвать стороны треугольника. , как отношение сторон этого треугольника. Предварительно учащиеся должны усвоить названия сторон прямоугольного треугольника: катеты (стороны прямого угла) и гипотенуза (сторона противолежащая прямому углу). Для этого необходимо предложить учащимся прямоугольные треугольники, разнообразные по расположению вершин прямого угла и предложить назвать стороны треугольника.

Назовите катеты в  ABC, ABC,  APN. Назовите гипотенузы в APN. Назовите гипотенузы в  LKM и LKM и  EFA. Будут ли гипотенузами следующие отрезки: AB, KL, AP, AN, EF, FA в указанных треугольниках и почему? EFA. Будут ли гипотенузами следующие отрезки: AB, KL, AP, AN, EF, FA в указанных треугольниках и почему?
Следующие выражения "прилежащий" и "противолежащий" отрабатываются на следующем этапе. Для этого необходимо по указанным треугольникам предложить учащимся назвать прилежащие и противолежащие острым углам катеты. Назвать отрезки: KL, PN, EA и попросить учащихся назвать те углы, против которых лежат эти катеты или, которым они прилегают.
Первым вводится понятие 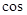 угла и доказывается теорема: " Косинус угла зависит от градусной меры угла и не зависит от расположения и размеров треугольника". Это определение уже " работает" при доказательстве теоремы Пифагора. угла и доказывается теорема: " Косинус угла зависит от градусной меры угла и не зависит от расположения и размеров треугольника". Это определение уже " работает" при доказательстве теоремы Пифагора.
С остальными понятиями учащиеся знакомятся в пункте " Соотношения между сторонами и углами в прямоугольном треугольнике". sin 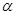 , tg , tg 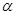

Формируется свойство: синус и тангенс угла так же, как и косинус, зависят от величины угла.
Для синуса это доказывается так:
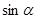 = =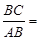 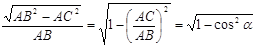 , ,
так как косинус зависит только от величины угла, то и синус зависит только от величины угла.
Из определений 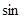 , , 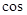 и и 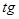 получаем следующие правила: получаем следующие правила:
- Катет, противолежащий углу 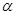 , равен произведению гипотенузы на синус , равен произведению гипотенузы на синус 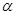 ; ;
- Катет, прилежащий к углу 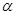 , равен произведению гипотенузы на косинус , равен произведению гипотенузы на косинус 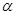 ; ;
- Катет, противолежащий углу 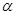 , равен произведению второго катета на тангенс , равен произведению второго катета на тангенс 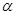 . .
По этим правилам можно находить неизвестные элементы в прямоугольном треугольнике.
Перечисленные правила могут быть выведены учащимися самостоятельно. Для этого предлагаются вопросы: В прямоугольном треугольнике MNP, LN=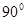 , LM= , LM=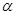 , гипотенуза MP=m. Найти длины катетов этого треугольника. ( Задача решается по определению). , гипотенуза MP=m. Найти длины катетов этого треугольника. ( Задача решается по определению).
Раньше по программе тригонометрические функции и соотношения между углами и сторонами в прямоугольном треугольнике изучались в курсе 8 класса.
После введения понятий 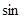 , , 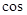 и и 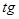 рассматривались решения основных задач, связанных с отысканием длин сторон и величин углов в прямоугольном треугольнике. рассматривались решения основных задач, связанных с отысканием длин сторон и величин углов в прямоугольном треугольнике.
Задача №1. Дано: a, b. Требуется найти  A, A,  B, c. B, c.
Задача №2. Дано: a, c. Требуется найти  A, A,  B, b. B, b.
Задача №3. Дано: a,  A. Требуется найти A. Требуется найти  A, b, c. A, b, c.
Задача №4. Дано: a,  B. Требуется найти B. Требуется найти  A, b, c. A, b, c.
Задача №5. Дано: a,  A. Требуется найти A. Требуется найти  B, a, b. B, a, b.
По действующей программе эти задачи в курсе 8 класса (бывший 7 класс) заменены такой: В прямоугольном треугольнике даны: гипотенуза c и острый угол 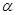 . Найдите катеты, их проекции на гипотенузу и высоту, опущенную на гипотенузу. . Найдите катеты, их проекции на гипотенузу и высоту, опущенную на гипотенузу.
Вводятся основные тригонометрические тождества:
 , ,  , ,  , , 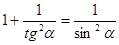 . .
В частности, основное тригонометрическое тождество выводится из формулировки теоремы Пифагора:
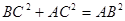 , ,  . .
Учащиеся знакомятся с некоторыми свойствами функций острого угла: 1) при возрастании острого угла 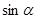 и и 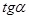 возрастают, а возрастают, а 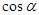 - убывает; 2) для любого острого угла - убывает; 2) для любого острого угла  : : 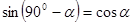 , , 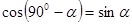 ; которые формулируются как теоремы. Их доказательство связывается с соотношениями острых углов в прямоугольном треугольнике: ; которые формулируются как теоремы. Их доказательство связывается с соотношениями острых углов в прямоугольном треугольнике:

 , ,  , тогда , тогда 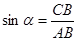 , , 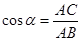 . .
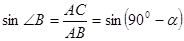 , ,
тогда из равенства правых частей получаем:
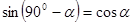 . .
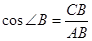 , тогда , тогда 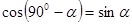 . .
Вывод свойства возрастания и убывания выглядит так:

Пусть  и и 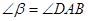 - острые углы, - острые углы, 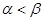 и и 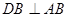 , и она пересекает стороны углов , и она пересекает стороны углов и и 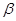 в точках в точках 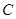 и и  соответственно. соответственно.
Так как 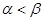 , то точка , то точка 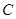 лежит между точками лежит между точками  и и  , тогда , тогда 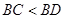 . А значит, по свойству наклонных, . А значит, по свойству наклонных, 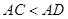 (через сравнение их проекций). Так как (через сравнение их проекций). Так как  , , 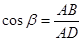 , то косинус убывает. А так как , то косинус убывает. А так как  , то синус возрастает. , то синус возрастает.
Расширение области определения тригонометрических функций от  до до  происходит в теме: "Декартовы координаты на плоскости". происходит в теме: "Декартовы координаты на плоскости".

Рассмотрим окружность с центром в начале координат произвольного радиуса R. Откладываем в полуплоскость  угол угол 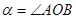 . Пусть точка . Пусть точка  имеет координаты имеет координаты  и и  . .   , ,  , то из треугольника , то из треугольника 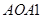 : : 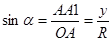 , ,  . .
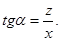 Определяются значения Определяются значения  и и 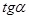 этими формулами для любого угла α (для этими формулами для любого угла α (для 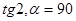 0
-исключается). 0
-исключается).

Можно найти значения этих функций для углов 900
, 00
, 1800
. Доказывается, что для любого угла α , 00
<α<1800
, 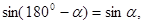 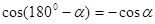 . .
  повернем подвижный радиус на угол 1800
-α= повернем подвижный радиус на угол 1800
-α=
  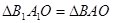 по гипотенузе и острому углу: => OB1
=OB; A1
B1
=AB => x = -x1
,y = y1
=> по гипотенузе и острому углу: => OB1
=OB; A1
B1
=AB => x = -x1
,y = y1
=>
    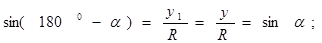 
Итак, в школьном курсе геометрии понятие тригонометрической функции вводится геометрическими средствами ввиду их большей доступности.
Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного треугольника; 2) затем введенные понятия обобщаются для углов от 00
до 1800
; 3) тригонометрические функции определяются для произвольных угловых величин и действительных чисел.
Первые два этапа реализуются в курсе планиметрии. Геометрический характер определений тригонометрических функций объясняет тот факт, что они составляют единственный вид функций, который начинают изучать не в курсе алгебры, а в курсе геометрии. Для геометрии важен "общефункциональный взгляд" на тригонометрические функции, а их прикладная сторона (решение прямоугольных треугольников, применение некоторых тригонометрических тождеств, теорем cos и sin, решение произвольных треугольников). Поэтому в курсе планиметрии нет термина "тригонометрические функции".
Конкретизировать, например, понятие cos острого угла прямоугольного треугольника, можно по следующей методической схеме:
1) построить на миллиметровой бумаге прямоугольный треугольник ABC;
2) обозначить величину острого угла А буквой α;
3) измерить (по клеткам) прилежащий катет АС и гипотенузу АВ;
4) вычислить отношение 
5) записать значение cos α (делается следующая запись cos α ≈ в которой для α не указывается его конкретное значение);
6) измерить транспортиром угол α, найти его величину и записать значение косинуса этого угла данного прямоугольного треугольника.
Определенные трудности в изучение элементов тригонометрии (по Пифагору) порождает теорема: "Косинус угла α зависит только от градусной меры угла". Необходимость изучения данной теоремы можно разъяснить учащемуся так: Пусть требуется на основании определения найти cos 370
. Предположим, что это задание выполняют отдельно друг от друга несколько человек. Чтобы найти cos 370
, они построят прямоугольный треугольник (каждый свой) с углом в 370
, измерят прилежащий катет и гипотенузу, найдут отношение прилежащего катета к гипотенузе. Полученное число и будет являться cos 370
. Есть ли гарантия, что каждый ученик получит один и тот же ответ? Этот вопрос возникает по той причине, что каждый строит свой треугольник, получает свои значения длин прилежащего катета и гипотенузы. Так, может быть, и искомое отношение у каждого ученика будет какое-то свое? Понятно, что если бы значение cos 370
при переходе от одного прямоугольного треугольника к другому изменялось, то ценность такого понятия в математике была бы не велика. Изучаемая терема является ответом на поставленные вопросы. Она утверждает, что косинус острого угла зависит не от выбора прямоугольного треугольника, а только от меры угла.
При решении прямоугольных треугольников необходимо обратить внимание учащегося на тот факт, что с каждой из формул для cos, sin и tg α связывается еще две формулы:
 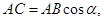 
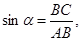  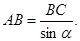
 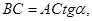 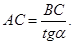
Определение cos, sin, tg углов от 00
до 1800
являются генетическими, т.к. в них указываются построения и вычисления, позволяющие найти значение тригонометрической функции.
В пособие говорится следующее (стр. 132, 1, 2 абзац), обратите внимание учащихся на следующее обстоятельство. Ранее для острых углов были установлены некоторые тригонометрические тождества. "Справедливы ли эти тождества для углов от 00
до 1800
. Справедливы ли прежние доказательства этих тождеств или необходимо привести новые?"
Сравним доказательства основного тригонометрического тождества: 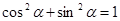 для острых углов и для углов от 00
до 1800
: для острых углов и для углов от 00
до 1800
:
| 00
<α<900
|
00
≤α≤1800
|
| 1 
|
1 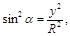 
|
| 2 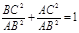
|
2 
|
| 3 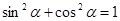
|
3 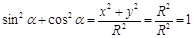
|
В курсе "Алгебра 9" обобщается определение cos, tg и sin α на случай произвольного угла α и вводится понятие ctg α. Возможность такого обобщения – во введении понятия угла поворота, положительного и отрицательного угла, понятия полного оборота. Доказывается, что тригонометрические функции, их значение, не зависит от длины радиуса.
Здесь же приведены с доказательствами основные тригонометрические формулы, формулы сложения и их следствия.
Традиционная методическая схема изучения тригонометрических функций:
· в начале определяются тригонометрические функции для острого угла прямоугольного треугольника;
· затем введенные понятия обобщаются для углов от 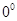 до до  ; ;
· тригонометрические функции определяются для произвольных угловых величин и действительных чисел.
В курсе алгебры и начала анализа осуществляется заключительный этап изучения, который включает:
a) Закрепление представлений учащихся о радианной мере угла; отработка навыков перехода от градусной меры к радианной и наоборот;
b) Формирование представлений об углах с градусной мерой, большей 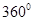 ; формирование представлений об углах с положительной и отрицательной градусными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа); ; формирование представлений об углах с положительной и отрицательной градусными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа);
c) Описание тригонометрических функций на языке радианной меры угла;
d) Утверждение функциональной точки зрения на  , , 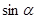 , и , и 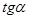 (трактовка (трактовка  , , 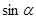 , и , и 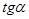 как функций действительного аргумента, установление области определения, области значений, построение графика функции, установление промежутков монотонности, знакопостоянства и т.д.); как функций действительного аргумента, установление области определения, области значений, построение графика функции, установление промежутков монотонности, знакопостоянства и т.д.);
e) Повторение известных и ознакомление с новыми тригонометрическими тождествами, ключом которых является тождество 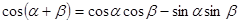 ; ;
f) Применение тригонометрических тождеств в тождественных преобразованиях и при решении задач по стереометрии.
В курсе "Алгебра 9" учащиеся знакомятся с функциональной точкой зрения. Выражения 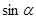 и и 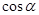 определимы при определимы при 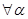 , т.к , т.к  угла поворота можно найти соответствующее значение дробей угла поворота можно найти соответствующее значение дробей 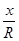 и и  . Выражение . Выражение 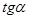 имеет смысл при имеет смысл при  , кроме углов поворота , кроме углов поворота 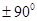 , , 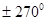 , …, т.к. имеет смысл дробь , …, т.к. имеет смысл дробь 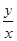 . .
Каждому допустимому значению 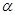 соответствует единственное значение соответствует единственное значение 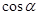 , , 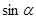 , , 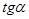 и и  . Поэтому . Поэтому  , , 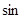 , , 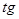 и и 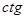 являются функциями угла являются функциями угла 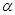 . Их называют тригонометрическими функциями. . Их называют тригонометрическими функциями.
Учащиеся знакомятся со следующими общефункциональными свойствами этих функций:
1. область значения  и и 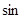 - - 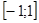 , для , для 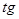 и и 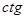 - множество всех действительных чисел - множество всех действительных чисел
2. промежутки знакопостоянства: 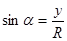 , то значит , то значит  зависит от знака зависит от знака 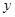 и т.д. и т.д.
3. 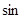 , , 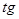 и и 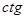 являются нечетными функциями, а являются нечетными функциями, а  является четной функцией является четной функцией
4. при изменении угла на целое число оборотов значение  , ,  , , 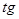 , , 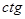 не изменится (под обратным понимаем поворот на не изменится (под обратным понимаем поворот на 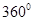 ). ).
Введение радианной меры угла основывается на том факте, что отношения длины окружности к её радиусу постоянно для данного центрального угла и не зависит от выбора концентрических окружностей. По этой причине меру центрального угла можно охарактеризовать действительным числом 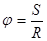 . Если . Если 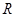 положить равным 1, то радианная мера центрального угла равна 1, т.е. положить равным 1, то радианная мера центрального угла равна 1, т.е.  . .
Тогда для каждого угла, заданного в градусах, достаточно вычислить соответствующую дугу единичной окружности. Длина такой дуги будет выражать меру данного угла в радианах.
Радианная мера угла позволяет любому действительному числу поставить в соответствие определенную градусную меру угла по формуле: 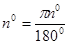 , где , где  . .
Переход от радианной меры угла к действительному числу осуществляется на основании того, что  . Учащимся следует показать изменение величин углов по координатным углам: . Учащимся следует показать изменение величин углов по координатным углам:
1 четверть:  , ,  ; ; 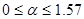
2 четверть:  , ,  ; ; 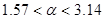 и т.д. и т.д.
Определение тригонометрической функции 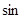 выглядит так: выглядит так:
Опр.
Окружность радиуса 1 с центром в начале координат называют единичной
окружностью. Пусть точка 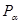 единичной окружности получена при повороте точки единичной окружности получена при повороте точки 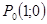 на угол в на угол в 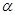 радиан. Ордината точки радиан. Ордината точки 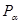 - это синус угла - это синус угла 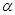 . Числовая . Числовая 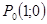 функция, заданная формулой функция, заданная формулой 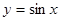 , называется синусом числа, каждому числу , называется синусом числа, каждому числу 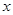 ставится в соответствие число ставится в соответствие число  . .
Устанавливаются области определения и значения функций, напоминаются свойства:
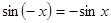 ; ;  . .

Делим единичную окружность и отрезок 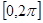 на 16 равных частей. на 16 равных частей.
Через точку 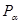 проводим прямую, параллельную проводим прямую, параллельную 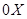 . Проводим прямую . Проводим прямую  до пересечения с построенной прямой. Получим одну из точек графика функции до пересечения с построенной прямой. Получим одну из точек графика функции 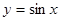 , называемого синусоидой. , называемого синусоидой.
Для построения графика синуса вне этого отрезка заметим, что 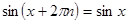 . Поэтому во всех точках вида . Поэтому во всех точках вида 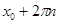 , где , где 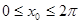 , значения синуса совпадают, и, следовательно, график синуса на всей прямой получается из построенного графика с помощью параллельных переносов его вдоль оси , значения синуса совпадают, и, следовательно, график синуса на всей прямой получается из построенного графика с помощью параллельных переносов его вдоль оси 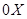 . .
Для построения графика косинуса следует вспомнить, что 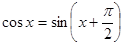 . Следовательно, значение косинуса в произвольной точке . Следовательно, значение косинуса в произвольной точке 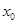 равно значению синуса в точке равно значению синуса в точке 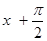 . Это значит, что график косинуса получается из графика синуса с помощью параллельного переноса на расстояние . Это значит, что график косинуса получается из графика синуса с помощью параллельного переноса на расстояние 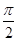 в отрицательном направлении оси в отрицательном направлении оси 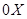 . Поэтому график функции . Поэтому график функции 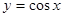 также является синусоидой. также является синусоидой.
Построение графика: проведем касательную 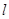 к единичной окружности в точке к единичной окружности в точке  . .

Пусть  произвольное число, для которого произвольное число, для которого  . Тогда точка . Тогда точка  не лежит на оси ординат, и, следовательно, прямая не лежит на оси ординат, и, следовательно, прямая 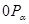 пересекает пересекает  в некоторой точке в некоторой точке  с абсциссой 1. Найдем ординату этой точки. Для этого заметим, что прямая с абсциссой 1. Найдем ординату этой точки. Для этого заметим, что прямая 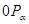 проходит через точки проходит через точки 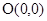 и и 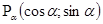 . Поэтому она имеет уравнение . Поэтому она имеет уравнение 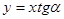 . .
Абсцисса точки 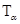 , лежащей на этой прямой, равна 1. Из уравнения прямой , лежащей на этой прямой, равна 1. Из уравнения прямой 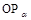 находим, что ордината точки находим, что ордината точки 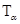 равна равна 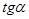 . Итак, ордината точки пересечения прямых . Итак, ордината точки пересечения прямых 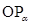 и и 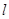 равна равна 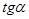 . Поэтому прямую . Поэтому прямую 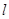 называют линией тангенсов. называют линией тангенсов.
  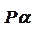 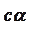 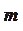  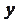 Нетрудно доказать, что абсцисса точки Нетрудно доказать, что абсцисса точки 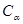 пересечения прямой пересечения прямой 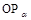 с касательной m к единичной окружности, проведённой через точку с касательной m к единичной окружности, проведённой через точку  , равна , равна  при при 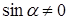 . .

Поэтому прямую m называют линией котангенсов.
Область значений
 - вся числовая прямая. Докажем это для функции - вся числовая прямая. Докажем это для функции 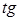 . Пусть . Пусть 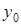 - произвольное действительное число. Рассмотрим точку - произвольное действительное число. Рассмотрим точку  . Как только что было показано, . Как только что было показано, 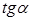 равен равен 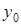 . Следовательно, функция . Следовательно, функция 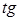 принимает любое действительное значение принимает любое действительное значение 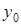 , ч.т.д. , ч.т.д.
Можно построить схему, позволяющую изобразить график тригонометрических функций:
1) Начертить единичную окружность, горизонтальный диаметр которой служит продолжением оси 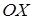 . Разделить её на равные части (например,16). . Разделить её на равные части (например,16).
2) Для функции  выбираем отрезок выбираем отрезок 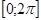 , для функции , для функции 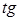 - -  и делим их на то же равное число частей. и делим их на то же равное число частей.
3) По окружности находим соответствующее число значений этих функций.
4) Точки пересечения горизонтальных линий, отвечающих значениям функций и вертикальных линий, отвечающих значениям аргумента, представляют собой точки графика.
Тригонометрический материал изучается в школьном курсе в несколько этапов.
1) Функции тригонометрических функций для углов от 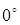 до до 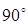
(прямоугольный треугольник, планиметрия);
2) Тригонометрические функции для углов от 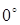 до до 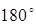 (тема: "Декартовы координаты на плоскости; геометрия"); (тема: "Декартовы координаты на плоскости; геометрия");
3) Тригонометрические функции для любого действительного числа.
Параллельно изучению теоретического материала учащиеся знакомятся с тригонометрическими формулами, объём которых будет постепенно рассширяться. Умение "выделить" эти формулы в дальнейшем поможет в преобразовании тригонометрических выражений.
К обязательным результатам обучения за курс геометрии в 7-9 классах относиться умение решать типичные задачи на вычисление значений геометрических величин (длин, углов, площадей) с привлечением свойств фигур, аппарата алгебры и тригонометрии.
Например:
1) В прямоугольном треугольнике найдите катеты, если его гипотенуза равна 5 см, а один из углов равен 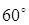 . .
2) В прямоугольном треугольнике катет равен 4 см, а прилежащий к нему угол равен 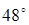 . Найдите другой катет и гипотенузу. . Найдите другой катет и гипотенузу.
3)   В треугольнике ABC: AB=3см, BC=6 см, В треугольнике ABC: AB=3см, BC=6 см, 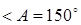 . Определите . Определите  . .
4) В треугольнике ABC известны стороны: AB=4 см; BC=5 см; AC=6 см.
 Найдите угол B. Найдите угол B.

Существуют различные доказательства формулы косинуса суммы двух аргументов.
 Одно из наиболее простых доказательств основано на применении системы координат и формулы расстояние между двумя точками. Воспроизвести доказательство по опорному конспекту: Одно из наиболее простых доказательств основано на применении системы координат и формулы расстояние между двумя точками. Воспроизвести доказательство по опорному конспекту:
1. 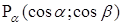 ; ;
2.  ; ;
3. 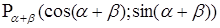 ; ;
4. 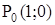 ; ;
5.  . .
6. 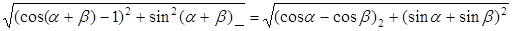 ; ;
 , ч.т.д. , ч.т.д.
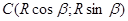 ; ; 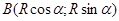 - -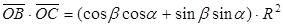 . .

 С другой стороны: С другой стороны:
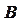 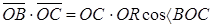 - -
 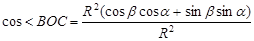 - - 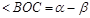 - -
 - теорема сложения. - теорема сложения.

и по доказанной формуле.
Для доказательства 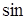 суммы и разности двух углов используются формула приведения, которые помогают преобразовать функции от аргументов вида: суммы и разности двух углов используются формула приведения, которые помогают преобразовать функции от аргументов вида:
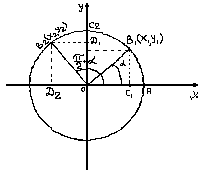
 , , 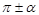 , , 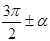 , ,  . .
Проведём радиус 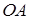 , длина которого равна , длина которого равна 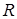 , на угол , на угол 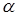 : и получили радиус : и получили радиус 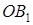 , где , где  и на угол и на угол 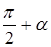 и получим радиус и получим радиус  , где , где 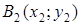 . .
 , , 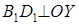 : : 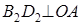 , , 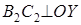 . .
 - прямоугольник. Повернём его на угол - прямоугольник. Повернём его на угол 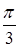 вокруг точки вокруг точки 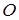 : :
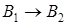 ; ; 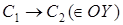 ; ; 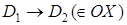 , т.е. , т.е.
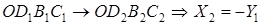 ; ;  , т.е: , т.е:
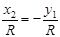 ; ; 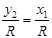 , по , по  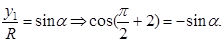
Аналогично:
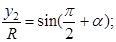 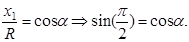
Тогда:
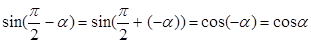
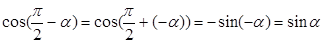

и т.д.

К функциям от углов 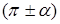 можно прийти и из геометрических соображений. можно прийти и из геометрических соображений.
Формулы приведения для  и и 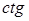 выводится из определения этих функций и ранее полученных формул приведения для синуса и косинуса. После этого полученные результаты сводятся в одну таблицу, с помощью которой можно сформулировать мнемоническое правило. Желательно учащимся предложить алгоритм применения формул приведения. Поясним его на примере: выводится из определения этих функций и ранее полученных формул приведения для синуса и косинуса. После этого полученные результаты сводятся в одну таблицу, с помощью которой можно сформулировать мнемоническое правило. Желательно учащимся предложить алгоритм применения формул приведения. Поясним его на примере:
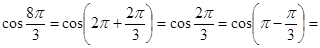 {определяем четность, в которой оканчивается угол {определяем четность, в которой оканчивается угол 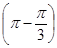 - II четверть; определяем знак данной функции в этой четверти – " - ". Изменяется ли название функции – нет, поэтому:} - II четверть; определяем знак данной функции в этой четверти – " - ". Изменяется ли название функции – нет, поэтому:}  = - cos = - cos 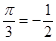 . .
Вернёмся к выводу формулы синуса суммы и разности двух углов.
 , ,
а затем применяется уже известная формула.
Формулы двойного угла выводятся из формулы синуса и косинуса суммы и разности двух углов, положив 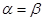 . .
Сумму и разность тригонометрических функций можно преобразовать в произведение, используя следующий пример:
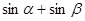 ={ ={  , , 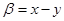 }= }=
= , ,
но:
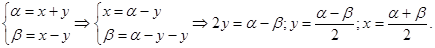
Таким образом:
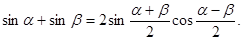
Замечание: при ознакомлении учащихся с формулами следует добиваться от них проговаривания словесных формулировок доказываемых формул.
Например: сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
В курсе алгебры 9 класса изучается тема: "Элементы тригонометрии" (30 часов):
1) радианное измерение углов, sin, cos, tg произвольного угла, их нахождение с помощью калькулятора;
2) основные тригонометрические тождества:

Их применение для вычисления значений sin, cos, tg;
3) формулы приведения; sin, cos суммы и разности двух углов; sin и cos двойного угла;
4) тождественные преобразования тригонометрических выражений; основная цель – сформировать умения выполнять тождественные преобразования несложных тригонометрических выражений с использованием формул, указанных в программе:
Рассмотрим некоторые примеры преобразований тригонометрических выражений:
Задача №1.
Доказать тождество:

Преобразуем левую часть и получим, применив формулы приведения:
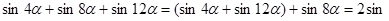 8 8 cos4 cos4 +sin8 +sin8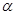 =2sin8 =2sin8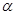 cos4 cos4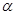 +2sin4 +2sin4 cos4 cos4 =2cos4 =2cos4 (sin8 (sin8 +sin4 +sin4 )=4cos4 )=4cos4 sin6 sin6 cos2 cos2 , и т.д. , и т.д.
Задачи №2.
Упростить выражение
а) 
Можно применить формулы понижения степени:
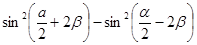 = =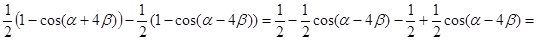
 {воспользуемся преобразованием разности косинусов в произведение по формуле: {воспользуемся преобразованием разности косинусов в произведение по формуле: 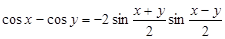 } = } =

б)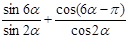
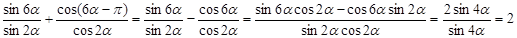
Задача №3
Преобразовать в произведение:
а) cos5 +sin8 +sin8 +cos9 +cos9 +cos12 +cos12 =(cos5 =(cos5 +cos12 +cos12 )+(cos8 )+(cos8 +cos9 +cos9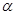 )= )=
=2cos17/2 cos7/2 cos7/2 +2cos17/2 +2cos17/2 cos cos /2=2cos17/2 /2=2cos17/2 (cos7/2 (cos7/2 +cos +cos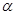 /2)= /2)=
=4cos17/2 cos2 cos2 cos3/2 cos3/2 =4cos3/2 =4cos3/2 cos2 cos2 cos17/2 cos17/2
б) 3+4cos4 +cos8 +cos8 =3(1+cos4 =3(1+cos4 )+(cos4 )+(cos4 +cos8 +cos8 )=6cos2
2 )=6cos2
2 + +
+2cos6 cos2 cos2 =2 cos2 =2 cos2 (3cos2 (3cos2 +cos6 +cos6 )=2cos2 )=2cos2 ((cos2 ((cos2 +|cos6 +|cos6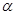 )+ )+
+2cos2 )=2cos2 )=2cos2 (2cos4 (2cos4 cos2 cos2 +2cos2 +2cos2 )=4cos2
2 )=4cos2
2 (cos4 (cos4 +cos2 +cos2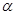 )= )=
=4cos2
2 cos2
2 cos2
2 =8cos4
2 =8cos4
2
Задача №4
Найти sin4
 +cos4 +cos4
 , если известно, что: , если известно, что:
sin -cos -cos =1/2 =1/2
sin4
 +cos4 +cos4
 =(sin2 =(sin2
 +cos2 +cos2
 )2
-2sin2 )2
-2sin2
 cos2 cos2
 =1-2sin2 =1-2sin2
 cos2 cos2
 = =
=1-1/2sin2
2 ={sin4 ={sin4 -cos -cos =1/2 =1/2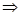 (sin (sin -cos -cos )2
= )2
=
=1-2sin cos cos =1/4 =1/4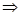 sin2 sin2 =3/4}= =3/4}=
Задача №5
Вычислить:

sin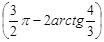 =-cos(2arctg4/3)={обозначим arctg4/3 через y, тогда получим cos2y, который нужно преобразовать в тангенс половинного угла. Применим формулу =-cos(2arctg4/3)={обозначим arctg4/3 через y, тогда получим cos2y, который нужно преобразовать в тангенс половинного угла. Применим формулу 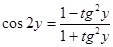 и получим}= и получим}= 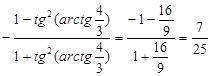
Определенные трудности в изучение элементов тригонометрии (по Пифагору) порождает теорема: "Косинус угла α зависит только от градусной меры угла". Необходимость изучения данной теоремы можно разъяснить учащемуся так: Пусть требуется на основании определения найти cos 370
. Предположим, что это задание выполняют отдельно друг от друга несколько человек. Чтобы найти cos 370
, они построят прямоугольный треугольник (каждый свой) с углом в 370
, измерят прилежащий катет и гипотенузу, найдут отношение прилежащего катета к гипотенузе. Полученное число и будет являться cos 370
. Есть ли гарантия, что каждый ученик получит один и тот же ответ? Этот вопрос возникает по той причине, что каждый строит свой треугольник, получает свои значения длин прилежащего катета и гипотенузы. Так, может быть, и искомое отношение у каждого ученика будет какое-то свое? Понятно, что если бы значение cos 370
при переходе от одного прямоугольного треугольника к другому изменялось, то ценность такого понятия в математике была бы не велика. Изучаемая терема является ответом на поставленные вопросы. Она утверждает, что косинус острого угла зависит не от выбора прямоугольного треугольника, а только от меры угла.
1. К.О. Ананченко "Общая методика преподавания математики в школе", Мн., "Унiверсiтэцкае",1997г.
2.Н.М.Рогановский "Методика преподавания в средней школе", Мн., "Высшая школа", 1990г.
3.Г.Фройденталь "Математика как педагогическая задача",М., "Просвещение", 1998г.
4.Н.Н. "Математическая лаборатория", М., "Просвещение", 1997г.
5.Ю.М.Колягин "Методика преподавания математики в средней школе", М., "Просвещение", 1999г.
6.А.А.Столяр "Логические проблемы преподавания математики", Мн., "Высшая школа", 2000г.
|