Дипломная работа: Методика использования дидактических игр на уроках математики в начальной школе

УО “Белорусский государственный педагогический университет

имени М. Танка”

Дипломная работа:

Методика использования дидактических игр на уроках математики в начальной школе

Содержание

Введение.......................................................................................................... 2

Глава 1 Проблема игровой деятельности в педагогической и методической литературе...................................................................................................... 5

1.1. Понятие об игре и её видах......................................................... 5

1.2. Особенности использования игр в 1 классе............................... 8

Глава 2 Методика использования дидактических игр на уроках математики в 1 классе при изучении темы “Нумерация чисел

в пределах сотни”....................................................................................... 12

2.1. Исследование отношения детей и учителей к дидактическим

играм на уроках математики.................................................. 12

2.2. Особенности использования дидактических игр при

объяснении нового материала................................................ 15

2.3. Способы использования дидактических игр при закреплении

материала................................................................................. 24

2.4. Особенности применения дидактических игр при обобщении

знаний учащихся...................................................................... 34

Заключение................................................................................................... 40

Литература................................................................................................... 42

Приложение.................................................................................................. 43

Введение

Проблемы методов обучения сегодня приобретают всё большее значение. Этой проблеме посвящено множество исследований в педагогике и психологии. И это закономерно, т.к. учение – ведущий вид деятельности школьников, в процессе которого решаются главные задачи, поставленные перед школой: подготовить подрастающее поколение к жизни, к активному участию в научно-техническом и социальном процессе. Общеизвестно, что эффективное обучение находится в прямой зависимости от уровня активности учеников в этом процессе. В настоящее время дидакты пытаются найти наиболее эффективные методы обучения для активизации и развития у учащихся познавательного интереса к содержанию обучения. В связи с этим много вопросов связано с использованием на уроках занимательного материала. И среди них особое значение уделяется дидактическим играм на уроках математики.

Данная проблема широко рассматривается в работе В.А.Сухомлинского “О воспитании”. В этой книге он знакомит нас со своими мыслями о воспитании детей в семье и школе, в том числе автор пишет об использовании игры: “…Игра – это огромное светлое окно, через которое в духовный мир ребёнка вливается живительный поток представлений, понятий об окружающем мире. Игра – это искра, зажигающая огонёк пытливости и любознательности.”[1] Продолжая работу Сухомлинского, в своей работе “Психология игры” Эльконин Д.Б. пишет, что игра влияет на развитие психических процессов: “Значение игры не ограничивается тем, что у ребёнка возникают новые по своему содержанию мотивы деятельности и связанные с ними задачи. В игре возникает новая психологическая форма мотивов”.[2] Продолжая работу Эльконина, Амонашвили Ш.А. в своей книге “В школу - с шести лет” описывает опыт обучения шестилетних детей в школах, а также рассматривает проблему использования игры на уроках: “Дидактическая игра, если не делать из неё самоцель, может выполнить свою исключительную роль усиления сложного процесса учения, ускорения развития,”[3] что и определяет актуальность нашей работы.

Цель курсовой работы – определить наиболее эффективные методы использования дидактических игр на уроках математики в 1 классе. В связи с этим были поставлены следующие задачи:

- дать понятие о дидактической игре;

- раскрыть особенности использования дидактических игр;

- исследовать отношение детей и учителей к дидактическим играм на уроках математики;

- изучить особенности использования дидактических игр при объяснении нового материала на уроках математики в 1 классе при изучении темы “Нумерация чисел в пределах сотни”;

- выявить эффективные способы использования дидактических игр при обобщении материала.

Объектом исследования является процесс обучения математике младших школьников.

Предметом исследования выступает совокупность методов, способов и средств обучения, которые использует учитель на уроках математики в начальной школе.

При написании курсовой работы были использованы следующие методы психолого-педагогического исследования:

1) теоретический анализ психологической и педагогической литературы по проблеме (изучены работы В.А.Сухомлинского, Д.Б.Эльконина, Ш.А.Амонашвили);

2) анкетирование с целью выявления отношения детей к играм на уроках математики (анкеты прилагаются);

3) анкетирование с целью выявления отношения учителей к играм на уроках (анкеты прилагаются);

4) анализ и обобщение передового опыта по проблеме (изучен опыт работы учителей Е.А.Бочек, В.И.Поповой);

5) анализ собственного опыта работы в 1 “А” классе школы №121 г.Минска.

Глава 1 Проблема игровой деятельности
в педагогической и методической литературе

1.1. Понятие об игре и её видах

Игра имеет особое важное значение в жизни детей дошкольного и младшего школьного возраста. С.А.Шацкий, высоко оценивая значение игры, писал: “Игра, эта жизненная лаборатория детства, дающая тот аромат, ту атмосферу молодой жизни, без которой эта пора её была бы бесполезна для человечества. В игре, этой специальной обработке жизненного материала, есть самое здоровое ядро разумной школы детства.”

У философов своя точка зрения на игру, они утверждают: “Игра – это особая форма детской жизни, выработанная или созданная обществом для управления развитием детей, в этом смысле она есть особое педагогическое творение”. Щедровицкий Г.П. пишет, что игра есть:

1.особое отношение ребёнка к окружающему миру;

2.особая деятельность ребёнка, которая изменяется и развёртывается как его субъективная деятельность;

3.социально заданный и усвоенный ребёнком вид деятельности;

4.деятельность, в ходе которой происходит усвоение самого разнообразного содержания и развитие психики ребёнка;

5.социально-педагогическая форма организации всей детской жизни.[4]

Д.Б.Эльконин даёт такое определение игры: “Человеческая игра – это такая деятельность, в которой воссоздаются социальные отношения между людьми вне условий непосредственно утилитарной деятельности.”[5]

Также игра – одно из важнейших средств умственного и нравственного воспитания детей; это средство, снимающее неприятные или запретные для личности школьника переживания.

Игры подразделяются на творческие и игры с правилами. Творческие игры, в свою очередь включают: театральные, сюжетно-ролевые и строительные игры. Игры с правилами – это дидактические, подвижные, музыкальные игры и игры–забавы.

Какое же значение имеет игра? В процессе игры у детей вырабатывается привычка сосредотачиваться, мыслить самостоятельно, развивается внимание, стремление к знаниям. Увлёкшись, дети не замечают, что учатся: познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию. Даже самые пассивные из детей включаются в игру с огромным желанием, прилагают все усилия, чтобы не подвести товарищей по игре.

Из всего существующего многообразия различных видов игр именно дидактические игры самым тесным образом связаны с учебно-воспитательным процессом. Они используются в качестве одного из способов обучения различным предметам в начальной школе, в том числе особое место данные игры занимают на уроках математики.

Дидактическая игра (игра обучающая) – это вид деятельности, занимаясь которой, дети учатся.[6] Дидактическая игра, как и каждая игра, представляет собой самостоятельный вид деятельности, которой занимаются дети: она может быть индивидуальной или коллективной. Данная игра является ценным средством воспитания действенной активности детей, она активизирует психические процессы, вызывает у учащихся живой интерес к процессу познания. В ней охотно дети преодолевают значительные трудности, тренируют свои силы, развивают способности и умения. Она помогает сделать любой учебный материал увлекательным, вызывает у учеников глубокое удовлетворение, создаёт радостное рабочее настроение, облегчает процесс усвоения знаний. В дидактических играх ребёнок наблюдает, сравнивает, сопоставляет, классифицирует предметы по тем или иным признакам, производит доступный ему анализ и синтез, делает обобщения.

Существенный признак дидактической игры – устойчивая структура, которая отличает её от всякой другой деятельности.[7] Структурные компоненты дидактической игры: игровой замысел, игровые действия и правила.

Игровой замысел выражен, как правило, в названии игры. Игровые действия способствуют познавательной активности учащихся, дают им возможности проявить свои способности, применить имеющиеся знания, умения и навыки для достижения целей игры. Правила помогают направлять игровой процесс. Они регулируют поведение детей и их взаимоотношения между собой. Дидактическая игра имеет определённый результат, который является финалом игры, придаёт игре законченность. Она выступает прежде всего в форме решения поставленной учебной задачи и даёт школьникам моральное и умственное удовлетворение. Для учителя результат игры всегда является показателем уровня достижений учащихся в освоении знаний или в их применении.

Все структурные элементы дидактической игры взаимосвязаны между собой и отсутствие любого из них разрушает игру.

1.2. Особенности использования игр в 1 классе.

Для младшего школьного возраста учение – новое и непривычное дело. Поэтому при знакомстве со школьной жизнью игра способствует снятию барьера между “внешним миром знания” и психикой ребёнка. Игровое действие позволяет осваивать то, что заранее вызывает у младшего школьника страх неизвестности, постоянно внушаемое уважение к премудростям школьной жизни, что мешает свободному освоению знаний.

Основным типом дидактических игр, используемых при начальных этапах, являются игры, формирующие устойчивый интерес к учению и снимающие напряжённость, которое возникает в период адаптации ребёнка к школьному режиму.

Психолого-педагогические особенности проведения дидактических игр.[8]

1. Во время игры учитель должен создавать в классе атмосферу доверия, уверенности учащихся в собственных силах и достижимости поставленных целей. Залогом этого является доброжелательность, тактичность учителя, поощрение и одобрение действий учащихся.

2. Любая игра, предлагаемая учителем, должна быть хорошо продумана и подготовлена. Нельзя для упрощения игры отказываться от наглядности, если она требуется.

3. Учитель должен быть очень внимательным к тому, насколько учащиеся подготовлены к игре, особенно к творческим играм, где учащимся представляется большая самостоятельность.

4. Следует обратить внимание на состав команд для игры. Они подбираются так, чтобы в каждой были участники разного уровня и при этом в каждой группе должен быть лидер.

В процессе игр учитель должен постепенно воспитывать ведущих из числа лидеров, а в простых играх предлагать роль ведущего поочерёдно разным учащимся.

Не следует приучать детей к тому, чтобы на каждом уроке они ждали новых игр или сказочных героев. Необходим последовательный переход от уроков, насыщенных игровыми ситуациями, к урокам, где игра является поощрением за работу на уроке или используется для активизации внимания: весёлые шутки-минутки, игры-путешествия в страну чисел или страну знаний.

Особенно широко используются игры на уроках при обучении детей шести-семилетнего возраста, поскольку ведущей деятельностью детей до поступления была игра, а с поступлением в школу происходит смена ведущей деятельности на учебную. Надо иметь в виду, что очень эффективными являются игровые формы обучения, различного рода дидактические игры. В этих условиях переход от одной ведущей деятельности к другой происходит безболезненно. Надо шире практиковать занимательные игровые формы обучения, которые вызывают большой интерес у детей (например, игру в магазин при обучении математике, обведение контуров рисунка при обучении письму, игру с куклами и мячами на уроках по развитию речи и т.д.[9] )

Даже слаборазвитые, робкие и застенчивые дети охотно включаются в подобные игры. При этом надо чётко представлять себе, какую именно дидактическую нагрузку несёт содержание той или иной игры, и постепенно совершенствовать эту дидактическую основу. В ситуации весёлой, увлекательной дидактической игры дети более успешно усваивают знания, чем в процессе учебных занятий.

Разумеется, обучение нельзя превращать в сплошную игру. И в дальнейшем ученики, когда станут старше, поймут, что учение не игра, а труд, и труд серьёзный и ответственный, хотя по-прежнему радостный и увлекательный.[10]

Младший школьник мыслит наглядно-образно, поэтому необходимо при применении дидактических игр использовать наглядность. Игра должна быть занимательной, интересной для детей, но ни в коем случае нельзя принудительно заставлять детей играть. Это не даст желаемого результата ни в развивающем, ни в образовательном плане.

В игре детям следует предоставлять большую самостоятельность, в то же время на них нельзя возлагать и большую ответственность. Важно, чтобы ребята сами следили за выполнением правил, чтобы каждый участник игры чувствовал ответственность перед коллективом.[11]

Дидактические игры кратковременны (10-20 мин.), и важно, чтобы всё это время не снижалась умственная активность играющих, не падал интерес к поставленной задаче. Особенно важно следить за этим в коллективных играх. Нельзя допустить. чтобы решением задачи был занят один ребёнок, а другие бездействовали. Обычно при таком проведении игры дети быстро утомляются от пассивного ожидания. Другая картина наблюдается, если все играющие включены в решение задачи.[12]

В игре проявляются особенности характера ребёнка, обнаруживается уровень его развития. Поэтому игра требует индивидуального подхода к детям. Учитель должен считаться с индивидуальными особенностями каждого ребёнка при выборе задания, постановке вопроса: одному дать задание надо легче, другому – труднее, одному стоит задать наводящий вопрос, а от другого потребовать вполне самостоятельного решения. Особого внимания требуют дети робкие, застенчивые: иногда такой ребёнок знает правильный ответ, но от робости не решается ответить, смущенно молчит. Учитель помогает ему преодолеть застенчивость, одобряет его, хвалит за малейшую удачу, старается чаще его вызывать, чтобы приучить выступать перед классом (коллективом).

Дидактические игры особенно необходимы в воспитании и обучении детей шестилетнего возраста. В них удаётся сконцентрировать внешне даже самых инертных детей. В начале дети проявляют интерес только к игре, а затем и к тому учебному материалу, без которого участие в игре невозможно. Как показывают наблюдения за детьми шестилетнего возраста, наибольших успехов достигают те учителя, которые отводят на игру третью часть урока. Недооценка или переоценка игры отрицательно сказывается на учебно-воспитательном процессе. При недостаточном использовании игры снижается активность учащихся на уроке, ослабляется интерес к обучению, при её чрезмерном использовании ученики с трудом переключаются на обучение в неигровых условиях.

Глава 2 Методика использования дидактических игр на уроках математики в 1 классе при изучении темы “Нумерация чисел в пределах сотни”

2.1. Исследование отношения детей и учителей к дидактическим играм на уроках математики

Одной из поставленных задач курсовой работы было выявление отношений учителей и учащихся к дидактической игре. В результате этого в школе №121 было проведено анкетирование учителей и учащихся. В анкетировании приняло участие 14 учителей. В процессе опроса были выявлены следующие данные:

Вопрос №1:

На вопрос №1: “Какое место занимает игра в развитии личности ребёнка”. 57% опрошенных учителей считает “самое главное”, 43% - “не самое главное”.

Вопрос №2: “Вы в своей педагогической практике много времени отводите дидактической игре в учебном процессе?” 57% учителей ответило “очень много”, а 43% - не очень много, но достаточно.

По мнению основной массы опрошенных учителей (10 чел. – 71,4%), главной трудностью в проведении дидактической игры является отсутствие в школе необходимых условий. И лишь 28,6% учителей не имеют трудностей в проведении дидактических игр. По этому вопросу можно составить следующую таблицу.

Вывод : учителя положительно относятся к дидактической игре и активно используют её в своей педагогической деятельности, несмотря на объективные трудности в проведении, и не считают игру пустой тратой времени.

Но для того, чтобы дидактическая игра прочно влилась в учебный процесс, необходимо обеспечить школу (особенно начальную), соответствующими техническими средствами обучения и пособиями для проведения такого рода игр.

В школе №121 также были проанкетированы учащиеся начальных классов. В опросе приняло участие 32 ученика из шести классов по произвольному выбору. В таблице указаны те ответы, которые выбрали ученики.

Из всего этого можно сделать вывод: учащимся начальной школы нравятся все уроки, положительно относятся к использованию игры на уроках. Если бы учащиеся были учителями, то более 50% использовали бы на своих уроках игры. И практически основная масса детей считает, что игра на уроках приносит большую пользу и с удовольствием в них участвуют.

Таким образом, необходимо в каждый урок включать игровые моменты, но не в качестве разрядки обстановки, а с целью активизации знаний детей, развития психических процессов.

2.2. Особенности использования дидактических игр при объяснении нового материала

Игра ценна только в том случае, когда она содействует лучшему пониманию математической сущности вопроса, уточнению и формированию математических знаний учащихся. Дидактические игры и игровые упражнения стимулируют общение между учениками и преподавателем, отдельными учениками, поскольку в процессе проведения этих игр взаимоотношения между детьми начинают носить более непринуждённый и эмоциональный характер.

Практика показывает, что занимательный материал применяется на разных этапах усвоения знаний: на этапах объяснения нового материала, его закрепления, повторения, контроля. Использование дидактических игр оправдано только тогда, когда они тесно связаны с темой урока, органически сочетаются с учебным материалом, соответствующим дидактическим целям урока.[13]

В практике начальной школы имеется опыт использования игр на этапе повторения и закрепления изученного материала и крайне редко применяются игры для получения новых знаний.

При объяснении нового материала необходимо использовать такие игры, которые содержат существенные признаки изучаемой темы. Также в ней должны быть заложены практические действия детей с группами предметов или рисунков.

При изучении раздела “Нумерация чисел первого десятка” используются прежде всего такие игры, с помощью которых дети осознают приёмы образования каждого последующего и предыдущего числа. На этом этапе можно применить игру “Составим поезд”:

Дидактическая цель: ознакомить детей с приёмом образования чисел путём прибавления единицы к предыдущему числу и вычитания единицы из последующего числа.

Содержание игры: учитель вызывает к доске поочерёдно учеников. Каждый из них выполняет роль вагона, называет свой номер. Например, первый вызванный ученик говорит: “Я первый вагон”. Второй ученик, выполняя роль второго вагона, цепляется к первому вагону (кладёт руку на плечо ученика, стоящего впереди). Называет свой порядковый номер, остальные составляют пример: “Один да один, получится два”. Затем цепляется третий вагон, и все дети по сигналу составляют пример на сложение: “Два да один – это три”. Потом вагоны (ученики) отцепляются по одному. а класс составляет примеры вида: “Три без одного – это два. Два без одного – это один”[14] .

На основе использования игры “Составим поезд” учащимся предлагают считать число вагонов слева направо и справа налево и подводят их к выводу: считать числа можно в одном направлении, но при этом важно не пропустить ни одного предмета и не сосчитать его дважды.

Также при знакомстве детей с приёмом образования чисел можно использовать игру “Живой уголок”.

Дидактическая цель: ознакомление детей с приёмом образования чисел при одновременном закреплении пространственной ориентации, понятий “больше”, “меньше”.

Средства обучения: изучение животных.

Содержание игры: учитель говорит: “В нашем живом уголке живут кролики: серый и белый, кролики грызут морковь. Сколько кроликов грызут морковь? (два, ответ фиксируется показом цифры 2). Назовите, какие кролики грызут морковь? (серый и белый). К ним прибежал ещё один кролик. Что изменилось? (кроликов стало больше) Сколько кроликов теперь едят морковь? (три, ответ фиксируется показом цифры 3) Перечисли их (один белый и ещё один белый, и ещё один серый, всего три). Каких кроликов больше, белых или серых? (белых) Почему их больше? (их два, а два это один и один). Почему 2>1? (два идёт при счёте после числа 1). Аналогично можно рассматривать образование последующих чисел.[15]

При изучении нумерации в пределах десяти необходимо довести до понимания детей, что последнее названное при счёте число обозначает общее количество всей группы предметов. С этой целью следует проводить игры “Лучший счётчик”, “Хлопки”. С помощью этих игр дети устанавливают соответствие между числом и цифрой.

“Лучший счётчик”

Содержание игры: учитель на магнитном моделеграфе по секторам соответственно размещает от 1 до 10 рисунков. Открывая каждый сектор поочерёдно, учитель предлагает детям сосчитать число рисунков и показать нужную цифру. Сосчитавший первый называется лучшим счётчиком. Затем учитель показывает цифры вразбивку, а ученики – соответствующее число рисунков в секторах круга. В итоге игры учитель открывает 2 сектора, предлагает сравнить число рисунков в них и определить, где предметов меньше и на сколько.

“Хлопки”

Содержание игры: учитель на магнитном моделеграфе размещает по секторам от 1 до 10 рисунков. Открывая по очереди сектор за сектором, предлагает сосчитать число рисунков и по его сигналу похлопать столько же раз, сколько открыто рисунков, и показать нужную цифру. (учитель задаёт ритм хлопков).

Изучая числа первого десятка, важно сравнивать каждое предыдущее число с последующим и наоборот. Для этого предназначены игры “Лучший счётчик”, “Число и цифру знаю я”.

Содержание игры: учитель на магнитном моделеграфе поочередно открывает сектор за сектором, дети считают число цифр в каждом из них и показывают учителю соответствующую карточку с цифрой, а затем сравнивают число цифр в двух соседних секторах магнитного моделеграфа.

Работа над составом числа начинается в разделе “Нумерация чисел первого десятка”. Состав чисел от одного до пяти дети в этот период должны знать на память, состав чисел 6-10 можно рассматривать на наглядной основе, на следующем этапе дети знакомятся с составом чисел на основе сложения по памяти. На третьем этапе дети воспроизводят состав чисел на основе выявленной закономерности: числа, стоящие на одинаковых местах (слева и справа) в числовом ряду, составляет в сумме последнее число в этом ряду.

В этот период большую помощь учащимся в изучении состава чисел окажет игра “Числа, бегущие навстречу друг другу”:

Дидактическая цель: знакомство с составом числа 10.

Содержание игры: учитель предлагает детям записать в тетрадь числа от 1 до 10 по порядку и дугами показать два числа, которые бегут навстречу друг другу, образуя в сумме число 10. Затем просит записать примеры на сложение с этими числами. Например:

0 1 2 3 4 5 6 7 8 9 10

0 + 10 = 10 10 + 0 = 10

1 + 9 = 10 9 + 1 =10

Учитель спрашивает: “Что интересного вы заметили при составлении примеров? Дети отвечают, что числа, стоящие на одинаковых местах справа и слева в числовом ряду, составляют в сумме число 10”.

При изучении нумерации чисел в пределах 20 можно выделить 4 этапа:

1. Образование чисел путём прибавления единицы к предыдущему числу и вычитание единицы из последующего числа. Игра “Составим поезд”.

2. Образование чисел из десятков и единиц. Здесь можно предложить игру “Математическая эстафета”.

3. Анализ состава чисел в пределах 20. Можно использовать игру “Узнай, сколько палочек в другой руке” (описание игры в п.3).

4. Письменная нумерация чисел в пределах 20. На этом этапе можно предложить игру “Стук-стук” (описание игры в п.3).

“Математическая эстафета”

Дидактическая цель: ознакомление с образованием чисел из десятка и единиц.

Средства обучения: 10 кругов и 10 треугольников из приложенных к учебнику математики для подготовительного класса.

Содержание игры: учитель делит класс на 3 команды по рядам и проводит игру-соревнование. Первый ученик из первой команды иллюстрирует число с помощью кругов и треугольников, второй из этой же команды называет цифрой обозначенное число, третий – его состав, четвёртый показывает число на карточках.

Аналогичные упражнения выполняют из второй и третьей команд. Победит та команда, которая не допустит ни одной ошибки или допустит меньшее их число.

При изучении нумерации чисел в пределах 100 задача состоит в том, чтобы научить считать и записывать числа.

Установлению связи между устной и письменной нумерацией поможет известная игра “Молчанка”.

Содержание игры: учитель иллюстрирует на абаке или карточках двузначные числа, а учащиеся обозначают их с помощью разрезных цифр и показывают их молча учителю или записывают в тетради.

Для глубокого осознания принципа поместного значения цифр используются иллюстративные (с помощью цифр) рассказы “Спор цифр” и “Как запутался Серёжа?”.

“Как запутался Серёжа?”

Серёжа научился писать числа в пределах сотни. Однажды вечером отец положил перед Серёжей на стол 4 палочки слева и один десяток связанных палочек справа и предложил мальчику написать, сколько палочек всего. Серёжа написал число 41. Правильно ли написал число Серёжа? Как он рассуждал?

“Спор цифр”.

Однажды цифры поспорили с нулём и стали его дразнить: Ты хотя тоже цифра, но ровнехонько ничего не значишь! Вот ученик возьмёт цифру 2 и поставит два кубика, а возьмёт тебя и ничего не поставит.

- Правда, правда, ни-че-го – сказала пятёрка.

- Ни-че-воч-ка, ни-че-воч-ка, - затараторили цифры.

- Глупые вы, ничего не понимаете, - сказал ноль, - Вот единица. Я встану рядом с тобой справа. Чем ты теперь стала? Отвечай!

Ноль встал справа рядом с единицей, и она стала … (десяткой).

- Вот я стану рядом с тобой справа, пятерка, что ты будешь обозначать? Отвечай! – Ноль встал справа рядом с пятёркой, и стала она … (пятью десятками, 50)

Ноль становится рядом справа с каждой цифрой и требовал ответить, чем она стала.

- Я увеличиваю каждую из вас, а вы меня ничевочкой называли. Неблагодарные! Подумайте хорошенько, и вы поймёте, что я для вас значу. Когда вас нет, я вас всегда заменяю. Можете ли вы написать ответ в таких примерах: 5–5=… , 7-7=…? А ну-ка, попробуйте! Никого из вас нельзя здесь поставить.

Задумались цифры и перестали дразнить ноль. Но цифрам всё же захотелось поспорить, и они затеяли спор между собой.

- Я больше всех значу, - заявила девятка, - я не какая-то единица.

Единица засмеялась, подскочила к девятке слева и закричала:

- Кто теперь больше, ты или я? Отвечай! (получилось 19)

- Я десяток, а ты только девять; десять ведь больше девяти. Что, молчишь?

Подбежала семёрка, прогнала единицу и сама стала слева. Получилось (79).

- Я семь десятков, 70, понимаешь?

Так все цифры становились рядом с девяткой и все оказывались больше неё. Удивилась девятка, смутилась…

Учитель спрашивает:

- Правильно ли спорят цифры? Какой вывод можно сделать?

- Девятка больше всех, когда цифры живут отдельно. Когда они становятся рядом друг с другом, дело меняется. Самое главное – это место цифр в числе. На первом месте справа пишутся единицы, на втором справа – десятки.

Цифры поняли и с тех пор перестали спорить, кто из них больше.

Примечание: на уроке инсценировку “Спор цифр” может прочитать учитель или ученик, а во внеклассной работе её можно и драматизировать: за автора читает учитель, один ученик становится нулём, девять детей изображают цифры. В этой игре дети усваивают зависимость значения цифры от занимаемого его места.

Приведённые примеры далеко не исчерпывают всего разнообразия игр. Учитель может придумывать свои игры, используя местный материал, учитывая индивидуально-психологические особенности своих детей.

При написании курсовой работы использовался материал, накопленный при работе в подготовительном классе “А” школы 121, на уроках математики в классе проводились различные дидактические игры. Например, на уроке по теме “Состав числа 5” проводилась дидактическая игра “Подарки Петрушки”:

Дидактическая цель: ознакомить с составом числа 5.

Средства обучения: иллюстрации Петрушки, Незнайки и Веселого Карандаша; воздушные шары, вырезанные из цветного картона.

Содержание игры: учитель сообщает, что на урок в гости пришёл Петрушка с воздушными шарами и с ним пришли его друзья. Незнайка и Весёлый Карандаш (на доску крепятся иллюстрации с изображением сказочных героев). Петрушка решил подарить шары Незнайке и Весёлому Карандашу. Как он может подарить их?

Дети перечисляют возможные варианты состава числа пять и иллюстрируют у доски и после записывают в тетрадь. В конце игры наиболее активные дети поощряются.

При изучении темы состав числа 10 была проведена игра

“Украсим ёлку игрушками”:

Дидактическая цель: знакомство с составом числа 10.

Средства обучения: рисунок ёлки; маленькие иллюстрации ёлочек для учащихся.

Содержание игры: учитель сообщает, что скоро Новый год. И все будут наряжать ёлку. И нам с вами тоже надо нарядить ёлку. Наша ёлка – математическая. На доску вывешивается плакат с ёлкой. На верхушке - звезда с числом 10. Но не все ветки украшены игрушками, надо повесить ещё недостающие шарики так, чтобы на каждом ярусе сумма чисел была равна 10. Дети выходят к доске и наряжают ёлку. Учитель должен поощрять слабых детей.

Данные дидактические игры помогли учащимся осмысленно усвоить состав числа. Дети чувствовали себя свободно, непринуждённо, с интересом участвовали в играх.

2.3. Способы использования дидактических игр при закреплении материала

На уроках закрепления нового материала важно применять игры на воспроизведение свойств, действий, вычислительных приёмов и т.д. В этом случае использование средств наглядности следует ограничить и направить внимание на проговаривание вслух правил, свойств, вычислительных приёмов. При закрепление материала форма проведения игры может быть разной: коллективной, групповой и индивидуальной. Целесообразно проводить игры в группах и в виде соревнования. Для проведения соревнования учитель в таблице на доске звёздочками отмечает дружную работу команд в течение урока. Если активность и интерес детей какой-либо команды ослабевает (например, из-за того, что команда набрала меньшее число очков, учитель должен спросить такого ученика из этой команды, который ответит правильно и заработает звезду. В конце урока учитель вместе с детьми подводя итоги соревнования, обращает внимание на дружную работу участников команд, что способствует формированию чувства коллективизма. Необходимо отнестись с большим тактом к детям, допустившим ошибки. Ошибки учащихся надо анализировать не в ходе игры, а в конце, чтобы не нарушать общего впечатления от игры.

Для закрепления устной нумерации в пределах 100 используется игра “Цепочка”, при проведении которой дети каждого ряда (команды) на основе иллюстративного материала образуют числа в пределах 100, соревнуясь друг с другом.

“Цепочка”

Содержание игры: учитель выставляет для каждого ряда (команды) на подставку доски карточки, изображающие числа вида:

Учащиеся каждого ряда (команда) считают единицы каждого разряда и по цепочке называют проиллюстрированные числа (сначала ученик первой, потом второй и третьей команды). Потом учитель ставит другие карточки, иллюстрирующие числа второго десятка и ученики по цепочке называют их. Игра продолжается аналогично.

Выигрывает команда, которая допустит меньше ошибок в образовании двузначных чисел. Для подведения итогов игры учитель отмечает в таблице звёздочками правильные ответы учащихся.

Для закрепления состава чисел можно предложить следующие игры: “Арифметический лабиринт”, “Угадай-ка!”, Эстафета”. Смысл этих игр заключается в том, что дети проговаривают все случаи состава числа 10 и выигрывает тот, кто назовёт наибольшее число комбинаций. Можно провести игру в виде соревнования по рядам. Также здесь можно предложить игру “Контролёры”.

Дидактическая цель: закрепление знания состава чисел первого десятка.

Содержание игры: учитель распределяет детей на две команды. Два контролёра у доски следят за правильностью ответов: один – первой команды, второй - другой команды. По сигналу учителя ученики первой команды делают несколько ритмических наклонов вправо, влево и считают про себя. По сигналу учителя они называют хором число наклонов первой команды до заданного числа и ведут счёт про себя (например 6 – прибавил 1, 7 – прибавил 2, 8 – прибавил 3). Затем они называют число выполненных наклонов. По числу наклонов, выполненных учениками 1 и 2 группы и называется состав числа. Учитель говорит: “Восемь – это…”, ученики продолжают: “Пять и четыре”. Контролёры показывают зелёные круги в правой руке, если согласны с ответом, красные – если нет. В случае ошибки упражнение повторяется. Потом учитель предлагает детям второй команды по сигналу сделать несколько приседаний, а ученики первой команды дополняют приседания до заданного числа. Называется состав числа. Аналогично анализируется состав чисел на основе хлопков.

Данная игра не только систематизирует знания учеников, но и несёт элементы физической разгрузки, т.к. использует физкультурные упражнения.

При закреплении состава десятичного состава двузначных чисел используются игры “Сколько палочек в другой руке?”, “Хлопки”.

“Сколько палочек в другой руке?”

Дидактическая цель: закрепление знания десятичного состава двузначного числа.

Средства обучения: набор отдельных палочек и пучков палочек.

Содержание игры: вызванный ученик берёт пучок палочек в одну руку, а отдельные палочки – в другую руку и показывает их классу. Дети угадывают их количество и показывают карточку с соответствующим числом.

Затем задание усложняется: надо угадать, сколько отдельных палочек в руке, если в другой – пучок, и составить пример на сложение. Например, ученик взял 15 палочек, положив пучок из 10 палочек в правую руку и 5 отдельных палочек в левую. Дети составляют пример на сложение 10+5=15.

“Хлопки”

Цель игры: закрепление знания десятичного состава двузначного числа.

Средства обучения: набор определённых палочек и пучков палочек.

Содержание игры: учитель вызывает двух детей к доске. Ученик, стоящий справа, обозначает единицы, а стоящий справа – десятки. Учитель называет двузначное число, правый ученик хлопками обозначает число единиц в этом числе, а левый – число десятков. Все остальные ученики выполняют роль контролёров. Они сигналят, если десятичный состав числа показан учениками неверно.

Как уже упоминалось в п.2 при изучении нумерации чисел в пределах 20 выделяют 4 этапа. Один из этапов – это письменная нумерация чисел в пределах 20. Здесь можно предложить игру “Стук-стук”.

Дидактическая цель: закрепление знаний по нумерации чисел в пределах 20.

Средства обучения: на доске изображена таблица с двумя разрядами:

Содержание игры: учитель молча стучит указкой один раз в разряде десятков и несколько раз в разряде единиц. Дети внимательно слушают и показывают учителю соответствующее число на карточке с цифрами.

Для закрепления навыков счёта можно предложить игру “Слушай и считай” :

Содержание игры: у каждого из учеников набор карточек с числами от 1 до 10. У учителя палочка, которой он ударяет по какому-либо предмету, издающему громкий звук, определённое число раз. Все учащиеся должны немедленно поднять и показать карточку с числом, соответствующим количеству ударов.

Можно условиться, что играющие, услышав удары, должны поднять карточку с числом, недостающим, например, до десяти (ударов было три, поднять карточку с числом 7). Затем устанавливается другое правило: показать надо не число, соответствующее числу ударов, а два соседних числа – меньшее и большее. Можно предложить и другой вариант игры: учитель сначала ударит палочкой по одному предмету 8 раз, а по другому – 3 раза. Это значит, что учащиеся должны от восьми отнять три и показать карточку с числом 5. Игра требует тишины и внимания, поэтому можно предложить ребятам, прислушиваясь к числу ударов, закрывать глаза.

В теме “Нумерация чисел первой сотни” для усвоения порядка следования чисел при счёте, порядковых и количественных отношений между смежными числами можно использовать игры “Считай дальше с любого числа”, “Назови соседей числа”,“Кто быстрей сосчитает? ”.

“Считай дальше с любого числа”

Эта игра поможет избавиться от ошибки, когда ученик называет число с переходом через круглый десяток, например, 67, 68, 69, 70 (а не шестьдесят десять).

“Назови соседей числа”

Эта игра даёт возможность каждое число первой сотни рассматривать не изолированно, а в связи с предыдущим и последующим числом.

Средства обучения: мяч или два мяча – большой и маленький (или разного цвета).

Содержание игры: учитель бросает мяч то одному, то другому участнику игры, а те, возвращая мяч, отвечают на вопрос учителя. Бросая мяч, учитель называет какое-либо число, например двадцать один, играющий должен назвать смежные числа – 20 и 22 (обязательно сначала меньшее, потом большее).

Возможен и другой, более сложный вариант игры. Возвращая мяч, играющий должен сначала отнять от названного учителем числа единицу, потом прибавить к нему полученную разность. Например, учитель назвал число 11, а играющий должен назвать числа

10 (11-1=10) и 21 (11+10=21).

Эту игру можно провести и с двумя мячами: большим и маленьким (или разного цвета). Когда учитель бросает большой мяч, то отвечающий должен, к примеру, прибавить 9 и вернуть мяч обратно, а когда маленький – то отнять 3. Здесь дети не только считают, но и развивают внимание, чтобы не перепутать действия.

“Кто быстрей сосчитает?”

Игра развивает зоркость, внимание.

Содержание игры: на доске вывешиваются два одинаковых плаката, на которых записаны в произвольном порядке числа. Например, от 61 до 90 (от 11 до 30 и т.п.). Например, требуется назвать и указать на таблице по порядку все числа от 61 до 90. Можно соревноваться и двумя командами, по одному человеку от каждой. Затем победители соревнуются между собой и определяется лучший счётчик.

Примерный вид плаката:

Также на этапе закрепления можно предложить следующие игры:

“Загадка”

Дидактическая цель: закрепить нумерацию чисел в пределах 100; десятичный состав числа.

Содержание игры: учитель загадывает загадку “Серебристая пила в небе ниточку вила. Кто же смелый нитью белой небо шил, да поспешил: хвост у нитки распушил?”. Замени число десятками и единицами и в таблице найди буквы. Прочитайте слово и запишите его.

“Гном”

Дидактическая цель: закрепить умение детей заменять двузначное число суммой его разрядных слагаемых.

Содержание игры: Помоги гному найти дорогу к дому. Куда идти: вперёд или назад – об этом числа говорят. Замени каждое число суммой разрядных слагаемых и в таблице найди букву. Составь слово, прочитай.

“По порядку номеров”

Дидактическая цель: закрепление порядка следования чисел при счёте.

Содержание игры: две команды по 10 человек выстраиваются шеренгами лицом к классу. У ведущего – два комплекта карточек разного цвета с числами от 1 до 10 (можно использовать любые варианты чисел). Перед началом игры ведущий перемешивает карточки каждого комплекта и по одной прикрепляет на спины играющих. Ни один из играющих не знает, какое число на его карточке. Узнать это каждый может лишь у своего соседа. По сигналу игроки команд должны построится так, чтобы числа на их карточках были расположены по порядку. Команда, выполнившая задание быстрее и точнее, выигрывает.

“Сбежавшие числа”

Дидактическая цель: усвоение порядка следования чисел в натуральном ряду.

Материал игры: таблички с числами.

Содержание игры:

Учитель вывешивает на доску готовые таблицы (или чертит их на доске), в пустые клетки которых надо вписать пропущенные числа. Ученики должны определить закономерность в записи цифр и вписать нужные. Учитель говорит: “Здесь каждое число живет в своём домике. Но вы видите, что некоторые домики пусты - из них сбежали числа. Какие это числа? Надо подумать и вернуть беглецов в свои дома.” Выигрывает тот, кто вставит числа правильно.

При закреплении темы “Двузначные числа” была проведение игра “Рыболовы”:

Дидактическая цель: анализ однозначных и двузначных чисел.

Содержание игры: на наборном полотне изображен пруд; в прорези полотна вставлены изображения рыбок, на которых написаны двузначные и однозначные числа. Соревнуются две команды по 4 человека в каждой. Поочерёдно каждый член команды “ловит рыбку” (громко называет число) и проводит его анализ: сколько знаков в числе, его место в числовом ряду, разбор чисел по десятичному составу. Если все ответы правильны, то он поймал рыбку (берёт её), если нет – рыбка сорвалась. Выигрывает команда, поймавшая больше рыбок.

При изучении и закреплении темы “Числа от 21 до 100” была использована игра “Весёлый счёт” или “Борьба за цифру”.

Дидактическая цель: закрепление порядка следования чисел.

Средства обучения: два больших листа плотной бумаги, на которых написаны разным цветом цифры большого размера.

Содержание игры: перед каждой таблицей становится один из учеников. Учитель предлагает громко назвать числа по порядку от 1 до 24 и от 52 до 75, одновременно показывая каждое из них на таблице. Тот, кто быстрее назовёт числа, считается победителем. Через каждую таблицу проходит несколько пар.

Пример таблицы:

С помощью этих игр в процессе обучения были не только закреплены знания учащихся, но и активизировано внимание учащихся. С помощью игры “Весёлый счёт” развивалось также и зрительное восприятие детей.

2.4. Особенности применения дидактических игр при обобщении знаний учащихся

На этапе обобщения знаний целесообразно проводить уроки в форме путешествия в сказочную страну или условной экскурсии в лес с элементами игры.

При обобщении темы “Нумерация чисел в пределах 20” можно предложить следующую ситуацию. Класс отправляется на луг ловить бабочек. Начинается игра “Поймай бабочку”:

Дидактическая цель: обобщение знаний о разрядном составе числа.

Содержание игры: на доску вывешивается иллюстрация с изображением луга и макеты бабочек. На каждой бабочке написан разрядный состав чисел до 20. У каждого ребёнка бабочка из картона жёлтого цвета, на обратной стороне которой записаны числа. Один из вызванных к доске учеников ловит бабочку, прикреплённую на ниточке, на которой указан разрядный состав числа, остальные ученики поднимают (ловят) тех бабочек, на которых написаны числа, соответствующие разрядному составу.

Потом все отправляются в магазин, (проголодались на прогулке). Далее проходит игра в “Магазин”:

Дидактическая цель: обобщение знаний учащихся о составе числа.

Содержание игры: вывешивается два плаката: один с рисунками монет, другой с изображением предмета и его ценой (хлеб – цена, батон, булочка, рогалик и т.п.). Дети подходят к плакатам, показывают хлеб, и расплачиваются за покупку набором из существующих монет.

Также при обобщении знаний по теме “Нумерация чисел в пределах 100” можно использовать следующие игры:

“Войди в ворота”

Дидактическая цель: обобщение знаний о составе числа.

Содержание игры: дети берут карточки с числами 0, 1, 2, … , 10. Два ученика образуют ворота (оба поднимают вверх сцепленные руки), в свободных руках они держат карточки с цифрами. В результате образуется несколько пар детей и один лишний. Он входит в ворота, выбирает ученика с такой карточкой, чтобы их числа в сумме составили число 10. Оба ученика проходят назад. Оставшийся без пары ученик также входит в ворота и подбирает пару себе. Все дети сидевшие за столами, следят за правильностью подбора пар.

Учитель школы №147 г.Санкт-Петербурга Е.А.Бочек на уроке обобщения знаний использовала игру-соревнование “Если вместе, если дружно” в 1 классе.[16] Особенность этой игры – эстафетный характер заданий, когда от вклада каждого, от чёткости и взаимодействия зависит общий результат.

Дидактическая цель: развитие логического мышления и воображения, проверка элементарных математических навыков.

Ход игры: учитель объявляет, что урок пройдёт в виде игры под девизом “Если вместе, если дружно”. Класс делится на две команды. Обе команды носят имена великих математиков прошлого: “Пифагоры”, “Архимеды” (желательны эмблемы). Учитель предупреждает, что соревнования будут эстафетными, поэтому будьте готовы проявить взаимопонимание и взаимовыручку.

Эстафета №1 “Очень длинный пример”

На доске написаны примеры. Каждый ученик из команды подбегает к доске по очереди, решает один пример и передаёт эстафету следующему. Кто быстрее и правильнее решит весь пример?

Эстафета №2 “Собери робота”

Участники команд берут из корзин геометрические фигуры (круги, треугольники, квадраты и т.п.) и крепят их на доске так, чтобы получилась фигура, напоминающая робота. У кого робот получится лучше?

Эстафета №3 “Каждому по примеру”

Количество примеров на доске соответствует числу участников команды. Участники команд по очереди подбегают к доске и решают по одному примеру (на выбор). Побеждает команда, которая быстро и без ошибок решит все примеры.

Эстафета №4: “Найди цифру”

На доске два плаката, где в беспорядке прикреплены цифры от 1 до 30. Участники команд по очереди снимают цифры по порядку и составляют числовой ряд. Побеждает команда, первая и правильно построившая полный числовой ряд.

Эстафета №5: “Без права на ошибку”

Команда выстраивается в шеренгу, у каждого в руках листок и карандаш. Ведущий читает задачу:

1. На одной жужаре к нам приехали 15 мямзиков, а на другой – на 7 мямзиков меньше. Сколько мямзиков приехало к нам на второй жужаре?

2. Когда Слюник видит, что кто-то нашёл пусик, он сразу начинает умирать от зависти. В четверг Мряка в присутствии Слюника нашла сначала 6 пусиков, а потом ещё 12 пусиков. Сколько раз Слюник умирал от зависти?

Каждый участник пишет ответ на листочке и показывает жюри, которое отмечает количество правильных ответов и неправильных. Ответ, не показанный до сигнала ведущего, не засчитывается.

Затем выстраивается другая команда и решает следующие задачи:

3. У Кости было 20 больших хрямзиков и 7 маленьких. Когда он узнал, что это такое, он всё побросал и отскочил подальше. Сколько хрямзиков бросил Костя?

4. Волк съел на своём Дне рождения трёх поросят, семерых козлят и одну Красную шапочку. Сколько сказочных героев съел Волк?

Побеждает команда, давшая большее количество верных ответов.

Эстафета №6: “Математическая сказка”

Все участники команды, говоря по одному предложению, продолжают сказку, которую начинает ведущий: первая команда “Однажды в математическом королевстве случилась беда…”, вторая команда “У Пятёрки был День рождения, и она пригласила на него своих друзей…”

После подводятся итоги урока. Какая команда была самая дружная, кому удалось лучше всех справится с трудными математическими заданиями? Награждение. Очень важно, чтобы ученики поняли в процессе игры: если вместе взяться за дело, то даже самые трудные примеры можно решить.

Если такая игра проводится в классе впервые, то учителю надо заранее позаботиться о помощниках (старшеклассниках, родителях), которые при необходимости помогли бы погасить возможные конфликты.

При подведении итогов важно отметить, сколь важны факты оказания помощи, проявления дружбы.

Состав команд в играх-соревнованиях в 1 классе должен меняться в каждой игре, чтобы у участников не появился конкретный постоянный соперник.

Важный педагогический момент игры – помочь учащимся осознать, что учиться вместе легче, чем поодиночке, что у них прекрасные одноклассники, которые всегда помогут.

Также при обобщении знаний детей довольно эффективно проходят игры “Освободи птичку” и “Незадачливый математик”.

“Освободи птичку”

Дидактическая цель: обобщение знания чисел от 21 до 100.

Содержание игры: птички находятся в клетке и учитель предлагает детям выпустить их на волю. Но для этого нужно выполнить задание. Учащиеся берут птичку из клетки и с обратной сторону читают задание (например, посчитай десятками до 60, назови число, в котором 2 дес. и 6 ед, и т.п.). Если ученик правильно ответит на вопрос, то птичка летит (переставляется) на дерево, если нет, то возвращается обратно в клетку.

“Незадачливый математик”

Дидактическая цель: обобщение знаний учащихся о замене числа суммой его разрядных слагаемых.

Средства обучения: кленовые листья, вырезанные из бумаги, с записанными на них числами и знаками, фигура Медвежонка.

Содержание игры: на доске записаны примеры с пропущенными числами и знаками.

Немного в стороне крепятся вырезанные из бумаги кленовые листья с записанными на них цифрами и знаками и иллюстрация Медвежонка.

Учитель предлагает следующую ситуацию: “Ребята, Медвежонок решил примеры на кленовых листочках. Подул ветер и листочки разлетелись. Очень расстроился Медвежонок. Как же теперь быть? Надо помочь ему.” Ребята по очереди выходят к доске, ищут листочки с правильными ответами и заполняют ими пропуски. Данные игры помогают понять, насколько хорошо учащиеся усвоили пройденный материал.

Заключение

В процессе работы над темой на основе рассмотренной нами психолого-педагогической и методической литературы по данному вопросу, а также в результате исследования, мы пришли к выводу, что в педагогической работе большое внимание уделяется дидактической игре на уроке и выявлено её существенное значение для получения, усвоения и закрепления новых знаний у учащихся начальных классов.

Проведя и проанализировав наши исследования, мы выявили, что дидактическая игра позволяет не только активно включить учащихся в учебную деятельность, но и активизировать познавательную деятельность детей. Игра помогает учителю донести до учащихся трудный материал в доступной форме. Отсюда можно сделать вывод о том, что использование игры необходимо при обучении детей младшего школьного возраста на данном конкретном уроке.

В ходе проделанной нами работы, мы сделали вывод, что дидактическая игра может быть использована как и на этапах повторения и закрепления, так и на этапах изучения нового материала. Она должна в полной мере решать как образовательные задачи урока, так и задачи активизации познавательной деятельности, и быть основной ступенью в развитии познавательных интересов учащихся.

Дидактические игры особенно необходимы в обучении и воспитании детей младшего школьного возраста. Благодаря играм удаётся сконцентрировать внимание и привлечь интерес даже у самых несобранных учеников. Вначале их увлекают только игровые действия, а затем и то, чему учит та или иная игра. Постепенно у детей пробуждается интерес и к самому предмету обучения.

Таким образом, дидактическая игра – это целенаправленная творческая деятельность, в процессе которой обучаемые глубже и ярче постигают явления окружающей действительности и познают мир.

Литература

1. Аникеева Н.Б. Воспитание игрой. – М., 1987

2. Амонашвили Ш.А. В школу – с шести лет. – М., 1986

3. Бочек Е.А. Игра-соревнование “Если вместе, если дружно” //Начальная школа, 1999, №1.

4. Выготский Л.С. Педагогическая психология. – М., 1991

5. Жикалкина Т.К. Система игр на уроках математики в 1 и 2 классах. – М., 1996

6. Карпова Е.В. Дидактические игры в начальный период обучения. – Ярославль, 1997

7. Коваленко В.Г. Дидактические игры на уроках математики. – М., 1990

8. Кружецкий В.А. Психология. – М., 1986

9. Кушнерук Е.Н. Занимательность на уроках математики в начальных классах. – Минск, 1987

10. Менджерицкая Д.В. Воспитателю о детской игре. – М., 1982

11. Минскин В.И, От игры к знаниям. – М., 1988

12. Перова М.Н. Дидактические игры и упражнения по математике. – М., 1996

13. Попова В.И. Игра помогает учиться. //Начальная школа, 1987, №2.

14. Перокова О.И., Сазанова Л.И. Раз, два, три – отвечай. – М., 1993

15. Психолого-педагогические особенности проведения дидактических игр. Под.ред. Акшиной А., Акшиной Т., Жарковой Т. – М., 1990

16. Сухомлинский В.А. О воспитании. – М., 1985

17. Чилинрова Л.А., Спиридонова Б.В. Играя, учимся математике. – М., 1993

18. Щедровицкий Г.П. Методические замечания к педагогическим исследованиям игры. // Психология и педагогика игры дошкольников. Под.ред.Запорожца – М.,1996

19. Эльконин Д.Б. Психология игры – М., 1978

20. Новосёлова С.Л. Игра дошкольника. – М., 1989

Приложения

Приложение 1

Анкета №1

Проводится с целью выявления отношения учителя к игре

1. Какое место, по Вашему мнению, занимает игра в развитии личности ребёнка в современных условиях?

- главное,

- не самое главное,

- второстепенное,

- никакого места не занимает,

- не задумывалась над этим,

- не знаю.

2. Сколько времени Вы в своей педагогической деятельности отводите дидактическим играм в учебном процессе?

- очень много,

- не очень много,

- только на уроках математики,

- сегодня это не нужно,

- не задумывалась над этим,

- не знаю.

3. Какие трудности в проведении дидактических игр Вам мешают больше всего?

- отсутствие необходимых условий,

- равнодушие детей,

- не задумывалась над этим,

- не знаю,

- нет.

Приложение 2

Анкета №2

Проводится с целью выявления отношения детей к игре на уроке

1. Какие уроки ты больше всего любишь?

- с использованием таблиц, схем, рисунков,

- главное, чтобы было интересно,

- с использованием игры,

- урок он и есть урок, хоть что, всё равно скучно,

- не люблю любые уроки,

- не знаю, мне всё равно.

2. Если бы ты был учителем, чего бы у тебя было больше на уроке?

- таблиц, схем, рисунков,

- разных игр,

- самостоятельных работ,

- работ с учебником,

- индивидуальной работы по карточкам.

3. Как часто в вашем классе на уроках бывают игры?

- очень часто,

- часто,

- не очень часто,

- изредка,

- никогда.

4. Как ты относишься к игре на уроке?

- очень хочется участвовать,

- нет большого желания поддерживать игру,

- игра на уроке - пустая трата времени.

5. Как ты думаешь, какая польза от игры на уроке?

- очень большая,

- большая,

- не очень большая,

- небольшая,

- никакой пользы,

- не знаю.

Приложение 3

Конспекты уроков математики в 1 классе

Тема: “Числа от 21 до 100 (закрепление)”.

Цель: закрепить умение считать десятками, продолжить формирование понятия о поместном значении цифры, закрепить умение считать в пределах 100; развивать умение анализировать, грамотную математическую речь; поддерживать интерес детей к урокам математики.

Оборудование: карточки с числами (у каждого ученика), таблица чисел.

Содержание урока:

Тема : Сложение и вычитание двузначных чисел в пределах 100.

Цели: 1. Закрепить навыки сложения и вычитания двузначных чисел без перехода через десяток в пределах 100. 2. Развивать умение решать задачи изученных видов, навыки логического мышления. 3. Пробуждать интерес к предмету через дидактическую игру, логические задания.

Оборудование : рисунки с изображением Иван – Царевича, Змея Горыныча, Кощея; карточки с числами и буквами, орнамент из цифр для каллиграфической минутки, листки с примерами для групповой работы.

План:

1. Оргмомент.

2. Объявление темы урока.

3. Каллиграфическая минутка.

Какая цифра спряталась в орнаменте?

Пропишем её¸. 2 2 2 2.

4. Устный счёт .

В некотором царстве, в Тридевятом государстве жили-были Иван-Царевич и Василиса Прекрасная. Однажды Василиса исчезла. Иван-Царевич потужил, погоревал и отправился на поиски. Но куда идти, где искать? Кто похитил Василису? Мы узнаем выполнив первое задание.

1) Найдите “лишнее” число; расположите числа в порядке убывания. Теперь перевернём карточки. Что получилось? 35, 73, 33, 40 , 13, 23.

Иван-Царевич отправился в путь. Но его уже поджидает Змей Горыныч, посланный Кощеем. Кто сразится со Змеем? Нужно победить все три головы Змея.

2) Индивидуальное задание у доски(3 человека).

38+2 65+5 28+2

46-4 87-3 39-6

46+40 87+10 39+30

82+8 56+6 76+4

100-20 50+30 90-40

75-5 91-90 83-3

59-30 36-2 49-3

59-3 36-20 49-30

Поведет Ивана-Царевича волшебный клубочек, но до него нужно добраться по лабиринту чисел (по возрастанию).

3) “Лабиринт”.

4) Волшебный клубочек привёл Ивана-Царевича на распутье. На придорожном камне надпись: “Верная дорога та, где ответ не самый большой и не самый маленький”. По какой дороге идти Ивану?

5) а) А на дороге числа записаны рядами. Найдите закономерность, продолжите ряды чисел:

20, 17, 14, …, …, …, …

2, 4, 7, 11, …, …, …, …

б) Проверка индивидуального задания.

Ребята победили Змея Горыныча. Он охранял сундук, в котором находился меч для Ивана-Царевича. Но сундук крепко заперт тремя замками. А замки не простые - на каждом пример. Что скажете?

Замки откроются, если мы исправим ошибки, сделаем их невидимками. Стирать ничего нельзя, можно дописывать числа и знаки действия.

46=50 28+1=30 64>70

4+46=50 1+28+1=30 64>70-7 и др. числа до 70

46=50-4 28+1=30-1 любое число >6+64>70

Итак, меч в руках Ивана, путь в царство Кощея свободен!

1. Решение примеров на сложение и вычитание. Работа в парах.

Замок Кощея находится на огромной высокой скале. Поможем Ивану-Царевичу преодолеть скалу, решив примеры.

Работаем в парах, помогаем друг другу. Результаты пишем поочерёдно карандашами разного цвета.

2. Решение задачи .

Ну вот и добрались до Кощея. Он встретил Ивана-Царевича такими словами: “Раз ты смог до меня добраться, выполни мои задания, и Василиса – твоя! Если не выполнишь голова с плеч! Вот первое задание.

В моём саду растёт волшебная яблоня с золотыми и серебряными яблоками. Золотых яблок было 12, серебряных 8. 9 яблок я сорвал. Сколько осталось яблок?”

а) Запись краткого условия, разбор задачи, составление графической схемы.

Было – 12 яблок и 8 яблок.

Сорвал – 9 яблок.

Осталось – ?.

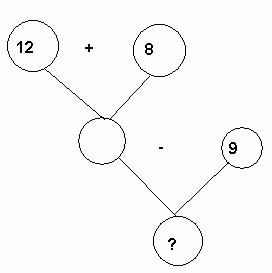
б) Самостоятельное решение задачи

в) Проверка, вписывание чисел в схему.

7. Самостоятельная работа.

1) Решение примеров.

60 – 5 30 – 8 33 + 7 58 + 2 – 4

40 – 7 52 – 30 80 – 5 78 + 20 – 6

2) Фронтальная проверка.

55 22 40 56

33 22 75 92

В каком примере ответ – круглое число?

В каких ответах одинаковое количество десятков и единиц?

Какие ответы не назвали?

8. “Ну, Иван, забирай Василису, - сказал Кощей. – Только сначала догадайся, где она. У меня четыре башни. Первая башня пустая. Василиса не в самой высокой башне. Где она?”

9. Итоги урока.

Тема: Письменные приёмы вычитания двузначных чисел вида 50-32.

Цель: Закреплять приёмы письменного вычитания двузначных чисел вида 50-32; отрабатывать вычислительные навыки; повторение устной и письменной нумерации чисел в пределах 100; развивать умение решать задачи изученных видов; навыки логического мышления; воспитывать познавательную активность.

План :

1. Оргмомент.

2. Сообщение темы урока.

– Сегодня на уроке мы закрепляем приёмы письменного вычитания, когда надо от круглого числа отнять двузначное число, отрабатывать вычислительные навыки и решать задачи изученных видов.

В этом нам сегодня поможет электронно-вычислительная машина – компьютер.

3. Устный счёт.

- уменьшаемое 40, вычитаемое 5. Найти разность.(35)

- увеличить 36 на 15.(51)

- уменьшить 70 на 14.(56)

- найти сумму чисел 26 и 16.(42)

- первое слагаемое 40, второе 21. Сумма.(61)

Задача: Маша гостила у бабушки 4 недели и 5 дней. Сколько дней гостила Маша у бабушки?(33)

Получился ряд чисел: 35 51 56 42 61 33 (числа выставлены на мониторе).

Тестирование . 35 51 56 42 61 33

1. Отметьте число, в котором 5 ед. (35)

2. Отметьте число, которое стоит между числами. 35 и 56 (51)

3. Отметьте число, которое следует за числом 51 (56)

4. Отметьте число, в котором количество единиц на 2 меньше, чем десятков. (42)

5. Отметьте число, в котором 6 дес. (61)

6. Отметьте число, наименьшее в данном ряду. (33)

7. Отметьте число, наибольшее в данном ряду. (61)

8. Отметьте число, в котором 4 дес. 2 ед. (42)

9. Отметьте число, в котором 5 дес. 6 ед. (56)

10. Отметьте число, в котором количество дес. равно количеству ед. (33)

Уч-ся 1 “А” класса ___________________

4. Работа по теме .

_80 (пример на мониторе)

56 - Ребята, проверьте решение примера.

34 - Что-то случилось с нашим компьютером, произошли сбои в системе.

- Объяснить алгоритм решения и исправить ошибку (на мониторе выставляется правильно решённый пример). Ученик решает пример у доски.

а) Решение примеров с комментированием.

_60 _80 _90

42 24 53

б) Самостоятельно по вариантам.

1 вариант

_60 _40 _60 _70 - Назовите пример в ответе которого

46 12 19 38 наименьшее число (14)

14 28 41 32 - Наибольшее число (41)

- Назовите пример, в ответе которого количество единиц на 6 больше, чем десятков. (28)

- В каком примере в ответе 3 дес. 2 ед.? (32)

2 вариант

_60 _80 _70 _90 - Назовите пример в ответе, которого

21 47 25 23 одинаковое количество десятков и единиц (33) 39 33 45 67 - Назовите пример с наибольшим числом в ответе. (67)

- Назовите пример, в ответе которого 4 дес. 5 ед. (45)

5. Физкультминутка (для глаз)

6. Составление и решение задач.

I эт. – 30 чел.<---------------------------

| ?

II эт. – ? на 12 чел. меньше, чем на |

а) Задача: На первом этаже живут 30 человек, а на втором на 12 человек меньше. Сколько человек живут на двух этажах?

1) 30 – 12 = 18 (ч)

2) 30 + 18 = 48 (ч)

Анализ задачи.

- Можем ли сразу ответить на вопрос задачи? (нет)

- Почему? (не знаем сколько на II этаже)

- Что сказано про II этаж? (на 12 ч. <)

- Можем узнать сколько на II этаже? (да)

- Каким действием? (вычитанием)

- Почему? (находим меньшее число)

- Теперь можем ответить на вопрос задачи? (да)

- Каким действием? (сложением) – Почему?

- Какой вид задачи? (составная задача на нахождение суммы)

- Так сколько человек живут на 2-х этажах? (48)

б) Самостоятельное решение задачи.

В одной корзине 37 лимонов, а в другой 33 лимона. Продали 24 лимона. Сколько лимонов осталось?

1) 37 + 33 = 70 (л)

2) 70 – 24 = 46 (л)

Проверка фронтально:

- Что узнали в 1-ом действии? Каким действием?

- Во втором? Каким действием?

в) Задача, которая будет на карточке.

В парке 90 деревьев. Из них 37 лип, 36 клёнов, а остальные – дубы.

Сколько дубов в парке?

1) 37 + 36 = 73 (лип и клёнов)

2) 90 – 73 = 17 (дубов)

- Проверка: один ученик рассказывает условие и решение задачи.

- Поднимите руку, кто так же решил задачу.

7. Геометрический материал.

На мониторе письмо:

Я долго смотрю на эти рисунки и не могу понять, сколько тут спряталось фигур. Помогите. - Поможем? Да.

1 вариант. – Так сколько же здесь спряталось фигур? (6)

- К доске выходит один ученик и показывает эти фигуры (у каждого ученика на столе такой рисунок).

2 вариант. – Сколько треугольников спряталось в данной фигуре?

12 треугольников.

- Один ученик показывает у доски.

8. Итог урока.

- Сначала вашу работу оценит компьютер. Для этого вам надо выполнить следующие вычисления:

_30 _40 _50 _60 _70 _80 _90

11 22 33 44 55 66 77

19 18 17 16 15 14 13

м о л о д ц ы

- Так оценил вашу работу компьютер.

- А сейчас вы сами оцените свою работу.

- На карточках, где проводился тест, с обратной стороны нарисуйте маску настроения (карандашом).

работал хорошо работал неплохо работал плохо

- Поднять карточки и показать.

9. Домашнее задание. Необычно.

- Вы сами его определите, решив следующие числовые выражения.

60 + 40 = 100 Задача. 60 – 40 – 9 = 11

49 – 9 = 40 Примеры. 42 – (20 + 10) = 12

25 – 20 = 5 1 вариант. (столбики) 2 вариант.

Страница 145 26 – 25 = 1 37 – 35 = 2

20 – 17 = 3 30 – 26 = 4

Урок-путешествие в страну занимательной арифметики

Тема: Путешествие с Буратино в страну занимательной арифметики.

Цель: Закрепить у детей умения выделять сходства и различия в предметах; закрепить математические понятия “сумма”, “разность”, а также понятия “большой”, “узкий” и т.д., закрепить знания о свойствах геометрических фигур, о составе числа; совершенствовать навыки устного счёта, закрепить умения составлять и решать простые задачи; развивать внимание, наблюдательность, смекалку.

Игровой материал: игрушка Буратино, конверт с письмами, картинки героев сказки, плакаты Буратино, квадрат с цифрами, мяч, аквариум с рыбками, плакаты с задачами, плакат и геометрические фигуры, плакат с ключом и замками, карточки с числами и буквами; грамзапись сказки “Приключения Буратино”.

Ход урока

Учитель. Добрый день, ребята! Сегодня, когда я шла к вам на урок, мне повстречался один весёлый человек, которого, я надеюсь, вы очень хорошо знаете. Он–то и передал для вас большой конверт, но попросил вручить его только после того, как вы отгадаете загадку о нём

Он из полена вдруг возник

Весёлый, юный озорник,

Ребята, не сочтя за труд,

Скажите, как его зовут?

(Дети отвечают хором: Буратино!)

Правильно, ребята! Молодцы! Действительно, этот весёлый человек и есть герой сказки “Золотой ключик” и зовут его Буратино. А вот и он сам! (учитель показывает игрушку Буратино). Ребята, а давайте вспомним, каких ещё героев этой сказки вы знаете? (ребята перечисляют оставшихся героев). Молодцы, ребята! Вы прекрасно знаете сказку “Золотой ключик”. А теперь самое время вскрыть конверт, который для вас прислал Буратино (на конверте: “ученикам 1 “А” класса СШ №121 от Буратино”). Письмо Буратино:

“Дорогие мои друзья-школьники

Я очень рад, что вы знаете сказку “Золотой ключик” так хорошо, из неё я пришёл к вам. Большое вам спасибо! Пишу это письмо и хочу обратиться к вам за помощью. Герои сказки прислали мне свои задания по математике, которые мне нужно решить. А так, как я не пошёл в школу и умею считать только до 5, то прошу вас помочь мне решить эти задачи! Заранее вам благодарен! Желаю успеха! Буратино”.

Учитель . Ну, что, ребята, отправимся с вами в страну занимательной арифметики и выручим Буратино! А для того, чтобы ему помочь, вы должны быть ловкими, активными, внимательными и смекалистыми, помогать друг другу хорошо считать. Итак,…

I задание. Пудель Артемон.

Милый пёсик Артемон

Встал на задних лапах…

Перед ним два мальчика

В шортиках и шапках.

Пудель смотрит, он притих, даже кость не гложет,

Но что разного у них – он понять не может!

Учитель . А сейчас, ребята, посмотрите на эти рисунки внимательно и помогите понять Артемону, что разного у этих мальчиков. (плакаты с изображением Буратино, у него ключ в разных руках).

II задание. Мальвина.

Раз, два, три, четыре, пять.

Научились вы считать.

Повнимательней сидите

И задачки вы решите.

Учитель . Ребята, Мальвина приготовила для вас занимательные задачки в стихотворениях. Слушайте их внимательно и считайте.

Вышла курочка гулять и взяла своих цыплят.

Семь бежало впереди, три осталось позади.

Беспокоится их мать и не может сосчитать.

Сосчитайте – ка, ребята, сколько было всех цыплят? (10)

Стоит коза, голосит коза: “ Ой, беда, беда, беда!

Разбежались кто куда семеро козлят!

Один в лесок, а второй за стог.

Третий спрятался в бочонок!”

А сколько козлят в избушке сидят? (4)

1, 2, 3, 4: кто живет у нас в квартире?

Мама, папа, брат, сестра, кошка Мурка,

Два котёнка, мой щегол, сверчок и я.

Вот и вся моя семья. (10)

2 цыплёнка стоят, 2 в скорлупках сидят;

6 яиц под крылом у наседки лежат.

Сосчитай поверней, отвечай поскорей,

Сколько будет цыплят у наседки моей! (10)

Сидят рыбаки, стерегут поплавки.

Рыбак корней поймал 10 окуней.

Рыбак Евсей – 7 карасей.

А рыбак Михаил трёх сомов изловил.

Сколько рыб из реки натаскали рыбаки? (20)

Посадила бабка в печь пироги с капустой печь

Для Наташи, Вовы, Коли – пироги готовы.

Да ещё один пирог кот под лавку уволок.

Да в печи – четыре штуки – пироги считают внуки.

Если можешь – помоги, сосчитай-ка пироги! (8)

III задание. Лиса Алиса.

На улице Бассейной

Жила одна лиса

И иногда рассеянной неделями была.

Учитель . Ребята! Лиса Алиса забыла, как нужно расставить в пустые клеточки числа так, чтобы в сумме по всем направлениям было 9.

IV задание. Кот Базилио.

Поспела новая игра,

Нелёгкое задание.

За дело взяться вам пора и проявить старание!

Учитель . Дети, кот Базилио предлагает вам игру “Наоборот”. Кому-то из вас я бросаю мяч и называю слово. А вы поймав мяч, говорите мне противоположное по значению слово и возвращаете мяч. Примеры: толстый-тонкий, утро-вечер, раньше-позже и т.д.

V задание. Черепаха Тортилла.

Вот ещё одна задача.

Ждёт смышлёного удача.

1, 2, 3, 4, 5 – задачу эту вам решать.

Учитель . Дети, внимательно посмотрите и скажите, есть ли среди этих рыбок в аквариуме одинаковые? (решение примеров).

Детям предлагаются следующие примеры (понятия “сумма” и “разность”):

13 + 6 = 19 14 + 3 = 17 19 – 9 =10

11 + 9 = 20 16 + 2 = 18 15 – 4 = 11

12 + 4 = 16 16 – 3 = 13 20 – 10 = 10

15 + 5 = 20 17 – 5 = 12 18 – 6 = 12

Физкультминутка “Лягушки”

Встанем, дети, скажем тихо: 1, 2, 3, 4, 5.

Приподнялись, чуть присели и соседа не задели.

А теперь придётся встать.

На болоте две лягушки

Утром рано умывались,

Полотенцем растирались.

Ножками топали, ручками хлопали.

Вправо – влево наклонялись

И обратно возвращались

Вот здоровья в чём секрет.

Всем друзьям физкультпривет!

VI задание. Пьеро.

Пьеро – поэт рассеянный

Жил на улице Бассейной.

И такие вот задачки

Сочинял для вас, ребятки.

Ответ: на 4 больше?

Ответ: на 3 меньше?

Составление задач по рисунку проводится по следующей схеме. Учитель спрашивает, из каких частей состоит задача, что нам известно из задачи, что значит больше (меньше), каким действием будем решать задачу, почему; затем даётся решение задачи (ответ).

На правило вычитания можно дать такие задачи:

Четыре воробушка спустились на грядки,

Скачут и что-то клюют без оглядки.

Котик-хитрюга внезапно подкрался,

Мигом схватил одного и умчался.

Вот как опасно клевать без оглядки.

Сколько теперь их осталось на грядке?

1, 2, 3, 4, 5 – кошка учится считать

Потихоньку, понемножку приближаем к мышке кошку.

Получаем мы ответ: кошка есть, а мышки нет.

VII задание. Папа Карло.

Очень трудное задание

Ожидает мальчиков.

1,2,3,4,5-

Задачу эту вам решать!

Учитель. Ребята! Вы все знаете, что в каморке у папы Карло на стене висел старый холст с изображением огня и чана, где варилась похлёбка. Вот однажды, когда Буратино ушёл в театр, крыса Шушара прогрызла холст. Сосчитайте, сколько дыр она сделала в холсте? Возьмите фигуры и помогите Буратино заштопать холст. Но будьте внимательны! (какими свойствами обладает геометрическая фигура?)

Учитель предлагает детям рассмотреть фигуры, расположенные по рядам, и ответить на вопросы, какая фигура есть в каждом ряду, как она называется и почему.

VIII задание. Карабас Барабас.

Кто в соревнованьи победит

Конечно, лучший эрудит!

У меня сомнений нет –

Вы дадите мне ответ.

Учитель. Ребята, осталось самое последнее, самое трудное и ответственное задание – освободить Буратино, которого закрыл в домике Карабас Барабас. Посмотрите внимательно на ключ и подумайте, к какой замочной скважине он подойдёт?

I Х задание. Буратино.

Учитель (от имени Буратино). Молодцы, ребята! Вы спасли меня и выполнили все задания героев сказки. Вы очень хорошо играли, поэтому я вам приготовил небольшой сюрприз.

Вам числа выданы не зря, несложен их ответ.

Из них узнаете, друзья, мой небольшой секрет.

(Какие числа называются чётными, нечётными).

лод ти но мо ра цы Бу

( Открыть в порядке возрастания: сначала чётные, затем нечётные).

Читаем вместе: Молодцы, Буратино. Письмо Буратино:

“Дорогие мои друзья-школьники!

Большое спасибо за помощь, которую вы мне оказали в решении сложных математических задач. Следующей осенью я тоже пойду в школу, чтобы стать таким умным, как вы.

Знаю – кто уроки учит,

Ключик золотой получит.

С ним в мир знаний, мне поверь,

Ты всегда откроешь дверь! Буратино.

[1] Сухомлинский В.А. О воспитании. М., 1985 стр.93

[2] Эльконин Д.Б. Психология игры. М., 1978 стр.277

[3] Амонашвили Ш.А. В школу – с шести лет. М., 1986 стр.160

[4] Щедровицкий Г.П. Методические замечания к педагогическим исследованиям игры. // Психология и педагогика игры дошкольников. Под.ред.Запорожца М.,1996 с.24

[5] Эльконин Д.Б. Психология игры М., 1978 стр.57

[6] Чилинрова Л., Спиридонова Б. Играя, учимся математике. М., 1993 стр.6

[7] Коваленко В.Г. Дидактические игры на уроках математики. М., 1990 стр.12-13

[8] Психолого-педагогические особенности проведения дидактических игр. Под.ред. Акшиной А., Акшиной Т., Жарковой Т. М., 1990

[9] Кружецкий В.А. Психология. М., 1986 стр.241

[10] Кружецкий В.А. Психология. М., 1986 стр.242

[11] Менджерицкая Д.В. Воспитателю о детской игре. М., 1982 стр.114

[12] Менджерицкая Д.В. Воспитателю о детской игре. М., 1982 стр.125

[13] Кушнерук Е.Н. Занимательность на уроках математики в начальных классах.

[14] Жикалкина Т.К. Система игр на уроках математики в 1 и 2 классах. М., 1996 стр.46

[15] Попова В.И. Игра помогает учиться. //Начальная школа №2, 1987 стр.39

[16] Бочек Е.А. Игра-соревнование “Если вместе, если дружно” 1 класс //Начальная школа №1, 1999 стр.106-107