| Введение
Нестационарные тепловые процессы в электрических машинах имеют место при их эксплуатации. Ими сопровождаются режимы пуска, отключения, торможения, изменения нагрузки и частоты вращения машин. Большое значение процессы нестационарного нагрева имеют при перегрузках по току и напряжению, при частых и затяжных пусках двигателей, а так же при работе их в заторможенном состоянии.
Особенностью нестационарных тепловых режимов, или тепловых переходных процессов, в электрических машинах является их инерционность, проявляющаяся в значительном отставании изменений температуры от электромеханических переходных процессов. Благодаря этому машины могут выдерживать в течение некоторого времени воздействие перегрузок, токов короткого замыкания и других ненормальных условий. Учет тепловой инерционности в расчетах нестационарного нагрева является обязательным условием достоверности результатов.
Повышенная температура электрических машин влияет на долговечность изоляции обмоток, на работу подшипников и др. Повышенная температура обмоток вызывает тепловое старение изоляции, приводящее к необратимому снижению электрической и механической прочности. Правило Монтзингера гласит, что повышение температуры на 8–100
С сокращает срок службы изоляции в два раза.
Основной целью данной работы является создание тепловой модели для выбора асинхронного двигателя по нагреву. Данная модель является упрощенным представлением процессов нагрева и охлаждения двигателя. Суть модели заключается в том, что, задавая характер изменения нагрузки во времени на входе, на выходе имеем кривую изменения температуры меди обмоток или стали статора.
1. Обзор литературы
1.1 Фундаментальные законы теплопередачи
В основе математической модели нагрева двигателя лежит основной закон теплопроводности [1,2,3,4,5], сформулированный Фурье в итоге анализа экспериментальных данных. Данный закон устанавливает количественную связь между тепловым потоком и разностью температур в двух точках тела: количество переданной теплоты пропорционально градиенту температуры, времени и площади сечения F, перпендикулярного к направлению распространения теплоты.
Если количество переданной теплоты отнести к единице времени, то сформулированная зависимость выразится следующим образом:
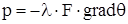 , (1.1) , (1.1)
где р – количество переданной теплоты, отнесенное к единице времени, то есть мощность;
λ – коэффициент теплопроводности;
F – площадь сечения, перпендикулярного к направлению распространения теплоты;
θ – температура точек тела.
Знак «минус» в (1.1) означает, что передача теплоты происходит в сторону, противоположную направлению градиента, то есть в сторону понижения температуры.
Коэффициент теплопроводности λ в уравнении (1.1) является физическим параметром и характеризует способность вещества проводить теплоту.
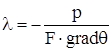 , (1.2) , (1.2)
 . .
Аналитическое решение, полученное путем непосредственного интегрирования уравнения (1.1), дает возможность вычислить температуру в любой точке системы. Однако решение уравнения в частных производных является довольно громоздким и слишком усложняет задачу. Поэтому на практике, для упрощения решения широко используется метод конечных разностей [3]. Сущность метода заключается в том, что в дифференциальном уравнении производные искомой функции заменяются приближенным соотношением между конечными разностями в отдельных узловых точках температурного поля. В результате такой замены получаем уравнение в конечных разностях, решение которого сводится к выполнению простых алгебраических операций:
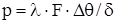 , (1.3) , (1.3)
где δ – расстояние между исследуемыми точками;
Δθ – падение температуры на длине δ.
Для решения задач по определению температурного поля используют дифференциальное уравнение теплопроводности [1,2,3,4], которое выводится на основе закона сохранения энергии и закона Фурье. При выводе уравнения рассматривается нестационарное трехмерное температурное поле в однородном твердом теле, с распределенными по объему источниками теплоты. В пределах рассматриваемого тела берется элементарный объем dV=dx∙dy∙dz (рисунок 1.1), достаточно малый для того, чтобы считать физические параметры в нем постоянными, а потери – равномерно распределенными и пренебречь производными выше второго порядка от температуры θ по координатам.
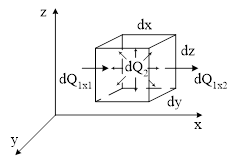
Рисунок 1.1 – Элементарный объем dV
Для элементарного объема dV составляется тепловой баланс за элементарный промежуток времени dt. Тепловой баланс является следствием закона сохранения энергии при допущении, что в энергетическом процессе не участвуют другие виды энергии, кроме тепловой:
 , (1.4) , (1.4)
где dQ1
– тепловой поток, притекающий в объем dV за счет теплопроводности;
dQ2
– мощность источников теплоты, действующих внутри объема;
dQ – повышение внутренней энергии в объеме dV.
На рисунке 1.1 показаны только тепловые потоки, направленные вдоль оси x. Поток, притекающий слева, исходя из закона Фурье:
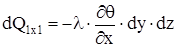 , (1.5) , (1.5)
тепловой поток, проходящий через противоположную грань (с учетом изменения производной ∂θ/∂x на интервале dx):
 . (1.6) . (1.6)
Результирующий приток теплоты за единицу времени вдоль оси x:
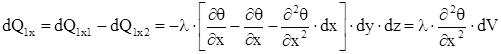 . (1.7) . (1.7)
Аналогично для других координатных осей:
 ; ;  . (1.8) . (1.8)
Суммарный тепловой поток, притекающий в объем dV за счет теплопроводности:
 . (1.9) . (1.9)
Мощность источников теплоты, действующих внутри объема:
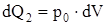 , (1.10) , (1.10)
где р0
– мощность потерь в единице объема.
Изменение внутренней энергии в объеме dV:
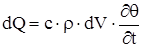 , (1.11) , (1.11)
где с – удельная теплоемкость тела;
ρ – плотность материала тела.
Подставив (1.9), (1.10), (1.11) в (1.4) и проведя некоторые преобразования, получаем дифференциальное уравнение теплопроводности в частных производных:
 . (1.12) . (1.12)
где 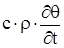 – слагаемое, описывающее изменение теплосодержания тела; – слагаемое, описывающее изменение теплосодержания тела;
 – слагаемое, обуславливающее тепловой поток, притекающий в систему за счет теплопроводности; – слагаемое, обуславливающее тепловой поток, притекающий в систему за счет теплопроводности;
 – слагаемое, обуславливающее внутреннее тепловыделение. – слагаемое, обуславливающее внутреннее тепловыделение.
Рассмотрим процесс нагрева тела с собственным тепловыделением мощностью P, с поверхности S которого происходит теплоотдача конвекцией и излучением при коэффициенте теплоотдачи α [1,3,5]. Для упрощения математического описания процесса вводятся следующие допущения:
1. Тело обладает неограниченной теплопроводностью, что приводит к отсутствию градиента температуры по любому направлению в его объеме.
2. Температура окружающей среды θс
неизменна, то есть окружающая среда обладает неограниченной теплоемкостью.
3. Коэффициент теплоотдачи α между поверхностью машины и окружающей средой не зависит от места и длительности протекания процесса.
Уравнение теплового баланса составляется на том основании, что теплота, выделившаяся за элементарный промежуток времени dt, частично идет на изменение собственного теплосодержания тела и частично отводится в окружающую среду. В соответствии с этим уравнение теплового баланса имеет вид [1,3,5]:
 , (1.13) , (1.13)
где ΔP – выделяемые в данном объеме потери мощности;
θ – температура тела;
θс
– температура окружающей среды;
c – удельная теплоемкость;
G – масса исследуемого объема тела;
α – коэффициент теплоотдачи с единицы площади поверхности;
F – площадь поверхности охлаждения.
В правой части уравнения (1.13) первое слагаемое обуславливает повышение температуры тела, а второе – обмен теплотой с окружающей средой.
После преобразования уравнение теплового баланса (1.13) принимает вид:
 , (1.14) , (1.14)
где C=с∙G – теплоемкость тела;
А=α∙F – коэффициент теплоотдачи тела.
1.2 Обзор методов теплового расчета и существующих моделей
В соответствии с разнообразием условий теплоотвода для теплового расчета электрических двигателей используются различные методы [4]:
1. Метод точного или приближенного аналитического решения уравнений для трех- или двухмерных температурных полей
обычно применяется при значительной неравномерности поля. При этом зачастую требуются определенные упрощения геометрической формы и граничных условий в математической модели.
2. Численный метод сеток
применяется в подобных случаях, но не требует значительных упрощений формы рассчитываемых областей пространства.
3. Метод одномерного температурного поля
применяется для расчета распределения температуры по длине обмоток и других частей электрических машин. Основан на приведении трех- и двухмерных полей к одномерному путем упрощенного представления теплопередачи вдоль всех осей координат, кроме одной, с помощью дискретных параметров (тепловых сопротивлений).
4. Метод эквивалентных тепловых схем (ЭТС)
получил наибольшее распространение ввиду простоты и достаточной точности расчета. Недостаток метода заключается в том, что он дает не полную картину температурного поля, а только некоторые средние значения температуры для отдельных элементов машины.
Данный метод основан на использовании тепловых сопротивлений [1], которые соединяются в тепловую сеть, имитирующую реальные пути передачи тепловых потоков в машине, и предполагает аналогию теплового потока с электрическим током, основанную на одинаковой форме основного закона теплопроводности (закон Фурье) [6]
 (1.15) (1.15)
и электрического тока (закон Ома)
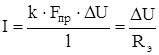 , (1.16) , (1.16)
где Fт
– площадь сечения, перпендикулярного распространению теплоты;
λ – коэффициент теплопроводности;
Δθ – падение температуры на длине δ;
Rт
– тепловое сопротивление данного участка на пути теплового потока;
k – удельная электрическая проводимость;
ΔU – разность потенциалов на длине проводника l с сечением Fпр
;
Rэ
– электрическое сопротивление.
Узлы тепловой схемы имитируют отдельные части двигателя. Если в какой-либо части двигателя присутствуют распределенные по объему источники теплоты, то при составлении эквивалентной тепловой схемы они заменяются сосредоточенным источником (источником теплового потока), помещенным в узел, имитирующий эту часть. Узлы с внутренним тепловыделением на схеме обозначаются кружками, узлы без тепловыделения – точками.
Для детального расчета значений температур используют подробные эквивалентные тепловые схемы. Так, например в [2] приводится тепловая схема закрытого обдуваемого двигателя (рисунок 1.2). Система уравнений для данной схемы в установившемся режиме:
 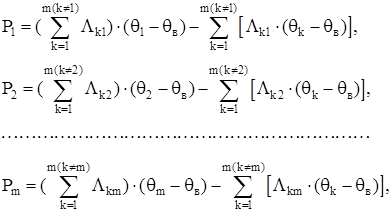 (1.17) (1.17)
где m – количество узлов эквивалентной тепловой схемы;
θв
– температура воздуха снаружи машины;
Λki
=1/Rki
– тепловая проводимость соответствующего участка схемы;
Рi
– потери в i-ом узле.
Отметим, что коэффициент теплоотдачи тела А в (1.14) и тепловые проводимости Λ в (1.17) имеют одинаковый физический смысл и размерность. Для расчета нестационарного режима используется та же тепловая схема, но каждый узел соединяется через емкость с внешним воздухом [4]. В этом случае электрическая емкость эквивалентна теплоемкости тела. Система уравнений для нестационарного режима:
 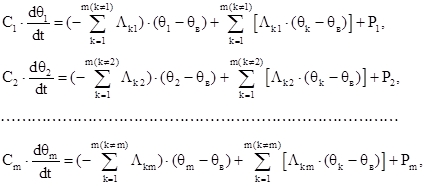 (1.18) (1.18)
где Сi
– теплоемкость соответствующего узла схемы.

 Рисунок 1.2 – ЭТС закрытого обдуваемого двигателя, учитывающая неоднородность температуры корпуса Рисунок 1.2 – ЭТС закрытого обдуваемого двигателя, учитывающая неоднородность температуры корпуса
Однако авторы [4] замечают, что пользоваться подробными схемами с большим количеством узлов целесообразно лишь в редких случаях (например, при проектировании системы охлаждения машины). В практических расчетах конкретных машин удобнее использовать упрощенные эквивалентные тепловые схемы. Упрощения состоят в том, что симметричные узлы подробной схемы, находящиеся в приблизительно одинаковых условиях, объединяются (лобовые части обмотки, воздух внутри машины, подшипниковые щиты) и эквивалентными преобразованиями тепловая схема преобразовывается в схему с меньшим количеством узлов – источников тепловыделения. Объединение узлов, по сути, является заменой нескольких источников тепловыделения, сгруппированных по определенным признакам, в один. Так, в [4,9] предлагается приведенная эквивалентная тепловая схема закрытого обдуваемого двигателя (рисунок 1.3).

Рисунок 1.3 – Приведенная эквивалентная тепловая схема закрытого обдуваемого двигателя
Данная схема имеет шесть узлов: МЛ – лобовая часть обмотки, МП – пазовая часть обмотки, ВВт – воздух внутри машины, Рот – ротор, ССт – сталь сердечника статора, К – корпус двигателя (станина и подшипниковые щиты). Система уравнений нестационарного режима для схемы (см. рисунок 1.3) имеет вид [4,9]:

где Δθм,л
– превышение температуры лобовых частей обмотки;
Δθм,п
– превышение температуры пазовой части обмотки;
Δθс,ст
– превышение температуры стали пакета статора;
Δθрот
– превышение температуры ротора;
Δθв,вт
– превышение температуры воздуха внутри машины;
Δθк
– превышение температуры корпуса;
См,л
– теплоемкость лобовых частей обмотки;
См,п
– теплоемкость пазовой части обмотки;
Сс,ст
– теплоемкость стали пакета статора;
Срот
– теплоемкость ротора;
Св,вт
– теплоемкость воздуха внутри машины;
Ск
– теплоемкость корпуса;
Рм,л
– мощность электрических потерь в лобовых частях обмотки;
Рм,п
– мощность электрических потерь в пазовой части обмотки;
Рс,ст
– мощность потерь в стали статора на вихревые токи и гистерезис;
Ррот
– мощность электрических потерь в роторе;
Рв,вт
– мощность механических и добавочных потерь;
Λа
– тепловая проводимость между лобовой и пазовой частями обмотки;
Λм,с
– тепловая проводимость между пазовой частью обмотки и сердечником статора;
Λм,в-
тепловая проводимость между лобовыми частями обмотки и воздухом внутри машины;
Λрот,в-
тепловая проводимость между ротором и внутренним воздухом; Λрот,с
– тепловая проводимость между ротором и сердечником статора; Λв,к
– тепловая проводимость между воздухом внутри машины и корпусом;
Λс,к
– тепловая проводимость между сердечником статора и корпусом;
Λк
– тепловая проводимость между корпусом и внешним воздухом.
Системы дифференциальных уравнений (1.18) и (1.19), описывающие процессы нагрева двигателя, по сути, являются тепловыми моделями асинхронного двигателя. Основные факторы, определяющие точность расчета по уравнениям (1.18) и (1.19) следующие:
– точность задания источников теплоты, то есть потерь;
– точность определения тепловых проводимостей Λ, которые в свою очередь зависят:
а) от коэффициентов теплопроводности λ, которые подвержены значительному разбросу по технологическим причинам, под влиянием появления воздушных промежутков и т.п.;
б) от коэффициентов теплоотдачи α, поскольку имеющиеся для их определения эмпирические формулы и графики не могут учесть всех влияющих факторов и условий.
В связи с этим, а так же для сокращения объема вычислений, рядом авторов [7,8,9,10,11,12] предложены упрощенные математические модели нагрева асинхронного двигателя.
Так в [7,8] предложена тепловая модель двигателя, состоящая из двух цилиндров (рисунок 1.4).
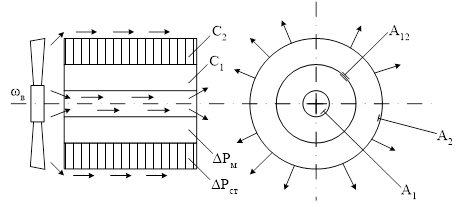
Рисунок 1.4 – Упрощенная модель двигателя как тела нагрева
Внешний цилиндр с теплоемкостью С2
моделирует массу железа машины, внутренний с теплоемкостью С1
– обмотки статора. Мощность теплового потока от стали к окружающей среде пропорциональна коэффициенту А2
. Во внутреннем цилиндре предусмотрен канал, моделирующий отвод теплоты потоками воздуха от внутренних частей машины. Мощность теплового потока от меди статора к окружающей среде пропорциональна коэффициенту А1
. Теплопередача между медью и сталью определяется коэффициентом А12
, моделирующим термическое сопротивление изоляции.
Данной модели соответствует система уравнений [7,8]:
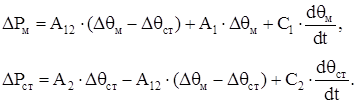 (1.20) (1.20)
где Δθм
и Δθст
– превышения температуры меди и стали соответственно над температурой окружающего воздуха.
В [9] авторы получают уравнения, описывающие поведение температуры обмотки двигателя, путем аналитического решения системы (1.19)
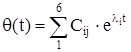 , (1.21) , (1.21)
и замены решения (1.21), состоящего из шести экспонент, приближенным решением, состоящим из двух экспонент:
 , (1.22) , (1.22)
где θ(t) – текущее превышение температуры обмотки;
θуст
– превышение температуры в установившемся режиме;
Ii
– текущее значение тока статора;
Iн
– номинальный значение тока статора;
Tmax
– максимальная постоянная нагрева (постоянная нагрева стали магнитопровода);
Tmin
– минимальная постоянная нагрева (постоянная нагрева обмотки);
Kн
– коэффициент нагрева, учитывающий составляющую превышения температуры стали в превышении температуры обмотки.
По такому же принципу в [9] рассчитывается охлаждение двигателя после отключения его от сети. Зависимость температуры от времени при охлаждении двигателя описывается следующим выражением:
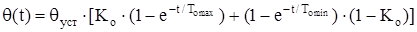 , (1.23) , (1.23)
где To
max
– максимальная постоянная охлаждения;
To
min
– минимальная постоянная охлаждения;
Kо
– коэффициент охлаждения.
Значение θуст
определяется решением (1.19) для установившегося режима, то есть при dθ/dt=0.
По сути дела, в модели [9] двигатель так же представлен двумя телами нагрева: обмоткой статора с минимальной постоянной нагрева Tmin
и сталью машины с максимальной постоянной нагрева Tmax
. Недостатком данной модели является отсутствие задания начальных условий.
Самой простой тепловой моделью электродвигателя является представление его одним телом нагрева [7,8,10,11]. При этом вводятся следующие допущения:
1. Электродвигатель имеет бесконечно большую теплопроводность и, как следствие, одинаковую температуру по всему объему;
2. Количество теплоты, которым электродвигатель обменивается с окружающей средой, пропорционально разности температур двигателя и окружающей среды;
3. Тепловые параметры электродвигателя и окружающей среды постоянны и не связаны с температурой двигателя (это обстоятельство обеспечивает линейность тепловой модели).
В этом случае уравнение, описывающее нагрев двигателя:
 . (1.24) . (1.24)
Решение этого уравнения при постоянстве потерь двигателя ΔP=const и, следовательно, постоянном установившемся превышении температуры:
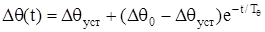 , (1.25) , (1.25)
где Δθ(t) – текущее превышение температуры двигателя над температурой окружающей среды;
Δθуст
– установившееся превышение температуры двигателя;
Δθ0
– начальное превышение температуры двигателя;
Тθ
=С/А – постоянная времени нагрева.
В силу того, что асинхронный двигатель представляет собой сложную термодинамическую систему, неоднородную по своим тепловым параметрам, последняя модель является довольно грубым приближением.
1.3 Патентное исследование
Известны устройства для защиты двигателя от перегрузок, использующие тепловую модель двигателя. Так, например, выдан патент №2192698 на устройство для защиты двигателей. Принципиальная схема устройства приведена на рисунке 1.5.
Это устройство содержит датчик (3) тока для подключения в цепь питания двигателя, квадратор (5), входы которого подключены к выходам датчика тока, тепловой имитатор (6) электродвигателя (тепловую модель), входы которого подключены к выходам квадратора, компаратор (7) и исполнительное реле (8). Тепловой имитатор представляет собой тепловую модель первого порядка, то есть двигатель представлен как однородное тело.

Рисунок 1.5 – Устройство для защиты электродвигателей
В патенте №2192699 описывается устройство для защиты электродвигателя. Принципиальная схема устройства приведена на рисунке 1.6.
Это устройство содержит трансформаторы тока (1, 2, 3), выпрямитель (4), блок (5) контроля перегрузок, блок формирования времятоковой характеристики, состоящий из теплового имитатора (6) электродвигателя, компаратора (7), и исполнительного реле (8). Здесь так же используется тепловая модель первого порядка.

Рисунок 1.6 – Устройство для защиты электродвигателя
2. Выбор и определение параметров тепловой модели асинхронного двигателя
2.1 Выбор тепловой модели
Задача выбора АД по нагреву не требует высокой точности определения температуры меди, которую обеспечивает ЭТС с большим количеством узлов. Поэтому за основу принята модель, представляющая двигатель как два коаксиальных цилиндра [7,8] (см. рисунок 1.4). Основные принципы, на которых базируется модель, рассмотрены в разделе 1.
Данная модель более точно моделирует нагрев двигателя по сравнению с представлением двигателя однородным телом нагрева. В то же время имеется возможность аналитического определения коэффициентов, присутствующих в уравнении (1.20), с достаточной для поставленной задачи точностью.
Перегруппировав неизвестные в уравнениях системы (1.20) получим систему вида:
 (2.1) (2.1)
Системе уравнений (2.1) соответствует ЭТС, изображенная на рисунке 2.1.
В указанной схеме тепловые сопротивления определяются как величины, обратные соответствующим коэффициентам теплоотдачи.
Таким образом, коэффициенты А1
, А12
и А2
возможно определить, приведя эквивалентными преобразованиями тепловую схему замещения асинхронного двигателя к тепловой схеме двухцилиндрической модели.

Рисунок 2.1 – ЭТС, соответствующая двухцилиндрической модели двигателя
2.2 Определение коэффициентов теплоотдачи
2.2.1 Аналитическое определение А1
, А2
, А12
Для определения коэффициентов теплоотдачи рассмотрим упрощенную эквивалентную тепловую схему замещения асинхронного двигателя закрытого исполнения [4,9], (см. рисунок 1.3). Коэффициенты теплоотдачи считаем постоянными, то есть одинаковыми в переходном и установившемся режимах. Следовательно, для их определения можно рассматривать схему (см. рисунок. 1.3) в установившемся режиме (рисунок 2.2), что значительно упрощает решение. Так же введем допущение, что двигатель имеет независимое принудительное охлаждение, то есть коэффициенты теплоотдачи одинаковы при выключенном и включенном двигателе.

Рисунок 2.2 – Приведенная ЭТС закрытого обдуваемого двигателя для стационарного режима
Система уравнений для этой схемы имеет вид [2]:
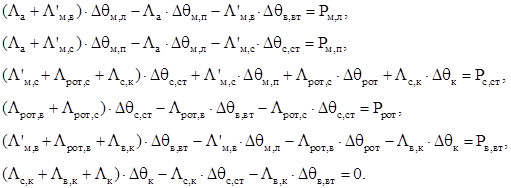 (2.2) (2.2)
Так как в схеме (рисунок 2.2) рассмотрены лобовая и пазовая части обмотки в отдельности, а необходимо знать среднюю температуру обмотки, то по правилам эквивалентных преобразований [4], объединим эти источники в один (рисунок 2.3).

Рисунок 2.3 – Объединение лобовой и пазовой частей обмотки
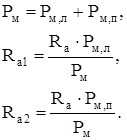
После преобразования (2.3) схема имеет 5 узлов (рисунок 2.4), то есть схеме соответствует система уравнений 5-го порядка.
Объединим сопротивления Ra
1
с R'м,в
и Ra
2
с R'м,с
:
 (2.4) (2.4)
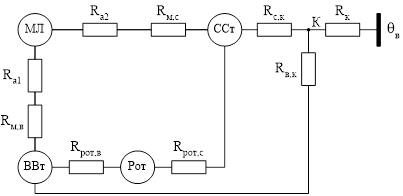
Рисунок 2.4 – ЭТС закрытого обдуваемого двигателя с объединенными пазовой и лобовой частями обмотки
В итоге имеем схему, изображенную на рисунке 2.5 которой соответствует система уравнений (2.5).
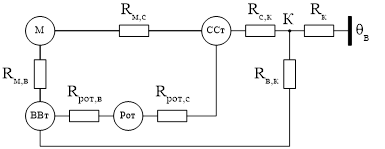
Рисунок 2.5 – Окончательный вид преобразованной ЭТС закрытого обдуваемого двигателя
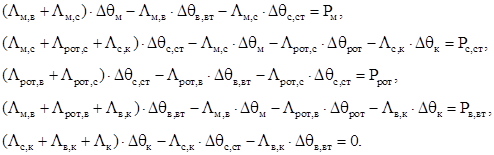 (2.5) (2.5)
Систему уравнений (2.5) необходимо свести к системе уравнений второго порядка, в которой неизвестными выступили бы Δθм
и Δθс,ст
. Для сокращения записи выражений введем замену:
| 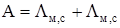 ; ;
|
 ; ;
|
 . .
|
| 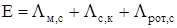 ; ;
|
 ; ;
|
|
| 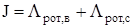 ; ;
|
 ; ;
|
(2.6)
|
|  ; ;
|
 ; ;
|
|
|  ; ;
|
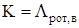 ; ;
|
|
Подставив в (2.5) выражения (2.6), получим:
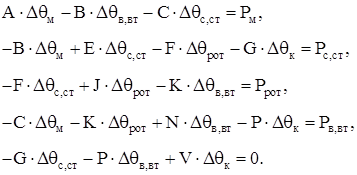 (2.7) (2.7)
Пренебрежем механическими и добавочными потерями (Pв,вт
=0), так как их величина мала по сравнению с основными потерями (потери в меди, стали, роторе) и, как следствие, они незначительно влияют на превышение температуры меди и стали.
Для того чтобы понизить порядок системы (2.7) выразим из последних трех уравнений Δθрот
, Δθв,вт
и Δθк
через Δθм
и Δθс,ст
:
 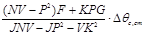 ; (2.8) ; (2.8)
 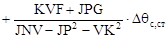 ; (2.9) ; (2.9)
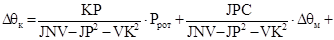 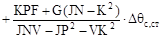 . (2.10) . (2.10)
Подставив выражение (2.9) в первое уравнение системы (2.7) получим:
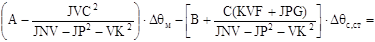 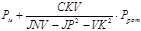 . (2.11) . (2.11)
Для соответствия выражения (2.11) первому уравнению системы (1.20) добавим и вычтем из (2.11) 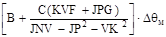 . В результате простых алгебраических преобразований получим уравнение соответствующее первому уравнению системы (1.20): . В результате простых алгебраических преобразований получим уравнение соответствующее первому уравнению системы (1.20):

 . (2.12) . (2.12)
Аналогично поступаем со вторым уравнением системы (2.7). Подставив в него выражения (2.8) и (2.10) получим:
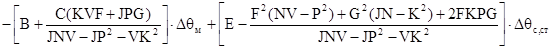
 . (2.13) . (2.13)
Для соответствия выражения (2.13) второму уравнению системы (1.20) добавим и вычтем из (2.13)  . В результате простых алгебраических преобразований получим уравнение соответствующее второму уравнению системы (1.20): . В результате простых алгебраических преобразований получим уравнение соответствующее второму уравнению системы (1.20):

 . (2.14) . (2.14)
Обозначим:
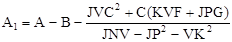 ; (2.15) ; (2.15)
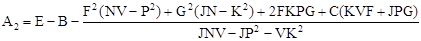 ; (2.16) ; (2.16)
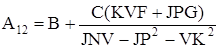 ; (2.17) ; (2.17)
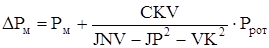 ; (2.18) ; (2.18)
 . (2.19) . (2.19)
Ниже будет показано, что потери в роторе Ррот
пропорциональны току статора, что позволяет объединить Рм
и Ррот
(2.18), Рст
и Ррот
(2.19).
Выражения (2.15) – (2.19) позволяют определить коэффициенты теплоотдачи и потери, необходимые для построения тепловой модели асинхронного двигателя, используя тепловые сопротивления эквивалентной тепловой схемы двигателя.
2.2.2 Расчет тепловых сопротивлений
Тепловые сопротивления для эквивалентной тепловой схемы рассчитываются по методике, приведенной в [2].
1) Сопротивление аксиальное меди статора (тепловое сопротивление между пазовой и лобовой частями обмотки)
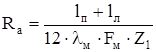 , (2.20) , (2.20)
где lп
– длина паза, м;
lл
– средняя длина одной лобовой части, м;
λм
– коэффициент теплопроводности меди, Вт/(м∙0
С);
Fм
– площадь поперечного сечения меди в пазу, м2
;
Z1
– число пазов статора.
2) Тепловое сопротивление между медью статора и внутренним воздухом
 , (2.21) , (2.21)
где R'л,вш
– тепловое сопротивление внешней (обращенной к станине) продуваемой лобовой части обмотки, 0
С / Вт;
R''л,вш
– тепловое сопротивление внешней (обращенной к станине) непродуваемой лобовой части обмотки, 0
С / Вт;
R'л,вт
– тепловое сопротивление внутренней (обращенной к станине) продуваемой лобовой части обмотки, 0
С / Вт;
R''л,вт
– тепловое сопротивление внутренней (обращенной к станине) непродуваемой лобовой части обмотки, 0
С / Вт.
Тепловое сопротивление между внешней продуваемой лобовой частью обмотки и внутренним воздухом:
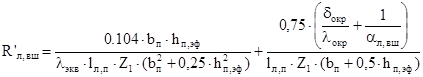 , (2.22) , (2.22)
где bп
– средняя ширина паза, м;
hп,эф
– эффективная по меди высота паза, м;
lл,п
– продуваемая длина лобовой части, м;
δокр
– толщина окраски лобовых частей, м;
λокр
– коэффициент теплопроводности окраски лобовых частей, Вт/(м∙0
С);
Z1
– число пазов статора;
λэкв
– эквивалентный коэффициент теплопроводности обмотки, Вт/(м∙0
С);
αл,вш
– коэффициент теплоотдачи внешней поверхности лобовых частей обмотки статора, Вт/(м2
∙0
С).
Эквивалентный коэффициент теплопроводности обмотки:

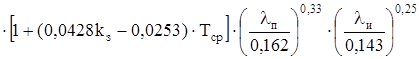 , (2.23) , (2.23)
где kз
– коэффициент заполнения паза;
dи
– диаметр изолированного провода, мм;
kп
– коэффициент пропитки обмотки;
Тср
– средняя температура обмотки;
λп
– коэффициент теплопроводности пропиточного состава;
λи
– коэффициент теплопроводности изоляции проводов.
Коэффициент теплоотдачи внешней поверхности лобовых частей обмотки статора:
 , (2.24) , (2.24)
где λв
– коэффициент теплопроводности воздуха, Вт/(м∙0
С);
Dл,вш
– внешний диаметр лобовой части, м;
Nuвш
– число Нуссельта для внешней поверхности лобовых частей.
Число Нуссельта для внешней поверхности лобовых частей:
 , (2.25) , (2.25)
где Reвш
– число Рейнольдса для внешней поверхности лобовых частей.
Число Рейнольдса для внешней поверхности лобовых частей:
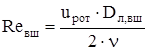 , (2.26) , (2.26)
где uрот
– окружная скорость ротора, м/с;
ν – кинематическая вязкость воздуха, м2
/с.
Тепловое сопротивление между внешней непродуваемой лобовой частью обмотки и внутренним воздухом:
 , (2.27) , (2.27)
где hп,эф
– эффективная по меди высота паза, м;
lл,в-
длина вылета лобовой части обмотки, м.
Тепловое сопротивление между внутренней продуваемой лобовой частью обмотки и внутренним воздухом:
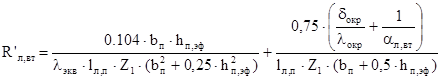 , (2.28) , (2.28)
где αл,вт
– коэффициент теплоотдачи внутренней поверхности лобовых частей обмотки статора, Вт/(м2
∙0
С).
Коэффициент теплоотдачи внутренней поверхности лобовых частей обмотки статора:
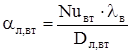 , (2.29) , (2.29)
где Nuвт
– число Нуссельта для внутренней поверхности лобовых частей;
Число Нуссельта для внутренней поверхности лобовых частей:
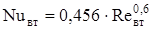 , (2.30) , (2.30)
где Reвт
– число Рейнольдса для внутренней поверхности лобовых частей.
Число Рейнольдса для внутренней поверхности лобовых частей:
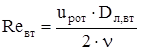 , (2.31) , (2.31)
где Dл,вт
– внутренний диаметр лобовой части, м.
Тепловое сопротивление между внутренней непродуваемой лобовой частью обмотки и внутренним воздухом:
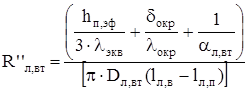 . (2.32) . (2.32)
3) Тепловое сопротивление между медью статора и сердечником статора
 , (2.33) , (2.33)
где Rд,п
– сопротивление отводу теплоты через дно паза, 0
С / Вт;
Rз
– термическое сопротивление зубца, 0
С / Вт;
Rп,з
– тепловое сопротивление между пазовой частью обмотки и зубцами, 0
С / Вт;
Rсп
– сопротивление учитывающее разное сопротивление спинки сердечника собственному и внешнему тепловым потокам, 0
С / Вт.
Сопротивление отводу теплоты через дно паза:
 , (2.34) , (2.34)
где δи,п
– толщина пазовой изоляции, м;
λи,п
– коэффициент теплопроводности пазовой изоляции, Вт/(м∙0
С);
δв,п
– толщина воздушных прослоек (равная половине допуска на укладку), м;
λв,экв
– эквивалентный коэффициент теплопроводности воздушных прослоек в пазу, Вт/(м∙0
С).
Эквивалентный коэффициент теплопроводности воздушных прослоек в пазу:
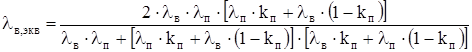 . (2.35) . (2.35)
Термическое сопротивление зубца:
 , (2.36) , (2.36)
где hз
– высота зубца, м;
λс
– коэффициент теплопроводности стали пакета статора, Вт/(м∙0
С);
bз
– средняя ширина зубца, м;
kш
– коэффициент шихтовки (коэффициент заполнения пакета сталью).
Тепловое сопротивление между пазовой частью обмотки и зубцами:
 , (2.37) , (2.37)
где Rвн
– внутреннее сопротивление обмотки, 0
С / Вт;
Rип
– сопротивление пазовой изоляции, 0
С / Вт;
Rвп
– сопротивление воздушных прослоек, 0
С / Вт.
Внутреннее сопротивление обмотки:
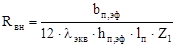 . (2.38) . (2.38)
Тепловое сопротивление пазовой изоляции:
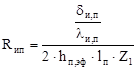 . (2.39) . (2.39)
Тепловое сопротивление воздушных прослоек:
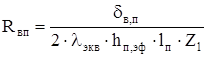 . (2.40) . (2.40)
Тепловое сопротивление спинки сердечника:
 , (2.41) , (2.41)
где Da
– внешний диаметр сердечника статора, м;
Dд,п
– диаметр окружности касательной к дну пазов, м.
4) Тепловое сопротивление между ротором и внутренним воздухом
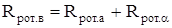 , (2.42) , (2.42)
где Rрот.а
– аксиальное сопротивление отводу теплоты от ротора, 0
С / Вт;
Rрот.α
– конвективное сопротивление отводу теплоты от ротора, 0
С / Вт.
Аксиальное сопротивление отводу теплоты от ротора:
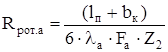 , (2.43) , (2.43)
где λа
– коэффициент теплопроводности алюминия клетки, Вт/(м∙0
С);
Fa
– площадь поперечного сечения паза ротора, м2
;
Z2
– число пазов ротора.
Конвективное сопротивление отводу теплоты от ротора:
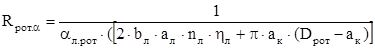 , (2.44) , (2.44)
где αл.рот
– коэффициент теплоотдачи лопаток ротора, Вт/(м2
∙0
С);
bл
– ширина лопатки ротора, м;
ал
– высота лопатки ротора, м;
nл
– количество лопаток ротора;
ηл
– коэффициент качества лопатки ротора, рассматриваемой как ребро;
ак
– высота короткозамыкающего кольца, м;
Dрот
– диаметр ротора, м.
Коэффициент теплоотдачи лопаток ротора:
 , (2.45) , (2.45)
где Nuл
– число Нуссельта для лопаток ротора.
Число Нуссельта для лопаток ротора:
 , (2.46) , (2.46)
где Reл
– число Рейнольдса для лопаток ротора.
Число Рейнольдса для лопаток ротора:
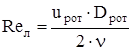 . (2.47) . (2.47)
5) Тепловое сопротивление между ротором и статором
 , (2.48) , (2.48)
где Rδ
– тепловое сопротивление воздушного зазора, 0
С / Вт;
Rз
– термическое сопротивление зубца (2.36), 0
С / Вт.
Тепловое сопротивление воздушного зазора:
 , (2.49) , (2.49)
где аΣ
– коэффициент теплоотдачи от ротора к внутреннему воздуху, Вт/(м2
∙0
С).
Коэффициент теплоотдачи от ротора к внутреннему воздуху:
 , (2.50) , (2.50)
где δ – зазор между ротором и статором, м;
Rрот
=Dрот
/2 – радиус ротора, м.
6) Сопротивление между сердечником статора и корпусом
 , (2.51) , (2.51)
где RΔc
– тепловое сопротивление стыка сердечник станина, 0
С / Вт;
Rсп
– тепловое сопротивление спинки сердечника (2.41), 0
С / Вт.
Тепловое сопротивление стыка сердечник станина:
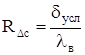 , (2.52) , (2.52)
где δусл
– условный зазор в стыке сердечник станина, м.
Для двигателей серии 4А величина условного зазора приблизительно равна:
δусл
≈(20∙Da
+26) ∙10-6
. (2.53)
7) Тепловое сопротивление между внутренним воздухом и корпусом
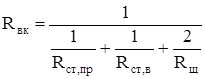 , (2.54) , (2.54)
где Rст,пр
– тепловое сопротивление между внутренней поверхностью станины со стороны привода и внутренним воздухом, 0
С / Вт;
Rст,в-
тепловое сопротивление между внутренней поверхностью станины со стороны вентилятора и внутренним воздухом, 0
С / Вт;
Rщ
– тепловое сопротивление между внутренней поверхностью подшипникового щита и внутренним воздухом, 0
С / Вт.
Тепловое сопротивление между внутренней поверхностью станины со стороны привода и внутренним воздухом:
 , (2.55) , (2.55)
где Fст,пр
– площадь внутренней поверхности свеса станины со стороны привода, м2
;
αс
– коэффициент теплоотдачи внутренней поверхности свесов станины, Вт/(м2
∙0
С).
Площадь внутренней поверхности свеса со стороны привода:
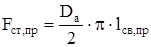 , (2.56) , (2.56)
где lсв,пр
– длина свеса станины со стороны привода, м.
Коэффициент теплоотдачи внутренней поверхности свесов станины:
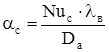 , (2.57) , (2.57)
где Nuc
– число Нуссельта для внутренней поверхности свесов станины.
Число Нуссельта для внутренней поверхности свесов станины зависит от высоты оси вращения и от наличия диффузора в полости лобовых частей.
Для высоты оси вращения h<160 мм:
 , (2.58) , (2.58)
для высоты оси вращения h=160–250 мм:
без диффузора-  ; (2.59) ; (2.59)
с диффузором-  , (2.60) , (2.60)
где Rec
– число Рейнольдса для внутренней поверхности свесов станины;
D – внутренний диаметр сердечника статора, м.
Число Рейнольдса для внутренней поверхности свесов станины:
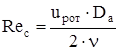 . (2.61) . (2.61)
Тепловое сопротивление между внутренней поверхностью станины со стороны вентилятора и внутренним воздухом:
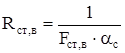 , (2.62) , (2.62)
где Fст,в-
площадь внутренней поверхности свеса со стороны вентилятора, м2
;
αс
– коэффициент теплоотдачи внутренней поверхности свесов станины, Вт/(м2
∙0
С).
Площадь внутренней поверхности свеса со стороны вентилятора:
 , (2.63) , (2.63)
где lсв,в-
длина свеса станины со стороны вентилятора, м.
Тепловое сопротивление между внутренней поверхностью подшипникового щита и внутренним воздухом:
 , (2.64) , (2.64)
где Fщ
– площадь внутренней поверхности подшипникового щита, м2
;
αщ
– коэффициент теплоотдачи внутренней поверхности подшипникового щита, Вт/(м2
∙0
С).
Площадь внутренней поверхности подшипникового щита:
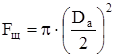 . (2.65) . (2.65)
Коэффициент теплоотдачи внутренней поверхности подшипникового щита:
 , (2.66) , (2.66)
где Nuщ
– число Нуссельта для внутренней поверхности подшипникового щита.
Число Нуссельта для внутренней поверхности подшипникового щита зависит от высоты оси вращения и от наличия диффузора в полости лобовых частей.
Для высоты оси вращения h<160 мм:
 , (2.67) , (2.67)
для высоты оси вращения h=160–250 мм:
без диффузора-  ; (2.68) ; (2.68)
с диффузором-  , (2.69) , (2.69)
где Reщ
– число Рейнольдса для внутренней поверхности свесов станины;
δд,щ
– зазор между диффузором и щитом в месте крепления, м.
Число Рейнольдса для внутренней поверхности подшипниковых щитов:
 . (2.70) . (2.70)
8) Тепловое сопротивление между внешним воздухом и корпусом
 , (2.71) , (2.71)
где Rвс,пр
– тепловое сопротивление между наружной поверхностью свисающей части станины со стороны привода и внешним воздухом, 0
С / Вт;
Rвс
– тепловое сопротивление между наружной поверхностью станины над пакетом и внешним воздухом, 0
С / Вт;
Rвс,в-
тепловое сопротивление между наружной поверхностью свисающей части станины со стороны вентилятора и внешним воздухом, 0
С / Вт;
Rвщ,пр
– тепловое сопротивление между наружной поверхностью подшипникового щита со стороны привода и внешним воздухом, 0
С / Вт;
Rвщ,в-
тепловое сопротивление между наружной поверхностью подшипникового щита со стороны вентилятора и внешним воздухом, 0
С / Вт.
Тепловое сопротивление между наружной поверхностью станины над пакетом и внешним воздухом:
 , (2.72) , (2.72)
где αс,п
– коэффициент теплоотдачи наружной поверхности станины над пакетом, Вт/(м2
∙0
С);
Dc
– диаметр станины у основания ребер, м;
zp
– количество ребер станины;
δр
– толщина ребра станины, м;
hр
– высота ребра станины, м;
ηр
– коэффициент качества ребра станины.
Тепловое сопротивление между наружной поверхностью свисающей части станины со стороны привода и внешним воздухом:
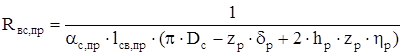 , (2.73) , (2.73)
где αс,пр
– коэффициент теплоотдачи наружной поверхности станины со стороны привода, Вт/(м2
∙0
С).
Тепловое сопротивление между наружной поверхностью свисающей части станины со стороны вентилятора и внешним воздухом:
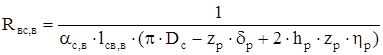 , (2.74) , (2.74)
где αс,в-
коэффициент теплоотдачи наружной поверхности станины со стороны вентилятора, Вт/(м2
∙0
С).
Коэффициент теплоотдачи наружной поверхности станины над пакетом:
 , (2.75) , (2.75)
где αвх
– коэффициент теплоотдачи на входе в межреберные каналы станины, Вт/(м2
∙0
С);
dг
– гидравлический диаметр межреберного канала, м;
γ – коэффициент уменьшения теплоотдачи по длине станины.
Коэффициент теплоотдачи наружной поверхности станины со стороны привода:
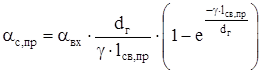 . (2.76) . (2.76)
Коэффициент теплоотдачи наружной поверхности станины со стороны вентилятора:
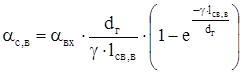 . (2.77) . (2.77)
Гидравлический диаметр межреберного канала:
 , (2.78) , (2.78)
где tр
– шаг ребер станины, м.
Коэффициент уменьшения теплоотдачи по длине станины:
 . (2.79) . (2.79)
Коэффициент теплоотдачи на входе в межреберные каналы станины:
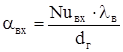 , (2.80) , (2.80)
где Nuвх
– число Нуссельта для межреберных каналов.
Число Нуссельта для межреберных каналов:
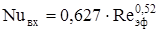 , (2.81) , (2.81)
где Reэф
– число Рейнольдса для межреберных каналов.
Число Рейнольдса для межреберных каналов:
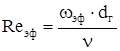 , (2.82) , (2.82)
где ωэф
– эффективная скорость на входе в межреберные каналы, м/с.
Эффективная скорость на входе в межреберные каналы:
 , (2.83) , (2.83)
где ωвх
≈0,45∙uвент
– расходная скорость на входе в каналы, м/с;
uвент
– окружная скорость вентилятора, м/с.
Коэффициент качества ребра станины:
 , (2.84) , (2.84)
 , (2.85) , (2.85)
где λст
– коэффициент теплопроводности материала станины, Вт/(м∙0
С).
Тепловое сопротивление между наружной поверхностью подшипникового щита со стороны привода и внешним воздухом:
 , (2.86) , (2.86)
где αщ,пр
– коэффициент теплоотдачи внешней поверхности подшипникового щита со стороны привода, Вт/(м2
∙0
С).
Коэффициент теплоотдачи внешней поверхности подшипникового щита со стороны привода:
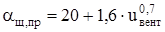 . (2.87) . (2.87)
Тепловое сопротивление между наружной поверхностью подшипникового щита со стороны вентилятора и внешним воздухом:
 , (2.88) , (2.88)
где αщ,в-
коэффициент теплоотдачи внешней поверхности подшипникового щита со стороны вентилятора, Вт/(м2
∙0
С).
Коэффициент теплоотдачи внешней поверхности подшипникового щита со стороны вентилятора зависит от высоты оси вращения.
Для высоты оси вращения h<160 мм:
 , (2.89) , (2.89)
для высоты оси вращения h>160 мм:
 . (2.90) . (2.90)
Как видно, для определения тепловых сопротивлений требуется знать большое количество конструктивных параметров. Ниже приводятся полный перечень необходимых для расчета сопротивлений данных:
Паспортные данные
1. Синхронная частота вращения n1, об/мин;
2. Количество пар полюсов p.
Параметры станины
1. Высота оси вращения h, мм;
2. Диаметр станины у основания ребер Dc
, м;
3. Длина свисающей части станины со стороны привода lсв.пр
, м;
4. Длина свисающей части станины со стороны вентилятора lсв.в
, м;
5. Зазор между диффузором и подшипниковым щитом в месте крепления δд.щ
, м;
6. Количество ребер станины zp
;
7. Высота ребра станины hp
, м;
8. Толщина ребра станины δр
, м.
Параметры вентилятора
1. Внешний диаметр вентилятора Dвент
, м.
Параметры статора
1. Внешний диаметр сердечника Da
, м;
2. Внутренний диаметр сердечника D, м;
3. Длина паза lп
, м;
4. Число пазов статора Z1
;
5. Коэффициент шихтовки (заполнения пакета сталью) kш
=0,97.
Параметры паза статора
1. Большая ширина паза b1
, м;
2. Меньшая ширина паза b2
, м;
3. Высота паза hп
, м;
4. Коэффициент заполнения паза kз
;
5. Высота шлица hш
;
6. Ширина шлица bш
, м;
7. Высота зубца hз
, м;
8. Ширина зубца bз
, м.
Параметры обмотки
1. Количество витков в обмотке фазы ω1
;
2. Число параллельных ветвей а;
3. Средняя длина витка обмотки lср1
, м;
4. Длина вылета лобовой части обмотки с одной стороны lл.в
, м;
5. Диаметр изолированного проводника dи
, мм;
6. Коэффициент пропитки обмотки kп
;
7. Толщина окраски обмотки в лобовой части δокр
, м;
Параметры пазовой изоляции
1. Толщина пазовой изоляции δи.п
, м.
Параметры ротора
1. Внешний диаметр ротора Dрот
, м;
2. Число пазов ротора Z2
;
3. Ширина короткозамыкающего кольца bк
, м;
4. Высота короткозамыкающего кольца aк
, м;
5. Ширина лопатки ротора bл
, м;
6. Высота лопатки ротора ал
, м;
7. Количество лопаток ротора zл
;
8. Коэффициент качества лопатки, рассматриваемой как ребро ηл
;
9. Толщина воздушного зазора между ротором и статором δ, м.
Общие физические величины
1. Кинематическая вязкость воздуха ν, м2
/с;
2. Коэффициент теплопроводности воздуха λв
, Вт/(0
С∙м);
3. Средняя температура обмотки Tср
, 0
С;
4. Коэффициент теплопроводности меди обмотки λм
, Вт/(0
С∙м);
5. Коэффициент теплопроводности алюминия клетки λа
, Вт/(0
С∙м);
6. Коэффициент теплопроводности материала станины λст
, Вт/(0
С∙м);
7. Коэффициент теплопроводности стали пакета статора λс
, Вт/(0
С∙м);
8. Коэффициент теплопроводности пропиточного состава обмотки λп
, Вт/(0
С∙м);
9. Коэффициент теплопроводности изоляции проводов λи
, Вт/(0
С∙м);
10. Коэффициент теплопроводности окраски обмотки в лобовой части λокр
, Вт/(0
С∙м).
Расчет теплоемкостей меди и стали
2.3.1 Определение теплоемкости меди
Теплоемкость меди равна:
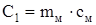 , (2.91) , (2.91)
где mм
– масса меди обмотки статора, кг;
см
– удельная теплоемкость меди обмотки статора, Дж/(кг∙0
С).
Масса меди обмотки статора:
 , (2.92) , (2.92)
где m1
– число фаз обмотки статора;
lср1
– средняя длина витка обмотки статора, м;
w1
– число витков обмотки статора;
а – количество параллельных ветвей обмотки статора;
nэл
– количество элементарных проводников в эффективном;
dпр
– диаметр элементарного проводника, м;
γм
– плотность меди обмотки, кг/м3
.
Определение теплоемкости стали
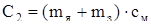 , (2.93) , (2.93)
где mя
– масса ярма статора, кг;
mз
– масса зубцов статора, кг;
сст
– удельная теплоемкость стали пакета статора, Дж/(кг∙0
С).
Масса ярма статора:
 , (2.94) , (2.94)
где γс
– плотность стали пакета статора, кг/м3
.
Масса зубцов статора:
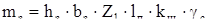 . (2.95) . (2.95)
2.4.1 Потери в обмотке статора
При определении потерь в обмотке статора не учитываем увеличение активного сопротивления пазовой части обмотки статора за счет эффекта вытеснения тока.
Потери в лобовой и пазовой частях обмотки [4]:
 , (2.96) , (2.96)
 , (2.97) , (2.97)
где r1
– активное сопротивление фазы обмотки статора, Ом;
lл
– длина лобовой части обмотки с одной стороны, м;
I1
– ток фазы обмотки статора, А.
Полные потери в меди обмотки статора:
 . (2.98) . (2.98)
Активное сопротивление фазы обмотки статора:
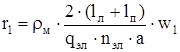 , (2.99) , (2.99)
где ρм
– удельное сопротивление меди обмотки статора при ожидаемой температуре, Ом∙м;
qэл
=π(dэл
/2)2
– площадь поперечного сечения элементарного проводника, м2
.
Ток фазы обмотки статора:
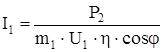 , (2.100) , (2.100)
где Р2
– мощность на валу двигателя, Вт;
η – коэффициент полезного действия, о.е;
cosφ – коэффициент мощности;
U1
– фазное напряжение, В.
2.4.2 Потери в обмотке ротора
Потери в коротозамкнутой обмотке ротора определяются по формуле [13]:
 , (2.101) , (2.101)
где r2
– активное сопротивление фазы обмотки ротора, Ом;
I2
– ток ротора, А.
Активное сопротивление фазы обмотки ротора:
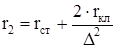 , (2.102) , (2.102)
где rст
– активное сопротивление стержня клетки, Ом;
rкл
– активное сопротивление короткозамыкающего кольца, Ом;
Активное сопротивление стержня клетки:
 , (2.103) , (2.103)
где ρа
– удельное сопротивление алюминия обмотки ротора при ожидаемой температуре, Ом∙м.
Активное сопротивление короткозамыкающего кольца:
 , (2.104) , (2.104)
где Dкл,ср
– средний диаметр короткозамыкающего кольца, м;
qкл
– площадь поперечного сечения короткозамыкающего кольца, м2
.
Коэффициент приведения тока кольца к току стержня:
 , (2.105) , (2.105)
где p – количество пар полюсов.
Ток в обмотке ротора:
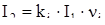 , (2.106) , (2.106)
где ki
– коэффициент, учитывающий влияние тока намагничивания и сопротивления обмоток на отношение I1
/I2
;
νi
– коэффициент приведения токов.
Коэффициент, учитывающий влияние тока намагничивания и сопротивления обмоток на отношение I1
/I2
:
 . (2.107) . (2.107)
Коэффициент приведения токов:
 , (2.108) , (2.108)
где kоб1
– обмоточный коэффициент обмотки статора;
kск
– коэффициент скоса пазов ротора.
2.4.3 Потери в стали пакета статора
При расчете электрических машин потери в стали, определяют через массу стали и удельные потери, которые в свою очередь определяются значением магнитной индукции в стали и частотой питающего напряжения [13,14,15]. Такой способ определения потерь неудобен из-за того, что необходимо знать значение магнитной индукции в сердечнике статора.
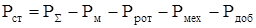 , (2.109) , (2.109)
где РΣ
– суммарная мощность потерь в двигателе, Вт;
Рмех
– мощность механических потерь, Вт;
Рдоб
– мощность добавочных потерь, Вт.
Суммарная мощность потерь в двигателе:
 . (2.110) . (2.110)
Мощность механических потерь [13]:
 , (2.111) , (2.111)
где Кт
– коэффициент механических потерь.
Коэффициент механических потерь для двигателей с 2 р=2
 , (2.112) , (2.112)
при 2 р≥4 Кт
=1.
Мощность добавочных потерь:
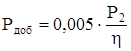 . (2.113) . (2.113)
3. Реализация тепловой модели асинхронного двигателя в программном пакете
Matlab
3.1 Переход к операторной форме
Для решения системы дифференциальных уравнений (1.20) на ЭВМ при помощи приложения Simulink, входящего в состав пакета MatLab, представим ее в операторной форме. Следует заметить, что недостатком приложения Simulink является отсутствие задания начальных условий в блоке передаточных функций. Поэтому при преобразовании (1.20) необходимо учесть начальные условия, то есть начальные температуры меди и стали.
В системе (1.20) присутствуют превышения температур меди и стали, которые равны:
 , (3.1) , (3.1)
 . (3.2) . (3.2)
Подставив (3.1) и (3.2) в (1.20) и раскрыв скобки получим:
 (3.3) (3.3)
Представим систему (7.3) в операторной форме, по правилам преобразования Лапласа:
 (3.4) (3.4)
где θм
(0) – начальная температура меди, 0
С;
θст
(0) – начальная температура стали, 0
С;
Сгруппируем неизвестные θм
(р) и θст
(р) в левых частях уравнений (3.4), а остальные члены в правых частях:
 (3.5) (3.5)
Представим систему (3.5) в матричной форме:
 (3.6) (3.6)
Решим систему (3.6) методом наложения относительно неизвестных θм
(р) и θст
(р). Решение имеет вид:
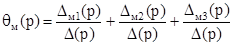 , (3.7) , (3.7)
 , (3.8) , (3.8)
где

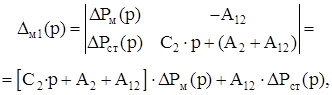

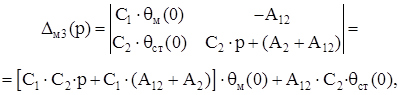
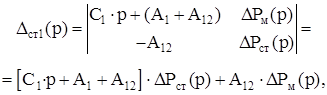
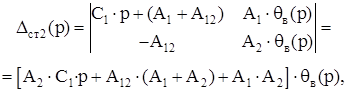
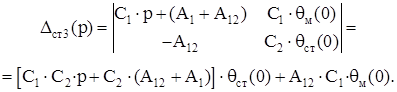
Подставив выражения (3.10), (3.11) и (3.12) в (3.7) получим:
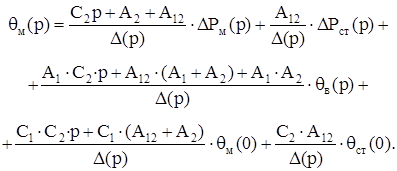
Подставив выражения (3.13), (3.14) и (3.15) в (3.8) получим:

Выражения (3.16) и (3.17) являются окончательным решением для температур меди и стали в операторной форме. Значение Δ в выражениях (3.16) и (3.17) не раскрывается для сокращения записи.
3.2 Синтез структурной схемы тепловой модели асинхронного двигателя
По выражениям (3.16) и (3.17) строим структурную схему модели в приложении Simulink.
Структурная схема для определения температуры меди приведена на рисунке 3.1. Блоки «S1», «S2» и «S3» моделируют различные режимы нагрузки двигателя. Блок «Switch» служит для выбора одного из режимов «S1», «S2» или «S3». Он управляется источником постоянного воздействия «Rezhim». Блок «Poteri» представляет собой подсистему, рассчитывающую потери в двигателе в зависимости от нагрузки. Блоки «Tm(0)» и «Tst(0)» служат для задания начальных температур меди и стали. Блок «Tv» задает значение температуры окружающего воздуха. В блоки передаточных функций «Cu», «Fe», «Cu(0)», «Fe(0)» и «Air» входят коэффициенты выражения (3.16), отражающие вклад каждой задаваемой величины в нагрев обмотки. С выхода передаточных функций сигналы поступают на сумматор «Sum1». На выходе «Sum1» формируется значение температуры меди, которое поступает на виртуальный осциллограф «Scope», регистрирующий прибор «Display» и элемент сравнения «RELE». Блоки «Kriticheskaja temperatura» и «RELE» моделируют работу теплового реле. Блок «Kriticheskaja temperatura» задает предельное значение температуры обмотки статора. Значение температуры обмотки поступает на элемент сравнения и сравнивается с предельным значением, устанавливаемым ГОСТ 183–74 в соответствии с классом изоляции. Так, например, для изоляции класса В предельное значение температуры обмотки θм
=1200
С, для изоляции класса F – θм
=1400
С, для изоляции класса H – θм
=1650
С. Если значение температуры обмотки больше предельного, то на выходе элемента сравнения появляется сигнал, который отображается на индикаторе.
Развернутая структурная схема блока «Poteri» представлена на рисунке 3.2. Она состоит из 20 блоков: «P2», «KPD», «cos(fi)», «Tok statora», «Poteri v medi», «Tok rotora», «Poteri v rotore», «Summarnye poteri», «Dobavochnye poteri», «Mehanicheskie poteri», «Ground», «Relational operator», «Product1», «Sum3», «Sum4», «Sum5», «Gain1», «Gain2», «Pm», «Pst».

Рисунок 3.1 – Структурная схема модели для определения температуры меди
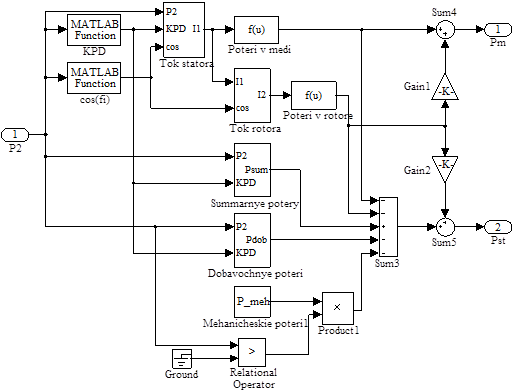
Рисунок 3.2 – Развернутая схема подсистемы «Poteri»
Поясним назначение каждого из блоков.
Блоки «KPD» и «cos(fi)» представляют собой блоки задания функций MatLab, в которых производится кубическая сплайн-интерполяция дискретных значений коэффициента полезного действия η и коэффициента мощности cosφ для определения их величин при произвольном значении нагрузки в интервале 0,25∙Р2
÷ 1,25∙Р2
. В тексте m-файла (см. Приложение А) задаются векторы значений η, cosφ и P2
. Дискретные значения η и cosφ берутся из справочных материалов [17]. По этим значениям MatLab строит функцию, состоящую из отрезков кубических полиномов, так, что каждый отрезок проходит через три узловые точки. Результат интерполяции в узловых точках имеет непрерывные первую и вторую производные. Интерполяция реализуется функцией spline (P_2, cosf, P2), где P_2 – идентификатор вектора значений P2
, cosf – идентификатор вектора значений коэффициента мощности, Р2 – текущее значение мощности для которого необходимо определить cosφ. На рисунке 3.3 приведен график, полученный сплайн-интерполяцией дискретных значений η, приведенных в таблице 3.1, для двигателя марки 4А132М2У3. Крестиками на графике обозначены узловые точки.
Таблица 3.1 – Значения η и cosφ для двигателя марки 4А132М2У3
| Р2
/Р2ном
|
0,25
|
0,5
|
0,75
|
1
|
1,25
|
| Р2
, кВт
|
2,75
|
5,5
|
8,25
|
11
|
13,75
|
| η, %
|
80
|
87
|
88
|
88
|
87
|
| cosφ
|
0,65
|
0,82
|
0,87
|
0,9
|
0,9
|
Аналогично интерполируются значения коэффициента полезного действия. На рисунке 3.4 приведен график, полученный сплайн-интерполяцией дискретных значений cosφ, приведенных в таблице 3.1, для двигателя марки 4А132М2У3. Узловые точки обозначены крестиками.

Рисунок 3.3 – График зависимости η от нагрузки P2
, полученный сплайн-интерполяцией
Блок «P2» (см. рисунок 3.2) обозначает вход подсистемы, блоки «Pm» и «Pst» – выходы.
Блоки «Poteri v medi» и «Poteri v rotore» представляют собой блоки задания алгебраических функций и служат для определения потерь в меди и роторе по выражениям (2.98)

и (2.101)
 . .
Блок «Mehanicheskie poteri» представляет собой источник постоянного воздействия с величиной Pмех
. Он предназначен для моделирования механических потерь в двигателе. Блоки «Ground», «Relational operator» и «Product1» служат для того, чтобы при отсутствии нагрузки Р2
механические потери Pмех
были равны нулю. Величина нагрузки Р2
на элементе сравнения «Relational operator» сравнивается с нулевым значением. Если нагрузка равна нулю, то на выходе элемента сравнения сигнал отсутствует, если не равна нулю, то на выходе элемента сравнения появляется единица. Блок «Product1» перемножает мощность на валу с выходным значением элемента сравнения. При умножении Рмех
на единицу на выходе блока «Product1» имеем величину механических потерь. При умножении Рмех
на ноль на выходе блока «Product1» сигал равен нулю.
Блоки «Gain1» и «Gain2» имеют коэффициент усиления, равный A_rot и B_rot соответственно, и обеспечивают умножение значения потерь в роторе Pрот
на коэффициенты, присутствующие в выражениях (2.18)
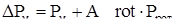
и (2.19)
 . .
Коэффициенты усиления A_rot и B_rot рассчитываются в теле m-файла.
Подсистема «Tok statora» рассчитывает значение тока статора по выражению (2.100)
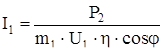 . .
Структурная схема подсистемы приведена на рисунке 3.5.
В блоке «Tok» (см. рисунок 3.5) значение мощности на валу P2
делится на фазное напряжение U1
и количество фаз статора m1
в соответствии с выражением (2.100). Блок «Product2» делит полученное промежуточное значение на коэффициент мощности cosφ и коэффициент полезного действия η. В итоге на выходе получаем значение тока статора I1
.
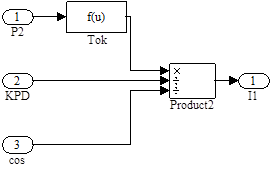
Рисунок 3.5 – Структурная схема подсистемы «Tok statora»
Подсистема «Tok rotora» (см. рисунок 3.2) рассчитывает значение тока ротора по выражению (2.106)
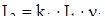 . .
Структурная схема подсистемы приведена на рисунке 3.6.

Рисунок 3.6 – Структурная схема подсистемы «Tok rotora»
Блок «Ki» (см. рисунок 3.6) представляет собой блок задания алгебраической функции, в котором рассчитывается коэффициент, учитывающий влияние тока намагничивания и сопротивления обмоток на отношение I1
/I2
, по выражению (2.107)
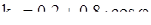 . .
В блоке «Rot» задается величина коэффициента приведения токов νi
, рассчитанного в теле m-файла по выражению (2.108)
 . .
Блок «Product3» перемножает значения тока статора I1
, коэффициента приведения токов νi
и коэффициента ki
, учитывающего влияние тока намагничивания и сопротивления обмоток на отношение I1
/I2
. В итоге на выходе имеем значение тока ротора I2
.
Подсистема «Summarnye poteri» (см. рисунок 3.2) рассчитывает суммарные потери в двигателе по выражению (2.110)
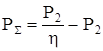 . .
Структурная схема подсистемы приведена на рисунке 3.7.
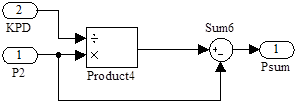
Рисунок 3.7 – Структурная схема подсистемы «Summarnye poteri»
Блок «Product4» делит значение мощности на валу двигателя P2
на коэффициент полезного действия η. На выходе «Product4» получается значение потребляемой из сети мощности P1
, из которого в сумматоре «Sum6» вычитается величина мощности на валу двигателя Р2
. В итоге на выходе подсистемы имеем значение суммарных потерь в двигателе РΣ
.
Подсистема «Dobavochnye poteri» рассчитывает величину добавочных потерь в двигателе по выражению (2.113)
 . .
Структурная схема подсистемы приведена на рисунке 3.8.

Рисунок 3.8 – Структурная схема подсистемы «Dobavochnye poteri»
Усилительный элемент «Gain3» имеет коэффициент усиления равный 0,005. Значение с выхода усилительного элемента в блоке «Product5» делится на величину коэффициента полезного действия η. В итоге на выходе подсистемы имеем значение добавочных потерь в двигателе Рдоб
.
Структурная схема для определения температуры стали приведена на рисунке 3.9. Практически все блоки идентичны блокам структурной схемы для определения температуры меди, отличие состоит в том, что в блоки передаточных функций «Cu», «Fe», «Cu(0)», «Fe(0)» и «Air» входят коэффициенты выражения (3.17).
Оценить точность полученной модели можно, сравнив результаты моделирования с данными, полученными опытным путем. Но проведение опытов является невозможным из-за отсутствия достаточной материально-технической базы, а так же из-за малого количества времени, отведенного на выполнение дипломного проекта. Приводимые в известной литературе кривые изменения температуры двигателя показывают лишь характер ее изменения и никакой точной информации не несут. Поэтому, единственным доступным в данной ситуации способом оценки достоверности результатов моделирования является сравнение их с результатами, полученными другими существующими методами тепловых расчетов. Так, например, при тепловом расчете асинхронного двигателя хакрытого исполнения мощностью Р2
=7,5 кВт с синхронной скоростью n1
=1500 об/мин в установившемся режиме по методике приведенной в [13] превышение температуры обмотки равно Δθм
=75,30
С. При расчете с помощью приведенной выше модели для того же двигателя получено значение Δθм
=73,50
С. Таким образом разница полученных значений превышения температуры обмотки статора составляет 1,80
С, то есть 2,4%, что вполне удовлетворительно.
3.3 Автоматизация расчетов параметров тепловой модели асинхронного двигателя
Расчеты коэффициентов системы дифференциальных уравнений (1.20) приведенные в разделах 3 – 6, для автоматизации вычислений реализованы с помощью системы MatLab.

Рисунок 3.9 – Схема модели определения температуры стали
Эта система позволяет обрабатывать заранее подготовленную последовательность команд и операторов, записанную в виде так называемого m-файла. Для подготовки, редактирования и отладки m-файлов служит специальный редактор-отладчик, обеспечивающий синтаксический контроль файла.
Текст m-файла, рассчитывающего необходимые для моделирования величины, приводится в Приложении А.
Следует заметить, что пакет MatLab 6.1 не поддерживает кодировку кириллицы что не позволяет использовать русскоязычные комментарии в теле m-файла [16]. В связи с этим комментарии написаны транслитерацией, то есть заменой букв кириллицы созвучными латинскими буквами. В тексте m-файла, приведенного в Приложении А, комментарии для улучшения восприятия заменены русскими.
Кротко поясним назначение основных частей программы:
1. Ввод исходных данных – в память ЭВМ вносятся все необходимые для расчета исходные данные.
2. Промежуточные вычисления – расчет промежуточных величин, которые необходимы для дальнейшего расчета. Расчет тепловых сопротивлений – здесь рассчитываются тепловые сопротивления для ЭТС закрытого обдуваемого двигателя (см. рисунок 2.2).
3. Активные сопротивления обмоток статора и ротора – расчет активных сопротивлений обмоток по формулам (2.99) и (2.102).
4. Расчет потерь – в этой части рассчитываются потери в лобовой и пазовой частях обмотки, необходимые для перехода от схемы (см рисунок 2.2) к схеме (см. рисунок 2.5), а так же константы, необходимые для определения потерь в меди и стали.
5. Расчет коэффициентов теплоотдачи – здесь производится преобразование схемы (см. рисунок 2.2) к схеме (см. рисунок 2.5), определяются тепловые проводимости, вводится замена (2.6) и по выражениям (2.15) – (2.17) определяются коэффициенты А1
, А2
и А12
.
6. Расчет теплоемкостей – рассчитываются теплоемкости меди и стали по выражениям (2.91) и (2.93).
7. Расчет коэффициентов, учитывающих вклад ротора в нагрев меди и стали – определяются весовые коэффициенты потерь в роторе, входящие в выражения (2.18) и (2.19).
8. Расчет шага интегрирования – здесь определяется оптимальный шаг интегрирования. Это необходимо потому, что используемый по умолчанию метод с переменным шагом не дает желаемого результата и приходится использовать метод с постоянным шагом (в частности метод Рунге-Кутта).
Ниже приводятся исходные данные необходимые для расчета коэффициентов системы дифференциальных уравнений на примере асинхронного двигателя марки 4А132М2У3.
Паспортные данные
3. Номинальная отдаваемая мощность P2
=11 кВт;
4. Количество фаз m1
=3;
5. Номинальное напряжение U1
н
=380 В;
6. Синхронная частота вращения n1
=3000 об/мин;
7. Количество пар полюсов p=1.
Параметры станины
9. Высота оси вращения h=132 мм;
10. Диаметр станины у основания ребер Dc
=0,245 м;
11. Длина свисающей части станины со стороны привода lсв.пр
=0,15 м;
12. Длина свисающей части станины со стороны вентилятора lсв.в
=0,15 м;
13. Зазор между диффузором и подшипниковым щитом в месте крепления δд.щ
=0;
14. Количество ребер станины zp
=12;
15. Высота ребра станины hp
=23∙10-3
м;
16. Толщина ребра станины δр
=2∙10-3
м.
Параметры вентилятора
2. Внешний диаметр вентилятора Dвент
=0,214 м.
Параметры статора
6. Внешний диаметр сердечника Da
=0,225 м;
7. Внутренний диаметр сердечника D=0,13 м;
8. Длина паза lп
=0,13 м;
9. Число пазов статора Z1
=24;
10. Коэффициент шихтовки (заполнения пакета сталью) kш
=0,97.
Параметры паза статора
9. Большая ширина паза b1
=13,4∙10-3
м;
10. Меньшая ширина паза b2
=10,2∙10-3
м;
11. Высота паза hп
=16,5∙10-3
м;
12. Коэффициент заполнения паза kз
=0,75;
13. Высота шлица hш
=0,9∙10-3
м;
14. Ширина шлица bш
=4∙10-3
м;
15. Высота зубца hз
=16,5∙10-3
м;
16. Ширина зубца bз
=6,56∙10-3
м.
Параметры ротора
10. Внешний диаметр ротора Dрот
=129∙10-3
м;
11. Число пазов ротора Zрот
=19;
12. Ширина короткозамыкающего кольца bк
=25∙10-3
м;
13. Высота короткозамыкающего кольца aк
=23∙10-3
м;
14. Ширина лопатки ротора bл
=41∙10-3
м;
15. Высота лопатки ротора ал
=22∙10-3
м;
16. Количество лопаток ротора zл
=12;
17. Коэффициент качества лопатки, рассматриваемой как ребро ηл
=0,6;
18. Толщина воздушного зазора между ротором и статором δ=0,6∙10-3
м.
Параметры паза ротора
1. Ширина паза у вершины b1р
=10,8∙10-3
м;
2. Ширина паза у основания b2р
=7,1∙10-3
м;
3. Высота паза ротора hпр
=20,2∙10-3
м.
Параметры обмотки
8. Количество витков в обмотке фазы ω1
=84;
9. Число параллельных ветвей а=1;
10. Число элементарных проводников в эффективном n=3;
11. Средняя длина витка обмотки lср1
=0,722 м;
12. Развернутая длина лобовой части обмотки с одной стороны lл
=0,256 м;
13. Длина вылета лобовой части обмотки с одной стороны lл.в
=70∙10-3
м;
14. Диаметр изолированного проводника dи
=1,28 мм;
15. Коэффициент пропитки обмотки kп
=0,9;
16. Обмоточный коэффициент kобм
=0,958;
17. Толщина окраски обмотки в лобовой части δокр
=0 м;
Параметры пазовой изоляции
2. Толщина пазовой изоляции δи.п
=0,25∙10-3
м.
Общие физические величины
11. Кинематическая вязкость воздуха ν=15,8∙10-6
м2
/с;
12. Коэффициент теплопроводности воздуха λв
=0,03 Вт/(о
С∙м);
13. Средняя температура обмотки Tср
=100 о
С;
14. Коэффициент теплопроводности меди обмотки λм
=384 Вт/(о
С∙м);
15. Коэффициент теплопроводности алюминия клетки λа
=189 Вт/(о
С∙м);
16. Коэффициент теплопроводности материала станины λст
=160 Вт/(о
С∙м);
17. Коэффициент теплопроводности стали пакета статора λс
=34 Вт/(о
С∙м);
18. Коэффициент теплопроводности пропиточного состава обмотки λп
=0,28 Вт/(о
С∙м);
19. Коэффициент теплопроводности изоляции проводов λи
=0,26 Вт/(о
С∙м);
20. Коэффициент теплопроводности окраски обмотки в лобовой части λокр
=0,2 Вт/(о
С∙м);
21. Коэффициент теплопроводности пазовой изоляции λи.п
=0,41 Вт/(о
С∙м);
22. Плотность меди γм
=8,89∙103
кг/м3
;
23. Плотность стали γст
=7,65∙103
кг/м3
;
24. Удельная теплоемкость меди см
=386 Дж/(кг∙К);
25. Удельная теплоемкость стали сст
=500 Дж/(кг∙К).
В результате расчета в MatLab 6.1 получены следующие результаты:
1. Коэффициент теплоотдачи от меди к окружающему воздуху А1
=0,5046 Вт/0
С.
2. Коэффициент теплоотдачи от стали к окружающему воздуху А2
=46,7726 Вт/0
С.
3. Коэффициент теплоотдачи от меди к стали А12
=9,7796 Вт/0
С.
4. Теплоемкость меди С1
=2577,1 Дж/0
С.
5. Теплоемкость стали С2
=1036,6 Дж/0
С.
Так как цель данного дипломного проекта – это создание лабораторной работы, поэтому в Приложении Б приведены исходные данные к расчету еще для четырех двигателей серии 4А: 4А180М2У3, 4А132М4У3, 4А180М4У3, 4А225М4У3.
4. Моделирование процессов нагрева и охлаждения асинхронного двигателя в различных режимах работы. Рекомендации по выбору асинхронных двигателей по нагреву
Исследуем стандартные режимы работы асинхронных двигателей, установленные ГОСТ 183–74: S1, S2, S3.
Режим S1 – это режим продолжительной работы при постоянной нагрузке.
Режим S2 – режим кратковременной нагрузки. Двигатель в режиме S2 работает при постоянной нагрузке в течение времени меньшего, чем требуется для получения теплового равновесия, с последующим отключением на время, за которое температура двигателя становится равной температуре окружающей среды. Характеризуемой величиной в этом режиме служит продолжительность работы. Стандартные значения, установленные ГОСТ 183–74: 10, 30, 60, 90 минут.
Режим S3 – режим повторно-кратковременной нагрузки. Характеризуется последовательностью идентичных циклов, каждый из которых состоит из периодов работы двигателя при постоянной нагрузке и периодов отключения, причем длительность периодов работы недостаточна для достижения теплового равновесия за время одного рабочего цикла. Этот режим характеризуется продолжительностью включения (ПВ), которая равна:
 , (4.1) , (4.1)
где tp
– время работы;
tо
– время отключения.
В ГОСТ 183–74 устанавливаются стандартные значения ПВ: 15%, 25%, 40%, 60%. Продолжительность одного цикла, если не оговорок, принимается равной десяти минутам.
Рассмотрим процессы нагрева на примере асинхронного двигателя закрытого исполнения марки 4А132М2У3. При моделировании температура окружающего воздуха принималась равной 100
С, начальные температуры меди и стали равны температуре окружающего воздуха. По графику видно, что средняя температура меди достигает установившегося значения 82,730
С за 2000 секунд.

Рисунок 4.1 – График изменения нагрузки и температур меди и стали в режиме S1 (θв
=100
С)
Графики изменения нагрузки и температур меди и стали в режиме S2 приведены на рисунке 4.2. Продолжительность работы здесь равна 10 минутам, температура окружающей среды и начальные температуры меди и стали равны 100
С.

Рисунок 4.2 – Графики изменения нагрузки и температур меди и стали в режиме S2 (θв
=100
С)
По графику видно, что средняя температура меди не достигает установившегося состояния, ее максимум равен 72,30
С. После отключения обмотка остывает до температуры окружающей среды, то есть до 100
С, за 1800 секунд.
Графики изменения нагрузки и температур меди и стали в режиме S3 приведены на рисунке 4.3.
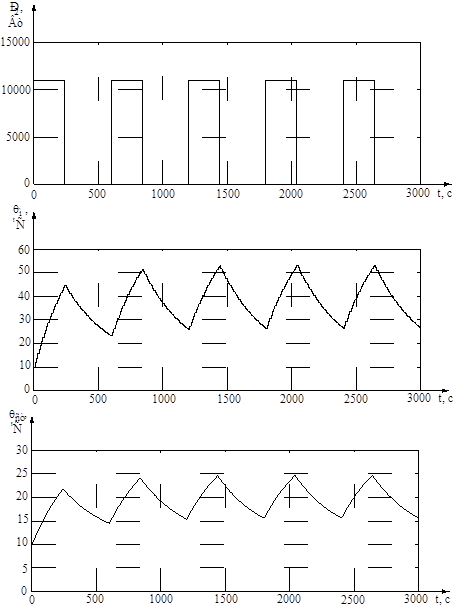
Рисунок 4.3 – Графики изменения нагрузки и температур меди и стали в режиме S3 (θв
=100
С)
Продолжительность включения ПВ=40%, температура окружающей среды и начальные температуры меди и стали равны 100
С. По графику видно, что средняя температура меди не достигает установившегося состояния, ее максимум равен 53,20
С. Установившееся состояние наступает через три цикла.
На рисунках 4.4–4.6 приведены графики изменения нагрузки и температур меди и стали в режимах S1, S2 и S3 соответственно, при температуре окружающего воздуха 400
С. Начальные температуры меди и стали равны температуре окружающего воздуха.

Рисунок 4.4 – Графики изменения нагрузки и температур меди и стали в режиме S1 (θв
=400
С)
По графику изменения температуры меди в режиме S1 (см. рисунок 4.4) видно, что установившееся значение температуры равно 1130
С. Это значение меньше установленного ГОСТ 183–74 предельное значение температуры для изоляции класса В – 1200
С.

Рисунок 4.5 – Графики изменения нагрузки и температур меди и стали в режиме S2 (θв
=400
С)

Рисунок 4.6 – Графики изменения нагрузки и температур меди и стали в режиме S3 (θв
=400
С)
При проектировании электропривода встает задача выбора асинхронного двигателя по мощности. Если мощность, требуемая на исполнительном органе рабочего механизма, больше чем мощность двигателя, то последний перегревается и может выйти из строя; если мощность нагрузки меньше мощности двигателя, то ухудшаются его энергетические характеристики (коэффициент полезного действия η, коэффициент мощности cosφ). Задача выбора двигателя осложняется тем, что нагрузка на валу не остается постоянной, а меняется во времени. Для того чтобы решить вопрос выбора мощности двигателя, необходимо знать зависимость изменения нагрузки во времени.
Таким образом, основной целью при выборе асинхронного двигателя по нагреву является наиболее полное его использование по мощности.
Предельные значения температур обмоток для разных классов изоляции устанавливаются ГОСТ 183–74. Предельные температуры обмотки для классов пазовой изоляции приведены в таблице 4.1.
Таблица 4.1
| Класс нагревостойкости изоляции
|
B
|
F
|
H
|
| Предельно допускаемые температуры обмоток
машин, 0
С
|
120
|
140
|
165
|
| Предельно допускаемые превышения температуры обмоток машин, 0
С
|
80
|
100
|
125
|
При работе привода в режиме продолжительной работы с постоянной нагрузкой (S1) перегрузка двигателя недопустима, то есть мощность нагрузки должна быть меньше либо равна установленной мощности двигателя. Причиной этого является то, что при номинальной нагрузке температура меди обмотки близка к предельно допустимой.
При работе привода в кратковременном режиме с постоянной нагрузкой (S2) имеется возможность получить от двигателя мощность больше паспортной. Это объясняется тем, что в кратковременном режиме работы температура обмотки не достигает установившегося значения, а при отключении от сети двигатель остывает до температуры окружающей среды. Величина допустимой перегрузки в первую очередь зависит от продолжительности работы двигателя.
При работе электропривода в повторно-кратковременном режиме (S3), температура обмотки в течение одного цикла не достигает установившегося значения, а при отключении двигателя от сети, он не успевает остыть до температуры окружающей среды. Поэтому в этом режиме, так же как и в режиме S2, возможна некоторая перегрузка двигателя. Величина допустимой перегрузки определяется продолжительностью включения, а именно временем работы и временем отключения.
На практике режимы работы электропривода отличаются от стандартизированных режимов. В этом случае, зная характер изменения нагрузки, можно смоделировать соответствующий режим на ЭВМ и определить температуру двигателя в конкретном режиме работы.
Однако следует учитывать, что ни одна, даже самая сложная модель асинхронного двигателя не обеспечивает точное решение задачи. Это объясняется, во-первых, приближенностью определения коэффициентов системы дифференциальных уравнений через конструктивные параметры асинхронного двигателя, и, во-вторых, технологическим разбросом характеристик самого двигателя. Так, например, только разброс характеристик материалов, применяемых при изготовлении асинхронных двигателей, может достигать ±18% [2].
Поэтому известные попытки использования устройств защиты асинхронных двигателей, реализованных с помощью тепловых моделей [9,11,12], по мнению автора, не способны обеспечить срабатывание защиты именно в тот момент времени, когда фактическая температура обмотки достигает значения уставки. В публикациях, посвященных этим устройствам защиты, отсутствует оценка погрешности их срабатывания.
Однако для решения задачи выбора двигателя по мощности тепловую модель использовать можно, так как при проектировании электропривода мощность двигателя выбирается с небольшим запасом, который компенсирует погрешность модели.
5. Экономический расчет
Затраты на разработку и реализацию лабораторной работы определяются по формуле:
 , (5.1) , (5.1)
где Сосн,зп
– основная заработная плата персонала, руб.;
Сдоп,зп
– дополнительная заработная плата персонала, руб.;
Сн,з
– налоги на заработную плату, руб.;
Спо
– затраты на приобретение программного обеспечения, руб.;
Свт
– затраты на содержание и эксплуатацию вычислительной техники, руб.;
Сн
– накладные расходы, руб.
Основная заработная плата рассчитывается как:
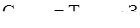 , (5.2) , (5.2)
где Тразраб
– время необходимое для разработки лабораторной работы, ч;
З – основная заработная плата персонала за один час, руб./ч.
Для разработки лабораторной работы необходимо Тразраб
=150 ч. Исполнителем является инженер-программист. Оклад инженера-программиста третьей категории составляет 800 руб. в месяц. При условии, что продолжительность рабочего дня равна 8 ч, а в месяце 22 рабочих дня, основная заработная плата за 1 ч составит:
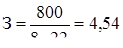 руб./ч. руб./ч.
Основная заработная плата инженера-программиста за весь период разработки в соответствии с выражением (5.2) составит:
 руб. руб.
Дополнительная заработная плата рассчитывается в процентах от основной заработной платы и составляет 12%. Дополнительная заработная плата инженера-программиста за весь период разработки составит:
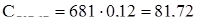 руб. руб.
Налоги на заработную плату берутся в размере 36,6% от суммы основной и дополнительной заработной платы. Налоги на заработную плату за весь период разработки и реализации лабораторной работы составят:
 руб. руб.
Затраты на приобретение программного обеспечения берутся как стоимость программного обеспечения. Стоимость полного пакета MatLab 6.1, в которой реализуется лабораторная работа, 52500 руб. Следовательно затраты на приобретение программного обеспечения составят:
Спо
=52500 руб.
Затраты на содержание и эксплуатацию вычислительного комплекса определяются следующим образом:
 , (5.3) , (5.3)
где см-ч
– стоимость машино-часа, руб./ч.
Стоимость машино-часа:
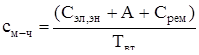 , (5.4) , (5.4)
где Сэл,эн
– стоимость потребляемой в год электроэнергии, руб.;
А – амортизация в год, руб.;
Срем
– затраты на ремонт в год, руб.;
Твт
– действительный фонд времени работы вычислительной техники, ч.
Стоимость потребляемой в год электроэнергии:
 , (5.5) , (5.5)
где р – мощность, потребляемая из сети одной ЭВМ, кВт;
Тном
– номинальный фонд времени работы ЭВМ в год, ч;
сэ
– стоимость 1 кВт/ч электрической энергии, руб./(кВт∙ч).
Мощность, потребляемая из сети одной ЭВМ, р=0,25 кВт. Стоимость 1 кВт∙ч электрической энергии сэ
=1,2 руб./(кВт∙ч). При условии, что продолжительность рабочего дня равна 8 ч, а в месяце 22 рабочих дня, номинальный фонд времени работы ЭВМ равен:
Tном
=8∙22∙12=2112 ч.
За год отчисления на электрическую энергию составят:
 руб. руб.
Амортизация вычислительной техники считается как 25% от ее балансовой стоимости. Стоимость ЭВМ, необходимой для работы – 15000 руб. Амортизация вычислительной техники за год составит:
 руб. руб.
Затраты на ремонт в год считаются как 4% от стоимости ЭВМ и составляют:
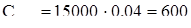 руб. руб.
Действительный фонд времени работы ЭВМ в год рассчитывается как:
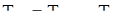 , (5.6) , (5.6)
где Тном
– номинальный годовой фонд времени работы ЭВМ, ч;
Тпроф
– годовые затраты времени на профилактические работы (принимаются 10% от Тном
), ч.
Действительный фонд времени работы ЭВМ по выражению (5.6):
 ч. ч.
Стоимость машино-часа по выражению (12.4):
 руб./ч. руб./ч.
Затраты на содержание и эксплуатацию ЭВМ по выражению (5.3):
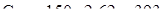 руб. руб.
Накладные расходы рассчитываются как 30% от основной заработной платы и составляют:
 руб. руб.
Смета затрат на разработку и реализацию лабораторной работы приведена в таблице 5.1.
Таблица 5.1 – Смета затрат на разработку и реализацию лабораторной работы
| № п/п
|
Наименование статьи расхода
|
Цена за единицу, руб.
|
Кол-во
|
Стоимость, руб.
|
| 1
|
Основная заработная плата персонала.
|
–
|
–
|
681
|
| 2
|
Дополнительная заработная плата персонала.
|
–
|
12%
|
81,72
|
| 3
|
Налоги на заработную плату
|
–
|
36,6%
|
279,16
|
| 4
|
Программное обеспечение.
|
52500
|
1
|
52500
|
| 5
|
Содержание и эксплуатация вычислительной техники.
|
393
|
1
|
393
|
| 6
|
Накладные расходы.
|
–
|
30%
|
204,3
|
| ИТОГО:
|
54139,18
|
Заключение
В процессе дипломирования была решена задача определения параметров тепловой модели асинхронного двигателя. В основе последней лежит представление двигателя двумя коаксиальными цилиндрами. Внешний цилиндр представляет сталь сердечника статора, внутренний – медь обмоток статора. Процессы нагрева и охлаждения в двигателе в этом случае описываются системой дифференциальных уравнений второго порядка. Коэффициенты теплоотдачи входящие в эту систему были определены путем преобразования эквивалентной тепловой схемы асинхронного двигателя закрытого исполнения, содержащей шесть узлов, в схему с двумя узлами. Преобразование тепловой схемы выполнялось для стационарного режима, так как коэффициенты теплоотдачи в переходном и стационарном режимах одинаковы.
Полученные результаты используются в компьютерной лабораторной работе «Моделирование нагрева асинхронного двигателя в различных режимах работы». Лабораторная работа выполнена в программной среде MatLab 6.1, и в ее приложении Simulink 4. Данная работа позволяет моделировать процессы нагрева и охлаждения асинхронного двигателя практически в любых режимах его работы. Изначально для моделирования предлагаются три основных режима работы асинхронного двигателя – S1, S2, S3, но так же имеется возможность задания произвольного режима работы средствами приложения Simulink.
Список использованных источников
1. Алекссев А.Е. Конструкция электрических машин. – М.: ГЭИ, 1949. – 562 с.
2. Борисенко А.И., Костиков А.И., Яковлев А.И. Охлаждение промышленных электрических машин. – М.: Энергоатомиздат, 1983. – 296 с.
3. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. – М.: Энергоатомиздат, 1981. – 346 с.
4. Сипайлов Г.А., Санников Д.И., Жадан В.А. Тепловые, гидравлические и аэродинамические расчеты в электрических машинах. – М.: Высш. шк., 1989. – 239 с.
5. Филиппов И.Ф. Теплообмен в электрических машинах. – Л.: Энергоатомиздат, 1986. – 256 с.
6. Ковалев В.З. Моделирование электротехнических комплексов и систем как совокупности взаимодействующих подсистем различной физической природы: Дисс. д-ра техн. наук: 05.09.03/ОмГТУ. – Омск, 2000. – 338 с.
7. Ключев В.И. Теория электропривода. – М.: Энергоатомиздат, 1985. – 560 с.
8. Михайлов О.П. Автоматизированный электропривод станков и промышленных роботов. – М.: Машиностроение, 1990. – 238 с.
9. Беспалов В.Я., Мощинский Ю.А., Цуканов В.И. Упрощенная математическая модель нестационарного нагрева и охлаждения обмотки статора асинхронного двигателя. // Электричество. – 2003. – №4. – С. 20–26.
10. Герман-Галкин С.Г. Компьютерное моделирование полупроводниковых систем в MatLab 6.0. – СПб.: Корона принт, 2001. – 320 с.
11. Синчук О.Н., Чумак В.В., Михайлов С.Л. Тепловая модель кранового АД для диагностирования и настройки цифровой защиты от перегрузок. // Электротехника. – 2003. – №3. – С. 61–65.
12. Бугаев Г.А., Леонтьев А.Н., Ерохин Е.Ю., Павлова Д.А. Математические модели нагрева и охлаждения асинхронных двигателей для микропроцессорного реле тепловой защиты. // Электротехника. – 2001. – №2. – С. 31–36.
13. Гольдберг О.Д., Гурин Я.С., Свириденко И.С. Проектирование электрических машин. – М.: Высш. шк., 1984. – 431 с.
14. Копылов И.П. Электрические машины. – М.: Высш. шк., 2000. – 607 с.
15. Домбровский В.В., Зайчик В.М. Асинхронные машины: Теория, расчет, элементы проектирования. – Л.: Энергоатомиздат, 1990. – 368 с.
16. Дьяконов В.П. MatLab 6/6.1/6.5+Simulink 4/5. Основы применения. Полное руководство пользователя. – М.: СОЛОН-Пресс, 2002. – 768 с.
17. Асинхронные двигатели серии 4А: Справочник/А.Э. Кравчик и др. – М.: Энергоатомиздат, 1982. – 504 с.
Приложение А
Текст m-файла, рассчитывающего параметры тепловой модели
%–1. Исходные данные–%
% Основные параметры
P2=11000;%Номинальная мощность на валу двигателя
KPD=[eps 0.8 0.87 0.88 0.88 0.87];%Коэффициент полезного действия
cosf=[eps 0.65 0.82 0.87 0.9 0.9];%Коэффициент мощности
U1_lin=380;%Номинальное линейное напряжение
n1=3000;%Синхронная частота вращения
m=3;%Количество фаз статора
h=132;%Высота оси вращения, мм
p=1;%Число пар полюсов
% Параметры станины
Dc=0.245;%Диаметр станины у основания ребер
l_svp=0.15;%Длина свисающей части станины со стороны привода
l_svv=0.15;% Длина свисающей части станины со стороны вентилятора
d_dsh=0;%Зазор между диффузором и щитом в месте крепления
Z_rs=12;%Количество ребер станины
h_rs=23*10^(-3);%Высота ребра станины
d_rs=0.002;%Толщина ребра станины
% Параметры вентилятора
D_v=0.214;%Внешний диаметр вентилятора
% Параметры статора
Da=0.225;%Внешний диаметр сердечника
D=0.13;%Внутренний диаметр сердечника
l_p=0.13;%Длина паза
Z1=24;%Число пазов статора
kc=0.97;%Коэффициент шихтовки
%Параметры паза статора
b1=0.0134;%Ширина паза статора у основания
b2=0.0102;%Ширина паза статора в вершине
h_p=0.0165;%Высота паза
k_zp=0.75;% Коэффициент заполнения паза
h_sh=0.0009;%Высота шлица
b_sh=0.004;%Ширина шлица
b_z=0.00656;%Ширина зубца
h_z=0.0165;%Высота зубца
%Параметры ротора
D_rot=0.129;%Внешний диаметр ротора
Z2=19;%Число пазов ротора
b_k=0.025;%Ширина короткозамыкающего кольца
a_k=0.023;%Высота короткозамыкающего кольца
b_l=0.041;%Ширина лопатки ротора
a_l=0.022;%Высота лопатки ротора
n_l=12;%Количество лопаток ротора
KPD_lr=0.6;%Коэффициент качества лопатки, рассматриваемой как ребро
d=0.6*10^(-3);%Толщина воздушного зазора между ротором и статором
%Параметры паза ротора
b1_rot=10.8*10^(-3);%Ширина паза ротора в вершине
b2_rot=7.1*10^(-3);%Ширина паза ротора у основания
h_p_rot=20.2*10^(-3);%Высота паза ротора
% Параметры обмотки статора
w_1=84;%Число витков в фазе обмотки
a=1;%Число параллельных ветвей в фазе обмотки статора
n=3;%Число элементарных проводников в эффективном
l_sr=0.772;%Средняя длина витка обмотки статора
l_lob=0.256;%Развернутая длина лобовой части с одной стороны
l_lobv=0.07;%Длина вылета лобовой части
d_i=1.28;%Диаметр изолированного элементарного проводника обмотки
k_p=0.9;%Коэффициент пропитки обмотки статора
k_obm=0.958;%Обмоточный коэффициент обмотки статора
d_okr=0;%Толщина окраски обмотки в лобовой части
T_sr=100;%Средняя температура обмотки, град
% Параметры изоляции
d_ip=0.25*10^(-3);%Толщина пазовой изоляции
% Коэффициенты, характеризующие физические свойства материалов
v=15.8*10^(-6);%Кинематическая вязкость воздуха
lam_v=0.03;%Коэффициент теплопроводности воздуха
lam_m=384;%Коэффициент теплопроводности меди
lam_a=189;%Коэффициент теплопроводности алюминия клетки
lam_st=47;% Коэффициент теплопроводности материала станины
lam_s=34;% Коэффициент теплопроводности стали пакета статора
lam_p=0.28;% Коэффициент теплопроводности пропиточного состава
lam_i=0.26;% Коэффициент теплопроводности изоляции проводов
lam_okr=0.2;%Коэффициент теплопроводности окраски обмотки в лобовой части
lam_p_iz=0.41;% Коэффициент теплопроводности пазовой изоляции
gamma_m=8.89*(10^3);%Плотность меди обмотки статора
gamma_st=7.65*(10^3);%Плотность стали пакета статора
c_m=386;%Удельная теплоемкость меди обмотки статора
c_st=500;%Удельная теплоемкость стали пакета статора
r_m=(1/57)*(10^(-6));%Удельное сопротивление меди обмотки статора
r_al=(1/22)*(10^(-6));%Удельное сопротивление алюминия клетки ротора
%–2. Промежуточные вычисления–%
%Окружная скорость ротора
u=(pi*n1*D_rot)/60;
% Окружная скорость вентилятора
u_vent=(pi*n1*D_v)/60;
%Эффективная (по меди) ширина паза
b_p_ef=((b1+b2)/2) – 2*d_ip;
%Эффективная (по меди) высота паза
h_p_ef=h_p-2*d_ip-h_sh – ((b2-b_sh)/2);
%Средняя ширина паза
b_p=(b1+b2)/2;
%Внутренний диаметр лобовой части
D_l_vt=D+h_sh+d_ip+(b2-b_sh)/2;
%Внешний диаметр лобовой части
D_l_vsh=D_l_vt+1.4*h_p_ef;
%Диаметр окружности касательной к дну пазов
D_dp=D+2*h_p;
%Эквивалентный коэффициент теплопроводности обмотки
lam_ekv=exp (-4*k_zp)*(4.65*(k_zp^1.5) – 0.7053)*(1+0.81*(d_i^2)-…
0.32*d_i*(1–9.2*k_p+5.2*(k_p^2)))*…
(1+(0.0428*k_zp0.0253)*T_sr)*((lam_p/0.162)^0.33)*((lam_i/0.143)^0.25);
%Эквивалентный коэффициент теплопроводности воздушных прослоек в пазу
lam_v_ekv=2*lam_v*lam_p*(lam_p*k_p+lam_v*(1 – k_p))/(lam_v*lam_p+…
(lam_p*k_p+lam_v*(1-k_p))*(lam_v*k_p+lam_p*(1-k_p)));
%Термическое сопротивление зубца
R_z=h_z/(3*lam_s*b_z*l_p*Z1*kc);
%Площадь меди в пазу статора
F_m=(3*a*w_1*pi*(d_i^2)/(2*Z1))*10^(-6);
%Площадь алюминия в пазу ротора
F_a=(pi/8)*((b1_rot^2)+(b2_rot^2))+(h_p_rot/2)*(b1_rot+b2_rot);
%Выбор толщины воздушных прослоек
if 50<=h<=132
d_vp=0.05*(10^(-3));
elseif 160<=h<=250
d_vp=0.1*(10^(-3));
else
d_vp=0.15*(10^(-3));
end
%–3. Расчет тепловых сопротивлений–%
%–3.1 Сопротивление аксиальное меди статора–%
R_a=(l_p+l_lob)/(12*lam_m*F_m*Z1);
disp ('Сопротивление аксиальное меди статора'); disp (R_a);
%–3.2 Сопротивление между внутренним воздухом и корпусом–%
%Площадь внутренней поверхности свесов станины
F_st_pr=(Da*pi*l_svp)/2;
F_st_v=(Da*pi*l_svv)/2;
%Площадь поверхности подшипникового щита
F_sch=(Da^2)*pi/4;
%Коэффициент теплопередачи внутренней поверхности свесов станины
RE_s=(u*Da)/(2*v);
if h<160
NU_s=43.78*(RE_s^0.17)*((Da-D_l_vsh)/D)^0.25;
else
if d_dsh==0
NU_s=11.64*(RE_s^0.395);
else
NU_s=3*(RE_s^0.495)/ln (1.3*D/(Da-D));
end
end
a_s=NU_s*lam_v/Da;
%Сопротивление между внутренним воздухом и открытыми частями станины
R_st_pr=1/(F_st_pr*a_s);
R_st_v=1/(F_st_v*a_s);
%Коэффициент теплоотдачи внутренней поверхности подшипникового щита
RE_sch=u*(Da+D)/(4*v);
if h<160
NU_sch=8.34*(RE_sch^0.26)*((Da-D)/D)^(-0.5);
else
if d_dsh==0
NU_shs=5.12*(RE_sch^0.48)*(2*Da/(Da+D))^(-0.52);
else
NU_sch=1.01*(RE_sch^0.63)*ln (D/(5.25*d_dsh))*(2*Da/(Da+D))^(-0.52);
end
end
a_sch=(2*NU_sch*lam_v)/(Da+D);
%Сопротивление между внутренним воздухом и подшипниковым щитом
R_sch=1/(F_sch*a_sch);
%Сопротивление между внутренним воздухом и корпусом
R_vk=1/((1/R_st_pr)+(1/R_st_v)+(2/R_sch));
disp ('Сопротивление между внутренним воздухом и корпусом'); disp (R_vk);
%–3.3 Сопротивление между внешним воздухом и корпусом–%
%Расходная скорость на входе в каналы
w_vh=0.45*u_vent;
%Эффективная скорость
w_ef=sqrt((w_vh^2)+0.25*(u_vent^2));
%Шаг ребер
t_r=2*Dc*pi/(2*Z_rs);
%Гидравлический диаметр межреберного канала
d_g=4*h_rs*t_r/(2*h_rs+t_r);
%Коэффициент теплопроводности на входе в канал
RE_ef=w_ef*d_g/v;
NU_vh=0.627*(RE_ef^0.52);
a_vh=NU_vh*lam_v/d_g;
%Коэффициент уменьшения КТО
gamma=0.055*(1-tanh (0.062*((Dc/d_g) – 12.5)));
%Коэффициент теплоотдачи станины над пакетом
a_sp=a_vh*d_g*(1-exp (-gamma*l_p/d_g))/(gamma*l_p);
%Коэффициент теплоотдачи свисающей части станины со стороны привода
a_spr=a_vh*d_g*(1-exp (-gamma*l_svp/d_g))/(gamma*l_svp);
%Коэффициент теплоотдачи свисающей части станины со стороны вентилятора
a_sv=a_vh*d_g*(1-exp (-gamma*l_svv/d_g))/(gamma*l_svv);
%Коэффициент качества ребер станины
mh=h_rs*sqrt (2*a_sp/(d_rs*lam_st));
KPD_r=tanh(mh)/mh;
%Сопротивление между станиной над пакетом и внешним воздухом
R7=1/(a_sp*l_p*(pi*Dc-Z_rs*d_rs+2*h_rs*Z_rs*KPD_r));
%Сопротивление между свисающей частью станины со стороны привода и внешним воздухом
R6=1/(a_spr*l_svp*(pi*Dc-Z_rs*d_rs+2*h_rs*Z_rs*KPD_r));
%Сопротивление между свисающей частью станины со стороны вентилятора и внешним воздухом
R8=1/(a_sv*l_svv*(pi*Dc-Z_rs*d_rs+2*h_rs*Z_rs*KPD_r));
%Коэффициент теплоотдачи внешней поверхности подшипникового щита со стороны привода
a_sch_pr=20+1.6*(u_vent^0.7);
%Коэффициент теплоотдачи внешней поверхности подшипникового щита со стороны вентилятора
if h<160
a_sch_v=20+8.2*(u_vent^0.8);
else
a_sch_v=20+9.4*(u_vent^0.6);
end;
%Площадь поверхности подшипникового щита
F_sch=(Da^2)*pi/4;
%Сопротивление подшипникового щита со стороны привода
R26=1/(a_sch_pr*F_sch);
%Сопротивление подшипникового щита со стороны вентилятора
R11=1/(a_sch_v*F_sch);
%Сопротивление между внешним воздухом и корпусом
R_k=1/((1/R6)+(1/R7)+(1/R8)+(1/R11)+(1/R26));
disp ('Сопротивление между внешним воздухом и корпусом'); disp (R_k);
%–3.4 Сопротивление между медью статора и внутренним воздухом–%
%Продуваемая длина лобовой части обмотки с одной стороны
l_lobp=l_lobv-1.4*b_p;
%Коэффициенты теплоотдачи лобовых частей обмоток статора
RE_vsh=u*D_l_vsh/(2*v);
RE_vt=u*D_l_vt/(2*v);
NU_vsh=0.103*(RE_vsh^0.67);
NU_vt=0.456*(RE_vt^0.6);
a_l_vsh=NU_vsh*lam_v/D_l_vsh;
a_l_vt=NU_vt*lam_v/D_l_vt;
%Сопротивление внешней продуваемой лобовой части обмотки
R1_l_vsh=(0.104*b_p*h_p_ef/(lam_ekv*l_lobp*Z1*((b_p^2)+0.25*…
(h_p_ef^2))))+(0.75*((d_okr/lam_okr)+(1/a_l_vsh))/(l_lobp*Z1*(b_p+…
0.5*h_p_ef)));
%Сопротивление внешней непродуваемой лобовой части обмотки
R2_l_vsh=((h_p_ef/(3*lam_ekv))+(d_okr/lam_okr)+(1/a_l_vsh))/…
(pi*D_l_vsh*(l_lobv-l_lobp));
%Сопротивление внутренней продуваемой лобовой части обмотки
R1_l_vt=(0.104*b_p*h_p_ef/(lam_ekv*l_lobp*Z1*((b_p^2)+0.25*…
(h_p_ef^2))))+(0.75*((d_okr/lam_okr)+(1/a_l_vt))/(l_lobp*Z1*(b_p+…
0.5*h_p_ef)));
%Сопротивление внутренней непродуваемой лобовой части обмотки
R2_l_vt=((h_p_ef/(3*lam_ekv))+(d_okr/lam_okr)+(1/a_l_vt))/…
(pi*D_l_vt*(l_lobv-l_lobp));
%Сопротивление между медью и внутренним воздухом
R_m_v=1/((1/R1_l_vsh)+(1/R2_l_vsh)+(1/R1_l_vt)+(1/R2_l_vt));
disp ('Сопротивление между медью статора и внутренним
воздухом'); disp (R_m_v);
%–3.5 Сопротивление между медью и сердечником статора–%
%Сопротивление отводу теплоты через дно паза
R20=((h_p_ef/(3*lam_ekv))+(d_ip/lam_p_iz)+(d_vp/lam_v_ekv))/…
(b_p_ef*l_p*Z1);
%Внутреннее сопротивление обмотки
R_vn=b_p_ef/(12*lam_ekv*h_p_ef*l_p*Z1);
%Сопротивление пазовой изоляции
R_ip=(d_ip/lam_p_iz)/(2*h_p_ef*l_p*Z1);
%Сопротивление воздушных прослоек
R_vp=d_vp/(2*lam_v_ekv*h_p_ef*l_p*Z1);
%Сопротивление между пазовой частью обмотки и зубцами
R17=R_vn+R_ip+R_vp;
%Сопротивление, учитывающее разное сопротивление спинки серднчника собственному и внешнему тепловым потокам
|