№1. Трубопровод диаметром dдлиной l = 150 м, подготовленный к гидравлическому испытанию, заполнен водой при атмосферном давлении. Какое количество воды необходимо дополнительно подать в трубопровод, чтобы давление в нем поднялось до значения рн
по манометру?
Модуль упругости воды Е= 2,0 ГПа.
Дано:
d=150 мм
PН
=4,0 мПа
l=150 м
E=2,0 гПа
|
| ∆W-? |
Решение:
1. Модуль объёмной упругости жидкости равен:
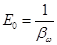 , ,
где 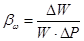 - коэффициент объёмного сжатия. - коэффициент объёмного сжатия.
2. Отсюда получаем:
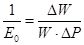 , ,
где 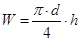 - первичный объём, - первичный объём,  -изменение объёма при изменении давления на величину -изменение объёма при изменении давления на величину 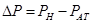 ( (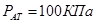 -атмосферное давление). -атмосферное давление).
3. Следовательно, необходимое количество воды будет находиться по формуле:

Ответ: 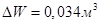
№ 2. Закрытый резервуар с нефтью снабжен ртутным и механическим манометрами. Определить показание РМ
(см. рис. 1) механического манометра, если глубина подключения ртутного манометра Н=1,5 м, известны размеры h и а. Плотность нефти ρ=860 кг/м3
.
Дано:
H (hН
) =1,5 м
h=4 м
а (h3
)=6 м
ρН
=860 кг/м3
РМ
=?
Решение:
Плотность ртути = 13595кг/м3
;
давление атмосферы: РАТ
=9,81.
104
Па.
Т. к. РМ
> РАТ,
то РМ
+rН
ghН
=РАТ
+rР
gh - rН
gh3
,
где h=4м, hН
=1,5м, h3
=6м.
Тогда РМ=
РАТ
+ rР
gh - rН
gh3
- rН
ghН
=9,81.
104
+13595.
9,81.
4 - 860.
9,81.
6 -
860.
9,81.
1,5 = 9,81.
104
+ 533467,8 - 50619,6 - 12654,9 = 568293,3 = 568,293 кПа.
Ответ: РМ
= 568,293 кПа.
№3. Определить высоту h1
(см. рис. 2), на которую может поднять воду прямодействующий паровой поршневой насос, если манометрическое давление в паровом цилиндре рм
= 500 кПа.
Дано:
рм
= 500 кПа
d=0,25м
D=0,35м
h1
=?
Решение:
р=F/S,
где р – давление, F – сила действующая на площадь S.
Таким образом
F=рS.
Т. к. сила действующая на поршень 1 и на поршень 2 одинакова, то составим уравнение:
S1
p1
=S2
gв
h1
,
где S1
и S2
– площадь поршней насоса и цилиндра соответственно,
gв
– удельный вес воды равный 9,789 кН/м3
,
h1
– высота подъёма жидкости.
S=pd2
/4, где в – диаметр круга,
S1
=3,14.
0,252
/4=0,049 м2
,
S2
=3,14.
0,352
/4=0,096 м2
Получаем:
h1
=(0,049.
500000)/(0,096.
9789)=24500/939,744=26,07 м.
Ответ: h1
=26,07 м.
№4. Определить абсолютное и вакуумметрическое давление в сосуде А, заполненном воздухом, если показание вакуумметра hв
= 30см, а относительная плотность жидкости ρ=0,9∙103
кг/м3
.
Дано:
h в
= 30см = 0,3м
ρ=0,9∙103
кг/м3
.
Найти:
Рабс
и Рвак
- ?
Решение:
1. Находим Рвак
из основного уравнения гидростатики:
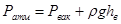
где Рвак
– вакуумметрическое давление, кг/м2
Ратм
– атмосферное давление, [Ратм
=105
кг/м2
]
g– ускорение свободного падения, [g=9,81 Н/кг]
h в
– высота поднятия жидкости в вакуометре, м
ρ – относительная плотность жидкости, кг/м3
Выражаем Рвак

Находим Рабс
как разность Ратм
и Рвак

Ответ: 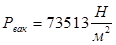 ; ; 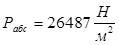
№5. Определить равнодействующую силу воздействия воды на плоскую стенку и точку ее приложения, если глубина воды слева Н=4м, справа h=1м, ширина стенки В= 1 м, угол наклона α= 50°.
Дано:
H = 4м
h = 1м
b = 1м
α = 50o
γ = 9,799Н/м3
Найти:
Pр
- ?
Решение:
1. Находим силу гидростатического давления:
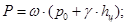
где Р – сила гидростатического давления, Н
ω – площадь свободной поверхности, [ω=b·h м2
]
ро
– атмосферное давление, [ро
=105
кг/м2
]
hц
– высота жидкости до центра резервуара, м
γ – удельный вес жидкости, [γ = ρ · g Н/м2
],
Находим силу гидростатического давления на стенку в резервуаре А


2. Находим плечо действия силы:
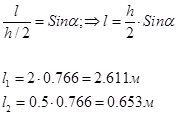
3. Находим плечо действия равнодействующей силы:
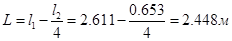
4. Находим величину действия сил Р1
и Р2
на плечо L:

5. Находим равнодействующую силу гидростатического давления Р

6. Находим высоту приложения равнодействующей силы гидростатического давления:
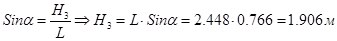
Ответ: Рр
= 419,556Н,
Н3
= 1,906м
№6. Определить диаметр D1
(см. рис 1) гидравлического цилиндра, необходимый для подъема задвижки при избыточном давлении жидкости р, если диаметр трубопровода D2
и вес подъемных частей устройства G=2кН. При расчете силой трения задвижки в направляющих пренебречь. Давление за задвижкой равно атмосферному.
Дано:
P=0,9 мПа
D2
=0,8 м
G=2кН
|
| D1
-? |
Решение:
1. 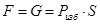 , ,
где 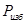 - избыточное давление жидкости, - избыточное давление жидкости, 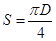 -площадь поверхности поршня. -площадь поверхности поршня.
2. 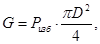
Отсюда
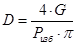 . .
3. В нашем случае
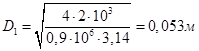
Ответ: 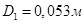
№7. Определить точку приложения, направление и значение равнодействующей силы воздействия на плоскую прямоугольную стенку, наклоненную к горизонту под углом 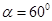 , если известны глубина воды Н и ширина стенки В (см. рис.2) , если известны глубина воды Н и ширина стенки В (см. рис.2)
Дано:
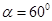
В=2,0 м
Н=1,2 м
|
НД
-?
P-?
|
Решение:
1. Определяем гидростатическую равнодействующую силу воздействия на плоскую прямоугольную стенку:
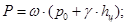
где Р – сила гидростатического давления, Н
ω – площадь свободной поверхности, [ω=b·h, м2
; 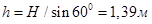 ] ]
ро
– атмосферное давление, [ро
=100 кН]
hц
– высота жидкости до центра резервуара,[ hц
=H/2=0,6 м]
γ – удельный вес жидкости, [γ = ρ g = 9,78929, кН/м3
],
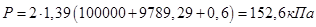
2. Определяем точку приложения равнодействующей силы:
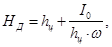 где где 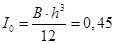

Ответ: НД
=0,87; Р=152,6 кПа.
№ 8. Определить абсолютное давление (см. рис. 1) в точке А закрытого резервуара с водой, если высота столба ртути в трубке дифманометра h, линия раздела между ртутью и водой расположена ниже точки В на величину h1
, а точка А - ниже точки В на 0,4 м.
Дано:
h=30см=0,3м
h1
=10мм=0,1м
h2
=0,4м
Р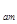 = 98.1 кПа = 98.1 кПа
g = 9.81 кН/м = 9.81 кН/м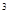
gрт
=133,331 кН/м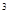
Решение:
Определяем абсолютное давление в закрытом резервуаре
Рв
= Р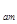 + gрт
h+g + gрт
h+g *h1
=98100+133331*0,3+9810*0,1=139080,3 Па *h1
=98100+133331*0,3+9810*0,1=139080,3 Па
Вычислим абсолютное давление в точке А
Рабса
= Р+ g *h =139080.3+9810*0.4=143004.3 Па
Ответ: 143004.3 Па
№9. У гидравлического пресса для получения виноградного сока диаметры цилиндров Dи d. Определить силу F1
(cм. рис. 1.2), действующую на большой поршень, если к малому приложена сила F= 200 Н
Дано:
d= 0.015 м
D= 0.32 м
F= 200 H
Решение:
S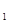 = = 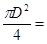 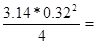 0.08м2 0.08м2
S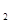 = =   =0,00017м2 =0,00017м2
F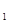 = = 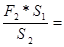 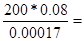 94117.6м2 94117.6м2
Ответ:94117,6
№10. В мультипликаторе - повысителя давления известны диаметры поршней D=20мм и d=6мм. Определить давление жидкости на выходе из мультипликатора р2
(см. рис. 2), если давление на входе р1
= 20кПа.
Дано:
D=0,045м
d=0,005м
р1
= 20кПа=2∙104
Па
Решение:
1. 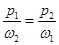
где р1
и р2
– давление на входе и выходе, Па, ω1
и ω2
– площади поршней на входе и выходе,м2
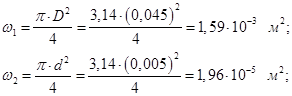
где Dи d– диаметры поршней, м
2. Выражаем давление на выходе р2
.
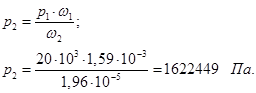
Ответ: р2
= 162,2 кПа
№ 11. Шлюзовое окно закрыто щитом треугольной формы с размерами а и b. За щитом воды нет, а глубина воды перед ним H = b. Определить равнодействующую силу воздействия воды на щит и положение центра давления (см. рис.).
Дано:
a= 0.7 м
b= 2 м
g=9.81 кН/м
Решение:
w= 1/2 ab= 0.7*2=0.7
hc
= 2/3 H= 2/3 *2=1.3
Рn
=w(r0
+ghc
)=0.7(9810*1.3)=8927.1
I0
=АВ3
/36 Уд
=hc
+ I0
/ hc
*w
I0
= АВ3
/36=0.15
Уд
=hc
+ I0
/ hc
*w=1.3+0.15/1.3*0.7=1.46
Ответ: Рn
=8927.1 и Уд
=1.46
№12
Дано:

Решение:

Ответ: 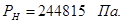
|