Обращаясь к основным дифференциальным уравнениям колебаний, мы заметим, что когда умножим их на – = к2
, они будут содержать члены, из которых одни имеют коэффициентом квадрат скорости и
поперечных колебаний, другие – квадрат скорости продольных
колебаний.
Первые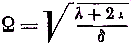 члены в случае колебаний продольных должны исчезнуть из уравнений, и мы получаем первую группу:
члены в случае колебаний продольных должны исчезнуть из уравнений, и мы получаем первую группу:
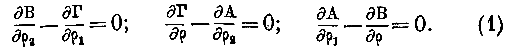
Так как поверхность p по нашему выбору есть поверхность волны, то в уравнениях § 7 мы должны удержать одно колебание R
и приравнять нулю колебания /?! и R.2
,
совершающиеся в плоскости, касательной к волне. Вследствие этого находим, полагая // =1:
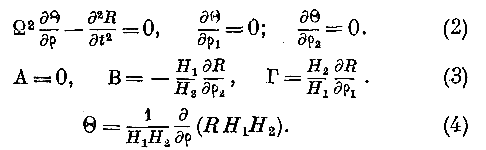
Так как А = 0, то уравнения (1) примут вид:
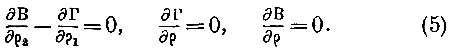
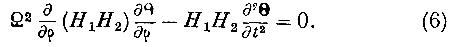
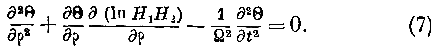
Умножая первое из уравнений (2) на //i //2
, дифференцируя по p и обращая внимание на уравнение (4), находим:
что
по уравнениям (2) В не зависит ни от рх
, ни от [–]. Следовательно, означая через &F
частную производную от функции F
по одной из переменных ^,
р.2
, мы получаем из уравнения (7):
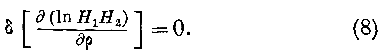
Подставляя в это выражение величины Н1
Н2
,
найденные в п.п. 3, приравнивая нулю коэффициенты при различных степенях, мы находим следующие условия, которым должна удовлетворять волновая Ф – я
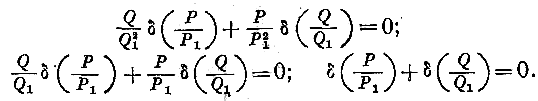
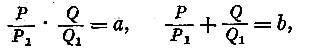
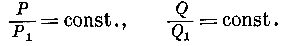
Известно,
что подобные соотношения имеют место только для сферы, круглого цилиндра и плоскости.
Отсюда имеем,
что изотермические волновые поверхности могут распространять колебания продольные.
Итак, если поверхность сотрясения или начальная волна не принадлежат к поверхностям изотермических волн, то вблизи их колебания происходят смешанные
, но на значительных расстояниях волна приближается к виду одной из изотермических волн, и в явлении обнаруживаются колебания продольные. СТОП!!!
Остается проинтегрировать приведенные дифференциальные уравнения для сферы, с использованием гармонических функций!!!
Эксперименты Теслы –
гармонический осциллятор – недопустим!!!
Для сферы
в координатах, уже нами употреблённых, мы имеем:
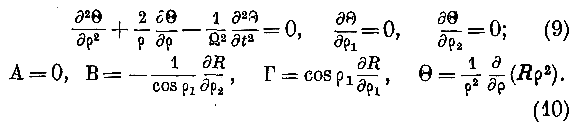
Дальнейшие преобразования несущественны и не приводятся, так как приводят к исходному уравнению
, не имеющему физического смысла для солитоноподобных волн.
Найденные выводы одинаково применимы к явлениям света в телах однородных и притом в тех пределах приближения, которые имеют место в теории Буссинеска!?
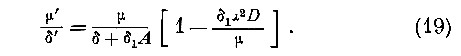
Отсюда:
«болевой момент»
выявлен.
Н. Умов математический сборник, т. 5, 1870 г. [7].
Ещё одна «страшная» неопределённость
Рассуждая аналогично, можно было бы легко получить подобное же выражение и для магнитной энергии, а следовательно и для токов. Мы видим, что, даже настаивая на самой простой из формул, проблему локализации энергии по-прежнему не удаётся решить
.
И то же самое имеем для потока энергии. Можно преобразовать движение текущей энергии произвольным образом, добавляя к вектору Пойнтинга другой вектор (u, v, w), обязанный удовлетворять лишь уравнению несжимаемых жидкостей

Откуда:

Теорема Пойнтинга
, являющаяся следствием общих уравнений, ничего к ним не добавляет.
Поэтому локализация энергии логически бесполезна
(а иногда, вредна).
Но имеется аспект, в котором важно рассмотреть теорему Пойнтинга.
Основным фактом, из которого проистекает закон сохранения энергии, был и остаётся экспериментально найденный факт невозможности вечного движения
, факт – независимо от наших идей, и может, быть отнесён к порциям энергии, которой должен обладать эфир в отсутствие материальных тел.
Закон сохранения энергии [4], в его классической форме W
=
Const
, объясняет эту невозможность.
Теорема Пойнтинга
, требующая возможности преобразования объёмного интеграла
(отчасти произвольного) в поверхностный,
выражает гораздо меньше. Она легко допускает создание вечного движения, не будучи способна показать его невозможность
!
По сути, пока мы не введём гипотезу запаздывающих потенциалов
, непрерывное выделение энергии сходящихся волн, приходящих из бесконечности, остаётся столь же вероятным, сколь и потеря энергии, наблюдаемая в действительности.
Если бы двигатель мог вечно забирать одну лишь энергию эфира, независимо от присутствия материальных тел, то могло бы существовать и вечное движение
. Таким образом, становится ясно, что прежде чем принять формулу запаздывающих потенциалов, мы должны доказать, что ускоренная частица теряет энергию и в результате подвергается противодействию, пропорциональному производной ее ускорения [13].
Достаточно лишь изменить знак c
, чтобы прийти к гипотезе сходящихся волн.
Тогда мы обнаружим
, что знак вектора излучения
также изменится, и новая гипотеза приведёт, скажем, в случае вибрирующей частицы, к постепенному увеличению амплитуды с течением времени, а в целом – к увеличению энергии системы?!
В Природе солитоны бывают:
– на поверхности жидкости первые солитоны, обнаруженные в природе, иногда считают таковыми волны цунами
– различные виды гидроудара
– звуковые ударные – преодоление «сверхзвука»
– ионозвуковые и магнитозвуковые солитоны в плазме
– солитоны в виде коротких световых импульсов в активной среде лазера
– предположительно, примером солитона является Гигантский гексагон на Сатурне
– можно рассматривать в виде солитонов нервные импульсы [32], [49].
Математическая модель, уравнение Кортевега-де Фриза.
Одной из простейших и наиболее известных моделей, допускающих существование солитонов в решении, является уравнение Кортевега-де Фриза:
ut
+ uux
+ βuxxx
= 0.
Одним из возможных решений данного уравнения является уединённый солитон
:
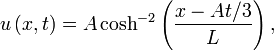 но и здесь осцилятором является гармоническая функция но и здесь осцилятором является гармоническая функция
Кубическое уравнение Шрёдингера
Для нелинейного уравнения Шрёдингера:
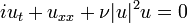
при значении параметра ν > 0 допустимы уединённые волны в виде:
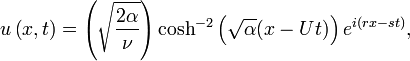
где r
, s
,α, U
– некоторые постоянные.
Теоремы неопределённости в гармоническом анализе
Гармонический осциллятор
в квантовой механике – описывается уравнением Шредингера
[38], [79]
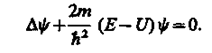 (217.5) (217.5)
Уравнение (217.5)
называется уравнением Шредингера для стационарных состояний.
Стационарные состояния квантового осциллятора определяются уравнением Шредингера
вида
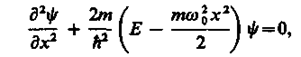 (222.2) (222.2)
где Е
– полная энергия осциллятора.
В теории дифференциальных уравнений доказывается, что уравнение (222.2)
решается только при собственных значениях энергии
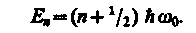 (222.3) (222.3)
Формула (222.3)
показывает, что энергия квантового осциллятора квантуется.
Энергия ограничена снизу отличным от нуля, как и для прямоугольной «ямы»
с бесконечно высокими «стенками» (сМ. § 220), минимальным значением энергии
E
0
= 1/2
ℏ
w
0
.
Существование минимальной энергии – называется энергией нулевых колебаний
– является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей.
В гармоническом анализе
принцип неопределённости подразумевает, что нельзя точно получить значения функции и её отображения Фурье – а значит и сделать точный расчёт
.
То есть моделирование, генерация и аналогия с соблюдением принципов подобия процессов и форм в Природе, с применением гармонического осцилятора
– не возможна.
Разных видов математических
солитонов
известно пока мало и все они не подходят для описания объектов в трехмерном
пространстве, тем более процессов происходящих в Природе.
Например
, обычные солитоны
, которые встречаются в уравнении Кортевега–де Фриза, локализованы всего лишь в одном измерении, если его «запустить»
в трехмерном мире, то он будет иметь вид летящей вперед бесконечной плоской мембраны,
мягко говоря абракадабра!!!
В природе, такие бесконечные мембраны не наблюдаются, а значит, исходное уравнение
для описания трехмерных объектов не годится.
Вот здесь и заключается ошибочность введения гармонических функций – осцилляторов, связи в случае смешанных колебаний.
Связной закон подобия
[54], [54],
но это уже другая история, которая выведет, теорию солитонов из систематической
неопределённости
[38], [39].
Считаю, что не всё так плохо – имеется целый огромный пласт «неизученной»
теории и методов Н. Тесла, на означенную тему, тем более, что математический аппарат давно подготовлен к изучению и решению проблем визуализации ударных волн.
|