КУРСОВАЯ РАБОТА
с дисциплины: “Элементы и системы автоматического контроля и управления"
на тему: “Синтез и построение системы управления нестационарными динамическими объектами"
Содержание
Введение
1.Синтез системы управления квазистационарным объектом
1.1 Математическая модель нестационарного динамического объекта
1.2 Представление схемы переменных состояний в форме Коши
1.3 Нахождение передаточных функций звеньев системы управления
1.4 Построение логарифмических амплитудно-частотных и фазочастотных характеристик
2.Синтез скорректированной квазистационарной системы
2.1 Построение желаемых логарифмических амплитудно-частотных и фазочастотных характеристик
2.2 Построение логарифмической амплитудно-частотной характеристики корректирующего звена системы
3.Разработка структурной и принципиальной схем управления нестационарным динамическим объектом
3.1 Разработка структурной схемы устройства
3.2 Разработка и расчет принципиальной схемы
Заключение
Список литературы
Информация об объекте управления может быть получена путем измерения соответствующих параметров. Однако не все параметры могут быть непосредственно измерены из-за отсутствия необходимых средств измерения или недопустимости этих параметров для контроля.
Это приводит к снижению качества управления, и особенно проявляется при управлении объектами, параметры которых являются функциями времени. Такие объекты принято называть нестационарными динамическими объектами.
Однако проблема построения информационно-управляющих систем нестационарных динамических объектов (НДО), а также проблема комплексной оценки анализа параметрического и фазового состояния объектов с неизвестными и переменными во времени динамическими характеристиками, и неполным вектором измерения фазовых координат, не нашли должного освещения в современной литературе. В тоже время целесообразность решения этих задач становиться очевидной.
Особое внимание в данной работе отводится анализу обоснования выбранных методов и критериев, принципа функционирования, оценки результатов и рекомендаций о возможных путях повышения систем автоматического управления.
По заданному нестационарному дифференциальному уравнению, которым описывается поведение объекта управления, находится параметрическая функция. Выбирается метод решения синтеза системы с учетом ограничений.
Методом квазистационарности находим передаточную функцию объекта и по заданным показателям качества переходного процесса строим желаемую ЛАЧХ скорректированной системы, а затем находим передаточную функцию, схему и параметры корректирующего устройства.
1
.Синтез системы управления квазистационарным объектом
Для представления динамического процесса заданного системой дифференциальных уравнений в переменных состояния решим её относительно старшей производной:
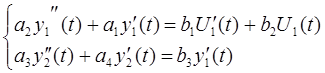 , (1.1) , (1.1)
 . (1.2) . (1.2)
Полученная система дифференциальных уравнений (1.2) представляет собой структуру динамического процесса в переменных состояния
Анализ системы (1.2) показывает, что объект управления содержит: два сумматора складывающих все компоненты входящие в динамический процесс. На вход сумматоров подаётся составляющая входного возмущения, реакция объекта и составляющая производная от реакции объекта.
Схема динамического процесса в переменных состояния будет иметь вид.
Рисунок 1 - Схема динамического процесса в переменных состояния

Представим систему дифференциальных уравнений в векторно-матричной форме.
Z′ (t) = A*Z (t) +B*U (t), (1.3)
где матрица А - динамическая матрица объекта управления, которая характеризует динамику объекта;
Z (t) - вектор фазового состояния;
В - матрица управляющих (возмущающих) объекта, которая характеризует степень возмущения (управления);
U (t) - вектор возмущения.
Для нахождения динамической матрицы, вектора состояния, матрицы управляющих объекта, вектора возмущений введем некоторую переменную Z (t), и воспользуемся преобразованием Коши для системы дифференциальных уравнений (1.1):
 , (1.4) , (1.4)
тогда система (1.2) примет вид:
 . (1.5) . (1.5)
Перейдем от системы уравнений (1.5) к векторно-матричной форме:
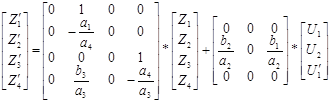 . (1.6) . (1.6)
Таким образом, выражение (1.3) описывает поведение объекта управления в переменных в параметрическом и фазовом пространствах.
Для того чтобы найти передаточные функции системы запишем исходную систему в операторной форме
 (1.7) (1.7)
и разрешим её относительно реакций динамического процесса у1
и у2
 , (1.8) , (1.8)
откуда находим для первого уравнения
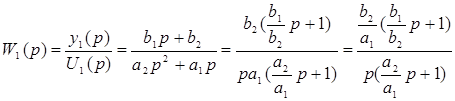 , (1.9) , (1.9)
или 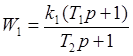 , ,
где  ; ;  ; ;  ; ;
для второго уравнения
 (1.20) (1.20)
или  , ,
где 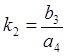 ; ;  . .
Подставляя значения коэффициентов находим параметры звеньев системы
k1
= 0,5; k2
= 0,42;
T1
= 44 с; Т2
= 0,1 с;
Т3
= 0,025 с.
Полученная система описывает структуру исходного динамического процесса в передаточных функциях. Структура процесса имеет следующий вид
Рисунок 2 - Структура исходного динамического процесса
Исходя из того, что показатель астатизма pn
выбираем пропорциональный регулятор.
Коэффициент передачи всей системы равен
kv
= 1/c = 1/0,008 = 125;
kv
= k1
∙k2
∙kp
; (1.21)
kp
= kv
/ (k1
∙k2
) = 595,28.
Находим частоты сопряжения исходной разомкнутой системы
ωi
= 1/Тi
, где i = 1, 2, …,
тогда ω1
= 0,0227 с-1
;
ω2
= 10 с-1
;
ω3
= 40 с-1
.
Передаточная функция всей системы будет иметь вид
Wпс
(p) = W1
(p) ∙W2
(p) ∙Wр
(p) (1.22)
Построение ЛAЧХ и ЛФЧХ данной системы (см. приложение 1):
на оси ординат откладываем коэффициент передачи в децибелах
K (дб) = 20 lgkv = 20 lg 125 = 41,93 дб;
по оси абсцисс откладываем частоты;
поскольку знаменатель передаточной функции состоит из двух множителей с коэффициентом астатизма 1, то прямая проходящая через точку 41,93 на оси ординат, будет иметь наклон - 20 дб/дек до первой частоты сопряжения ω1
. Следующая прямая имеет наклон +20 дб/дек по отношению к предыдущей (форсирующее звено). Третья прямая будет иметь наклон -20 дб/дек по отношению к предыдущей (апериодическое звено). Четвертая прямая будет иметь наклон -20 дб/дек по отношению к предыдущей (апериодическое звено) с продлением в область высоких частот.
ЛАЧХ и ЛФЧХ данной системы будут иметь следующий вид
L (ω) = 20 lgkv
+ 20 lgω2
- 20 lgω1
- 20 lgω3;
φ (ω1
) = - π +arctg ω1
- arctg ω2
-arctg ω3.
В результате построения частотных характеристик и сложения фазочастотных характеристик видим, что данная разомкнутая нескорректированая система не имеет запаса ни по амплитуде, ни по фазе, следовательно, необходимо строить корректирующее звено.
2
.Синтез скорректированной квазистационарной системы
При построении желаемой ЛАЧХ целесообразно выделить три области частот: область низких, область средних и область высоких частот.
В интервале низких частот вид ЛАЧХ указывает на порядок астатизма и статическую точность системы. При частотах, меньших первой сопрягающей частоты ЛАЧХ имеет наклон 20υ дб/дек, где υ - порядок астатизма системы.
Интервал средних частот лежит между первой и второй сопрягающими частотами, т.е.
ω1к
≤ ωср
≤ ω2к
,
ω2к
= (3 - 4) ∙ωср
,
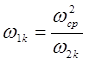 , (1.23) , (1.23)
 , ,
где tр - время регулирования квазистационарной системы;
β - коэффициент, зависящий от величины перерегулирования σ%, определяемый по графику зависимости (рис.3).
Рисунок 3 - График зависимости коэффициента β (σ %)
Выбираем коэффициент β = 3.2, тогда
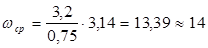 с-1
; с-1
;
ω2к
= 3,5 ωср
= 3,5 13,39 = 46,89 ≈ 47 с-1
;
ω1к
= 4,17 ≈ 4 с-1
.
Таким образом, определив все частоты, строим желаемую ЛАЧХ из таких соображений:
В области низких частот наклон ЛАЧХ -40дб/дек, в области средних частот наклон ЛАЧХ имеет -20 дб/дек, в области высоких частот наклон ЛАЧХ совпадает с наклоном ЛАЧХ нескрорректированной системы, поскольку на переходной процесс она большого влияния не оказывает.
По виду желаемой ЛАЧХ строим фазочастотные характеристики.
Учитывая то, что передаточная функция разомкнутой скорректированной системы определяется выражением.
Wск = Wнс (p) Wкз (p), (1.24)
получаем, что
Wкз (jω) = Wск (jω) /Wнс (jω). (1.25)
Прологарифмируем (1.25) и получим
lgWкз (jω) = lgWск (jω) - lgWнс (jω). (1.26)
Из выражения следует, что ЛАЧХ корректирующего устройства квазистационарной системы равна разности ЛАЧХ скорректированной и нескоректированной системы равна разности ЛАЧХ скорректированной и нескорректированной ЛАЧХ соответственно. Таким образом, вычитая ординаты ЛАЧХ нескорректированной системы и ординат желаемой ЛАЧХ на частотах сопряжения, получим ординаты ЛАЧХ корректирующего устройства.
Передаточная функция корректирующего звена будет иметь вид
 . (1.27) . (1.27)
3
.Разработка структурной и принципиальной схем управления нестационарным динамическим объектом
Анализируя графики логарифмических амплитудно-частотных характеристик нескорректированной разомкнутой системы и корректирующего звена мы можем выделить основные блоки из которых состоит полученная система управления нестационарным динамическим объектом: нескорректированная система содержит форсирующее звено и два апериодических звена, а корректирующие звенья включаются в отрицательную обратную связь и делают нескорректированную разомкнутую систему замкнутой скорректированной системой управления нестационарного динамического объекта.
Структурная схема скорректированной замкнутой системы управления нестационарным динамическим объектом приведена на рис.4.
Рисунок 4 - Структурная схема замкнутой системы
В качестве элементной базы для реализации структурной схемы замкнутой скорректированной системы управления выбираем операционный усилитель типа К140УД7, с параметрами
Uпит
= ±15, Iвх
= 200 нА, Кос
= 60 дБ, f = 0,8МГц, Uвых.
max
= 10.5 В,
Rвх
= 0.4Мом, Ku = 5·104
.
Основные звенья, которые используются в разработанной системе это: сумматор, усилительное звено, апериодическое звено и форсирующее звено.
Сумматор.
Внешний вид сумматора представлен на рисунке рис.4.

Рисунок 4 - Сумматор на основе операционного усилителя
Резисторы R1
= R2
=R3
= R4
= 20 кОм.
Усилительное звено.
Данное звено усиливает входной сигнал до уровня, необходимого для срабатывания логический элементов.

Рисунок 5 - Усилительное звено на основе операционного усилителя
Принимаем R1
= 20 кОм, тогда R2
будет равным
R3
= k*R1
.
R2
= (R1
*R3
) / (R1
+R3
). (1.28)
Тогда для кр
= 595,28, R3
= 20000* 595,28 = 12 МОм, R2
= 20 кОм;
Апериодическое звено.
Апериодическое звено первого порядка используемое в разрабатываемом устройстве приведено на Рис.6.

Рисунок 6 - Апериодическое звено на основе операционного усилителя
Постоянная времени апериодического звена равна
T= R*C, (1.29)
откуда прияв R1
=R3
= 20 кОм найдем
R2
= R1
/2 =10 кОм, (1.30)
Сi
= Ti
/R1
.
Для T2
= 0.1 c, С = 5 мкФ; Т1
= 44 с, С = 2.2 мФ;
Т3
= 0.025 с, С = 1,25 мкФ; Т2к
= 0.021 с, С = 1.05 мкФ.
Форсирующее звено.

Рисунок 7 - Форсирующее звено на основе операционного усилителя
Задаемся R1
= R3
= 20 кОм, тогда
R2
= R1
/2 = 10 кОм,
Сi
= Ti
/R1
. (1.31)
Для Т1
= 44с, С = 2.2 мФ; Т2
= 0.1с, С = 5 мкФ;
Т1к
= 0.25с, С = 12.5 мкФ; Т3
= 0.025с, С = 1.25 мкФ.
Принципиальная схема разработанного устройства приведена чертеже Э3.
При построении системы автоматического управления использовалось несколько методов исследования объекта управления.
Метод пространства состояний позволил представить нестационарный объект управления схемой в пространстве состояний, определить вектор состояния, вектор изменения, динамическую матрицу параметров и провести исследование объекта при различных возмущающих и управляющих воздействиях, а также определить область управляемости при фиксированных возмущающих воздействиях.
Метод квазистационарности был применен для нахождения передаточной функции квазистационарного объекта и построения желаемой логарифмической амплитудно-частотной характеристики скорректированной системы по показателям качества переходного процесса, а также нахождения передаточной функции, схемы и параметров корректирующего звена.
В результате нами была разработана система автоматического управления нестационарным динамическим объектом, которая имеет достаточный запас как по фазе, так и по амплитуде.
1. Барковский В.В. и др. Методы синтеза систем управления. - М.: Машиностроение, 1969.
2. Володченко Г.С. Синтез адаптивной системы оптимального управления нестационарным объектом одного класса. - Республиканский науч.-тех. Сб. АСУ и приб. Автоматики. Вып.50 - Высшая школа, 1978.
3. Воронов А.А. и др. Теория автоматического управления. - М.: Высш. шк., 1977.
4. Солодов А.В., Петров Ф.С. Линейные автоматические системы с переменными параметрами. - М.: Наука, 1971.
|