Содержание
Введение
Глава 1.Электронный спектр двустеночной углеродной нанотрубки
Глава 2. Проводимость двустеночной углеродной нанотрубки
Выводы
Список использованных источников
Приложение
Введение
Современная металло-оксидно-полупроводниковая микроэлектроника фактически достигла пределов быстродействия и степени интеграции. Дальнейшее развитие электроники связывают с уменьшением размеров устройств до наномасштабов с использованием новой элементной базы. Поэтому на сегодняшний день большой интерес вызывают так называемые квазиодномерные системы, примерами которых являются полимеры, нанотрубки на основе углерода, кремния и других материалов. В настоящее время нанотрубки уже выпускаются серийно многими фирмами, например, SES Research, Carbon Solutions Inc., Helix Material Solutions в США.
Нанотрубки бывают одностеночными и многостеночными. Одностеночная нанотрубка представляет собой графитовую плоскость, различным образом свернутую в цилиндр. Она характеризуется так называемыми индексами хиральности, и в зависимости от этих индексов может быть как металлом, так и полупроводником. Диаметр такой трубки порядка нанометров, а длина достигает микрометров, поэтому она занимает промежуточное положение между молекулой и кристаллом, что проявляется в наличии специфических свойств, в частности, зонной структуры в спектре электронов. Одностеночные нанотрубки уже достаточно хорошо изучены.
Многостеночная нанотрубка представляет собой либо несколько одностеночных трубок, вложенных друг в друга, либо графитовую плоскость, свернутую в несколько слоев в виде свитка, либо цилиндрическую структуру, составленную из небольших графитовых фрагментов и напоминающую папье-маше. В отличие от одностеночных, свойства многостеночных нанотрубок изучены намного хуже.
Целью данной работы является исследование спектров элементарных возбуждений двупериодических одномерных систем, примером которых являются двуслойные углеродные нанотрубки. Для этого с помощью метода сильной связи рассматривается спектр упрощенной модели нанотрубки в виде двух параллельных цепочек атомов, определяется уровень Ферми такой системы и исследуется ее проводимость. Все вычисления производились в программе, написанной на языке C++ в среде Microsoft Visual Studio 2008 с использованием библиотек Win32.
Глава 1. Электронный спектр двустеночной углеродной нанотрубки
Для исследования электронного спектра двустеночной углеродной нанотрубки воспользуемся моделью, в которой нанотрубка представляет собой две параллельные регулярные цепочки атомов с разными периодами. При этом, однако, в силу периодичности системы будем пользоваться результатами теоремы Блоха, поэтому необходимо потребовать, чтобы отношение периодов цепочек выражалось рациональной дробью.
Сначала рассмотрим систему, представляющую собой линейную цепочку атомов, расстояние между которыми а
, и определим энергетический спектр электрона в такой системе.
Будем пользоваться приближением сильной связи и искать волновую функцию электрона в виде:
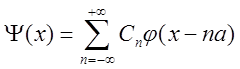 ,в (1.1) ,в (1.1)
где 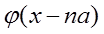 - волновая функция электрона на изолированном n
-ом атоме цепочки. Для удобства обозначим - волновая функция электрона на изолированном n
-ом атоме цепочки. Для удобства обозначим  . Далее, минимизируя функционал энергии при условии нормировки волновых функций . Далее, минимизируя функционал энергии при условии нормировки волновых функций  : :
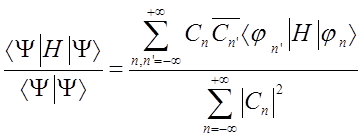 (1.2) (1.2)
получим:
 (1.3) (1.3)
Выделим в потенциальной энергии слагаемые с 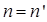 и воспользуемся тем, что решения для электронов на изолированном атоме известны: и воспользуемся тем, что решения для электронов на изолированном атоме известны:
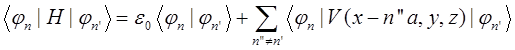 , (1.4) , (1.4)
где  - обменный интеграл. Далее учтем, что в методе сильной связи он считается ненулевым только для ближайших соседей, и получим: - обменный интеграл. Далее учтем, что в методе сильной связи он считается ненулевым только для ближайших соседей, и получим:
 (1.5) (1.5)
 (1.6) (1.6)
В силу трансляционной симметрии волновую функцию можно выбрать так, чтобы она удовлетворяла теореме Блоха, тогда коэффициенты  будут иметь вид будут иметь вид  . Подставим их в (1.6) и получим выражение для энергетического спектра электрона: . Подставим их в (1.6) и получим выражение для энергетического спектра электрона:
 (1.7) (1.7)
где 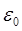 - энергия основного состояния электрона в изолированном атоме, к
– волновой вектор. - энергия основного состояния электрона в изолированном атоме, к
– волновой вектор.
Теперь рассмотрим две такие цепочки атомов, расположенные на некотором расстоянии d
друг от друга. Расстояние между атомами в первой цепочке по-прежнему a
, во второй – b
. Если пренебречь возможностью перескока электрона с одной цепочки на другую, то собственные волновые функции электронов будут иметь следующий вид:
 - описывает движение электрона с энергией - описывает движение электрона с энергией 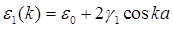 по первой цепочке; по первой цепочке;
 - описывает движение электрона с энергией - описывает движение электрона с энергией  по второй цепочке; по второй цепочке;
Теперь учтём, что при таком расположении цепочек появляется вероятность перескока электрона с одной из них на другую. Тогда в гамильтониане системы появятся недиагональные вклады:
 , (1.8) , (1.8)
где  - матричные элементы оператора взаимодействия, ответственного за перескок электронов. Считая его достаточно малым, вычислим поправки к энергии, воспользовавшись теорией возмущения для вырожденного уровня. Волновую функцию системы представим в виде линейной комбинации - матричные элементы оператора взаимодействия, ответственного за перескок электронов. Считая его достаточно малым, вычислим поправки к энергии, воспользовавшись теорией возмущения для вырожденного уровня. Волновую функцию системы представим в виде линейной комбинации  . Тогда соответствующее секулярное уравнение примет вид: . Тогда соответствующее секулярное уравнение примет вид:
 (1.9) (1.9)
Отсюда получим энергию нашей системы:
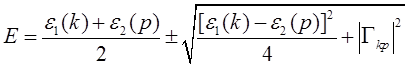 (1.10) (1.10)
Уровень Ферми в такой системе расщепляется. Это следует из того, что значения интегралов перекрытия γ1
и γ2
принимают разные значения, вследствие этого происходит перекрытие зон. Формула для энергии уровня Ферми упростится, если мы будем считать, что на нем выполняется условие:
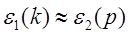 (1.11) (1.11)
и примет вид:
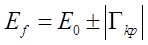 (1.12) (1.12)
Осталось вычислить  . Очевидно, что вероятность перескока электрона с одной цепочки на другую определяется расстоянием между атомами этих цепочек и быстро убывает с его ростом. Поэтому смоделируем . Очевидно, что вероятность перескока электрона с одной цепочки на другую определяется расстоянием между атомами этих цепочек и быстро убывает с его ростом. Поэтому смоделируем  в таком виде: в таком виде:
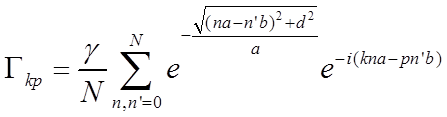 (1.13) (1.13)
Значение этого выражения определяется численно в программе. Импульсы k
и p
на уровне Ферми определяются из условия равенства энергий (1.11). Значения интегралов перекрытия брались из [1], [2].
Глава 2. Проводимость двустеночной углеродной нанотрубки
Как было показано в [3], в упрощенной модели одностеночной трубки, представляющей собой линейную цепочку атомов, сила протекающего через нее тока определяется выражением:
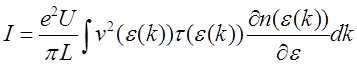 , (2.1) , (2.1)
где U
- напряжение, приложенное к концам трубки, L
– ее длина, τ
– время релаксации электронов, n
– их концентрация. После простых преобразований получим:
 (2.2) (2.2)
Так как мы рассматриваем идеальную систему, то рассеяние электронов при движении может происходить только на контактах. Тогда время релаксации электронов можно определить так:
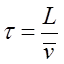 (2.3) (2.3)
Тогда формула приобретет простой вид:
 (2.4) (2.4)
Видно, что электрическое сопротивление одностеночной нанотрубки обладает уникальным свойством – оно не зависит от геометрических размеров и определяется величиной  - квантом сопротивления (формула Ландауэра [4], [5]). Такое сопротивление называется баллистическим. - квантом сопротивления (формула Ландауэра [4], [5]). Такое сопротивление называется баллистическим.
Рассмотрим теперь проводимость двустеночной нанотрубки.
В предыдущей главе было показано, что гамильтониан системы из двух линейных регулярных цепочек атомов с учетом их взаимодействия имеет вид:
 (2.5) (2.5)
Собственными волновыми функциями такого гамильтониана будут функции:
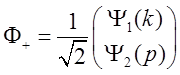 , , 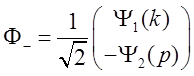 (2.6) (2.6)
Волновую функцию электрона, влетающего в первую цепочку, представим в виде линейной комбинации этих волновых функций:
 (2.7) (2.7)
Рассмотрим теперь эволюцию этой волновой функции во времени. По правилам квантовой механики, получим:
 , (2.8) , (2.8)
где под Δ для удобства обозначено |Γkp
|.
Учитывая ортогональность функций Ψ1
и Ψ2
, которые для электронов имеют вид блоховских функций, следуя [6], получим для средней скорости первого электрона на уровне Ферми:
 (2.9) (2.9)
или, с учетом того, что 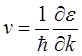
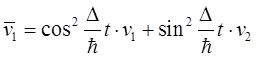 (2.10) (2.10)
То есть, скорость электрона на уровне Ферми является суперпозицией двух слагаемых, в которых присутствуют скорости на уровне Ферми для первой изолированной цепочки и для второй. Аналогично, для второй цепочки:
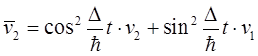 (2.11) (2.11)
Рассмотрим два граничных случая, когда  и и  . .
В первом случае усреднением заменяем 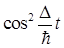 и и 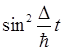 на 1/2: на 1/2:
 (2.12) (2.12)
Во втором случае  , ,  : :
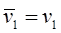 (2.13) (2.13)
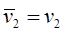 (2.14) (2.14)
Сразу видно, что во втором случае в выражении для времени релаксации электронов не будет никаких изменений, не изменится вид формулы (2.2), а значит, и формула Ландауэра не изменится.
Рассмотрим подробнее первый случай. Проводимость системы из двух параллельных одностеночных трубок определяется выражением:

 (2.15) (2.15)
Проводимость двустеночной трубки:

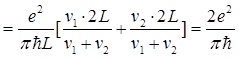 (2.16) (2.16)
Видно, что и в этом случае формула Ландауэра остается справедливой.
Выводы
Целью данной работы было исследование электронного спектра и проводимости в двустеночных нанотрубках. С помощью упрощенной модели, представляющей собой две параллельные регулярные цепочки атомов, было показано, что в таких нанотрубках происходит перекрытие зон, что приводит к изменению положения уровня Ферми, а также его расщеплению. Величина этого расщепления была определена численно в программе, листинг которой приведен в приложении. При реалистичных значениях параметров расщепление оказалось достаточно малым, порядка 10-5
эВ. При этом изменяется и скорость электронов на уровне Ферми. Очевидно, что в такой идеальной системе рассеивание электронов должно происходить на контактах, поэтому время релаксации будет зависеть только от средней скорости движения электронов. Было проанализировано выражение для средней скорости движения электронов и показано, что в предельных случаях высоких и низких частот в двустеночных системах формула Ландауэра остается справедливой.
Список использованных источников
1. Wildoer J.W.G., Venema L.C., Rinzler A.G., Smalley R.E., Dekker C. Electronic structure of atomically resolved carbon nanotubes // Nature – 1998. – V.391. – P.59 -62.
2. Odom T.W., Huang J.L., Kim P., Lieber C.M. Structure and electronic properties of carbon nanotubes // J. Phys. Chem. B – 2000. – V.104(13). – P.2794-2809.
3. Тищенко С.В. Зонная структура и межзонные переходы в углеродных нанотрубках: Дис., 01.04.02 – Одесса, 2007. - 100 с.
4. Landauer R. Electrical resistance of disordered one-dimensional lattices // Phyl. Mag. – 1970. – V.21 – No 172. – P.863-867.
5. Buttiker M., Imry Y., Landauer R., Pinhas S. Generalized many-channel conductance formula with application to small rings // Phys. Rev. B – 1985. – V.31. – P.6207-6215.
6. Ансельм А.И. Введение в теорию полупроводников – М.: Наука, 1978. – 616 с.
Приложение А. Алгоритм программы для вычисления величины расщепления в спектре упрощенной модели двуслойной нанотрубки в виде двух параллельных цепочек атомов
Содержимое файла stdafx.h:
#include <stdio.h>
#include <tchar.h>
#include <math.h>
class Complex
{
public:
double real;
double image;
Complex() {}; // Конструктор по умолчанию
Complex(double r) { real = r; image = 0; } // Конструктор
Complex(double r, double i) { real = r, image = i; } // Конструктор
~Complex() {} // Деструктор
double absolute() // Модуль комплексного числа
{
return sqrt(real * real - image * image);
}
Complex operator+(Complex &); // Перегрузка оператора сложения
Complex operator-(Complex &); // Перегрузка оператора вычитания
Complex operator*(Complex &); // Перегрузка оператора умножения
Complex operator/(Complex &); // Перегрузка оператора деления
};
Содержимое файла Gammakp.cpp:
#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;
#define N 30
#define a 1.0
#define b 1.1
#define в 0.5
// Перегрузка +
Complex Complex::operator+(Complex &fp1)
{
fp1.real = real + fp1.real;
fp1.image = image + fp1.image;
return fp1;
}
// Перегрузка -
Complex Complex::operator-(Complex &fp1)
{
fp1.real = real - fp1.real;
fp1.image = image - fp1.image;
return fp1;
}
// Перегрузка *
Complex Complex::operator*(Complex &fp1)
{
double i, j;
i = real * fp1.real - image * fp1.image;
j = real * fp1.image + fp1.real * image;
fp1.real = i;
fp1.image = j;
return fp1;
}
// Перегрузка /
Complex Complex::operator/(Complex &fp1)
{
double k, i, j;
k = fp1.real * fp1.real + fp1.image * fp1.image;
i = (real * fp1.real + image * fp1.image) / k;
j = (fp1.real * image - real * fp1.image) / k;
fp1.real = i;
fp1.image = j;
return fp1;
}
int main()
{
Complex Gkp;
double m;
int i,j;
for(i=0;i<N;i++)
for(j=0;j<N;j++)
{
Gkp.real=0;
Gkp.image=0;
Gkp.real=Gkp.real+1/(double)N*exp(-1/a*sqrt(pow(i*a-j*b,2)+d*d))*cos(6.28*i-6.28*j);
Gkp.image=Gkp.image-1/(double)N*exp(-1/a*sqrt(pow(i*a-j*b,2)+d*d))*sin(6.28*i-6.28*j);
}
Gkp.real=pow(Gkp.absolute(),2);
cout<<"Gkp"<<" "<<Gkp.real<<"\n";
getchar();
}
|