БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
кафедра РЭС
реферат на тему:
«Особенности практического применения способов кодирования. Способы декодирования с обнаружением ошибок»
МИНСК, 2009
Задача кодирования заключается в формировании по информационным словам a(x) кодовых слов (x) циклического (n,k)-кода, который по своей структуре может быть несистематическим и систематическим.
Формирование кодовых слов несистематического кода заключается в умножении многочлена a(x), отображающего информационную последовательность длины k, на порождающий многочлен, т.е. (x)=a(x)(g(x). Формирование кодовых слов систематического кода заключается в преобразовании информационной последовательности a(x) в соответствии с выражением (x)=a(x)xr
+r(x).
Проверочная последовательность r(x) определяется двумя способами:
при использовании "классического" способа кодирования 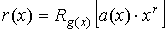 ; ;
при использовании способа кодирования, рекомендованного МККТТ 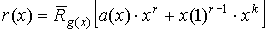 , ,
где x(1)r-1
- единичный многочлен степени (r-1).
Указанные выше математические операции выполняют кодеры несистематического и систематического кодов.
Способы декодирования с обнаружением ошибок
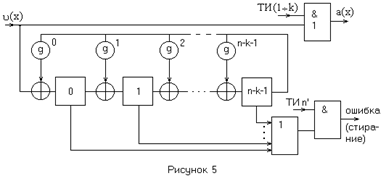
Процедура декодирования циклического кода с обнаружением ошибок, по аналогии с процессом кодирования, использует два способа:
- при кодировании "классическим" способом декодирование основано на использовании свойства делимости без остатка кодового многочлена (x) циклического (n,k)-кода на порождающий многочлен g(x). Поэтому алгоритм декодирования включает в себя деление принятого кодового слова, описываемого многочленом 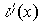 на g(x), вычисление и анализ остатка r(x). Если r(x)=0, то принятое кодовое слово считается неискаженным. Если r(x)0, то принятое кодовое слово стирается и формируется сигнал "ошибка". на g(x), вычисление и анализ остатка r(x). Если r(x)=0, то принятое кодовое слово считается неискаженным. Если r(x)0, то принятое кодовое слово стирается и формируется сигнал "ошибка".
- при кодировании способом МККТТ декодирование основано на свойстве получения определенного контрольного остатка R0
(x) при делении принятого кодового многочлена (x) на порождающий многочлен. Поэтому, если полученный при делении остаток  , то принятое кодовое слово считается неискаженным. Если остаток , то принятое кодовое слово считается неискаженным. Если остаток  , то принятое кодовое слово стирается и формируется сигнал "ошибка". Значение контрольного остатка определяется из выражения , то принятое кодовое слово стирается и формируется сигнал "ошибка". Значение контрольного остатка определяется из выражения  . .
Способы декодирования с исправлением ошибок и схемная реализация декодирующих устройств
Декодирование циклического кода в режиме исправления ошибок можно осуществлять различными способами. Ниже излагаются два способа, являющиеся наиболее простыми.
В основу первого способа положено использование таблицы синдромов (декодирования), в которой каждому многочлену или образцу ошибок ei
(x), соответствует определенный синдром Si
(x), представляющий остаток от деления принятого кодового слова 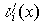 и соответствующего ему ei
(x) на g(x). Процедура декодирования следующая. Принятое кодовое слово и соответствующего ему ei
(x) на g(x). Процедура декодирования следующая. Принятое кодовое слово 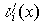 делится на g(x), определяется Si
(x) и соответствующий ему многочлен ei
(x), а затем делится на g(x), определяется Si
(x) и соответствующий ему многочлен ei
(x), а затем 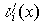 суммируется с ei
(x). В результате получаем исправленное кодовое слово, т.е. суммируется с ei
(x). В результате получаем исправленное кодовое слово, т.е.  . .
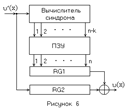
В состав декодера входят: вычислитель синдрома (ВС), два регистра сдвига RG1 и RG2, постоянное запоминающее устройство (ПЗУ), которое содержит  слова длины n, соответствующие многочленам ошибок ei
(x). слова длины n, соответствующие многочленам ошибок ei
(x).
Принятое кодовое слово 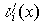 поступает на вход вычислителя синдрома, где осуществляется деление его на g(x) и формирование Si
(x), и одновременно - на вход RG2, где поступает на вход вычислителя синдрома, где осуществляется деление его на g(x) и формирование Si
(x), и одновременно - на вход RG2, где 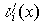 накапливается. Синдром Si
(x) используется в качестве адреса, по которому из ПЗУ в регистр RG1 записывается ei
(x), соответствующий синдрому Si
(x). Перечисленные операции завершаются за n тактов. В течение последующих n тактов происходит поэлементное суммирование содержимого RG2 и RG1, т.е. операция накапливается. Синдром Si
(x) используется в качестве адреса, по которому из ПЗУ в регистр RG1 записывается ei
(x), соответствующий синдрому Si
(x). Перечисленные операции завершаются за n тактов. В течение последующих n тактов происходит поэлементное суммирование содержимого RG2 и RG1, т.е. операция  , и исправление. ошибок. , и исправление. ошибок.
В основе второго способа исправления ошибок, позволяющего значительно сократить объем используемых табличных синдромов и существенно упростить схему декодера, лежат следующие положения:
1. Синдром Si
(x), соответствующий принятому кодовому слову равен остатку от деления 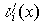 на g(x), а также остатку от деления соответствующего многочлена ошибок ei(x) на g(x), т.е. на g(x), а также остатку от деления соответствующего многочлена ошибок ei(x) на g(x), т.е.  . .
2. Если Si
(x) соответствует 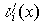 и ei
(x), то x( Si
(x) является синдромом, который соответствует и ei
(x), то x( Si
(x) является синдромом, который соответствует  и и  или или  . .
3. При исправлении ошибок используются синдромы образцов ошибок только с ненулевым коэффициентом в старшем разряде.
Поэтому при реализации этого способа множество всех образцов ошибок разбивается на классы эквивалентности. Каждый класс представляет циклический сдвиг одного образца ошибок, а синдром этого класса соответствует образцу ошибок с ненулевым старшим разрядом. Если вычисленный синдром принадлежит одному из классов эквивалентности образцов исправляемых ошибок, то старший символ кодового слова исправляется. Затем принятое слово и синдром циклически сдвигается, а процесс нахождения в предыдущей по старшинству позиции повторяется.
Для исправления ошибок, принадлежащих данному классу эквивалентности, нужно произвести n циклических сдвигов.
Простейшим является декодер Меггитта. В состав декодера входят: вычислитель синдрома, осуществляющий деление кодового слова 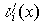 на g(x) и формирование соответствующего синдрома; блок декодеров (ДК), который настроен на синдромы всех образцов исправляемых ошибок с ненулевыми старшими разрядами; регистр сдвига RG. на g(x) и формирование соответствующего синдрома; блок декодеров (ДК), который настроен на синдромы всех образцов исправляемых ошибок с ненулевыми старшими разрядами; регистр сдвига RG.
При поступлении на вход схемы кодового слова 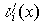 его символы заполняют регистр RG, а в вычислителе формируется соответствующий синдром Si
(x). Вычисленный синдром сравнивается со всеми табличными синдромами, заложенными в схему блока ДК, и в случае совпадения с одним из них на его выходе формируется сигнал, который исправляет ошибочный символ, находящийся в старшем разряде регистра. После этого содержимое вычислителя и RG циклически сдвигается на один шаг. Этот сдвиг реализует операции его символы заполняют регистр RG, а в вычислителе формируется соответствующий синдром Si
(x). Вычисленный синдром сравнивается со всеми табличными синдромами, заложенными в схему блока ДК, и в случае совпадения с одним из них на его выходе формируется сигнал, который исправляет ошибочный символ, находящийся в старшем разряде регистра. После этого содержимое вычислителя и RG циклически сдвигается на один шаг. Этот сдвиг реализует операции 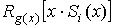 и и  . Если новый синдром совпадает с одним из табличных синдромов, то это означает, что произошла ошибка во втором по старшинству символе кодового слова, который, перейдя в старший разряд RG, исправляется. Затем производится новый циклический сдвиг на одну позицию и новая проверка на совпадение синдромов. После повторения этого процесса n раз в RG будет сформировано исправленное кодовое слово. Введение обратной связи для RG не обязательно, так как в процессе исправления ошибок символы кодового слова поступают на выход декодера. . Если новый синдром совпадает с одним из табличных синдромов, то это означает, что произошла ошибка во втором по старшинству символе кодового слова, который, перейдя в старший разряд RG, исправляется. Затем производится новый циклический сдвиг на одну позицию и новая проверка на совпадение синдромов. После повторения этого процесса n раз в RG будет сформировано исправленное кодовое слово. Введение обратной связи для RG не обязательно, так как в процессе исправления ошибок символы кодового слова поступают на выход декодера.
Пример.
Рассмотрим схему и работу декодера Меггитта циклического (15,7)-кода, обеспечивающего исправление одиночных и двойных ошибок, с g(x)=x8
+ x7
+ x6
+ x4
+1 (см. рисунок 1).


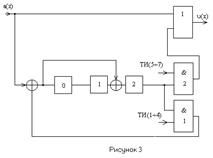

Блок декодеров настраивается на 15 синдромов, которые представлены в таблице 1 и соответствуют классам эквивалентности с образцами ошибок в старшем разряде.
| Таблица 1 |
| №
|
| е(х)
|
S(x)
|
№
|
е(х)
|
S(x)
|
| 1 |
x14
|
x7
+ x6
+x5
+ x3
|
9 |
x14
+ x6
|
| 2 |
x14
+ x13
|
x7
+ x4
+x3
+ x2
|
10 |
x14
+ x5
|
x7
+ x6
+x3
|
| 3 |
x14
+ x12
|
x7
+ x6
+x4
+ x |
11 |
x14
+ x4
|
x7
+ x6
+x5
+ x4
+x3
|
| 4 |
x14
+ x11
|
12 |
x14
+ x3
|
x7
+ x6
+x5
|
| 5 |
x14
+ x10
|
13 |
x14
+ x2
|
x7
+ x6
+x5
+ x3
+x2
|
| 6 |
x14
+ x9
|
14 |
x14
+ x1
|
x7
+ x6
+x5
+ x3
+x |
| 7 |
x14
+ x8
|
15 |
x14
+ x0
|
x7
+ x6
+x5
+ x3
+0 |
| 8 |
x14
+ x7
|
Допустим, что ошибки в 3 и 5 разрядах, т.е. им соответствует многочлен ошибки e(x)=x12
+x10
.
При поступлении на вход декодера искаженного кодового слова он заполняет регистр и в вычислителе формируется синдром 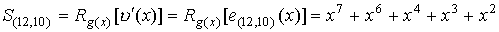 . .
Блок декодеров не реагирует на этот синдром.
Затем происходит сдвиг кодового слова в RG, а в BC формируется новый синдром  . .
Блок декодеров и в этом случае не срабатывает.
При следующем сдвиге кодового слова в RG первый искаженный разряд занимает старшую позицию в RG, а в BC формируется синдром  , от которого срабатывает БДК. В результате исправляется первая ошибка. , от которого срабатывает БДК. В результате исправляется первая ошибка.
Следующим сдвиг приводит к формированию синдрома  . .
Этот синдром соответствует многочлену ошибки e(x)=x13
+x0
, т.к. первый искаженный разряд по обратной связи должен занять младшую позицию RG.
На синдром S(13,0)
блок декодеров не реагирует.
При следующем сдвиге кодового слова в RG второй искаженный разряд занимает старшую позицию в RG, а в BC формируется синдром 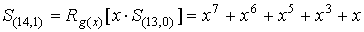 , от которого срабатывает БДК. В результате исправляется вторая ошибка в кодовом слове. , от которого срабатывает БДК. В результате исправляется вторая ошибка в кодовом слове.
Коды Рида-Соломона (РС)
Коды РС являются недвоичными циклическими кодами, символы кодовых слов которых берутся из конечного поля GF(q). Здесь q степень некоторого простого числа, например q=2m
.
Допустим, что РС-код построен над GF(8), которое является расширением поля GF(2) по модулю примитивного многочлена f(z)=z3
+z+1. В этом случае символы кодовых слов кода будут иметь значения, представленные в таблице 2.
| Таблица 2 |
| 000 |
0 |
0 |
011 |
z+1 |
3
|
| 001 |
1 |
0
|
110 |
z2
+z |
4
|
| 010 |
z |
1
|
111 |
z2
+z+1 |
5
|
| 100 |
z2
|
2
|
101 |
z2
+1 |
6
|
Кодовые слова РС-кода отображаются в виде многочленов
 , ,
где N - длина кода; Vi
- q-ичные коэффициенты (символы кодовых слов), которые могут принимать любое значение из GF(q).
Эти коэффициенты как это следует из таблицы, также отображаются многочленами с двоичными коэффициентами  . Коды РС являются максимальными, т.к. при длине кода N и информационной последовательности k они обладают наибольшим кодовым расстоянием d=N-k+1. . Коды РС являются максимальными, т.к. при длине кода N и информационной последовательности k они обладают наибольшим кодовым расстоянием d=N-k+1.
Порождающим многочленом g(x) РС-кода является делитель двучлена xN
+1 степени меньшей N с коэффициентами из GF(q) при условии, что элементы 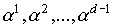 этого поля являются корнями g(x). Здесь этого поля являются корнями g(x). Здесь 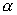 - примитивный элемент GF(q). - примитивный элемент GF(q).
На основе этого определения, а также теоремы Безу, выражение для порождающего многочлена РС-кода будет иметь вид  . .
Степень g(x) равна d-1=N-k=R.
В РС-кодах принадлежность кодовых слов данному коду определяется выполнением d-1 уравнений в соответствии с выражением 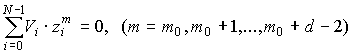 (*), где Vi
- символы-коэффициенты из GF(q); z0
, z1
... zN-1
- ненулевые элементы GF(q). (*), где Vi
- символы-коэффициенты из GF(q); z0
, z1
... zN-1
- ненулевые элементы GF(q).
Элементы z0
, z1
... zN-1
называются локаторами, т.е. указывающими на номер позиции символа кодового слова.
Например, указателем i - позиции является локатор zi или элемент i
GF(q).
Так как все локаторы должны быть различны и причем ненулевыми, то их число в GF(q) равно q-1. Следовательно, такое количество символов должно быть в кодовых словах кода.Поэтому обычно длина РС-кода определяется из выражения N=q-1.
Пример.
Допустим, что длина РС-кода равна N, кодовое расстояние d=3, то в соответствии с (*) проверочными уравнениями будут

Свойства РС-кодов.
1. Циклический сдвиг кодовых слов, символы которых принимают значение из GF(q), порождает новые кодовые слова этого же кода.
2. Сумма по mod2 двух и более кодовых слов дает кодовое слово, принадлежащее этому же коду.
3. Кодовое расстояние РС-кода определяется не по двоичным элементам, а по q-ичным символам.
4. В РС-коде, исправляющем tu
ошибок порождающий многочлен определяется из выражения  . Обычно m0
принимают равным 1. Однако, с помощью разумного выбора значения m0
, иногда можно упростить схему кодера. . Обычно m0
принимают равным 1. Однако, с помощью разумного выбора значения m0
, иногда можно упростить схему кодера.
5. Корректирующие способности РС-кода определяются его кодовым расстоянием.

где T0
и Tu
- длина пакетов, в которых обнаруживаются и исправляются ошибки.
Обнаружение ошибок в кодовых словах состоит в проверке условий ((), т.е. определении синдрома  , элементы которого определяются из выражения , элементы которого определяются из выражения  . .
Пример.
Требуется сформировать кодовое слово РС-кода над GF(23
), соответствующее двоичной информационной последовательности a(1,0)=000000011100101.
Так как m=3, то каждый q-ичный символ кода состоит из трех двоичных элементов. Поэтому с учетом таблицы 6 a(x)=3
x2
+ 2
x+6
.
Определяем параметры кода. N=q-1=7; k=5; R=2; d=N-k+1=3;
 . .
Кодовое слово формируется в соответствии с выражением.  , ,
где  . . 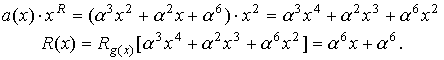
В результате 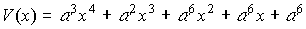 или в двоичной форме V(1,0)=000.000.011.100.101.101.101. или в двоичной форме V(1,0)=000.000.011.100.101.101.101.
ЛИТЕРАТУРА
1. Лидовский В.И. Теория информации. - М., «Высшая школа», 2002г. – 120с.
2. Метрология и радиоизмерения в телекоммуникационных системах. Учебник для ВУЗов. / В.И.Нефедов, В.И.Халкин, Е.В.Федоров и др. – М.: Высшая школа, 2001 г. – 383с.
3. Цапенко М.П. Измерительные информационные системы. - . – М.: Энергоатом издат, 2005. - 440с.
4. Зюко А.Г. , Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. М: Радио и связь, 2001 г. –368 с.
5. Б. Скляр. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. – М.: Издательский дом «Вильямс», 2003 г. – 1104 с.
|