Министерство образования РФ.
Новгородский Государственный Университет им. Ярослава Мудрого.
Кафедра ОиЭФ.
“Особенности работы счетчиков излучения”
Курсовая работа по учебной дисциплине:
“Прикладная физика”
Руководитель:
проф. Кафедры ОиЭФ
д.ф.- м.н.
Данильчук Л.Н.
Выполнили:
студенты ФТФ группы 8121
Круглова Е.А.
и Удальцов Я.М.
Великий Новгород
2002 год.
Содержание
I. Радиоактивные излучения и их свойства
II. Основной закон радиоактивного распада. Единицы измерения радиоактивности
III. Физическая доза излучения, мощность физической дозы и единицы их измерения
IV. Газоразрядные счётчики ионизирующих частиц
V. Счётчик Гейгера с высоковольтным питанием от преобразователя постоянного напряжения на полупроводниковом триоде
VI. Счётчик СТС-5
VII. Схема удвоения напряжения
VIII. Счётчик слабого бета- излучения СТБ-13
IX. Разработка микросхемы для счётчика слабого бета-излучения
X. Применение счётчика
I РАДИОАКТИВНЫЕ ИЗЛУЧЕНИЯ И ИХ СВОЙСТВА
Радиоактивные распады ядер неустойчивых изотопов химических элементов принято определять по виду создаваемых ими излучений. К основным видам радиоактивного распада относятся альфа-распад и бета-распад.
Альфа-распад сопровождается вылетом из ядра альфа-частицы, представляющей собой быстролетящее ядро изотопа гелия Нe(А=4,Z=2). Радиоактивные вещества, обладающие альфа- распадом, принято называть альфа- активными веществами.
Бета-распад сопровождается вылетом из ядра бета-частицы, представляющей собой электрон или позитрон.
Позитроны — элементарные частицы, обладающие массой электрона и имеющие положительный заряд, по абсолютной величине равный заряду электрона. Вещества, создающие бета-излучение, принято называть бета- активными.
В большинстве случаев после вылета бета- или альфа-частицы ядро нового атома остается в возбужденном состоянии, иначе говоря, оно обладает избытком энергии. Избыточная энергия возбужденного ядра излучается в виде кванта (порции) электромагнитной энергии, получившей название гамма- кванта.
Радиоактивные изотопы, у которых бета-распад сопровождается излучением гамма- квантов, принято называть бета-, гамма- активными.
Альфа-излучение. Альфа- активные изотопы относятся к тяжелым элементам с порядковым номером больше атомного номера свинца (Z>82). Неустойчивость ядер таких элементов может быть объяснена чрезмерно большим числом протонов в ядре, взаимное электростатическое отталкивание между которыми ослабляет действие особых ядерных сил притяжения между протонами и нейтронами, обуславливающих прочность ядра.
При испускании альфа-частицы исходный атом превращаетсяв новый атом с уменьшенным на 2 единицы зарядом (Z) и на 4 единицы Рис. 1 График распада массовым числом (А). Так, например, атомы изотопа плутония-239 альфа- активного изотопа- путем альфа - распада превращаются в атомы изотопа урана-235. плутония-239 (Pu )
Схему распада можно представить символами элементов следующим образом:

Распад радиоактивных ядер удобно изображать также графиком (рис.1), в котором каждому энергетическому состоянию ядра (исходного и вновь образованного) соответствует горизонтальная линия, а переход из одного энергетического состояния в другое (т. е. распад) изображается в виде стрелки.

Направление стрелки соответствует направлению изменения порядкового номера изотопа (Z) при распаде. При альфа- распаде порядковый номер элемента уменьшается на 2, поэтому стрелка на рис. 1 имеет направление влево.
На таком графике указываются обычно энергия частиц, излучаемых при распаде, и другие данные, характеризующие свойства изотопов.
Альфа-частицы, испускаемые ядрами одного изотопа, имеют равные энергии. Большинство альфа-активных изотопов излучает частицы с начальными энергиями в пределах от 4 до 8 Мэв, что соответствует начальной скорости их движения порядка 109 — 2 • 109 см/сек (скорость распространения света составляет 3∙1010 см/сек). Проходя через вещество, альфа-частицы, обладающие относительно большим электрическим зарядом (Z=2), эффективно взаимодействуют с электронами, вызывая ионизацию и возбуждение атомов и молекул среды. Хотя в каждом акте взаимодействия с электронами расходуется лишь небольшая доля начальной энергии альфа-частиц, однако большое число актов взаимодействия на единице пути пробега обуславливает быстрое замедление альфа-частицы и сравнительно короткий путь пробега. Таким образом, альфа-излучение, т. е. поток альфа-частиц, обладает высокой ионизирующей и малой проникающей способностью.
Ионизирующая способность радиоактивных излучений характеризуется плотностью ионизации, т. е. числом пар ионов, создаваемым на 1 см пути в поглощающей среде. Плотность ионизации зависит от энергий альфа-частицы и свойств среды. На рис. 2 приведена зависимость плотности ионизации, создаваемой альфа-частицей с начальной энергией Е = 7 Мэв в воздухе, от пройденного пути. На протяжении большей части пути плотность ионизации практически постоянна, однако в конце его, когда энергия частицы и скорость ее движения уменьшаются, ионизирующая способность увеличивается. Средняя плотность ионизации воздуха альфа-частицей имеет величину 30000 пар ионов на 1 см пути.
Общее число пар ионов, создаваемых альфа-частицей до полной ее остановки, зависит от начальной энергии частицы и средней работы, затрачиваемой на образование одной пары ионов. Так, например, при средней работе образования одной пары ионов в воздухе, равной приблизительно 33 эй, альфа-частица с начальной энергией Е = 5 Мэв = 5 000 000 эВ создаст в воздухе (5000000/33)=150000 пар ионов и будет иметь длину пробега порядка (150000/30000)=5cм.
С увеличением плотности среды увеличивается число атомов и электронов в единице объема, поэтому плотность ионизации альфа-частицей возрастает, а длина пробега частиц уменьшается. Так, в алюминии альфа-частицы с энергией 7 Мэв имеют длину пробега порядка 0,0041 мм (4,1 микрона). Обычная тонкая бумага полностью поглощает альфа-частицы естественных альфа- активных изотопов.
Бета-излучение. Источниками бета - излучения является подавляющее большинство радиоактивных изотопов. Образование бета-частицы при радиоактивном распаде происходит за счет превращения одного из нейтронов ядра в протон (электронный бета-распад) или протона к нейтрону (позитронный бета-распад). При бета-распаде массовое число атома (А) не изменяется, так как общее число нуклонов (т. е. протонов и нейтронов) остается в ядре неизменным; заряд ядра увеличивается на единицу при электронном распаде и уменьшается на единицу при позитронном распаде. Примеры электронного и позитронного бета-распадов приведены на рис. 3.
 |
Характерным для бета-распада является то, что ядра одного и того же радиоактивного изотопа испускают бета-частицы с различными начальными энергиями. Наибольшее значение начальной энергии бета-частиц для каждого радиоактивного изотопа имеет строго определенную величину и называется максимальной энергией бета- излучения (Eβ max). У большинства радиоактивных изотопов максимальная энергия бета-излучения имеет величину в пределах от нескольких десятков килоэлектронвольт до 3 Мэв.
Бета-излучение с максимальной энергией меньше 0,5 Мэв условно считается «мягким»; чем больше энергия, тем более «жестким» считается излучение.
Типовое распределение частиц по энергиям для бета-излучения (энергетический спектр) приведено на рис. 4. Средняя энергия бета-частиц обычно составляет ⅓ максимальной. Прохождение бета-частиц через вещество сопровождается их взаимодействием с электронами оболочек атома и ядрами. Это взаимодействие, так же как и у альфа-частиц, имеет электрическую природу, а сопровождается, в зависимости от переданной энергии, либо ионизацией молекул и атомов среды, либо их возбуждением. Общее число пар ионов, которое создается одной бета-частицей в облучаемой среде, определяется ее начальной энергией и средней работой, затрачиваемой на образование пары ионов в облучаемой среде (33 эВ для воздуха). Чем больше начальная энергия бета-частиц, тем большее число, пар ионов она образует на всем своем пути пролета в облучаемой среде.
Бета-частицы обладают значительно меньшей по сравнению с альфа-частицей ионизирующей способностью; средняя плотность ионизации бета-частицей в воздухе составляет около 100 пар ионов на 1 см пути. Меньшая ионизирующая способность бета-частицы объясняется меньшей величиной ее электрического заряда и значительно большими скоростями движения. Так же как и для альфа-частиц, плотность ионизации бета-частицами возрастает с уменьшением их скорости, т. е. к концу пролета бета-частиц.
Имея малую массу, бета-частицы значительно изменяют направление своего движения при случайном попадании в поле действия электрических сил ядра. Поэтому траектория движения бета-частиц в облучаемой среде представляет ломаную линию, а длина пробега бета-частиц по направлению первоначального движения значительно меньше истинного ее пути. При прохождении бета-излучения через слой вещества число бета-частиц постепенно уменьшается (рис.5). Последнее объясняется тем, что длина пробега бета-частицы в среде зависит от ее начальной энергии, а бета-излучение содержит частицы с широким спектром начальных энергий от близких к нулевой до Е max.
Максимальный пробег бета-частиц в среде Rmax определяется глубиной проникновения в нее бета-частиц с максимальной начальной энергией. Величина максимального пробега бета-частиц различных изотопов различна и может быть рассчитана по формулам;
где Eβ max - максимальная энергия бета- излучения изотопов в Мэв;
ρ - плотность поглощающей среды в г/см3;
Rmax - максимальная длина пробега в см.
Так, например, в воздухе (ρ = 0,00129 г/см3) бета- излучение с Eβ max = 1 Мэв имеет максимальный пробег порядка 3 м, а с энергией 3 Мэв— 11,5 м. в алюминии (ρ = 2,7 г/см) при тех же максимальных энергиях бета- излучения максимальный пробег примерно в 2000 раз меньше и составляет 1,6 и 5,5 м соответственно.
Приведенный пример показывает, что проникающая способность бета-частиц значительно больше проникающей способности альфа-частиц. Однако по абсолютному значению она невелика, поэтому защита от бета- излучения относительно проста. Необходимый для защиты слой вещества можно определить по приведенным выше формулам.
Отличительной особенностью позитронного бета- излучения является короткий промежуток существования позитрона. В конце своего пробега замедленный позитрон при взаимодействии с одним из электронов среды преобразуется в два гамма- кванта с энергией 0,51 МэВ каждый. Такое преобразование массы частиц в электромагнитную энергию называется реакцией анигиляции; оно доказывает единство материи и энергии.
Таким образом, позитронный бета-распад всегда приводит к появлению гамма-излучения.
Гамма-излучение. Гамма-излучение представляет собой поток квантов электромагнитной энергии, испускаемых возбужденными ядрами радиоактивных элементов после бета- или альфа- распада.
Примеры схем радиоактивного распада ядер, сопровождающихся излучением гамма- квантов, приведены па рис. 6
Каждый радиоактивный изотоп излучает гамма- кванты определенной энергии и в определенном количественном отношении к общему числу распадов. Так, радиоактивный кобальт-60 создает два гамма-кванта при каждом бета-распаде ядра, а у радиоактивного радня-226 излучение гамма-кванта наблюдается примерно в шести случаях из 100 распадающихся атомов.
По своей природе и свойствам гамма-излучение не отличается от рентгеновского. Обычно под термином рентгеновских лучей подразумевают излучения, создаваемые электронной оболочкой атома при его переходе из возбужденного состояния в нормальное или в результате торможения быстрых электронов, попадающих в поле действия электрических сил ядра (тормозное рентгеновское излучение); в отличие от этого гамма-кванты являются излучениями возбужденного ядра.
Энергия гамма-квантов, излучаемых различными радиоактивными изотопами, лежит в пределах от сотых долей до нескольких мегаэлектронвольт.
Гамма-излучение в окружающем пространстве распространяется со скоростью света (3- 10'° см/сек) и обладает высокой проникающей способностью.
Отсутствие массы покоя и электрического заряда у квантов гамма-излучения обуславливает особенности характера взаимодействия их с веществом.
К основным видам взаимодействия гамма-квантов с веществом относятся: фотоэлектрическое поглощение гамма-квантов, комптоновский эффект (или рассеяние гамма-квантов) и образование электронно-позитронных пар. Условное схематическое изображение видов взаимодействия гамма-кванта с атомом и его электронами приведено на рис. 7.
При фотоэлектрическом поглощении гамма-квант полностью поглощается атомом вещества, в результате чего из атома вылетает электрон. Энергия гамма-кванта при этом процессе расходуется: небольшая часть — на отрыв электрона с его оболочки, а остальная часть — на сообщение ему начальной скорости.
Вырванный электрон (фотоэлектрон) движется под некоторым квантов с атомами и электронами углом к первоначальному направлению движения гамма-кванта и, подобно бета-частице, ионизирует атомы и молекулы окружающей среды.
Фотоэффект является преобладающим видом взаимодействия гамма-излучения с веществом при малой энергии квантов— меньше 0,1—0,5 Мэв. Нижняя граница соответствует средам с малым порядковым номером образующих элементов (воздух, ткани живых организмов, пластмассы и т. д.), верхняя — для веществ с большим порядковым номером элементов (железо, свинец и т. д.).
При комптоновском эффекте гамма-квант, взаимодействуя с электроном атома, передает ему только часть энергии; при этом квант с уменьшенной энергией отклоняется от первоначального направления движения (рассеивается). Чем больше энергии передается электрону, тем больше отклоняется от первоначального направления (рассеивается) квант.
Рассеяние гамма-квантов происходит многократно и в конце концов заканчивается фотоэлектрическим поглощением.
Поток рассеянных гамма-квантов образует так называемое рассеянное излучение, которое не имеет резко выраженной направленности распространения, свойственной гамма-излучению. Электрон при комптоновском эффекте, названный комптоновским, вылетает из атома также под некоторым углом к первоначальному движению гамма-кванта и расходует свою энергию на ионизацию и возбуждение молекул окружающей среды. Таким образом, особенностью комптоновского эффекта является наличие двух процессов: поглощение энергии гамма-излучения путем передачи ее электронам и рассеяние гамма-квантов.
Комптоновский эффект является преобладающим видом взаимодействия для широкого диапазона средних энергий гамма-квантов: для воздуха в диапазоне энергий от 0,1 до 20 Мэв; для свинца примерно от 0,5 до 5 Мэв.
Эффект образования электронно-позитронных пар наблюдается при попадании гамма-квантов с энергией больше 1,02 Мэв в сильное электрическое поле ядра атома вещества. В результате такого взаимодействия энергия гамма-кванта расходуется на образование массы электрона и позитрона (по 0,51 Мэв), а также на сообщение им начальной скорости движения.
При движении в среде электрон и позитрон расходуют свою кинетическую энергию на ионизацию и возбуждение атомов и молекул среды; когда позитрон уменьшит скорость своего движения, он взаимодействует с одним из свободных электронов среды, в результате чего образуются два гамма-кванта.
Эффект образования пар играет существенную роль в поглощении энергии гамма-излучения в веществах с большим порядковым номером образующих элементов и при большой энергия гамма-квантов.
Перечисленные виды взаимодействия обуславливают постепенное ослабление интенсивности гамма-излучения по мере увеличения толщины слоя вещества. Интенсивностью гамма-излучения называется энергия, которая переносится в единицу времени (обычно в секунду) потоком гамма-квантов, проходящим через 1 см поверхности, расположенной перпендикулярно к направлению их движения. Если гамма-излучение содержит гамма-кванты с одинаковой энергией, то оно называется монохроматическим. Интенсивность монохроматического гамма-излучения I равна произведению энергии гамма-квантов Е на их число, проходящее через 1 см поверхности в секунду, п:
Ослабление параллельного пучка гамма-излучения происходит по экспоненциальному закону, графически изображенному на рис. 8, и может быть выражено следующими формулами:
где I0 — интенсивность гамма-излучения при входе в поглощающую среду;
I — интенсивность гамма-излучения после прохождения слоя толщиной в см;
d — слой половинного ослабления, т. е. толщина слоя данного материала, обеспечивающая ослабление интенсивности узкого пучка гамма-излучения в два раза;
µ —линейный коэффициент ослабления гамма-излучения, показывающий, какая доля гамма-квантов из общего их числа будет иметь акты взаимодействия на пути в 1 см.
Линейный коэффициент и слой половинного ослабления в связаны между собой соотношением
Ослабление интенсивности гамма-излучения обусловлено всеми тремя видами взаимодействия гамма-квантов со средой. Поэтому величина µ складывается из коэффициента поглощения за счет фотоэффекта (τ ), коэффициента поглощения за счет образования пар (χ) и коэффициента комптоновского ослабления (σ), который в свою очередь целесообразно разбить на коэффициент поглощения (σa ) и коэффициент рассеяния (σs );
Сумму первых трех слагающих в этом выражении, определяющих поглощение энергии гамма-квантов, принято называть линейным коэффициентом поглощения:

Можно показать, что для параллельного пучка монохроматического гамма-излучения произведение интенсивности на коэффициент поглощения равно энергии, поглощенной единицей объема облучаемой среды в единицу времени (секунду):
В дозиметрии эта величина носит название мощности дозы излучения (или облучения) и обозначается Pγ
Величина линейных коэффициентов ослабления и поглощения зависит, с одной стороны, от свойств поглощающей среды (от плотности вещества и порядкового номера элементов Z) и. с другой стороны, от энергии квантов гамма-излучения. Коэффициенты µ и µa , увеличиваются пропорционально плотности вещества ρ. а зависимость от Z элементов вещества и энергии гамма-квантов весьма сложная и обычно дается для различных веществ в виде таблиц или графиков. В приложении 2 приведена сокращенная таблица величин половинного слоя ослабления в , линейного коэффициента ослабления µ и поглощения µa для воздуха, тканей животных (мышц), железа и свинца, для энергии гамма-квантов в диапазоне 0,1 — 2,5 Мэв.
Если вещества имеют примерно равный средний порядковый номер элементов, из которых они образованы, то они обладают также одинаковой закономерностью изменения от энергии гамма-квантов и равным количеством энергии, поглощаемой единицей массы вещества (граммом). Так, например, воздух (Zcp,= 7,64), ткани живого организма (Zcp =7,5) и многие органические пластмассы имеют примерно равное Zcp. Все эти вещества являются эквивалентными по свойствам поглощения энергии гамма-излучения и обычно называются «воздухо- эквивалентными». Для этих веществ имеет место соотношение
которое показывает, что их коэффициенты поглощения на единицу массы, носящие название массового поглощения , примерно равны между собой при всех энергиях гамма-квантов. Подобного соотношения нет для веществ с резко различными Zcp, в чем можно убедиться, ознакомившись с таблицей, в которой приведены массовые коэффициенты поглощения для воздуха и свинца при различных энергиях гамма-квантов:
Энергия, поглощенная средой при воздействии на нее гамма-излучения, в конечном итоге расходуется на ионизацию и возбуждение атомов и молекул среды. Однако эта ионизация создается не самими гамма-квантами, а теми вторичными электронами, которые образуются в результате рассмотренных актов взаимодействия гамма-квантов с атомами среды. При этом средняя работа образования одной пары ионов в воздухе такая же, как и для бета-излучения ( ε = 33 эв).
Гамма-излучение, в отличие от альфа- и бета-излучений, не имеет строго определенного слоя полного ослабления. Теоретически полное ослабление гамма-излучения будет происходить при бесконечно толстом слое вещества. Для практической оценки проникающей способности гамма-излучения считается, что средняя длина пробега гамма-квантов соответствует слою вещества, обеспечивающему ослабление гамма-излучения в 2,718 раза. Величина среднего пробега R гамма-квантов определяется формулой
и для гамма-квантов с Eγ = 1 Мэв в воздухе составляет 120 м.
Средняя плотность ионизации в воздухе для гамма-квантов с той же энергией будет иметь величину
Таким образом, обладая большей проникающей способностью, гамма-излучение имеет меньшую ионизирующую способность. Однако большая проникающая способность создает условие облучения от удаленных источников и поэтому на участках местности, зараженных радиоактивными веществами, гамма-излучение является наиболее опасным видом радиоактивного излучения с точки зрения поражения человека при внешнем облучении.
II. ОСНОВНОЙ ЗАКОН РАДИОАКТИВНОГО РАСПАДА. ЕДИНИЦЫ ИЗМЕРЕНИЯ РАДИОАКТИВНОСТИ
Каждый радиоактивный атом рано или поздно претерпевает превращение, однако предугадать момент распада данного атома радиоактивного изотопа невозможно.
Вместе с тем при наличии достаточно большого числа атомов N какого-либо радиоактивного изотопа закономерность радиоактивного распада можно установить экспериментально. Закон, по которому уменьшается число радиоактивных атомов, можно сформулировать в следующей простой форме: половина любого достаточно большого количества атомов радиоактивного изотопа распадается за равные промежутки времени.
Этот промежуток времени называется периодом полураспада Т и является одной из основных характеристик радиоактивного изотопа.
Период полураспада известных радиоактивных изотопов колеблется от ничтожно малых долей секунды до многих миллиардов лет. Так, например, период полураспада ура-на-238 составляет 4,5 миллиарда лет, радия-226 - 1590 лет, стронция-90 — 19.9 года, кобальта-60 — 5,3 года, строя-цня-89 — 53 дня.
Зная период полураспада радиоактивного изотопа, нетрудно определить число не распавшихся атомов для любого момента времени по формуле:
Кривая радиоактивного распада, построенная по этой формуле, приведена на рис. 9. Она пригодна для любого изотопа, если число атомов и время выражать соответственно в долях от первоначального количества атомов и в периодах полураспада.

Рис. 9 Закон радиоактивного распада, где N0— первоначальное количество атомов радиоактивного изотопа; N— число не распавшихся атомов; t— время, прошедшее с момента, когда число атомов равнялось No.
В более удобном для математического анализа виде закон радиоактивного распада выражается формулой
где — постоянная распада, показывающая долю атомов, распадающихся за единицу времени;
е— основание натуральных логарифмов, равное 2,718,
Среднее число атомов, распадающееся в единицу времени (т. е. скорость распада), называется активностью радиоактивного вещества.
Активность (а) является количественной характеристикой источников радиоактивных излучений, зависящей от числа радиоактивных атомов и периода их полураспада:
Чем больше период полураспада, тем меньшей активностью обладает данное количество радиоактивных атомов.
Активность, так же как и количество радиоактивных атомов, уменьшается с течением времени по экспоненциальному закону:
Измерение активности числом распадающихся атомов в единицу времени (минуту, секунду) обычно используется только для ничтожно малых количеств радиоактивных веществ (например, для характеристики зараженности радиоактивными веществами поверхностей различных объектов и предметов).
Для измерения активности международным соглашением принята более крупная единица, названная кюри.
Кюри соответствует активности такого количества радиоактивного вещества, в котором за 1 секунду происходит 37 миллиардов распадов (1 кюри = 3,7 • 10'° расп/сек).
Кюри относительно большая единица активности. Более мелкими единицами являются производные от кюри:
Следует иметь в виду, что активность как характеристика радиоактивного источника определяет только количественную сторону явления радиоактивности. Знание величины активности источника еще недостаточно для наиболее полной оценки его свойств, так как неизвестными остаются такие важнейшие характеристики распада, как виды излучения, число и энергия излучаемых частиц и квантов. Эти характеристики полностью можно установить, если известны количество и типы радиоактивных изотопов, входящих в состав данного источника.
Измерение активности обычно производится путем регистрации (счета) полного числа или части частиц, излучаемых источником в единицу времени. Если при измерении активности использовался прибор, способный регистрировать альфа-частицы и не регистрирующий бета-частицы и гамма- кванты, то можно говорить об альфа- активности источника. Соответственно, если в процессе измерения активности регистрируются только бета-частицы, то результат измерения определяет бета-активность источника.
Активность источников гамма-излучения часто выражается не в кюри или милликюри, а специальными единицами измерения — грамм-эквивалентами радия, миллиграмм-эквивалентами радия или микрограмм-эквивалентами радия.
Источник, обладающий активностью в 1 грамм-эквивалент радия, создает на данном расстоянии от него такой же ионизационный эффект в воздухе за счет гамма-излучения, который создает гамма-излучение одного грамма радия, находящегося в равновесии с продуктами своего распада, на том же расстоянии.
III. ФИЗИЧЕСКАЯ ДОЗА ИЗЛУЧЕНИЯ, МОЩНОСТЬ ФИЗИЧЕСКОЙ ДОЗЫ И ЕДИНИЦЫ ИХ ИЗМЕРЕНИЯ
Физической дозой или, кратко, дозой излучения называется количество энергии, поглощенное единицей объема облучаемой среды за все время облучения.
Понятие о физической дозе впервые было введено для характеристики количества рентгеновского излучения с целью дозирования облучения. Физическая доза характеризует поражающее действие ионизирующих излучений на живые организмы, поэтому это понятие использовано и для характеристики радиоактивных излучений. Величина дозы излучений оценивается по эффекту ионизации в воздухе. Это объясняется тем, что ионизация воздуха поддастся достаточно точному измерению. Кроме того, ткани животных являются воздухоэквивалентными по поглощению рентгеновских и гамма-излучений, поэтому поглощаемая 1 см³ ткани энергия излучения пропорциональна дозе, измеренной в воздухе. Таким образом, по дозе, измеренной в воздухе, можно оценивать поражающее действие излучений на живые организмы.
В качестве единицы измерения дозы принята международная единица — рентген.
Рентген (р) — это такая доза рентгеновского или гамма-излучения, при которой в 0,001293 г сухого воздуха (т. е. в 1 см3 воздуха при 0°С и нормальном атмосферном давлении) образуется 2,08 • 10 пар ионов, обладающих одной электростатической единицей заряда каждого знака. Более мелкими единицами для измерения дозы являются миллирентген (мр) и микрорентген (мкр).
Средняя работа, затрачиваемая гамма-излучением на образование одной пары ионов в воздухе, составляет 33 эВ, поэтому дозе 1 р соответствует энергия, поглощенная в 1 см3, Wвозд =2,08 109 33 = 68,64 10 эВ или (умножая на 1,6 • 10 для перевода в эрги) Wвозд = 0,11 эрг.
При дозе 1 р в воздухе энергия, поглощаемая в 1 см живой ткани, составляет
Единицу измерения дозы — рентген можно использовать также для характеристики дозы бета- и альфа-излучений.
Дозу бета- и альфа-излучений, которая создает в единице объема воздуха такое же количество пар ионов, как и доза 1 р гамма-излучения, принято называть физическим эквивалентом рентгена (фэр).
Так как биологическое действие на живые организмы различных излучений не одинаково, было введено понятие биологического эквивалента рентгена. Биологический эквивалент рентгена (бэр) — это такая доза альфа-, бета- или нейтронного излучения, которая эквивалентна по биологическому действию на живой организм одному рентгену гамма-излучения. При непосредственном облучении тканей живых организмов 1 р гамма-излучения соответствует 1 фэр бета-излучения и 0,1 фэр альфа-излучения. Это соответствие установлено в результате длительных наблюдений и многочисленных опытов.
Физическая доза излучения (или облучения) характеризует поглощенную энергию независимо от времени облучения. Например, дозу в 10 р можно получить за 1 час, за . 100 дней или за какой-либо другой промежуток времени. Для характеристики скорости нарастания дозы во времени
введено понятие мощности физической дозы {сокращенно — мощность дозы). Мощностью дозы (Р) называется энергия, поглощаемая единицей объема облучаемой среды в единицу времени. Единицами измерения мощности дозы являются рентген в час (р/час) , миллирентген в час (мр/час), микрорентген в секунду (мкр/сек) и др.
Мощность дозы зависит от интенсивности излучения; для монохроматического гамма-излучения эта связь определяется соотношением
где Iγ - интенсивность излучения;
µa - линейный коэффициент поглощения гамма-лучей в веществе, подвергающемся облучению;
n - число гамма-квантов, проходящих через 1 см3 облучаемой среды в 1 сек.;
Еγ - энергия одного гамма-кванта.
Если интенсивность излучения постоянная, то мощность дозы соответствует дозе облучения за единицу времени. В этом случае дозу облучения Dγ за любой другой промежуток времени ∆t можно рассчитать по формуле

В этой формуле поэтому

Полученное выражение показывает, что доза облучения зависит от числа гамма-квантов (Zγ ), проходящих через объем в 1 см3 облучаемой среды за все время облучения ( ∆t), а также от их энергии (Eγµa ).
IV. ГАЗОРАЗРЯДНЫЕ СЧЕТЧИКИ ИОНИЗИРУЮЩИХ ЧАСТИЦ
Более эффективными для регистрации радиоактивных частиц являются газоразрядные счетчики. Для увеличения импульсов в газовых счетчиках используется ударная ионизация атомов газа электронами, ускоренными сильным электрическим полем.
Газоразрядный (сокращенно — газовый) счетчик, так же как и ионизационная камера, представляет собой конденсатор с газовым наполнением пространства между электродами.
В большинстве случаев счетчики конструктивно выполняются в виде закрытого металлического или стеклянного •цилиндра, покрытого внутри слоем металла; по оси цилиндра натягивается тонкая нить (рис. 10). Металлический цилиндр используется в качестве катода, т. е. к нему подводится проводник от отрицательного зажима источника напряжения. Нить является анодом счетчика; через сопротивление нагрузки она соединяется с положительным зажимом источника напряжения. Газовые счетчики наполняются обычно смесью инертных газов — неона (Ne) и аргона (Аг) при пониженном давлении 100—200 мм ртутного столби.
Рис. 10 Устройство газового счетчика с металлическим корпусом и схема включенияУказанные конструктивные особенности счетчиков направлены на обеспечение условий ударной ионизации газов электронами при возможно более низком напряжении источника питания.
Инертные газы находятся в атомарном состоянии; при ионизации в качестве отрицательного иона они всегда имеют электроны (явления «прилипания» электронов к атомам этих газов не наблюдаются); электроны, обладай Массой, в несколько тысяч раз меньшей, чем у ионов, более подвижны, поэтому их легче разогнать до скоростей, при которых начинается ударная ионизация.

Рис. 11. Электрическое поле в газовом счетчике и расположении области ударной ионизации
Применение анода а виде тонкой нити с диаметром порядка десятых долей миллиметра позволяет значительно увеличить напряженность электрического поля около нее (рис. 11) по сравнению с полем между плоскими электродами при тех же условиях. Сила, действующая на электрон в электрическом поле и создающая ускоренное движение электрона к аноду, определяется напряженностью электрического поля (f=Eе). Однако кинетическая энергия и скорость движения (W =mv²/2) зависят не только от силы, но и от длины пути, пройденного электроном от одного соударения с атомом газовой среды до другого.
Уменьшение давления газа в счетчике увеличивает среднюю длину свободного пробега электронов в газе и, следовательно, также необходимо для получения условий ударной ионизации при более низком напряжении.
Ударная ионизация атомов газа электронами имеет место не во всем объеме счетчика, а только около нити (анода), где напряженность электрического поля достаточно большая. Пространство около анода счетчика, где возможна ударная ионизация, называют областью ударной ионизации (см. рис. 11).
Рассмотрим принцип работы газового счетчика.
При отсутствии ионизирующего излучения газ, наполняющий счетчик, содержит электрически нейтральные атомы, и свободных электрических зарядов, способных перемещаться под действием сил электрического поля, нет, поэтому электрического тока в цепи также нет. Предположим, что в рабочий объем счетчика проникла одна ионизирующая частица и создала там одну пару ионов. Под действием сил электрического поля положительный ион будет двигаться к катоду, а электрон — к аноду. В области ударной ионизации электрон, приобретающий достаточно большую скорость, ионизирует нейтральный атом при соударении с ним. В результате к аноду будут двигаться уже два электрона, которые, набрав скорость, будут также ионизировать атомы газа, вновь удваивая число электронов и ионов, и т. д.
Таким образом, вблизи анода газового счетчика происходит лавинообразное нарастание ионизации; в результате число электронов, падающих на анод, многократно увеличивается (от 10³ до 109 раз в зависимости от напряжения на счетчике). Длительность развития ионизации составляет миллионные доли секунды (микросекунды). За это время все электроны падают на поверхность анода, а тяжелые положительные ионы не успевают сколько-нибудь значительно переместиться с места своего образования, создавая вокруг анода слой («чехол») положительного пространственного заряда.
Постепенно положительные ионы относительно медленно перемещаются к катоду. Когда ион приближается к поверхности катода, он силой электрического поля своего заряда вырывает электрон катода и нейтрализуется.
Движение положительных ионов и электронов вызывает появление импульса тока в цепи счетчика и соответственно импульса падения напряжения на сопротивлении его нагрузки, что создает кратковременное уменьшение положительного напряжения на аноде. Таким образом, ионизирующая частица, создавшая хотя бы одну пару ионов в счетчике, фиксируется импульсом тока и напряжения, которые в свою очередь сравнительно просто можно зарегистрировать соответствующими регистрирующими устройствами, принцип работы которых будет рассмотрен ниже.
Форма импульсов напряжения на аноде счетчика приведена на рис.12
Характерной особенностью счетчиков является наличие так называемого мертвого времени, т. е. промежутка времени, в течение которого счетчик становится нечувствительным к радиоактивным частицам, создающим в его объеме новые первичные пары ионов.
Такое свойство счетчиков объясняется тем, что «чехол» положительных ионов, образующихся в области ударной ионизации, вместе с электронами, которые удерживаются на поверхности анода силами электрического притяжения к ионам, образует дополнительное электрическое поле. Благодаря этому напряженность результирующего электрического поля около анода уменьшается, настолько, что условия для ударной ионизации не обеспечиваются. Поэтому новые радиоактивные частицы не смогут создать новых импульсов газового разряда. В процессе движения ионов к катоду созданное ими дополнительное электрическое поле около анода уменьшается. Мертвое время в газовых счетчиках заканчивается тогда, когда напряженность поля около анода возрастет до величины, необходимой для ударной ионизации, и в первом приближении совпадет с длительностью импульса (см. рис. 12).
Рис.12 Форма импульсов напряжения на аноде счетчика
Мертвое время имеет величину порядка 10ˉ5—10ˉ3 сек. в зависимости от типа и режима работы счетчика.
Мертвое время ограничивает максимальную интенсивность излучений, которую способен регистрировать счетчик без существенных ошибок, т. е. определяет его разрешающую способность — максимальный счет радиоактивных частиц в единицу времени.
Вторая особенность счетчиков заключается в том, что ионы инертных газов, нейтрализуясь за счет вырванных из катода электронов, остаются в возбужденном состоянии и испускают избыточную энергию в виде фотонов ультрафиолетового излучения . Под воздействием этих фотонов из атомов катода могут быть выбиты новые электроны; последние ускоряются электрическим полем и могут дать начало развитию новому (на этот раз ложному) импульсу газового разряда в счетчике.
Таким образом, в газовом счетчике существуют условия для возникновения после воздействия одной радиоактивной частицы не одного, а целой серии следующих друг за другом импульсов. Такие счетчики, очевидно, непригодны для регистрации радиоактивных частиц, если не будут приняты специальные меры гашения газового разряда, исключающие появление ложных импульсов.
В зависимости от способа гашения разряда счетчики делятся на самогасящиеся и несамогасящиеся.
В несамогасящихся счетчиках с целью гашения газового разряда в анодную цепь включается высокоомное сопротивление нагрузки (порядка I08—109 ом). Импульс тока счетчика, вызванный движением ионов, создает на этом сопротивлении большое падение напряжения, поэтому напряжение на аноде счетчика значительно уменьшается и разряд прекращается. Вследствие большой величины сопротивления нагрузки напряжение на аноде счетчика восстанавливается очень медленно, отчего мертвое время счетчика значительно увеличивается. По этой причине счетчики такого типа называются медленными счетчиками; предельная скорость регистрации у них составляет не более 50—100 частиц в секунду.
Подобные счетчики на практике используются весьма редко.
Более широкое применение в настоящее время получили самогасящиеся счетчики. Для гашения разряда такие счетчики наполняются инертными газами с добавкой молекулярных газов, например паров спирта, метилаля и др. Молекулы гасящей примеси должны обладать работой (потенциалом) ионизации меньшей, чем работа ионизации атомов инертных газов. Ионы инертных атомов при движении к катоду сталкиваются с молекулами гасящей примеси и нейтрализуются за счет вырывания у них электронов. Таким образом, поверхности катода будут достигать только молекулярные ионы. Последние, вырывая электрон из катода, нейтрализуются и, оставшись в возбужденном состоянии, быстро распадаются (диссоциируются) на две более мелкие части (многоатомные молекулы распадаются на радикалы, т. е. группы атомов; двухатомные молекулы — на атомы). На разрушение молекулы затрачивается часть энергии; оставшаяся часть энергии возбуждения разбивается на две доли, каждая из которых мала и не может вызвать вылета электрона из поверхности катода.
Самогасящиеся счетчики с примесью многоатомного газа (например, метилалевые) имеют сравнительно высокое рабочее напряжение (порядка 800—1600 в) и ограниченный срок • работы, так как после каждого импульса уменьшается числю многоатомных молекул; через 10 — 108 импульсов оставшееся число многоатомных молекул становится недостаточным для нормальной работы счетчика.
Кроме того, счетчики с многоатомной гасящей примесью плохо работают при пониженной температуре (ниже —25° С).
В полевых дозиметрических приборах применяются исключительно галогенные самогасящиеся счетчики, в качестве гасящей примеси в которых применены молекулы брома и хлора. Теоретически срок службы таких счетчиков неограничен, так как атомы распавшихся молекул, соединяясь, вновь образуют молекулу.
Практически срок службы галогенных счетчиков ограничен, но он значительно больше, чем у спиртовых и метилалевых счетчиков.
К положительным свойствам галогенных счетчиков относятся их более низкое рабочее напряжение (360—400 в) и устойчивость работы в широком диапазоне температур (от -50° до +50° С).
Режимы работы газового счетчика зависят от величины приложенного напряжения. С целью выяснения особенностей различных режимов работы рассмотрим характеристику, приведенную на рис. 13, показывающую зависимость величины заряда, собираемого электродами за один импульс, от приложенного к счетчику постоянного напряжения. Кривая 1 соответствует импульсам с первоначальным числом пар ионов в три раза большим, чем у импульсов для кривой 2 (например, 300 пар ионов для кривой / и 100 пар ионов для кривой 2}.
При напряжениях, меньших U , счетчик работает в режиме импульсной ионизационной камеры; величина собранного электродами заряда в режиме насыщения равна суммарному заряду ионов, образованных радиоактивной частицей
∆q = n e.
При напряжениях больше U начинается ударная ионизация. Чем больше напряжение на счетчике, тем больше область ударной ионизации и тем большее число электронов будет падать на анод.
В диапазоне напряжений от U до U2 количество электронов (п ), падающих на анод, и их суммарный заряд (∆q ) пропорциональны первоначальному числу пар ионов

Рис.13 Зависимость величины электрического заряда, собираемого электродами за одна импульс, от напряжения на газовом счетчике; I — область ионизационной камеры; II— область пропорционального усиления; III — область ограниченной пропорциональности; IV — область самостоя тельного (гейгеровского) разряда; V — область непрерывного разряда (n ), образованных радиоактивной частицей. Газовые счетчики, работающие в этой области, получили название пропорциональных счетчиков. Если пренебречь утечкой заряда с электродов за время развития импульса тока в счетчике, то амплитуда импульсов напряжения на анодной нагрузке и на аноде счетчика будет

где ∆U - амплитуда импульса напряжения счетчика; Ссч - емкость счетчика (как конденсатора);
-коэффициент газового усиления, показывающий увеличение числа пар ионов за
- счет ударной ионизации.
Таким образом, в пропорциональных счетчиках амплитуда импульса напряжения U пропорциональна первоначальному числу пар ионов, образованных радиоактивной частицей, а коэффициент газового усиления является постоянной величиной. Однако величина коэффициента газового усиления в этом случае относительно небольшая (до 104== 10000 раз). Пропорциональные счетчики используются для регистрации сильно ионизирующих частиц, например альфа-частиц. Их преимущество заключается в том, что амплитуды импульсов от альфа-частиц во много раз больше амплитуды импульсов, создаваемых бета-частицами и гамма-квантами; благодаря этому регистрирующую схему можно отрегулировать так, что она будет считать только импульсы большой амплитуды, Что позволяет обнаруживать и измерять альфа-излучение при наличии бета- и гамма-излучений.
На участке напряжений от U2 до U3 счетчик работает в режиме ограниченной пропорциональности, т. е. с увеличением первоначального числа пар ионов амплитуда импульса увеличивается, но не пропорционально п0 (в большей степени увеличиваются импульсы с малым по); коэффициент газового усиления в этом режиме зависит от первоначального числа пар ионов — n0. Этот режим работы счетчиков практического применения не имеет.
При напряжениях от U3 до U счетчик работает в режиме самостоятельного газового разряда, при котором число образованных в области ударной ионизации пар ионов (n) и заряд, собираемый электродами (∆q=ne), не зависят от первоначального числа пар ионов (n ). Другими словами, амплитуда импульсов напряжения счетчика не зависит от того, создает ли ионизирующая частица всего одну пару ионов в объеме счетчика (например, вторичный электрон с малой энергией, возникший от гамма-кванта в стенке счетчика и проникший в его рабочий объем) или очень большое число пар ионов (например, 50 000 пар, созданных альфа-частицей); амплитуды импульсов напряжения счетчика будут одинаковыми. Характеристики 1 и 2 на рис. 13 для этой области сливаются в одну кривую. Счетчики, работающие в режиме самостоятельного газового разряда, принято называть счетчиками Гейгера-Мюллера. Они широко используются для регистрации бета-частиц и гамма-квантов и позволяют измерять малые активности и мощности доз гамма-излучения.
Если напряжение на счетчике превысит U , то гашение разряда вследствие очень большого числа образующихся при каждом импульсе ионов не обеспечивается и счетчик переходит в режим непрерывного газового разряда.
Конструктивные особенности газовых счетчиков в основном зависят от их назначения, т. е. от вида и энергии регистрируемых частиц и чувствительности счетчиков. Счетчики для регистрации альфа-частиц должны иметь окно, затянутое тонкой (обычно слюдяной) пленкой толщиной 1 — 2 микрона, сквозь которую альфа-частицы могут проникать в рабочий объем. Окно обычно размещено в торце стеклянного цилиндра, поэтому счетчики такой конструкции носят название торцовых счетчиков. К торцовым альфа -счетчикам относятся счетчики САТ-6 и САТ-7.

Рис. 14. Образцы газовых счетчиков: 1-СТС-5; 2 -АС-2; 3— МС-4; 4— МСТ-17; 5— САТ-7
Внешний вид некоторых газовых счетчиков приведен на рис. 14. Торцовые счетчики применяются также для регистрации бета-частиц с малой энергией (меньше 0,3 Мэв), однако толщина слюдяной пленки у них обычно больше, чем у торцовых счетчиков для регистрации альфа-частиц, и составляет 2 - 6 микрон. К такому виду счетчиков относится счетчик МСТ-17.
Для регистрации бета-частиц сравнительно большой энергии (больше 0,3 — 0,5 Мэв) обычно применяются цилиндрические счетчики с тонким (10 — 30 микрон) алюминиевым (для спиртовых и метилалевых счетчиков) или стальным (для галогенных счетчиков) корпусом-катодом. К таким счетчикам относятся счетчики АС-2 (алюминиевый самогасящийся 2-й образец), СТС-5 и СТС-6 (стальной самогасящийся) .
Для регистрации гамма-излучения применяются счетчики с толстыми стенками (с толстым катодом из меди или других материалов).
Обычные цилиндрические бета-счетчики также широко используются для регистрации гамма-излучений; при этом они помещаются в достаточно толстый алюминиевый чехол, поглощающий бета-излучения.
Одной из важнейших характеристик, определяющих свойства счетчика как датчика дозиметрических приборов, является его эффективность. Эффективностью называется отношение числа радиоактивных частиц, вызвавших импульс газового разряда, к общему числу частиц, попавших в рабочий объем счетчика. Эффективность газовых счетчиков к альфа- и бета-частицам близка к 100%.
Однако указанную эффективность к бета-частицам не следует путать с эффективностью регистрации потока бета-частиц, воздействующих на внешнюю поверхность счетчика; последняя может иметь величину от близкой к 100% до нуля в зависимости от энергии бета-частиц и толщины стенок счетчика.
Эффективность счетчиков к гамма-квантам значительно меньше и имеет величину от 0,2 до 1,6%. Гамма-кванты регистрируются счетчиком главным образом за счет вторичных электронов, выбиваемых гамма-квантами из материала стенок счетчика. Поэтому эффективность зависит от энергии квантов, материала стенок и до некоторой степени от их толщины.
Так, у счетчиков, прикрытых достаточно толстым слоем алюминия (порядка 5 — 8 мм), в диапазоне энергий гамма-квантов от 0,2 до 2,5 Мэв эффективность изменяется в пределах от 0,1 до 1,2%, возрастая примерно пропорционально энергии. Благодаря этому скорость счета импульсов счетчика N, т. е. число импульсов в единицу времени, характеризует мощность дозы гамма-излучения в указанном диапазоне энергий квантов. Действительно,
где Sсч — рабочая поверхность счетчика, на которую воздействует гамма -излучение;
εγ — эффективность счетчика;
. Пγ— плотность потока гамма-квантов, зависящая от мощности дозы и энергии квантов:
Коэффициент поглощения µа гамма-излучения в воздухе в диапазоне энергий квантов от 0,1 до 2 Мэв практически является постоянной величиной поэтому:



где - практически постоянная величина, зависящая от величины рабочей поверхности счетчика.
Таким образом, чувствительность счетчика при измерении мощностей доз гамма-излучения зависит от величины поверхности его рабочего объема. Чем больше поверхность, тем большее число гамма-квантов будет воздействовать на нее в единицу времени при данной мощности дозы, тем чувствительнее счетчик. Однако с увеличением чувствительности уменьшается верхний измеряемый предел мощностей доз, так как предельная скорость счета ограничивается «мертвым временем» счетчика.
Так, например, предельная измеряемая мощность дозы гамма-излучения для счетчика СТС-5 составляет около 0,5 р/час. Путем уменьшения габаритов и рабочего объема созданы счетчики, обеспечивающие измерение мощностей доз до 5 р/час, до 50 р/час и больше.
Счетчики такого типа получили название малочувствительных.
Оценка качества счетчика и определение его рабочего напряжения обычно производятся по его счетной характеристике. Для снятия такой характеристики газоразрядный счетчик подключается к пересчетной установке, т. е. такой регистрирующей схеме, которая позволяет считать число возникающих на нагрузке счетчика импульсов напряжения, амплитуда которых превосходит некоторую пороговую величину. Счетной характеристикой называется зависимость зарегистрированного числа импульсов в единицу времени от напряжения питания счетчика при постоянной интенсивности облучения.
Счетная характеристика имеет вид, представленный на рис. 15. Как видно из рисунка, при напряжении на счетчике меньше U импульсы не регистрируются пересчетной установкой, так как они очень малы. Напряжение Uн, при котором появляется счет импульсов, называется напряжением начала счета. При дальнейшем увеличении напряжения скорость счета быстро увеличивается. В этой области счетная установка регистрирует не все попадающие в счетчик частицы, так как импульсы напряжения счетчика имеют разную величину в зависимости от первичной ионизации и других причин. Начиная с точки A и до точки Б, скорость счета почти не изменяется с возрастанием напряжения, т. е. на участке А — Б практически все частицы, производящие в счетчике начальную ионизацию, регистрируются.
 |
Рис. 15 Счетная характеристика газового счетчикаЭтот почти горизонтальный участок характеристики носит название «плато». Некоторое наблюдаемое увеличение скорости счета на участке «плато» объясняется появлением и увеличением числа ложных импульсов вследствие того, что гасящие примеси самогасящегося счетчика не обеспечивают гашение всех без исключения ложных импульсов.
При напряжениях больше UБ наблюдается резкий рост ложных импульсов и переход к непрерывному разряду. Рабочим участком счетной характеристики является «плато». Чем больше протяженность и меньше наклон «плато», тем лучше качество счетчика. Наклон «плато» принято оценивать увеличением скорости счета импульсов при изменении напряжения на 100 в, выраженным в процентах к средней скорости счета на участке «плато»:
У хороших счетчиков протяженность (ширина) «плато» порядка 100—200 в и наклон не превышают нескольких процентов. В самогасящихся счетчиках по мере распада многоатомных молекул гасящей примеси счетная характеристика постепенно ухудшается — укорачивается протяженность «плато» и увеличивается его наклон. Последнее вызывает необходимость проверки счетчиков в процессе работы с ними, так как могут появиться значительные ошибки в измерениях. Галогенные счетчики обладают значительно более устойчивой счетной характеристикой.
Рабочее напряжение счетчика выбирают в пределах «плато», учитывая, что излишне большое напряжение увеличивает амплитуду импульсов и счетчик будет быстрее выходить из строя; слишком малое напряжение (около начала «плато») вызывает опасность значительного уменьшения скорости счета импульсов вследствие случайного уменьшения напряжения питания.
В лабораторных приборах напряжение счетчика выбирается около середины счетной характеристики (50—80 в от напряжения начала счета).
Одним из параметров счетчика является его фон. Фон счетчика — это средняя скорость счета импульсов при рабочем напряжении и в отсутствии радиоактивных источников. Он определяется всеми посторонними ионизирующими излучениями: природным радиоактивным излучением земли и всех окружающих предметов, космическими излучениями и т. д.
Даже световое излучение (особенно прямые лучи солнца) способно вызывать появление импульсов в газоразрядном счетчике, если его рабочий объем не защищен светонепроницаемым слоем вещества.
Если счетчик помешен в свинцовое защитное устройство (свинцовый домик) с толщиной стенок 50 мм, то фон почти полностью обуславливается космическими лучами и природными загрязнениями радиоактивными веществами материалов, из которых сделаны счетчик и защитное устройство. Фон счетчика, замеренный в указанных условиях, называется темновым фоном и приводится в его паспортных данных.
V. СЧЁТЧИК ГЕЙГЕРА С ВЫСОКОВОЛЬТНЫМ ПИТАНИЕМ ОТ ПРЕОБРАЗОВАТЕЛЯ ПОСТОЯННОГО НАПРЯЖЕНИЯ НА ПОЛУПРОВОДНИКОВОМ ТРИОДЕ
Для разработки схемы счётчика слабого бета-излучения используем схему, приведённую на рис.16.
В схеме счётчика Гейгера, изображённой на рис.16, для питания лампы используется преобразователь напряжения на полупроводниковых приборах. Преобразователь состоит из генератора по трёхточечной схеме на полупроводниковом триоде 2N107, повышающего трансформатора и селенового выпрямителя с фильтром. Преобразователь преобразует напряжение 6-вольтовой батареи Б в стабилизированное напряжение 300 в постоянного тока, необходимое для питания лампы 1В86.
Индуктивностью колебательного контура генератора служит первичная обмотка малогабаритного трансформатора Тр1. Для осуществления обратной связи от неё сделан отвод. Возникающие колебания возбуждают во вторичной обмотке высокое напряжение, которое выпрямляется высоковольтным селеновым выпрямителем. Пульсации сглаживаются конденсатором С2. четыре последовательно соединённые неоновые лампы NE-2 и сопротивление R1 образуют стабилизатор напряжения.
Импульсы с лампы 1В86 счётчика через трансформатор Тр2 подаются на индикатор.
В штепсельные гнёзда “Тел.” могут быть включены телефоны для слуховой индикации. Германиевый диод 1N34 выпрямляет импульсы, и получающийся постоянный ток отклоняет стрелку микроамперметра постоянного тока М (для визуальной индикации). Величину тока в цепи микроамперметра можно регулировать реостатом R3.
Схему, приведённую на рис.16 немного упростим, но так, чтобы можно было использовать в ней в качестве счётчика- счётчик Гейгера. (см.рис.17)

Рис.17 счётчик слабого бетта-излучения
VI. Счётчик СТС-5
Выписка из паспорта счётчика СТС-5, который мы будем использовать в качестве проверки работоспособности нашей схемы с рис.17. На рис.14 изображён внешний вид счётчика СТС-5. Его длина 110±25 мм, анодный выход обозначен знаком “+”.
а) Основные типовые параметры:
1. Напряжение начала отсчёта……………………………….280 ÷ 330 В
2. Рекомендуемое рабочее напряжение……………...............360 ÷ 440 В
3. Наименьшая протяжённость плато...……………………………...80 В
4. Наибольший наклон плато……………………………...0,125% на 1В
5.Наибольший натуральный фон……………………………27 имп. в мин
б) Условия эксплуатации
1.Сопротивление нагрузки………………………………от 5 до 10 Мом.
2. Наибольшая нагрузочная ёмкость, доступная во входной цепи счётно-измерительного устройства………………………………………...10 пф.
3. Переходная ёмкость входа счётного прибора……………….7 ÷ 15 пф
4. Допустимые колебания температуры окружающей среды…от-40˚С до +50˚С
5.Для обеспечения продолжительной и устойчивой работы счётчика следует:
а) не допускать попадания на счётчик всякого рода загрязнений, могущих ухудшить его изоляционные свойства;
б) оберегать счётчик от ударов и механических повреждений;
в) при включении счётчика соблюдать соответствующую полярность – положительный полюс источника питания присоединять к анодному выводу счётчика, обозначенному знаком “+”, а отрицательный полюс источника питания присоединять к катодному выходу счётчика, не имеющему обозначения.
VII. СХЕМА УДВОЕНИЯ НАПРЯЖЕНИЯ
Исходя из паспортных данных [см. VI а) -2] в схеме (рис.17) используется схема удвоения напряжения.
Принципиальная схема и осциллограммы напряжения в различных точках выпрямителя приведены на рисунке.
U2 - Напряжение вторичной обмотки трансформатораUн – Напряжение на нагрузке.
Отличительной особенностью данной схемы является то, что в одном полупериоде переменного напряжения от вторичной обмотки трансформатора “заряжается” один конденсатор, а во втором полупериоде от той же обмотки– другой. Поскольку конденсаторы включены последовательно, то результирующее напряжение на обоих конденсаторах ( на нагрузке) в два раза выше, чем можно получить от той же вторичной обмотки в схеме с однополупериодным выпрямителем.
Преимущества: Вторичную обмотку трансформатора можно расчитывать на значительно меньшее напряжение.
Недостатки: Значительные токи через вентили выпрямителя, Уровень пульсаций значительно выше, чем в схемах двухполупериодных выпрямителей.
Эта же схема может использоваться еще в двух вариантах:
Левая схема предназначена для получения двух напряжений питания одной полярности, правая – для получения двуполярного напряжения с общей точкой.
Во втором варианте схемы характеристики выпрямителя соответствуют характеристикам однополупериодного выпрямителя.
VIII. СЧЁТЧИК “СЛАБОГО БЕТА-ИЗЛУЧЕНИЯ”. СТБ-13
В схеме рис.17 заменим счётчик СТС-5 на счётчик СТБ-13. С его помощью у нас есть возможность регистрировать слабее бета-излучение.
Счётчик СБТ-13 (паспортные данные)
Счётчик бета-излучения СБТ-13 предназначен для регистрации мягкого бета-излучения в полевых и лабораторных условиях.
Схема соединения электродов с выводами:

А-анод
К-катод
Основные электрические параметры:
Рабочее напряжение, В 380
Напряжение начала отсчёта, В 250-300
Протяжённость плато счётной характеристики, В, не менее 70
Наклон плато счётной характеристики,  , не более 0,15 , не более 0,15
Чувствительность, 100-140 100-140
Собственный фон, 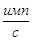 , не более 0,6 , не более 0,6
Амплитуда импульса напряжения, В, не менее 20
Эффективность регистрации бета-излучения,%, не менее 45
Допустимый режим эксплуатации:
| Наименование параметра |
Норма |
| Рабочий интервал напряжения, В |
320 – 450 |
Наибольшая рабочая мощность эксплуатационной дозы гамма излучения, А/кг ( ) ) |
5,16 · 10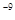 (20) (20) |
| Наибольшая рабочая скорость счёта, имп/с |
1900 - 3000 |
Указания по эксплуатации:
При эксплуатации счётчика значения величин, определяющих режим эксплуатации, не должны выходить за указанные значения.
Для продолжительной и устойчивой работы счётчика необходимо:
А) не допускать попадания на счётчик всякого рода загрязнений, могущего ухудшить его изоляционные свойства;
Б) оберегать счётчик от ударов и механических повреждений;
В) при включении счётчика соблюдать полярность.
3. Остальные условия по эксплуатации ССЗ 394 022 ТУ
Драгоценных металлов не содержит.
IX. РАЗРАБОТКА МИКРОСХЕМЫ ДЛЯ СЧЁТЧИКА СЛАБОГО БЕТА-ИЗЛУЧЕНИЯ
После тщательной проверки работоспособность схемы (рис.17) с счётчиком СТБ-13, необходимо разработать микросхему, чтобы наш счётчик был компактным и удобным в применении.

А – счётчик СТВ-13 (4-ый контакт);
Б – счётчик СТВ-13 (8-ой контакт);
В – трансформатор (5-ый вывод);
Г – индикатор;
Д – миллиамперметр;
Е – трансформатор (8 – ой вывод);
Ж – трансформатор (6 - ой вывод);
З – миллиамперметр.
X. ПРИМЕНЕНИЕ СЧЁТЧИКА
С помощью счётчика слабого бета – излучения можно зафиксировать рентгеновские лучи.
При наблюдении дифракции рентгеновских лучей, отражающие плоскости могут быть расположены либо параллельно поверхности образца, либо перпендикулярно.
В первом случае говорят, что кристалл вырезан по геометрии Брега.
Во втором случае говорят, что кристалл вырезан по геометрии Лауэ. (рисунок 18)
Рассмотрим аномальное прохождение рентгеновских лучей .Направим параллельный пучок монохроматических рентгеновских лучей параллельно плоскости. Если на пути этого луча ,проходящего сквозь пластинку, поставить счетчик слабого бета излучения ,то можно будет зафиксировать рентгеновское излучение.(рисунок 19)
Обозначим интенсивность падающего луча J0 ,а выходящего J,тогда получим зависимость:
J=J0 ·exp(-μ0 · t)
μ0 - линейный (фотоэлектрический) коэффициент поглощения фотоэлектрических лучей .Зависит от сорта атомов исследуемого образца.
Если пластина вырезана из монокристалла ,удовлетворяющего модели идеального кристалла, то поворачивая кристалл относительно нормали к поверхности образца и плоскости рисунка до тех пор пока угол скольжения Q не станет равным углу Q из условия Вульфа-Брега :
2·d· sin Q =λ (рисунок 19 лучи 2, 2’ и 2”)
Регистрируя счетчиком прямой и отраженные лучи мы можем прийти к соотношению :
J =J =J = 0,25 ·J0 ·exp(- μ = 0,25 ·J0 ·exp(- μ · t) · t)
μ - интерференционный коэффициент поглощения (аномальный).Получаем ,что здесь интенсивность больше ,чем в случае параллельного прохождения рентгеновских лучей ,так как μ - интерференционный коэффициент поглощения (аномальный).Получаем ,что здесь интенсивность больше ,чем в случае параллельного прохождения рентгеновских лучей ,так как μ > μ0 (для Ge , Si , GaAs ) > μ0 (для Ge , Si , GaAs )
Впервые это явление обнаружил немецкий физик Борман. Для наблюдения эффекта Бормана кристалл должен удовлетворять условиям :
Кристалл должен быть практически бездефектным, идеальным.
Кристалл должен быть “толстым”, удовлетворять условию: μ0 · t  10 10
Аномальное прохождение будет возможно лишь при условии выполнения условия Вульфа – Брега.
СПИСОК ЛИТЕРАТУРЫ
1. “Дозиметрические приборы”, под редакцией Г.А. Абрамова, Москва, 1958г.
2. “Схемы с полупроводниковыми приборами” (сборник переводов) под редакцией Малинина Р.М., Военное издательство: Москва, 1960г.
|