Московский Авиационный Институт
(МАИ)
Отчет
По лабораторной работе №1
Тема:
"Исследование устойчивости, решение задач линейного программирования графическим способом"
Отчет выполнила:
Студентка М-22 группы
Косьяненко А.Е.
Серпухов, 2010г.
Цель работы
Применить теоретические сведения на практике, исследовать устойчивость, а также научиться решать задачи линейного программирования графическим способом.
Задание:
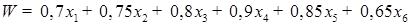
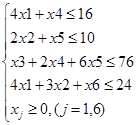
Решение
Заданная система уравнений-ограничений состоит из четырех уравнений-ограничений 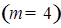 и имеет шесть переменных и имеет шесть переменных 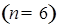 , поэтому данную задачу можно решить графическим способом , поэтому данную задачу можно решить графическим способом 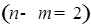 на плоскости. Для этого необходимо выразить все неизвестные через две независимые переменные, в качестве которых, например, можно принять на плоскости. Для этого необходимо выразить все неизвестные через две независимые переменные, в качестве которых, например, можно принять 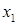 и и 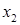 , являющиеся в таком случае координатными осями графика. , являющиеся в таком случае координатными осями графика.
Из системы уравнений-ограничений следует:
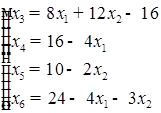
Подставляя полученные значения получим уравнение целевой функции:
W=0.7х1+0.75х2+60.8+-1.6(16-2х1)-4.8(10-2х2)+14.4-3.6х1+8.5-1.7х2+15.6-2.6х1-1.95х2=0.9х1+6.7х2+25.7
Каждому из этих неравенств соответствует полуплоскость на графике, образующих ОДР, выделенную точками  . .
Точки(х2=0, х1=2; х2=1, х1=0.5; х1=4; х2=5; х2=0, х1=12; х2=4, х1=6)
Опираясь на уравнение ЦФ необходимо определить точку в ОДР, а значит и значение 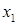 и и 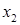 , максимизирующую ЦФ. , максимизирующую ЦФ.
Можно по существующей зависимости между 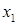 и и 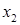 (при (при 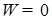 ) построить основную линию (проходящую из начала координат), используя следующее уравнение: ) построить основную линию (проходящую из начала координат), используя следующее уравнение:
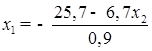 .(1.12) .(1.12)
Далее можно построить вектор-градиент 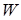 , который будет исходить из начала координат , который будет исходить из начала координат 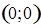 в точку в точку 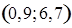 , т.к. вектор-градиент можно найти следующим образом: , т.к. вектор-градиент можно найти следующим образом:

Найдем максимальные и минимальные значения функции: Max(5;2); min(0;2).
Подставим значения в целевую функцию:
W=1.4+3.45+48+7.2+0.65=61
Ответ:61.
Если изменить значение в заданной линейной задаче, то можно высчитать результат:
W=0.7х1+0.85х2+0.8х3+0.9х4+0.85х5+0.65х6
Упростим до целевой функции:
W=0.9х1+6.8х2+25.7
Х1=2
Х2=5
Х4=8
Х5=0
Х6=1
х3=60
Рассчитываем значение целевой функции:
W=0.7*2+0.85*5+0.8*60+0.9*8+0.65=61,5
Вывод
В ходе лабораторного занятия, я освоила теоретические знания на практике, познакомилась с графическим способом решения задач линейного программирования.
|