Контрольная работа: Классический метод расчета переходных процессов в линейных цепях

Название: Классический метод расчета переходных процессов в линейных цепях
Раздел: Рефераты по физике
Тип: контрольная работа

Содержание

1. Возникновение переходных процессов и законы коммутации

2. Способы получение характеристического уравнения

3. Особенности переходных процессов в цепях с одним реактивным элементом

4. Переходные процессы в цепях с двумя разнородными реактивными элементами

5. Временные характеристики цепей

6. Расчет реакции линейной цепи на входное воздействие произвольного вида с применением временных характеристик цепи

Список используемых источников

1. Возникновение переходных процессов и законы коммутации

Для изучения темы реферата необходимо знать расчет установившихся режимов, т.е. таких, когда все токи и напряжения либо постоянные, либо периодически повторяющиеся функции времени, но в любой схеме могут происходить подключения и отключения ветвей (происходит коммутация). Обозначают коммутацию: . В линейных цепях коммутация считается идеальной, т.е.:

1) ключ представляет собой либо разрыв, либо провод;

2) длительность перехода из одного состояния в другое равна нулю. Момент времени сразу после коммутации обозначают либо , а момент времени непосредственно перед коммутацией соответственно обозначают , . После коммутации цепь стремится под действием источников схемы прийти к новому установившемуся режиму, но для этого ей требуется время. Процессы, происходящие в цепи после коммутации, называются переходными процессами.

Почему этот переход не может произойти мгновенно? Дело в том, что в цепи имеются элементы L и C, в которых запасается определенная величина энергии W_L =L² /2 и W_C =Cu² /2 соответственно. В новом установившемся режиме будет другой запас энергии, и, т.к. скорость изменения энергии есть подводимая к элементу мощность, получается, что требуется конечное время на изменение этого запаса энергии (т.к. источников бесконечной мощности в реальной цепи нет). Из выражения для W_L и W_C и того факта, что в цепях не развивается бесконечная мощность, вытекают два фундаментальных условия, без которых невозможно рассчитать ни один переходной процесс – это законы коммутации.

Получим их:

т.к. P, L - конечное число, _L - конечное число, то - скачка быть не может. Отсюда вытекает один из законов коммутации: ток в индуктивности не может измениться скачком, поэтому при коммутации: . Дифференцируя dW_C /dt, приходим ко 2-ому закону коммутации: напряжение на ёмкости не может измениться скачком, поэтому при коммутации: . Т.к. = L_L , , то можно использовать и такие функции: , .

Про остальные величины, в том числе и про скорость изменения любых токов и напряжений при коммутации заранее ничего не известно и их приходится рассчитывать. Т.к. и форма изменения токов и напряжений неизвестна, приходится использовать самые общие выражения: , . Тогда уравнения, описывающие цепь после коммутации, оказываются дифференциальными. В линейной цепи – это линейные дифференциальные уравнения (ЛДУ). Существуют различные методы решения таких уравнений, и соответственно различают различные методы расчета переходных процессов.

2 Способы получение характеристического уравнения

Классический метод

Классический метод основан на решении ЛДУ методом вариации произвольных постоянных. Любая система ЛДУ может быть сведена к одному уравнению n –ого порядка. В цепях по схеме после коммутации порядок определяется так: n = n_L + n_C – n_ОК – n_ОС , где n_L – число L; n_C – число C; n_ОК – число особых контуров, т.е. таких, которые состоят только из емкостей и источников ЭДС; n_ОС – число особых сечений (в простейшем случае, это узлы схемы, к которым подключены только ветви с источником тока или с индуктивностями).

Решение уравнения представляют в виде суммы частного решения неоднородного уравнения (ЛНДУ) и общего решения линейного однородного дифференциального уравнения (ЛОДУ). Частное решение определяется видом правой части уравнения. В цепях в правой части уравнения стоят источники энергии схемы после коммутации. Физический смысл частного решения уравнения в цепях – это новый установившийся режим, к которому будет стремиться схема после коммутации под действием источников. Поэтому частное решение ЛНДУ называют принужденной составляющей режима. Общее решение ЛОДУ физического смысла не имеет. В противоположность принужденной составляющей, его называют свободной составляющей переходного процесса. Свободная составляющая записывается в виде суммы слагаемых, число и вид которых определяются корнями характеристического уравнения.

После записи решения необходимо рассчитать произвольные постоянные, вошедшие в выражение общего решения. Это можно сделать, если известны начальные условия. Начальные условия – это значения искомой функции времени и необходимого числа её производных по времени в начале переходного процесса, т.е. при t=0.

Все начальные условия делят на две группы:

- независимые начальные условия, это _L (0) и u_C (0), которые находятся по законам коммутации, с помощью вычисленных ранее _L (0_- ) и u_C (0_- ) в схеме до коммутации;

- все остальные начальные условия – зависимые. Их приходится искать из цепи после коммутации в переходном режиме по законам Кирхгофа для мгновенных значений токов и напряжений при t=0 с помощью независимых начальных условий. Имея необходимое число начальных условий и рассматривая решение и его производные по времени в момент , получают систему линейных алгебраических уравнений (СЛАУ) из которой находят произвольные постоянные.

В соответствии с изложенным, порядок расчета переходного процесса классическим методом может быть таким:

1) рассматривают установившийся режим схемы до коммутации и находят _L (0_- ) и u_C (0_- );

2) рассматривают цепь после коммутации в новом установившемся режиме и находят принужденную составляющую переходного процесса;

3) тем или иным способом получают характеристическое уравнение и находят его корни в соответствии с которыми определяют вид свободной составляющей;

4) записывают решение в виде суммы принужденной и свободной составляющих.Если характеристическое уравнение n – ого порядка, то формируется система линейных алгебраических уравнений (СЛАУ) n - ого порядка, включающая (n-1) производную решения. Переписывают СЛАУ для ;

5) рассматривают цепь после коммутации в переходном режиме; рассчитывают необходимые начальные условия (ННУ);

6) подставляют ННУ в СЛАУ при и находят произвольные постоянные;

7) записывают полученное решение.

Способы получения характеристического уравнения

Существуют различные способы получения характеристического уравнения.

Если цепь описывается всего одним уравнением, то его алгебраизируют: d/dt заменяют на p, dt заменяют на 1/p, правую часть обращают в ноль и получают характеристическое уравнение.

Если режим в цепи описывается системой из нескольких уравнений, то методом подстановки их сводят к одному и поступают точно также как описано выше (обычно так не делает).

Универсальный способ

Систему уравнений по законам Кирхгофа для цепи после коммутации алгебраизируют и составляют определитель системы, и приравняв его к нулю, получают характеристическое уравнение.

Воспользуемся этим способом.

Пусть схема после коммутации имеет вид:

, ,

Если в схеме нет управляемых источников и взаимных индуктивностей, то проще всего поступить так: в схеме после коммутации все источники заменить их внутренним сопротивлением, вместо индуктивности L написать pL, вместо емкости C написать .

а) Если в полученной схеме нет ветви без сопротивления, томожно разомкнуть любую ветвь полученной пассивной схемы и относительно точек разрыва записать выражение для нахождения .

б) Если в полученной схеме есть ветви без сопротивления, то размыкать надо именно ту ветвь, в которой ищется переходный ток или напряжение и относительно точек разрыва записывают .

Характеристическое уравнение имеет вид:

Для рассмотренного выше примера получим:

Выражение для свободной составляющей содержит столько слагаемых, сколько есть корней, а слагаемые имеют такой вид:

а) каждому простому вещественному корню соответствует слагаемое .

Если два корня, то процесс апериодический.

б) двум комплексно-сопряженным корням: и соответствует A₁ e^Px ¹ ^t +A₂ e^Px ² ^t , где A₁ , A₂ – получаются комплексными числами, причем комплексно-сопряженными числами. Поэтому с помощью формулы Эйлера этот результат можно записать в другом виде (где не будет j): .

По этому выражению не очень удобно строить графики. Используя формулы тригонометрии его можно преобразовать (либо в sin, либо в cos): Ce^- ^t sin(_c t+₁ )=De^- ^t cos(_c t+₂ ) – затухающий во времени гармонический процесс – колебательный процесс.

в) среди корней есть m одинаковы[ (если таких корней два, то переходный процесс называется критическим).

;

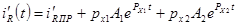
Пример: Дано: E=40В, R1=R2=400 Ом, L=5Гн, C=5 мкФ. Найти .

1) В схеме до коммутации стоит постоянный источник, следовательно, ток в установившемся режиме постоянный.

t<0

, .

Если источник ЭДС синусоидальный, то эту часть задачи решают символическим методом.

2) Рассчитывают новый установившийся режим, находят принужденную составляющую.

Видно, что после коммутации в схеме есть только постоянный источник ЭДС и поэтому в принужденном режиме – постоянный ток.

3) получают характеристическое уравнение

4) записывают решение

5) определяют начальные условия

Для схемы после коммутации записывают систему уравнений по законам Кирхгофа. Число этих уравнений больше, чем число неизвестных, однако при t=0, известны все i_L (0) и u_C (0), поэтому при добавлении этих независимых условий из полученной при t=0 системы можно найти все остальные зависимые начальные условия, например, методом подстановки.

При решении надо выразить значения токов и напряжений в момент t=0, их производные по времени в момент t=0 через параметры элементов схемы и независимые начальные условия.

Например, для нашей задачи:

В нашей задаче для расчета надо найти 2 начальных условия, т.к. имеем 2 корня характеристического уравнения и 2 произвольные постоянные, поэтому надо знать _R (0) и _R (0).

Из (1):

Из (3):

6) расчет произвольных постоянных

В нашем случае:

При :

Тогда из (1)

Из (3)(2)

Ответ: , А.

3. Особенности переходных процессов в цепях с одним реактивным элементом

В таких цепях характеристическое уравнение будет первого порядка. Получить это уравнение можно, например, так:

По способу Zвх(p)=0, при этом схемы могут иметь вид:

Рис (1) , ,

Рис (2) , .

Видно, что корень характеристического уравнения получается отрицательным, т.е. с течением времени свободная составляющая .

Ясно, что в разных схемах различными получаются величина А, величина , но свободная составляющая всегда будет иметь вид затухающей экспоненты. Для таких функций вводятся специальная характеристика.

Постоянная времени цепи (τ) – есть интервал времени, за который амплитуда свободной составляющей уменьшается в e раз.

Воспользовавшись этим определением, можно найти τ таким образом так как , то

В цепи: ,

т.е. τ зависит только от параметров рассматриваемой цепи (τ не зависит от начальных условий и напряжений источника).

Используя понятие τ, можно условно ввести понятие длительности переходного процесса. Так как , то

t	τ	3τ	5τ
	0,36	0,05	0,004

В соответствие с этой таблицей принимают, что переходный процесс длится . К концу этого времени график переходного процесса практически сливается с принужденной составляющей.

Если известен график переходного процесса, из него можно найти τ.

Проще всего сделать так: на глаз определить, где кончается переходный процесс.

Длительность переходного процесса делят на . Это и будет τ.

- Из графика переходного процесса вычитают принужденную составляющую. Это будет график свободной составляющей. Задаются моментом времени t₁ и находят из графика x_св (t₁ ). Делят эту величину на e и получают x_св (t₁ + τ). Находят на графике эту величину, из нее определяют время t₂ и затем находят τ как τ = t₂ - t₁

- τ есть величина под касательной к графику переходного процесса. Подкасательная – это проекция на ось времени от точки, в которой проведена касательная до точки пересечения этой касательной с асимптотой.

Пример: Дано: , , . Найти i(t), u_c (t)

1) t<0

i(0_)=0, u_c (0_)=0,

2) t→∞

, ,

Должен существовать переходной процесс, в течении которого от источника энергия передается к конденсатору, а по проводам идет ток, заряжающий конденсатор.

3),

4) ; ,

, ,

5) Расчет начальных условий.

Тогда из получают

Пример: Дано: , , . Найти .

, ,

2) Расчет принужденной составляющей.

В данном случае принужденный режим есть синусоидальный ток, поэтому расчет проведем символическим методом.

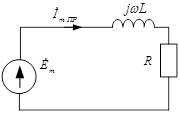
Переходят к мгновенному значению:

3) ; ,

6) ,

График проще всего построить по этапам:

1) принужденная составляющая;

2) exp соответствует свободной составляющей суммы этих графиков.

4. Переходные процессы в цепях с двумя разнородными реактивными элементами

В этих цепях характеристическое уравнение имеет второй порядок, следовательно, будет два корня и две произвольные постоянные в свободной составляющей. Самое главное это то, что у квадратного уравнения есть 3 типа корней (вещественные различные, вещественные одинаковые и пара комплексно-сопряжённых), поэтому вид свободных составляющих в разных цепях получается различным. Рассмотрим возможные варианты на простейших примерах.

Пример:

1) i_L (0_) = 0, u_c (0_)=0,

2) i_пр = 0, u_R _пр = i_пр R = 0

u_C _пр = E, u_L _пр = 0

3) Будем искать ток в цепи. Тогда надо иметь два начальных условия: i(0) и i΄(0).

Для цепи после коммутации:

В данной схеме все 3 способа получения характеристического уравнения имеют одинаковую трудоёмкость.

, ,

В зависимости от величины подкоренного выражения получаются разные типы корней.

Если , то подкоренное выражение равно нулю, и следовательно получим . Из выражения (*) видно, что это получается при некотором «критическом» значении сопротивления .

Если же R > R_кр то подкоренное выражение положительно, и получим два вещественных различных корня. Если R < R_кр , под корнем будет отрицательное число, и получим пару комплексно сопряжённых корней.

1) R > R_кр (два вещественных различных корня) и тогда решение для тока запишется в виде:

и при t = 0 получаем два уравнения для расчёта произвольных постоянных:

Из (1): , и подставляя в (2):

График проще построить по частям (принуждённая составляющая и каждое слагаемое свободной составляющей, а затем сложить).

Говорят, что это апериодический процесс.

Аналогично можно получить выражения и графики для напряжения на электродах:

2) R = R_кр

при

Графики имеют в этом случае точно такой же вид, как и в предыдущем случае, но в первом случае процессы идут медленнее, чем во втором. Этот случай называется критическим переходным процессом.

3) R < R_кр

, ,

т.е. при α→ 0 ω_c стремится к резонансной частоте данной цепи.

Решение запишется в виде:

(классический метод)

(1) в (2):

(1)/(3): , из (3)

Видно, что в данном случае свободная составляющая представляет собой затухающую во времени синусоиду. Такой переходной процесс называется колебательным или периодическим, и график его проще построить так: симметрично относительно принуждённой составляющей строим график амплитуды свободной составляющей (график огибающей процесса), дальше в график огибающей вписывают синусоиду с её начальной фазой и периодом свободных колебаний.

, - коэффициент затухания,

- частота свободных колебаний.

Рассматривать цепи более высокого порядка смысла нет, потому что у любого уравнения корни могут быть трёх видов, а для каждого типа корней мы свободную составляющую уже получили.

5. Временные характеристики цепей

Ранее мы рассматривали частотные характеристики, а временные характеристики описывают поведение цепи во времени при заданном входном воздействии. Таких характеристик всего две: переходная и импульсная.

Переходная характеристика

Переходная характеристика - h(t) - есть отношение реакции цепи на входное ступенчатое воздействие к величине этого воздействия при условии, что до него в цепи не было ни токов, ни напряжений.

Ступенчатое воздействие имеет график:

1(t) – единичное ступенчатое воздействие.

Иногда используют ступенчатую функцию, начинающуюся не в момент «0»:

Для расчёта переходной характеристики к заданной цепи подключают постоянный ЭДС (если входное воздействие – напряжение) или постоянный источник тока (если входное воздействие – ток) и рассчитывают заданный в качестве реакции переходный ток или напряжение. После этого делят полученный результат на величину источника.

Пример: найти h(t) для u_c при входном воздействии в виде напряжения.

1) ,

2) ,

3) , ,

Пример : ту же задачу решить при входном воздействии в виде тока

1) ,

2) ,

3) , ,

Импульсная характеристика

Импульсная характеристика - g(t) – есть отношение реакции цепи на входное воздействие в виде дельта - функции к площади этого воздействия при условии, что до подключения воздействия в схеме не было ни токов, ни напряжений.

δ(t) – дельта-функция, дельта-импульс, единичный импульс, импульс Дирака, функция Дирака. Это есть функция:

Рассчитывать классическим методом g(t) крайне неудобно, но так как δ(t) формально является производной , то найти её можно из соотношения g(t)=h(0)δ(t) + dh(t)/dt.

Для экспериментального определения этих характеристик приходится действовать приближённо, то есть создать точное требуемое воздействие невозможно.

На вход падают последовательность импульсов, похожих на прямоугольные:

t_ф – длительность переднего фронта (время нарастания входного сигнала);

t_и – длительность импульса;

К этим импульсам предъявляют определённые требования:

а) для переходной характеристики:

- t_паузы должно быть таким большим, чтобы к моменту прихода следующего импульса переходный процесс от окончания предыдущего импульса практически заканчивался;

- t_и должно быть таким большим, чтобы переходный процесс, вызванный возникновением импульса, тоже практически успевал заканчиваться;

- t_ф должно быть как можно меньше (так, чтобы за t_ср состояние цепи практически не менялось);

- X_m должна быть с одной стороны такой большой, чтобы с помощью имеющейся аппаратуры можно было бы зарегистрировать реакцию цепи, а с другой: такой маленькой, чтобы исследуемая цепь сохраняла свои свойства. Если всё это так, регистрируют график реакции цепи и изменяют масштаб по оси ординат в X_m раз (X_m =5В, ординаты поделить на 5).

б) для импульсной характеристики:

t_паузы – требования такие же и к X_m – такие же, к t_ф требований нет (потому что даже сама длительность импульса t_ф должна быть такой малой, чтобы состояние цепи практически не менялось. Если всё это так, регистрируют реакцию и изменяют масштаб по оси ординат на площадь входного импульса .

Итоги по классическому методу

Основным достоинством является физическая ясность всех используемых величин, что позволяет проверять ход решения с точки зрения физического смысла. В простых цепях удаётся очень легко получить ответ.

Недостатки: по мере возрастания сложности задачи быстро нарастает трудоёмкость решения, особенно на этапе расчёта начальных условий. Не все задачи удобно решать классическим методом (практически никто не ищет g(t), и у всех возникают проблемы при расчёте задач с особыми контурами и особыми сечениями).

До коммутации , .

Следовательно, по законам коммутации u_c ₁ (0) = 0 и u_c ₂ (0) = 0, но из схемы видно, что сразу после замыкания ключа: E= u_c ₁ (0)+u_c ₂ (0).

В таких задачах приходится применять особую процедуру поиска начальных условий.

Эти недостатки удаётся преодолеть в операторном методе.

6. Расчет реакции линейной цепи на входное воздействие произвольного вида с применением временных характеристик цепи

Раньше мы рассматривали два вида входного воздействия:

1) x_вх = δ(t)-на входе будет импульсная характеристика g(t);

2) x_вх = 1(t)-переходная характеристика h(t).

При произвольном заданном виде входного воздействия, в линейной цепи тоже можно найти реакцию. Для этого годятся и g(t) и h(t) и передаточная функция H(p), но в зависимости от формы входного сигнала, сложности цепи и того математического аппарата, которым располагаешь, более удобно будет применить какую-то одну из этих характеристик.

Рассмотрим применение переходной характеристики h(t):

1) На входе действуют прямоугольным импульсом

Воспользуемся принципом наложения и представим этот импульс в виде двух скачков U_m 1(t) и -U_m 1(t-t_u ).

Если нам известна переходная характеристика на h(t), то реакция на каждый скачок записывается очень просто U_m h(t) и -U_m h(t-t_u ) (h(t)=1-e^- ^t ^/ ^τ ).

Вся реакция определяется сложением этих двух графиков.

Т.е. для 0≤t<t_u U_вых (t)=U_m h(t), t≥t_u U_вых (t)=U_m h(t)–U_m h(t-t_u ).

2) Входной сигнал – функция, которая в некоторые моменты времени изменяется скачком, а между этими моментами постоянно.

И в этом случае задача решается просто: раскладываем входной сигнал на совокупность скачков и записываем для каждого интервала времени свое выражение для реакции:

0≤t<10^-3 x_вых =5∙h(t)

10^-3 ≤t<2∙10^-3 x_вых =5∙h(t)+10∙h(t-10^-3 )

t≥2∙10^-3 x_вых =5∙h(t)+10∙h(t -10^-3 ) -18∙h(t -2∙10^-3 ).

Все такие задачи решаются с помощью h(t).

1) Входной сигнал в некоторый момент времени имеет скачки, а между

этими моментами времени плавно изменяется по тому-то закону (или вообще плавно изменяется без скачков).

Представим себе, что этот сложный сигнал приближенно м.б. составлен из нескольких скачкообразных воздействий (первое воздействие имеет амплитуду x_вх (0) и возникает в момент t=0, второе воздействие возникает в некоторый момент t₁ и имеет амплитуду x_вх (t₁ )-x_вх (0)=∆x_вх (t₁ ), третий сигнал поступает в момент t₂ и имеет амплитуду ∆x_вх (t₂ ) и т.д.). Значит можно написать, что для некоторого момента t:

x_вх (t)≈x_вх (0)1(t)+∑∆x_вх (t_j )1(t-t_j ) (*).

В сумме учитывая все те ступеньки, которые возникли до нашего момента времени t. Если ступеньки брать помельче, выражение будет получаться поточнее, но все равно приближенно. Получим теперь точное выражение. В нашем случае:

x_вых (t)≈x_вх (0)h(t)+∑∆x_вх (t_j )∙h(t-t_j ) (**).

Известно, что ∆x_вх (t_j )/∆t_j ≈x(t_j ) и тогда (**) перепишется x_вых (t)≈x_вх (0)∙h(t)+∑x_вх ′(t_j )∆t_j h(t-t_j ). Уменьшая ∆t_j до dt_j вместо суммы получим интеграл: (для удобства записи t_j →λ)

Если бы функция имела скачки не только в момент 0, но и в какие-то другие моменты. Пришлось бы для каждого интервала времени в котором функция непрерывна, записывать свои выражения отличающиеся друг от друга наличием реакции на скачки случившиеся до рассмотрения момента времени t.

Пример: Есть h(t)=0,5e^-500 ^t . Надо найти реакцию цепи на входное воздействие.

Описывает входное воздействие аналитически. В нашем случае можно считать, что в интервале от 0 до 10^-3 U_вх1 (t)=a+b∙t:

30=10+b∙10^-3 ; a=10; b=2∙10⁴ .

U_вх2 (t)=15+A∙e^- ^t ^/ ^τ ; τ=8∙10^-4 ; t/τ=10^-3 /8∙10^-4 ;

U_вх2 (t=10^-3 )=5=15+A∙e^-1,25 ; A≈-30.

Теперь для каждого интервала времени записываем свое выражение:

0≤t<10^-3

Берем интеграл, приводим подобные члены, строим графики. Но в рамках курса ТОЭ РГРТУ требуется ответ до состояния

t≥10^-3

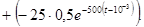
Применение импульсных характеристик

Известно, что

1) g(t)= ^-1 {H(p)},

2) x_вых (p)=x_вх (p)H(p),

3) =,

Пусть , ,

тогда =^-1 =

Фактически это есть другая форма интеграла Дюамеля, которая может быть получена используя связь g(t) и h(t). Порядок применения получения выражения такой же, но при численном нахождении интеграла удобней использовать собственно интеграл Дюамеля.

Применение передаточной функции

Если известно H(p) и x_вх (t), можно записать изображение x_вх (p), вычислить x_вых (p)=H(p)x_вх (p) и перейти к оригиналу.

Особенно удобно применять H(p)тогда, когда x_вх (t) имеет простой вид, позволяющий легко записать изображение x_вх (p) либо сразу для всего сигнала, либо разложение его на более простые компоненты и воспользовавшись принципом положения.

Например:

x_вх (t)=10e^-100 ^t

, ,

, , ,

, ,

Этот входной сигнал можно представить в виде совокупности двух более простых. Тогда

1) Для0 ≤t<10^-2

2) Для t≥10^-2 , t<2∙10^-2

3) .

Теперь умножая на H(p) находим изображающие реакции и затем переходим к оригиналу.

Список используемых источников

1. Основы теории цепей. Учебник для вузов./ Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов.-5-е изд. перераб.-М.: Энергоатомиздат, 1989. 528 с.

2. В.П. Попов. Основы теории цепей. Учебник для вузов. -М.: Высшая школа, 1985. 496 с.

3. Теория электрических цепей: Методические указания к лабораторным работам / Рязан. гос. радиотехн. акад.; Сост.: С.М. Милюков, В.П. Рынин; Под ред. В.П. Рынина. Рязань, 2002. 16 с.,2004. 20 с. (№3282, №3624)

4. Электротехника и электроника: Методические указания к расчетно-графической работе / Рязан. гос. радиотехн. акад.; Сост. Г.В. Спивакова. Рязань, 2005. 16 с. (№3665)

5. М.Р. Шебес. Теория линейных электрических цепей в упражнениях и задачах. М.: Высшая школа, 1990. 528 с.

6. Матханов П.Н. Основы анализа электрических цепей. Нелинейные цепи: Учеб. для электротехн. спец. вузов. –2-е изд., перераб. и доп. –М.: Высш. шк., 1986. –352 с.

7. Каплянский А.Е. и др. Теоретические основы электротехники. Изд. 2-е. Учеб. пособие для электротехнических и энергетических специальностей вузов. –М.: Высш. шк., 1972. -448 с.

8. Теоретические основы электротехники. Т. 1. Основы теории линейных цепей. Под ред. П.А. Ионкина. Учебник для электротехн. вузов. Изд. 2-е, перераб. и доп. –М.: Высш. шк., 1976. –544 с.