КУРСОВАЯ РАБОТА
На тему:
"Рассеяние волн в задаче о маскировке объектов методом волнового обтекания"
Минск, 2010 г.
Введение
У людей с давних времён есть желание замаскироваться, а то и вовсе стать невидимым для окружающих. И с недавних пор это может стать возможным с помощью метода волнового обтекания. Основной целью курсовой работы является изучение метода рассеяния волн в задаче о маскировке объектов методом волнового обтекания, рассмотрение основных характеристик и свойств маскирующих покрытий, изучение их классификации. А также, как дополнение, рассмотрение быстрого преобразования Фурье и его применения в задаче о рассеянии. Задача курсовой работы заключается в овладении методом решения задачи о рассеянии и изучении маскирующих оболочек.
Под маскировкой или скрытием методом волнового обтекания следует понимать такое преобразование фронта волны маскирующей оболочкой, что он огибает скрываемый объект. В реальных условиях невозможно добиться идеальной маскировки, но принципиально возможно сведение потерь и рассеяния к пренебрежимо малым для поставленной задачи значением. А в задаче маскировки таких сравнительно небольших объектов, как тело человека, ракет, самолётов, и прочей военной техники, учитывая маловероятность отклика радаров на большое для идеальных моделей, но значительно меньшее, чем у объектов без маскирующих оболочек, рассеяние, при желании распределённое во всех направлениях, делает их скрытие очень перспективной и востребованной задачей. Учитывая характер явления, его преимущественной областью применения является военно-стратегическая.
1. Решение задачи о рассеянии
1.1 Решение задачи о рассеянии в общем случае
В общем случае задача о рассеянии ставится следующим образом. На некоторый объект произвольной формы с диэлектрической проницаемостью 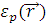 и объемом V падает электромагнитная волна в направлении распространения и объемом V падает электромагнитная волна в направлении распространения 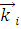 и с колебаниями электрического вектора в направлении и с колебаниями электрического вектора в направлении 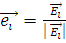 (рис. 1.1). Волна движется в пространстве с диэлектрической проницаемостью (рис. 1.1). Волна движется в пространстве с диэлектрической проницаемостью 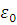 . После рассеивания и поглощения результирующая волна имеет направление распространения . После рассеивания и поглощения результирующая волна имеет направление распространения 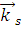 и колебания электрического вектора в направлении и колебания электрического вектора в направлении 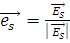 . .
Для вычисления рассеянных электромагнитных полей и сечения рассеяния необходимо сначала записать общее решение для поля внутри рассеивающего тела, поля рассеянных волн и падающего поля, а затем вычислить неизвестные постоянные коэффициенты (спектральные амплитуды) с помощью граничных условий.
1.2 Решение задачи о рассеянии в общем случае
Решение задачи о рассеянии в общем случае заключается в нахождении сечения рассеяния.
Запишем электрическое поле падающей волны следующим образом:
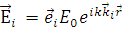 , (1.2.1) , (1.2.1)
где 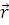 = =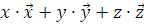 – вектор описывающие местоположение относительно базиса ( – вектор описывающие местоположение относительно базиса (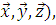 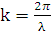 – волновое число. Рассеянное поле вдали от рассеивателя может быть описано сферической волной: – волновое число. Рассеянное поле вдали от рассеивателя может быть описано сферической волной:
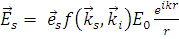 , (1.2.2) , (1.2.2)
где r – расстояние от рассматриваемой точки до точки рассеяния,
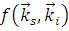 – амплитуда рассеяния, зависящая от направления рассеянной – амплитуда рассеяния, зависящая от направления рассеянной 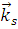 и падающей и падающей 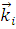 волн. волн.
Магнитное поле падающей волны вычисляется из уравнений Максвелла и имеет следующий вид:
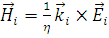 , (1.2.3) , (1.2.3)
где η=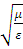 есть волновое сопротивление (импеданс). есть волновое сопротивление (импеданс).
Вектор Умова-Пойтинга, который определяет поток мощности поля через единицу поверхности, записывается следующим образом:
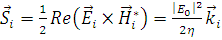 . (1.2.4) . (1.2.4)
Рассуждаем так же и для рассеянной волны. Магнитное поле рассеянной волны по определению следующее
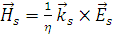 , (1.2.5) , (1.2.5)
а вектор Умова-Пойтинга рассеянной волны
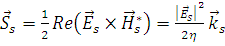 , 1.2.6. , 1.2.6.
Подставляя выражение (1.2.2) в (1.2.6), получаем
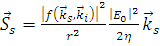 . (1.2.7) . (1.2.7)
В сферической системе координат возьмём дифференциал телесного угла в направлении рассеяния (рис 1.2)
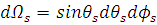 . (1.2.8) . (1.2.8)
На расстоянии r
, от рассеивающей точки, площадь поверхности ограниченной дифференциалом телесного угла 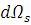 записывается следующим образом: записывается следующим образом:
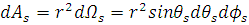 . (1.2.9) . (1.2.9)
Тогда дифференциал рассеянной мощности через площадку 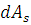 принимает следующий вид: принимает следующий вид:
 . (1.2.10) . (1.2.10)

Дифференциал телесного угла в сферических координатах r, θs
, φs
Теперь, подставляя (1.2.7) в (1.2.10) получим следующее выражение для мощности, рассеянной в элемент телесного угла:
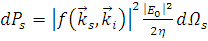 . (1.2.11) . (1.2.11)
Разделив левую и правую части выражения (1.2.11) на вектор Умова-Пойтинга для падающей волны (1.2.4), получим
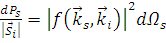 . (1.2.12) . (1.2.12)
Размерность последнего соотношения является размерностью площади. 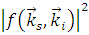 называется дифференциальным сечением рассеяния и обозначается как называется дифференциальным сечением рассеяния и обозначается как 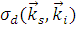 . .
А интегрирование 1.2.12, в свою очередь, даёт
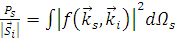 . (1.2.13) . (1.2.13)
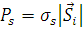 , (1.2.14) , (1.2.14)
где 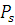 – рассеянная мощность, а – рассеянная мощность, а 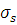 – сечение рассеяния. – сечение рассеяния.
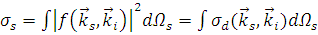 . (1.2.15) . (1.2.15)
1.2 Решение задачи о рассеянии на цилиндре
Решается задача о нахождении полей на таком удалении от точек рассеяния, что фронт распространения волн этих полей можно считать плоскостью. Найдём для этого сперва общее решение, характеризующее бесконечно длинный цилиндр, а затем подставим в решение граничные условия, обобщив его тем самым на цилиндр длинны L.
Пусть поле падающих волн задаётся выражением:
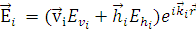 , (1.2.1) , (1.2.1)
где 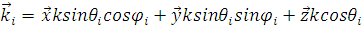 (см. рис. 2.1), падающая волна раскладывается в суперпозицию двух поляризаций – горизонтальной линейной и вертикальной линейной, а (см. рис. 2.1), падающая волна раскладывается в суперпозицию двух поляризаций – горизонтальной линейной и вертикальной линейной, а 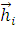 и и 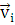 горизонтальный и вертикальный вектора поляризации. горизонтальный и вертикальный вектора поляризации.
Падающая волна также может быть представлена в виде векторных цилиндрических волн, т.е. следующим образом:
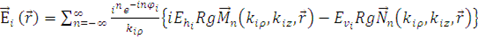 . (1.2.2) . (1.2.2)

Цилиндр высоты L, радиуса a
и проницаемости 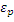
Общее решение будет состоять из выражений для рассеянного поля и поля внутри цилиндра объединённых граничными условиями. Запишем теперь выражения, определяющие рассеянное и внутренне поля с точностью до неизвестных коэффициентов 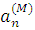 , , 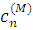 , , 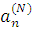 , ,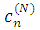 на оговоренном ранее расстоянии от точки рассеяния на оговоренном ранее расстоянии от точки рассеяния
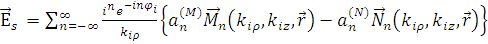 , (1.2.3) , (1.2.3)
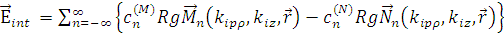 , (1.2.4) , (1.2.4)
где 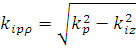 , , 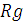 – символ, с помощью которого обозначается конфигурация функций Бесселя и Ханкеля для величин, перед которыми он стоит, а – символ, с помощью которого обозначается конфигурация функций Бесселя и Ханкеля для величин, перед которыми он стоит, а 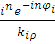 – коэффициенты, получаемые с использованием преобразования Фурье от выражения (1.2.1) – коэффициенты, получаемые с использованием преобразования Фурье от выражения (1.2.1)
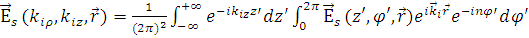 , ,
известны для такого приближения.
Граничные условия задаются равенствами:
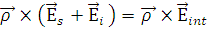 , (1.2.5) , (1.2.5)
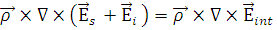 , (1.2.6) , (1.2.6)
из которых можно путём преобразований получить следующие выражения
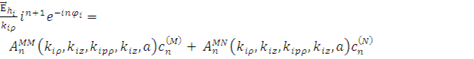 , (1.2.7) , (1.2.7)
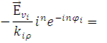
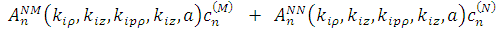 , (1.2.8) , (1.2.8)
которые задают зависимость неизвестных коэффициентов 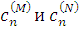 из выражения для внутреннего поля (1.2.4) от направлений распространения из выражения для внутреннего поля (1.2.4) от направлений распространения 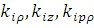 , полей , полей 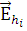 , , 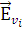 , координаты , координаты 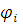 и и 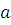 – радиуса цилиндра. Таким образом, поле – радиуса цилиндра. Таким образом, поле 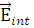 определено, т. к. коэффициенты определено, т. к. коэффициенты 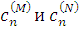 могут быть легко получены из (1.2.7), (1.2.8). могут быть легко получены из (1.2.7), (1.2.8).
Поле, образовавшееся после рассеяния падающего поля на цилиндре высоты L, в точках находящихся на достаточном для нашего приближения удалении определим путём интегрирования по конечной поверхности цилиндра, исключая граничные точки, используя формулу
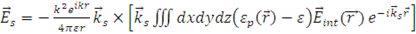 . (1.2.9) . (1.2.9)
После подстановки (1.2.4) в (1.2.9) и выполнения интегрирования по dz в интервале (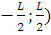 и по dφ в интервале (0; 2π) получим следующее выражение для поля рассеянных волн: и по dφ в интервале (0; 2π) получим следующее выражение для поля рассеянных волн:
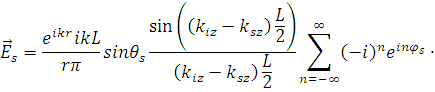
{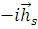 [ [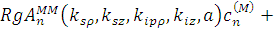
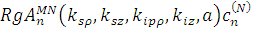 ] ]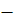
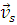 [ [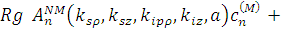
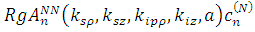 ]}. (1.2.10) ]}. (1.2.10)
Итак, нами были найдены поля 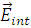 и и 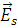 . Однако есть несколько ограничений для полученных решений. Во-первых, следует иметь в виду, что такое решение непригодно вблизи точек рассеяния. Во-вторых, амплитудные коэффициенты, которые использовались в уравнениях (2.3), (2.4), были взяты готовыми, как известные для плоских волн. В общем случае их нужно рассчитывать отдельно для каждой конкретной задачи, используя преобразование Фурье, как это делается в работе [9]. . Однако есть несколько ограничений для полученных решений. Во-первых, следует иметь в виду, что такое решение непригодно вблизи точек рассеяния. Во-вторых, амплитудные коэффициенты, которые использовались в уравнениях (2.3), (2.4), были взяты готовыми, как известные для плоских волн. В общем случае их нужно рассчитывать отдельно для каждой конкретной задачи, используя преобразование Фурье, как это делается в работе [9].
1.3 Быстрое преобразование Фурье
Преобразование Фурье используется при решении задачи о рассеянии с целью нахождения амплитудных коэффициентов необходимых для описания волны. Характер последних, как уже упоминалось, зависит от того в каком приближении мы рассматриваем поставленную задачу. Суть применения преобразования Фурье заключается в разбиении произвольной волны на элементарные плоские волны. Таким образом, получаем амплитудные коэффициенты, стоящие как множители перед рядом, в виде которого представляется волна. Затем можно подставить граничные условия в полученное выражение, что позволяет выразить неизвестные 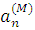 , , 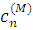 , , 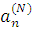 , ,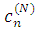 , как, например, в (1.2.3), (1.2.4). Затем, проведя обратное преобразование Фурье, получим представление искомой волны, удовлетворяющее задаче. , как, например, в (1.2.3), (1.2.4). Затем, проведя обратное преобразование Фурье, получим представление искомой волны, удовлетворяющее задаче.
Быстрое преобразование Фурье (БПФ) – это реализация обычного (дискретного) преобразования Фурье (ДПФ), но с намного меньшим количеством операций n=Nlog2
N, где N – размер строки данных, в отличие от n=N2
в ДПФ. В БПФ используются исключительно N, являющиеся степенями двойки. Если N не является степенью двойки, то его дополняют нолями до ближайшей из степеней.
Для осуществления БПФ можно использовать лемму Даниельсона-Ланкзоса, которая разбивает ряд ДПФ
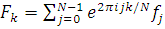 , (1.3.1) , (1.3.1)
где 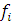 – исходная функция, на две суммы – по чётным и нечётным индексам j: – исходная функция, на две суммы – по чётным и нечётным индексам j:
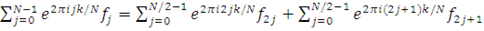 . (1.3.2) . (1.3.2)
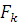 = =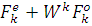 , (1.3.3) , (1.3.3)
где 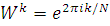 . Это и есть лемма Даниельсона-Ланкзоса [2]. Она подходит для осуществления как прямого БПФ, так и обратного. . Это и есть лемма Даниельсона-Ланкзоса [2]. Она подходит для осуществления как прямого БПФ, так и обратного.
В массиве данных 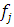 сперва следует произвести нумерацию элементов в двоичном виде, а затем пересортировать массив, заменяя каждый элемент элементом с обратным двоичным индексом. Полученная в результате таких перестановок последовательность после преобразования по формуле (1.3.3) задаёт искомую функцию. сперва следует произвести нумерацию элементов в двоичном виде, а затем пересортировать массив, заменяя каждый элемент элементом с обратным двоичным индексом. Полученная в результате таких перестановок последовательность после преобразования по формуле (1.3.3) задаёт искомую функцию.
Существуют также и другие алгоритмы БПФ, как, например в [10], но они в отличие от леммы Даниельсона-Ланкзоса не выполняют как прямое, так и обратное преобразование Фурье.
2. Скрытие материальных объектов методом волнового обтекания
2.1 Основополагающие идеи
Исторически первенство в идее и моделировании скрытия (английский термин cloaking) методом волнового обтекания принадлежит Дж. Пендри и его коллегам [3]. Они предложили принципиально новый метод маскировки, суть которого заключается в преломлении волн в маскирующей оболочке так, что они огибают скрытый в оболочке объект и на выходе из неё остаются такими же, какими в неё попадали. В результате поле выглядит так, как если бы на пути его распространения оно не встречало никаких препятствий.
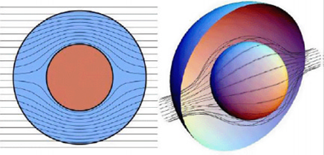
Траектории лучей в маскирующей оболочке
Чтобы наблюдатель не заметил никаких неоднородностей необходимо выполнение и следующего условия – оптическая длинна пути каждого луча в оболочке должна быть такой же, как если бы он распространялся прямолинейно в свободном пространстве. Для достижения такого эффекта для оболочки рассчитывают определённую конфигурацию параметров – диэлектрической и магнитной проницаемостей 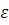 и и 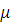 . .
Для расчета параметров маскирующего покрытия Пендри и его коллеги предложили использовать следующий приём: внутри некоторой области пространства (вакуума) создать включённую подобласть искривлённой метрики (в которой непосредственно и предполагается спрятать объект) при помощи преобразования координат.
Например, такого как в их работе [3].
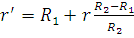 , , 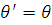 , , 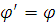 . (2.1.1) . (2.1.1)
Преобразование (2.1.1) переводит шар радиуса 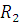 в шаровой слой в шаровой слой 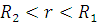 . .
Исходя из того, что уравнения Максвелла инвариантны преобразованиям координат [4], поле падающих волн ведёт себя в искривлённом пространстве таким же образом как и в исходном. Тензоры 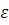 и и 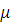 диэлектрической и магнитной проницаемостей также могут быть найдены. В [3] получены следующие диагональные элементы тензоров диэлектрической и магнитной проницаемостей также могут быть найдены. В [3] получены следующие диагональные элементы тензоров 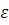 и и 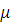 : :
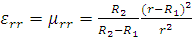 , (2.1.2) , (2.1.2)
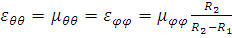 , (2.1.3) , (2.1.3)
Распределение параметров (2.1.2), (2.1.3) будут искривлять прямой луч также как и преобразования (2.1.1) искривляют прямую линию, пересекающую шар с радиусом r < 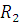 . Параметры . Параметры 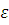 и и 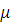 также могут быть выражены через метрический тензор искривлённого пространства gik
. также могут быть выражены через метрический тензор искривлённого пространства gik
.
Сами рассеянные поля находят решая задачу о рассеянии на маскирующей оболочке, где, как уже упоминалось, используется БПФ. Графики распределения нормированной амплитуды электрического поля (2.2.1, 2.3.1) строят по решению, полученному в задаче о рассеянии.
В связи с тем, что преобразования метрики не затрагивают временной составляющей, фазы каждого луча в оригинальной и преобразованной системах будут равны между собой.
Таким образом, для маскировки обтеканием нужно использовать анизотропные градиентные материалы с компонентами проницаемостей меньшими единицы, или – в некоторых случаях – отрицательными. Тот факт, что в анизотропной среде отсутствуют двулучепреломление и не изменяется поляризация попадающего в неё излучения объясняется равенством 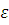 и и 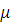 . Действительно, если речь идёт о преобразовании вакуума, то в нём . Действительно, если речь идёт о преобразовании вакуума, то в нём 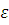 = =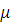 =1. =1.
Можно заметить, что к скрытию путём волнового обтекания могла бы приводить и антигравитация. Антигравитация, исходящая от какого либо тела, вызывает такие преобразования метрики пространства, что геодезические линии как бы раздвигаются.
Тот же принцип движения луча по искривлённой траектории объясняет и такое явление как мираж. Существенное отличие в температурах воздуха у поверхности земли и в более высоких слоях вызывает различие показателей преломления, вследствие чего свет распространяется не прямолинейно, а по кривой, и мы можем видеть объекты, расположенные за линией горизонта.
2.2 Свойства маскирующих покрытий и требования, предъявляемые к ним
Первое моделирование обтекания было проведено Каммером С.А. [5] в бесконечно длинной цилиндрической оболочке кругового сечения. Картина взаимодействия линейно поляризованной волны, вектор 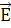 которой параллелен оси цилиндра, с пространственно неоднородными компонентами проницаемостей покрытием показана на рисунке 2.2.1а. В этой модели были рассмотрены различные приближения. которой параллелен оси цилиндра, с пространственно неоднородными компонентами проницаемостей покрытием показана на рисунке 2.2.1а. В этой модели были рассмотрены различные приближения.
Реальные покрытия имеют слоистую структуру, т.е. являются дискретными, что вызывает рассеяние, из-за которого траектории лучей вне оболочки перестают быть прямолинейными (рис. 2.2.1 б).
Идеальные параметры, использованные при построении графика 2.2.1а можно упростить. Если вектор 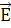 падающей волны параллелен оси цилиндра z, то задача становится двумерной и z – компоненты проницаемостей можно положить постоянными. Результат использования таких параметров отражен в графике 2.2.1в. падающей волны параллелен оси цилиндра z, то задача становится двумерной и z – компоненты проницаемостей можно положить постоянными. Результат использования таких параметров отражен в графике 2.2.1в.
В маскирующем покрытии также присутствует частотная дисперсия 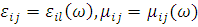 , вследствие чего оно может быть полностью эффективным только на одной частоте, для которой компоненты проницаемостей имеют нужный вид. Ясно что чем меньше составляющие спектра поглощения оболочки в её рабочем диапазоне, тем лучше. Но поглощение в свою очередь зависит и от дисперсии. Так следствием из соотношений Крамерса-Кронига является большое поглощение в диапазоне частот, в котором эта среда проявляет сильные изменения дисперсии. Таким образом, чем более плавный вид имеют зависимости , вследствие чего оно может быть полностью эффективным только на одной частоте, для которой компоненты проницаемостей имеют нужный вид. Ясно что чем меньше составляющие спектра поглощения оболочки в её рабочем диапазоне, тем лучше. Но поглощение в свою очередь зависит и от дисперсии. Так следствием из соотношений Крамерса-Кронига является большое поглощение в диапазоне частот, в котором эта среда проявляет сильные изменения дисперсии. Таким образом, чем более плавный вид имеют зависимости 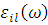 и и 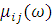 , тем меньше поглощение и тем ближе к идеалу эффект маскировки. , тем меньше поглощение и тем ближе к идеалу эффект маскировки.

Распределение нормированной амплитуды электрического поля вблизи цилиндрической маскирующей оболочки
2.3 Разнообразие форм маскирующих покрытий
Сейчас скрытие уже теоретически осуществимо на оболочках произвольной двумерной формы, а именно в сечении трёхмерной модели. Рассмотрим их классификацию. Изначально рассматриваемый метод, как уже упоминалось, базировался на сферической оболочке (см. гл. 2 § 1). Дальнейшее развитие метода, как и следовало ожидать, привело к появлению многих других форм.
Одно из простейших покрытий с формой эллиптического цилиндра рассмотрено в работе [6].

Распределение нормированной амплитуды электрического поля для различных углов падения излучения на эллиптическую оболочку: (а) 0°, (б) 90°, (в) 30°, (г) 45°
Для расчета его параметров используется линейное преобразование координат эллиптического цилиндра 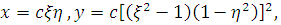 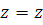 , сжимающее сплошной эллиптический цилиндр в цилиндр с полостью: , сжимающее сплошной эллиптический цилиндр в цилиндр с полостью:
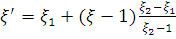 , , 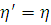 , , 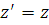 . (2.3.1) . (2.3.1)
Направление падающего излучения для такой оболочки не безразлично из-за меньшей степени симметрии чем, например, у сферы. Из рисунка 2.3.1 видно, что поле после прохождения препятствия имеет наиболее близкую исходному структуру при нулевом угле падения излучения.
Произвольный цилиндр – оболочка-цилиндр с произвольным сечением. В общем случае не существует преобразования, переводящего произвольную односвязную область в подобную ей двусвязную. В таком случае 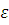 и и 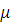 задают отдельно для каждой подобласти и используют отдельное преобразование для каждой из них. Например, цилиндрическая оболочка квадратного сечения (рис. 2.3.2), параметры которого рассчитаны в [7]. задают отдельно для каждой подобласти и используют отдельное преобразование для каждой из них. Например, цилиндрическая оболочка квадратного сечения (рис. 2.3.2), параметры которого рассчитаны в [7].
Для разбиения гладких оболочек на сектора их аппроксимируют кривыми Безье второго порядка. Эти кривые могут представлять собой любые канонические сечения (эллипсы, параболы, гиперболы), в зависимости от параметров. Для того чтобы достаточно точно аппроксимировать гладкую кривую, потребуется ломанная, состоящая из нескольких сотен отрезков, а кривых может понадобиться и две, как, например, для аппроксимации формы сердца. Параметрические уравнения кривой второго порядка по трём точкам 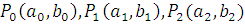 и трем параметрам (весам) и трем параметрам (весам) 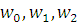 имеют вид [4]: имеют вид [4]:
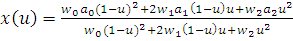 , (2.3.2) , (2.3.2)
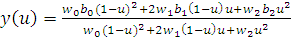 . (2.3.3) . (2.3.3)
Кроме уже исследованной сферической формы оболочки из трёхмерных моделей появилась ещё и модель эллипсоида вращения [8]. Пока решения задачи о рассеянии на оболочках произвольной формы не найдено, что связано с трудностями моделирования таких задач.

Координатное преобразование для цилиндрической оболочки квадратного сечения: для каждого сектора, выделенного на рисунке а, делается своё преобразование координат
Заключение
Итак, определившись с преобразованием координат для маскирующей оболочки, находим распределение её параметров 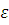 и и 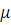 . Затем, разложив при помощи БПФ падающую волну на элементарные плоские волны, определяем амплитудные коэффициенты. Далее, используя граничные условия, вычисляем поля распределения рассеянных волн и волн внутри рассеивателя. Найденные поля и есть решение поставленной задачи, которое в дальнейшем может быть также представлено графически. Варьируя изначальные параметры оболочки . Затем, разложив при помощи БПФ падающую волну на элементарные плоские волны, определяем амплитудные коэффициенты. Далее, используя граничные условия, вычисляем поля распределения рассеянных волн и волн внутри рассеивателя. Найденные поля и есть решение поставленной задачи, которое в дальнейшем может быть также представлено графически. Варьируя изначальные параметры оболочки 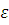 и и 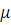 можно тем самым приближать модель к реальным условиям и рассчитывать сечение рассеяния с учетом потерь и дисперсии материала. можно тем самым приближать модель к реальным условиям и рассчитывать сечение рассеяния с учетом потерь и дисперсии материала.
В дальнейшем хотелось бы смоделировать решение для определённой оболочки, рассчитав её параметры, построить графики решений для этих оболочек. В дальней перспективе – написать программу, рассчитывающую сами поля, имея в качестве входящих значений параметры оболочки. Включить в неё функцию построения графиков решений. Подбирать оболочки и варьировать их параметры в поисках наиболее удачных.
Список литературы
1. Leung Tsang, Jin Au Kong, Kung-Hau Ding «Scattering of electromagnetic waves: theories and applications», «A Wiley-lnterscience» (2000);
2. W.H. Press, S.A. Teukolsky, W.T. Vetterling, Cambridge university press, New York (2002);
3. Pendry J B, Schurig D, Smith в R Science 312 1780 (2006);
4. А.Е. Дубинов, Л.А. Мытарева «Маскировки материальных объектов методом волнового обтекания», УФН (май 2010);
5. Cummer S A et al. Phys. Rev. E 74 036621 (2006);
6. Ma H et al. Phys. Rev. A 77 013825 (2008);
7. Rahm Met al. Photon. Nanostruct. Fund. Appl. 6 87 (2008);
8. Luo Y et al. Phys. Rev. B 78 125108 (2008);
9. A VNovitsky, «Matrix approach for light scattering by bianisotropic cylindrical particles», J. Phys.: Condens. Matter 19(2007);
10. Г. Нуссбаумер, «Быстрое преобразование Фурье и алгоритмы вычисления свёрток», Москва, «Радио связь» (1985);
|