Оренбургский государственный аграрный университет
Кафедра организации производства и моделирования экономических систем
Реферативно-прикладное исследование
Тема: "Моделирование систем массового обслуживания"
Выполнила:
студентка 44-эк группы
Проверила:
Спешилова Н.В.
Оренбург, 2004
Содержание
Цель работы
1. Теоретические аспекты исследования
1.1 Динамическое программирование
1.2 Сетевое планирование и управление
1.3 Моделирование систем массового обслуживания
1.4 Элементы теории игр в задачах моделирования экономических процессов
2. Элементы практического применения теории массового обслуживания
Выводы
Литература
Цель работы
Развитие современного общества характеризуется повышением технического уровня, усложнением организационной структуры производства, углублением общественного разделения труда, предъявлением высоких требований к методам планирования и хозяйственного руководства. В этих условиях только научный подход к руководству экономической жизнью общества позволит обеспечить высокие темпы развития народного хозяйства. Одним из необходимых условий дальнейшего развития экономической науки является применение точных методов количественного анализа, широкое использование математики. Одной из основных становится задача создания единой системы оптимального планирования и управления народным хозяйством на базе широкого применения математических методов и электронно-вычислительной техники в экономике.
В задачах моделирования экономических процессов используются такие методы, как:
1) динамическое программирование;
2) сетевое планирование и управление;
3) теория массового обслуживания;
4) теория игр.
Целью данного исследования является:
· ознакомление с теоретическими аспектами методов;
· рассмотрение на практике одного из них (моделирование систем массового обслуживания);
· на основе приведенного примера сделать соответствующие выводы.
1. Теоретические аспекты исследования
1.1 Динамическое программирование
Динамическое программирование представляет собой математический аппарат, позволяющий осуществлять оптимальное планирование многошаговых управляемых процессов и процессов, зависящих от времени. Экономический процесс называется управляемым, если можно влиять на ход его развития. Управлением называется совокупность решений, принимаемых на каждом этапе с целью влияния на ход процесса. В экономических процессах управление заключается в распределении и перераспределении средств на каждом этапе. Например, выпуск продукции – управляемый процесс, так как он определяется изменением состава оборудования, объемом поставок сырья, величиной финансирования и т. д. Совокупность решений, принимаемых в начале каждого года планируемого периода, по обеспечению предприятия сырьем, замене оборудования, размерам финансирования и т. д. Является управлением. Выпуск продукции надо спланировать так, чтобы избежать нежелательных эффектов (например, быстрый износ оборудования при использовании его на полную мощность). Необходимо предусмотреть мероприятия, обеспечивающие пополнение оборудования по мере изнашивания, т. е. по периодам времени. Последнее хотя и приводит к уменьшению выпуска продукции, но обеспечивает в дальнейшем возможность расширения производства. Таким образом, экономический процесс выпуска продукции можно считать состоящим из нескольких этапов (шагов), на каждом из которых осуществляется влияние на его развитие.
Началом этапа (шага) управляемого процесса считается момент принятия решения. Под этапом обычно понимают хозяйственный год. Однако динамическое программирование используется и в таких задачах, где время вообще не фигурирует.
Планируя многоэтапный процесс, исходят из интересов всего процесса в целом, т. е. при принятии решения на отдельном этапе всегда необходимо иметь в виду конечную цель.
Предметом динамического программирования являются задачи оптимального планирования, носящие динамический характер в том смысле, что при их решении приходится учитывать фактор времени или последовательность операций. Существенная особенность динамического программирования состоит в том, что решение любой задачи этим методом сводится к многоэтапному процессу нахождения оптимального решения. Это означает, что процесс поиска оптимального решения разбивается на относительно небольшие и, следовательно, легче поддающиеся решению подзадачи.
Методом динамического программирования решаются, например, задачи оптимального распределения капиталовложений, замены оборудования, оптимального управления запасами и многие другие.
Для большинства задач динамического программирования классические методы анализа или вариационного исчисления оказываются неэффективными, так как приводят первоначально поставленную задачу отыскания максимального значения функции к задаче, которая не проще, а сложнее исходной. Достоинством динамического программирования является то, что, используя поэтапное планирование, оно позволяет не только упростить решение задач, но и решить те из них, к которым нельзя применить методы математического анализа. Упрощение решения достигается за счет значительного уменьшения количества исследуемых вариантов, так как вместо того, чтобы один раз решать сложную многовариантную задачу, метод поэтапного планирования предполагает многократное решение относительно простых задач. Однако динамическое программирование имеет и свои недостатки. В отличие от линейного программирования, в котором симплексный метод является универсальным, в динамическом программировании такого метода не существует. Каждая задача имеет свои трудности, и в каждом случае необходимо найти наиболее подходящую методику решения. Недостаток динамического программирования также заключается в трудоемкости решения многомерных задач.
Большой вклад в разработку теории динамического программирования внес американский математик Р. Беллман. Ему принадлежит разработка основного функционального уравнения, которое является математическим выражением сформулированного им же одного из важных принципов динамического программирования – принципа оптимальности. Этот принцип состоит в следующем: оптимальное поведение обладает тем свойством, что каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения.
Модели динамического программирования могут содержать одну и более переменных. Увеличение количества переменных вызывает рост возможных вариантов решения. Возникает так называемая проблема размерности (или проклятие размерности, по выражению Р. Беллмана), которая является серьезным препятствием при решении задач динамического программирования средней и большой размерности.
1.2 Сетевое планирование и управление
Сетевое планирование и управление вознило в 1957 – 1958 г.г. под названием "метод критического пути" и метод PERT (метод оценки и прерсмотра планов). Система сетевого планирования и управления (СПУ) представляет собой комплекс графических и расчетных методов, организационных мероприятий с целью моделирования, анализа и оптимизации плана работ по проектированию или изготовлению некоторого изделия.
Методы сетевого планирования и управления предусматривают:
- представление планов в виде сети;
- определение календарных графиков;
- определение вероятных величин;
- возможность применения в различных условиях.
Метод сетевого планирования и управления пригоден как в промышленности, так и в сельском хлзяйстве.
Методы сетевого планирования и управления дают возможость:
1. заранее планировать все действия, которые необходимо предринять для достижения желаемого результата в будущем;
2. предсказать вероятное время выполнения;
3. улучшить план, если предсказанное время выполнения является недостаточно хорошим;
4. проверить ход выполнения работ по плану;
5. использовать инфомацию о ходе работ для своевременного планирования времени и затрат.
Основным плановым документом в системе СПУ является сетевой график (сетевая модель или просто сеть), представляющий собой безмасштабное графическое изображение планируемого процесса и отражающий взаимосвязь и последовательность входящих в него работ.
Особенность СПУ состоит в использовании новой, более совершенной формы представления плана, которая значительно облегчает его восприятие и упрощает процесс руководства работами. Сетевая модель дает больше информации, чем модели типа ленточных.
Объектом управления в системах СПУ является коллектив исполнителей, располагающий определенными материальными и денежными ресурсами и выполняющий комплекс работ, направленных на достижение конечного результата в установленные сроки.
Сетевые графики используют в строительстве, проектировании, в подготовке и освоении производства новых видов промышленной продукции, в создании новых программ для ЭВМ, при реконструкции и планово-предупредительном ремонте действующего оборудования, при установке и наладке ЭВМ, в планово-экономической работе предприятий. Впервые СПУ нашло применение в строительстве.
В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа. Граф – это схема, состоящая из заданных точек – вершин, соединенных определенной системой линий, которые также называются ребрами или дугами графа. Ребра могут быть ориентированными (тогда они называются дугами и снабжаются стрелками) и неориентированными. Пара вершин может соединяться более чем одним ребром и такие ребра называются кратными. Вершина может быть соединена ребром сама с собой, и такое ребро называется петлей. Имеется несколько типов графов: обыкновенный граф (рис. 1, а), мультиграф (рис. 1,б), ориентированный граф (рис.1,в) и др. граф без дуг, петель и кратных ребер называется обыкновенным. Если граф имеет кратные ребра, то он называется мультиграфом. Обыкновенный граф, у которого все ребра являются ориентированными, называется ориентированным.

Рис.1.
В основе сетевого графика лежит ориентированный граф. Одной из основных конструкций ориентированного графа является путь. Путь – это последовательность дуг, позволяющая пройти из одной вершины в другую и каждая дуга которой встречается не более одного раза. Замкнутый путь, соединяющий вершину с ней же самой, называется контуром. Понятие пути имеет важное значение в сетевом моделировании.
Сетевой график – это конечный плоский ориентированный граф без контуров, дуги которого имеют одну или несколько числовых характеристик.
В сетевом графике имеется два основных элемента – работа и событие. Работы соответствуют дугам графа, а события – вершинам. Работами называются любые процессы, действия, приводящие к достижению определенных результатов (событий). В сетевом графике может быть несколько разновидностей работ: действительная работа, ожидание, фиктивная работа. Действительной называется работа, требующая затрат времени и ресурсов. Ожиданием называется работа, которая требует затрат времени, но требует затрат ресурсов. Фиктивная работа отражает логическую связь между работами и не требует затрат времени и ресурсов. Действительные работы и ожидания изображаются на графике сплошными стрелками, фиктивные работы – пунктирными стрелками. Количественные показатели (время, стоимость, ресурсы), характеризующие работу, проставляются над стрелками (рис.2).
Событием называется результата произведенной работы. События изображаются кружками, внутри которых – номер события (рис.2).

Рис. 2.
Прежде чем использовать сетевой график как основной инструмент управления ходом работ, необходимо провести его анализ и оптимизацию. После этого осуществляется привязка сети к календарю, в результате чего создается план-график проведения работ, в котором указываются даты наступления событий, начала и окончания работ, величины резервов времени и т. д. Этот документ передается ответственным исполнителям, которые приступают к выполнению работ в соответствии с разработанным графиком. Сетевое моделирование находит широкое применение при планировании научно-исследовательских и проектно-конструкторских работ. Достоинством сетевых моделей является то, что они позволяют повысить эффективность планирования. При этом следует отметить, что несмотря на все преимущества методов СПУ, их нельзя считать окончательно сформировавшимися, а сетевые модели идеальными, поскольку они не исключают влияния субъективных оценок и не обеспечивают нахождение оптимального решения.
1.3 Моделирование систем массового обслуживания
Теория массового обслуживания впервые применялась в телефонии, а затем и в других областях хозяйственной деятельности.
Например, организация нормального процесса обслуживания покупателей связана с правильным определением следующих показателей: количества предприятий данного торгового профиля, численности продавцов в них, наличия соответствующих основных фондов, частоты завоза товаров, численности обслуживаемого населения, плотности обращаемости и потребности в соответствующих товарах. Если предположить, что предприятие располагает необходимыми основными фондами, торгует товарами, имеющимися в достаточном количестве, то и тогд а в процессе обслуживания остаются такие переменные величины, которые могут существенно повлиять на качество обслуживания. Надлежит, следовательно, выбрать такой оптимальный вариант организации торгового обслуживания населения, при котором время обслуживания будет минимальным, качество – высоким, не будет излишних народохозяйственных затрат. Математический аппарат теории массового обслуживания облегчает решение этой задачи.
Системы массового обслуживания (СМО) занимают важное место во многих сферах хозяйственной деятельности. Примерами СМО могут служить телефонные станции, ремонтные мастерские (заводы, базы, бригады), погрузочно-разгрузочные комплексы (порты, товарные станции), транспортные системы, автозаправочные станции, больницы, торговые точки, предприятия бытового обслуживания и т. д. Обрабатывающее предприятие, например машиностроительный завод, его цех, участок, станок также могут рассматриваться как СМО, обслуживающие поступающее сырье, заготовки, полуфабрикаты, комплектующие изделия.
 Каждая СМО имеет одно или несколько обслуживающих устройств, называемых каналами обслуживания (каналы связи, ремонтные бригады, краны, бензоколонки, продавцы, кассиры, парикмахеры, станки), и предназначена для обслуживания – выполнения потока заявок, требований, поступающих в систему большей частью в случайные моменты времени. Время обслуживания заявки также обычно случайно. Случайный характер потока заявок и времени обслуживания приводит либо к накоплению необслуженных заявок, либо к недогрузке СМО, простою ее каналов. Каждая СМО имеет одно или несколько обслуживающих устройств, называемых каналами обслуживания (каналы связи, ремонтные бригады, краны, бензоколонки, продавцы, кассиры, парикмахеры, станки), и предназначена для обслуживания – выполнения потока заявок, требований, поступающих в систему большей частью в случайные моменты времени. Время обслуживания заявки также обычно случайно. Случайный характер потока заявок и времени обслуживания приводит либо к накоплению необслуженных заявок, либо к недогрузке СМО, простою ее каналов.
 Задача теории массового обслуживания состоит в выработке рекомендаций по рациональному построению СМО, рациональной организации их работы и регулированию потока заявок с целью обеспечить более высокую эффективность обслуживания при малых затратах на создание и функционирование системы. Для этого теория массового обслуживания устанавливает зависимости между характеристиками потока заявок, числом и производительностью каналов обслуживания и "выходными" характеристиками СМО, описывающими результаты ее работы. Задача теории массового обслуживания состоит в выработке рекомендаций по рациональному построению СМО, рациональной организации их работы и регулированию потока заявок с целью обеспечить более высокую эффективность обслуживания при малых затратах на создание и функционирование системы. Для этого теория массового обслуживания устанавливает зависимости между характеристиками потока заявок, числом и производительностью каналов обслуживания и "выходными" характеристиками СМО, описывающими результаты ее работы.  Системы массового обслуживания делятся на две группы: СМО с отказами в обслуживании и СМО с ожиданием, или очередью. В СМО с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, получает "отказ" и сразу покидает систему, а не становится в очередь. Примерами системы с отказами могут служить система телефонной связи города, пошивочная мастерская, если нет "записи на очередь". Системы массового обслуживания делятся на две группы: СМО с отказами в обслуживании и СМО с ожиданием, или очередью. В СМО с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, получает "отказ" и сразу покидает систему, а не становится в очередь. Примерами системы с отказами могут служить система телефонной связи города, пошивочная мастерская, если нет "записи на очередь".
 В системах с ожиданием заявка, пришедшая в такой момент, когда все каналы заняты, не уходит, а становится в очередь и ждет освобождения канала. Системы с ожиданием делятся на системы с неограниченным ожиданием начала обслуживания, с ограничением времени ожидания и с ограничением длины В системах с ожиданием заявка, пришедшая в такой момент, когда все каналы заняты, не уходит, а становится в очередь и ждет освобождения канала. Системы с ожиданием делятся на системы с неограниченным ожиданием начала обслуживания, с ограничением времени ожидания и с ограничением длины  очереди. Обслуживание очереди (дисциплина очереди) может быть упорядоченным, т. е. строго в порядке поступления заявок, случайным, когда заявки обслуживаются в некотором случайном порядке, и с приорететами, когда в первую очередь обслуживаются заявки, обладающие некоторыми признаками. очереди. Обслуживание очереди (дисциплина очереди) может быть упорядоченным, т. е. строго в порядке поступления заявок, случайным, когда заявки обслуживаются в некотором случайном порядке, и с приорететами, когда в первую очередь обслуживаются заявки, обладающие некоторыми признаками. Принадлежность СМО к тому или другому виду зависит не только от характера системы, но и от приемлемой срочности обслуживания, наличия или отсутствия других СМО, оказывающих те же услуги, и других факторов. Принадлежность СМО к тому или другому виду зависит не только от характера системы, но и от приемлемой срочности обслуживания, наличия или отсутствия других СМО, оказывающих те же услуги, и других факторов.
 СМО называется разомкнутой, если поток заявок не зависит от ее функционирования. Обычно это бывает, когда заявок много и интенсивность потока заявок не изменяетмся заметно в результате работы СМО. Примерами разомкнутых СМО могут служить АТС, ремонтные бригады, мастерские, если заявок на ремонт так много, что работа СМО практически не влияет на их поступление. СМО называется замкнутой, если поток заявок зависит от функционирования системы. Так ремонтное предприятие должно рассматриваться как замкнутая СМО, если заявки поступают не очень часто и их поток зависит от пропускной способности предпрятия. СМО называется разомкнутой, если поток заявок не зависит от ее функционирования. Обычно это бывает, когда заявок много и интенсивность потока заявок не изменяетмся заметно в результате работы СМО. Примерами разомкнутых СМО могут служить АТС, ремонтные бригады, мастерские, если заявок на ремонт так много, что работа СМО практически не влияет на их поступление. СМО называется замкнутой, если поток заявок зависит от функционирования системы. Так ремонтное предприятие должно рассматриваться как замкнутая СМО, если заявки поступают не очень часто и их поток зависит от пропускной способности предпрятия.
Важшейшим показателем эффективности СМО является ее производительность, или пропускная способность, или среднее число заявок, которое система может обслужить за единицу времени, и относительная пропускная способность – отношение среднего числа заявок, обслуживаемых за единицу времени, к среднему числу поступивших за это время заявок.
Поток заявок характеризуется распределением заявок по времени. Исследование СМО весьма облегчается, если принимается простой поток заявок. В реальных условиях работы СМО поток заявок в большинстве случаев может считаться простейшим лишь на небольшом интервале времени, однако очень часто исследования СМО проводят, принимая поток заявок простейшим. Это объясняется, во-первых, простотой проведения анализа при таком потоке и, во-вторых, тем, что простейший поток очень напряженный, а следовательно, можно предполагать, что при реальном потоке эффективность СМО будет не хуже, чем дал анализ при простейшем потоке. Теория массового обслуживания позволяет проводить анализ СМО и при других, более сложных, чем простейший поток заявок, учитывающих нестационарность последействие, т. е. зависимость между заявками. Рассматриваются также схемы с учетом возможности выхода из строя каналов обслуживания, системы со взаимопомощью и дублированием каналов.
1.4 Элементы теории игр в задачах моделирования экономических процессов
При решении ряда практических задач в области экономики и организации сельского хозяйства приходится встречать случаи, когда две стороны преследуют противоположные цели, причем результат действий одной из сторон зависит от того, какой образ действий выберет другая сторона. Такие случаи называются конфликтными ситуациями. Конфликтные ситуации в различных областях человеческой деятельности изучает теория игр. Эта теория вырабатывает рекомендации по такому экономическому поведению противных сторон в процессе конфликтной ситуации, которое приводит к максимально возможному выигрышу.
Конфликтные ситуации, встречающиеся в реальной жизни, обусловливаются многочисленными факторами и являются весьма сложными. Чтобы можно было их изучать, необходимо отвлечься от всего второстепенного и сосредоточить внимание на анализе главных факторов, иначе говоря, надо формализовать реальную ситуацию и построить ее модель. Такую модель называют игрой. От реальной конфликтной ситуации игра отличается тем, что она ведется по предварительно оговоренным правилам и условиям. Стороны, участвующие в игре, называются игроками. В игре могут участвовать двое, тогда она называется парной. Если же в ней сталкиваются интересы многих лиц, то игра называется кооперативной. Ее участники могут образовывать постоянные или временные коалиции. При наличии двух коалиций кооперативная игра превращается в парную.
Игра представляет собой мероприятие, состоящее из ряда действий двух игроков, определяемых правилами игры. Частная возможная реализация этих правил называется партией. Результат или исход игры, к которому приводит совокупность принятых решений в процессе игры, называется выигрышем. В большинстве игр сумма выигрыша одного игрока равна сумме проигрыша другого, поэтому в любой их партии имеет место равенство:

Число 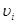 может быть положительным, отрицательным и равным нулю. При может быть положительным, отрицательным и равным нулю. При  - выигрыш, - выигрыш,  - проигрыш и - проигрыш и  - ничейный исход. Выигрыш или проигрыш не всегда имеет количественное выражение, например, в шахматной игре. В этих случаях результат выражают условными числами: выигрыш (+1), проигрыш (-1), ничья (0). Если один игрок выигрывает то, что проигрывает другой, то алгебраическая сумма выигрышей будет равна нулю. В этом случае имеет место игра с нулевой суммой. Бывает еще игра двух лиц с постоянной суммой. Бывает еще игра двух лиц с постоянной суммой. В этой игре два партнера непримиримо конкурируют из-за возможно большей доли разыгрываемой суммы. Посредством соответствующего преобразования такая игра может быть превращена в игру с нулевой суммой. - ничейный исход. Выигрыш или проигрыш не всегда имеет количественное выражение, например, в шахматной игре. В этих случаях результат выражают условными числами: выигрыш (+1), проигрыш (-1), ничья (0). Если один игрок выигрывает то, что проигрывает другой, то алгебраическая сумма выигрышей будет равна нулю. В этом случае имеет место игра с нулевой суммой. Бывает еще игра двух лиц с постоянной суммой. Бывает еще игра двух лиц с постоянной суммой. В этой игре два партнера непримиримо конкурируют из-за возможно большей доли разыгрываемой суммы. Посредством соответствующего преобразования такая игра может быть превращена в игру с нулевой суммой.
Развитие игры во времени сводится к ряду последовательных действий или вариантов принятия решений. Выбор одного из предусмотренных правилами игры вариантов называется ходом. Ходы делятся на личные и случайные. Личным ходом называется сознательный выбор одним из игроков одного из возможных в данной ситуации ходов и его осуществление. Случайным ходом называется выбор из ряда возможностей, осуществляемых не игроком, а каким-либо механизмом случайного выбора. Игры могут состоять из личных, случайных и смешанных ходов.
Теория игр может быть полезным инструментом планирования и управления сельскохозяйственным производством, а также прогнозирования. В задачах с конфликтными ситуациями ведется поиск хозяйственных стратегий, с помощью которых достигается максимально возможный (оптимальный) результат.
В любой игре важное значение имеет стратегия, под которой принимается совокупность правил, определяющих выбор при каждом личном ходе игрока, в зависимости от ситуации, сложившейся в процессе игры. В матричных играх применяются чистые и смешанные стратегии. Стратегии с компонентом, равным единице, называются чистыми стратегиями. Стратегии с отличными от единицы компонентами, представляющими вероятные ее доли, называются смешанными.
Задачей теории игр является нахождение решения игры, т. е. определение для каждого игрока его оптимальной стратегии и цены игры. Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш (или минимально возможный средний проигрыш) независимо от поведения противника. Ценой игры называется выигрыш (проигрыш), соответствующий оптимальным стратегиям игроков.
При выборе стратегий можно базироваться на различных принципах. В теории игр наилучшим принято считать поведение игроков, при котором каждый игрок предполагает, что его противник не глупее (тка называемый принцип разумности). В результате этого рекомендуется в качестве наилучшей стратегии выбирать ту, которая обеспечивает наибольший гарантированный выигрыш, т. е. выигрыш, не зависящий от действий потивника и который противник никак не может уменьшить. Элементы риска, а также просчеты и ошибки игроков во внимание не принимаются.
2. Элементы практического применения теории массового обслуживания
Рассмотрим систему массового обслуживания на примере обслуживания рабочих необходимым инвентарем.
Допустим, что в инвентарной кладовой работают два человека. Требуется определить, в какой степени они своевременно обеспечивают заявки на обслуживание, поступающие от рабочих; не обходятся ли простои рабочих в очереди дороже, чем дополнительное содержание еще одного или двух работников кладовой?
Таблица 1. – Расчет полного числа прихода рабочих в кладовую
| Число приходов в единицу времени (за 15 мин) |
Наблюдаемое число приходов, % |
Наблюдаемая частота приходов,% |
Полное число приходов рабочих (гр.1 * гр.2) |
Число приходов в единицу времени (за 15 мин) |
Наблюдаемоечисло приходов,% |
Наблюдаемая частота приходов,% |
Полное число приходов рабочих (гр.1 * гр.2) |
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
0
0
1
3
5
8
10
12
13
16
18
20
19
21
25
|
0
0
0,33
1,00
1,67
2,67
3,33
4,00
4,33
5,33
6,00
6,67
6,33
7,00
8,33
|
0
0
2
9
20
40
60
84
104
144
180
220
228
273
350
|
15
16
17
18
19
20
21
22
23
24
25
26
|
23
20
18
16
13
11
10
8
5
3
1
1
300
|
7,67
6,67
6,00
5,33
4,33
3,67
3,33
2,67
1,67
1,00
0,33
0,33
99,99
|
345
320
306
288
247
220
210
176
115
72
25
26
|
Для решения данной задачи необходимы прежде всего хронометражные замеры о потоке требований на обслуживание в единицу времени. Если хронометраж осуществляется в течение 10 дней каждые 15 минут за смену (кроме начала и конца рабочего дня), то за этот период времени было произведено 300 наблюдений (30 наблюдений, умноженное на 10 дней). Время наблюдений (T) составит 4500 мин (15 ×300). Причем таких промежутков, когда на склад никто не приходил или приходил только один рабочий, не наблюдалось, приход двух рабочих отмечался один раз, трех – три раза и т. д. (табл. 1).
Частота прихода двух рабочих при 300 наблюдениях равна 0,33 , трех – 1 , трех – 1 и т. д. и т. д.
Для определения среднего числа приходов в единицу времени ( ) исчисляется полное число приходов (N) как сумма произведений числа приходов (количества пришедших в кладовую рабочих) на наблюдаемое число приходов. ) исчисляется полное число приходов (N) как сумма произведений числа приходов (количества пришедших в кладовую рабочих) на наблюдаемое число приходов.
Таким образом, среднее число требований на обслуживание, т. е. среднее число приходов в единицу времени ( ), составит: ), составит:
 = =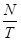 = = =0,903 чел. – мин. =0,903 чел. – мин.
Чтобы определить распределение вероятностей для длительности обслуживания при предположении, что закон распределения экспоненциальный, вычислим среднюю продолжительность одного обслуживания (Тобсл
); она равна 1,6 мин.
После этого можно установить интенсивность обслуживания ( ): ):
 = =  ; ;
 = =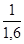 =0,625 чел. – мин. =0,625 чел. – мин.
В случае, когда  < < , увеличение очереди не возникает, так как удовлетворение требований происходит не ранее их поступления. В данном примере , увеличение очереди не возникает, так как удовлетворение требований происходит не ранее их поступления. В данном примере  > > (0,903>0,625) и в кладовой образуется очередь. (0,903>0,625) и в кладовой образуется очередь.
Точно определить величину очереди как случайную нельзя. Можно вычислить вероятность того, что в момент времени (t) очередь будет характеризоваться числом требований Pn
(t):
Pn
(t)=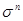 (1- (1- ); P0
(t) =(1- ); P0
(t) =(1- ); );  = =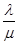 , ,
где P0
(t) – вероятность отсутствия очереди.
В тех случаях, когда   1, вероятность отсутствия очереди ( 1, вероятность отсутствия очереди ( 0
) обычно берется из графиков (в данном примере 0
) обычно берется из графиков (в данном примере  =1,445). =1,445).
Для построения таких графиков воспользуемся таблицей значений Р0
для различных значений  и n (n –количество кладовщиков в инструментальной кладовой). и n (n –количество кладовщиков в инструментальной кладовой).
Таблица 2. – Значения Р0
для различных значений  и n и n
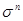 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
1
2
3
4
|
0,33 |
0,363
0,111
|
0,367
0,130
0,037
|
0,367
0,134
0,046
0,013
|
0,367
0,135
0,049
0,016
|
0,367
0,135
0,049
0,017
|
0,368
0,135
0,050
0,018
|
По данным табл.2 , в данном случае рассматривается многолинейная система, когда n 1 (количество кладовщиков превышает единицу). 1 (количество кладовщиков превышает единицу).
Определим среднее время ожидания (Tс
), которе складывается из среднего времени ожидания обслуживания в очереди (Тож
) и среднего времени обслуживания (Тобсл
):
Tс=
Тож
+ Тобсл.
В том случае, когда в системе работает n кладовщиков, среднее время ожидания в очереди определяется по формуле при n =2:
Тож
=  = = = 1,613; = 1,613;
Tс
= 1,613+1,6=3,213 мин;
при n=3
Тож
=  = = = 0,199; = 0,199;
Tс
= 0,199 +1,6 =1,799 мин;
при n=4
Тож
=  = = = 0,035; = 0,035;
Tс
= 0,035 +1,6 =1,635 мин и т. д.
Предположим, что у рабочего потери от простоев составляют 5, а содержание кладовщика – 4 ден. ед. в единицу времени. За период времени Т в систему поступает  Т заявок, т. е. 1,445Т заявок. Т заявок, т. е. 1,445Т заявок.
Потери вследствие простоя рабочих при различном числе кладовщиков, расходы на заработную плату кладовщиков, а также суммарные затраты и потери приведены в табл.3.
Таблица 3
| Количество кладовщиков |
Потери от простояРабочих |
Затраты на содержание кладовщиков |
Суммарные затраты и потери |
2
3
4
|
3,213*1,445*5Т=23,214 Т
1,799*1,445*5Т=12,998Т
1,635*1,445*5Т=11,813Т
|
8Т
12Т
16Т
|
31,214Т
24,998Т
27,813Т
|
Из табл. 3 следует, что экономически выгоднее в инструментальной кладовой иметь трех кладовщиков, поскольку суммарные затраты будут наименьшими (min 24,998Т).
Выводы
В процессе исследования были рассмотрены теоретические аспекты следующих методов программирования: динамическое программирование, сетевое планирование и управление, моделирование систем массового обслуживания, теория игр. Были рассмотрены основные задачи, решаемые с помощью этих методов, их основные достоинства и недостатки, а также основные понятия и теоремы. Динамическое программирование представляет собой математический аппарат, позволяющий осуществить оптимальное планирование многошаговых планируемых процессов и процессов, зависящих от времени. Предметом динамического планирования являются задачи оптимального планирования, носящие динамический характер в том смысле, что при их решении приходиться учитывать фактор времени или последовательность операций. Достоинством является то, что, используя поэтапное планирование, метод позволяет не только упростить решение задачи, но и решить те их них, к которым нельзя применить методы математического анализа. Недостатки: трудность решения многомерных задач, отсутствие универсального метода.
Сетевое планирование и управление представляет собой комплекс графических и расчетных методов, организационных мероприятий с целью моделирования, анализа и оптимизации плана работ по проектированию или изготовлению некоторого изделия. В основе лежит сетевой график, который является совершенной формой представления плана, которая значительно облегчает его восприятие и упрощает процесс руководства работами. Недостатки: не обеспечивает нахождение оптимального решения, не исключает влияния субъективных оценок.
Задача теории массового обслуживания состоит в выработке рекомендаций по рациональному построению систем массового обслуживания, рациональной организации их работы и регулирования потока заявок с целью обеспечения более высокой эффективности обслуживания при малых затратах на создание и функционирование системы. Метод дает оптимальный вариант обслуживания населения, при котором время обслуживания будет минимальным, качество – высоким, при этом не будет лишних затрат.
Теория игр – это теория математических моделей, интересы участников которых различны, причем они достигают своей цели различными путями. Теория игр дает рекомендации по рациональному образу действий участников многократно повторяющегося конфликта. Задачей теории игр является нахождение решения игры, т. е. определение для каждого игрока его оптимальной стратегии и цены игры.
В III главе приведена задача, которая решается с помощью теории массового обслуживания. Требовалось определить, своевременно ли обеспечиваются заявки на обслуживание, не обходятся ли простои рабочих в очереди дороже, чем затраты на содержание еще одного кладовщика. На основе хронометражных замеров определяется среднее число требований на обслуживание. Затем рассчитываются показатели среднего обслуживания одного работника и интенсивности обслуживания. Выясняем, что образуется очередь. Рассчитываем время ожидания обслуживания при различном числе кладовщиков (n=2,3,4,…). На основе таблицы затрат и потерь от простоя выясняем, что выгоднее содержать трех кладовщиков, т. к. затраты на их содержание будут больше, чем потери от простоя рабочих.
Литература
1. Баканов М.И., Шеремет А.Д. Теория экономического анализа: Учебник. – 4-е изд., доп. и перераб. – М.: Финансы и статистика, 1999
2. Браславец М.Е. Экономико – математические методы в организации и планировании сельскохозяйственного производства, 1974
3. Кравченко Р.Г., Попов И.Г., Толпекин С.З. Экономико – математические методы в организации и планировании сельскохозяйственного производства, 1974
4. Кузнецов Ю. Н., Кузубов В. И., Волощенко А. Б. Математическое программирование. Учебное пособие для ВУЗов. – М.: "Высшая школа", 1980.
|