План
лекції з навчальної дисципліни
Ф І З И К А
Тема: "ЕЛЕМЕНТИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ"
Вступ
Область застосовності класичного закону додавання швидкостей обмежена. Він, зокрема, непридатний для опису явищ, пов’язаних із розповсюдженням світла. Але, класичний закон додавання швидкостей являється наслідком із перетворень Галілея. Отже, і ці перетворення мають обмежену область застосовності.
Відмова від необгрунтованих застосовностей положень ньютонівської механіки дала можливість Ейнштейну розробити нову теорію – спеціальну теорію відносності, в основу якої покладені два принципи, які являються постулатами:
а) принцип відносності;
б) принцип інваріантності швидкості світла відносно інерційних систем відліку.
Ці постулати надійно підтверджені експериментально.
Границі застосовності класичної механіки. Спеціальна теорія відносності. Постулати Ейнштейна
Класична механіка, механіка Галілея-Ньютона, створена для опису руху макротіл із швидкостями в багато разів меншими швидкості світла. З перетворень Галілея-Ньютона випливає закон додавання швидкостей:
И=И´+V(1)
Де И – швидкість тіла в нерухомій системі,
И´ – швидкість його в рухомій системі,
V– швидкість руху системи.
В класичній механіці простір і час вважаються абсолютними і непов’язаними один з одним. Якщо існує абсолютний простір, то повинна існувати і абсолютна швидкість по відношенню до цього простору. В 1881 році американський вчений Майкельсон показав, що для швидкості світла відношення (1) не виконується. Абсолютної швидкості не існує. Фізики опинились у важкому становищі.
Вихід з цього становища вказав Ейнштейн. Він сформулював новий принцип відносності, більш загальний, ніж принцип Галілея і розробив спеціальну теорію відносності, яка базується на серйозному експериментальному фундаменті, і тому являє собою етап більш глибокого пізнання об’єктивних законів природи.
Теорія відносності описує рух тіл із швидкостями, близькими до швидкості світла. При малих швидкостях закони теорії відносності співпадають з законами класичної механіки. Таким чином, застосування законів класичної механіки обмежено. Вони застосовуються тільки для опису руху макротіл із швидкостями в багато разів меншими швидкості світла.
Закони класичної механіки не застосовуються для опису руху мікротіл. Рух мікротіл вивчається в квантовій механіці.
Згідно з уявленнями Ньютона простір і час є абсолютними і незалежними один від одного. Простір існує сам по собі, а час сам по собі.
Вчені вважали, що оскільки існує абсолютний простір, то повинна існувати і абсолютна система координат. Швидкість по відношенню до цієї системи є абсолютною. Вважали, що така система може бути пов’язана з світовим ефіром. Майкельсон в 1881 р. поставив дослід з метою визначення швидкості Землі відносно ефіру і одержав негативний результат. Таким чином, дослід показав, що абсолютної системи не існує. Результати досліду Майкельсона знайшли пояснення в теорії відносності Ейнштейна.
Спеціальна теорія відносності Ейнштейна будується на 2 постулатах:
1. Всі закони природи однакові (інваріантні по відношенню до переходу від однієї інерційної системи відліку до другої). Іншими словами, рівняння, що відбивають закони природи, інваріантні по відношенню до перетворень координат і часу при переході від однієї інерційної системи відліку до іншої.
2. Швидкість світла у вакуумі не залежить від швидкості руху джерела і однакова в усіх інерційних системах.
Перетворення Лоренца. Простір і час в спеціальній теорії відносності
Ейнштейн показав, що у відповідності з постулатами теорії відносності зв’язок між координатами і часом в двох інерційних системах відліку Sі S¢ (нерухомій і рухомій) здійснюється не перетвореннями Галілея, а перетвореннями Лоренца.
Перетворення
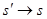
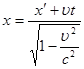 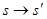  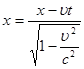
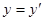 , , 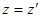 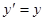 , , 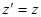 (2) (2)
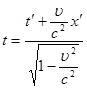 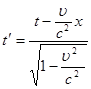
Використовуючи перетворення Лоренца, знайдемо довжину відрізка в обох системах координат:

 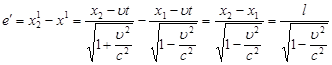 , тобто , тобто 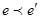 . .
Проміжок часу між двома подіями в обох системах буде рівний:

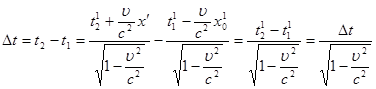 , тобто , тобто 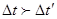 . .
В системі координат, відносно якої тіло рухається, тривалість події більша ніж в системі координат, відносно якої тіло рухається, а рухомий годинник іде повільніше, ніж годинник в системі s.
Закон додавання швидкостей:
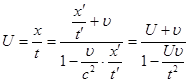 . .
Таким чином, з перетворень Лоренца випливає, що розміри тіл залежать від швидкості їхнього руху:
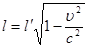 (3) (3)
Протікання процесів в системі, що рухається, затримується:
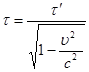 , , 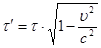 (4) (4)
Закон додавання швидкостей набуває вигляд:
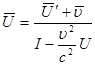 (5) (5)
Із перетворень Лоренца видно, що просторові координати пов’язані з часом. Отже, простір і час взаємозв’язані і утворюють єдине ціле – час. В теорії відносності простір-час розглядається як абсолютна форма існування матерії.
В теорії відносності розглядається 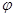 - вимірний світ простір-час. Незмінною величиною (інваріантом) в цьому світі є інтервал s, який визначається виразом: - вимірний світ простір-час. Незмінною величиною (інваріантом) в цьому світі є інтервал s, який визначається виразом:
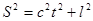 , (6), , (6),
де С – швидкість світла,
t – час, що пройшов від однієї події до іншої,
l– відстань між подіями.
Поняття про релятивістську динаміку. Класична механіка як частковий випадок релятивістської механіки
З принципу відносності (всі інерційні системи рівноправні) випливає, що математичний запис будь-якого закону фізики повинна бути однаковою в усіх інерційних системах відліку. Цю умову називають умовою інваріантності фізичних законів відносно перетворень Лоренцо.
Розглянемо основний закон класичної динаміки:
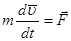 або або 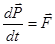 (7) (7)
Рівняння (7) інваріантне по відношенню до перетворень Галілея.
Дійсно, 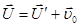 , але , але 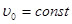 . .
Тому: 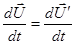 . .
Але рівняння (7) неінваріантне по відношенню до перетворень Лоренцо (при m=const).Згідно теорії відносності
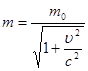 (8) (8)
З урахуванням (8) рівняння (7) залишається інваріантним по відношенню до перетворень Лоренца:
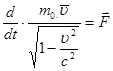 (9) (9)
Ейнштейн показав також, що маса і енергія взаємозв’язані співвідношенням 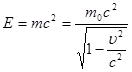
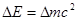 (10) (10)
Закон взаємозв’язку маси і енергії називають ще законом пропорційності маси і енергії. Він означає, що маса і енергія зростають або зменшуються одночасно. Якщо енергія тіла (частинка) змінюється на величину 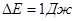 . то одночасно змінюється і його маса на . то одночасно змінюється і його маса на 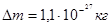 . Отже, не може бути мови про зведення маси до енергії (точка зору фізиків – ідеалістів). Можна стверджувати, що енергія і маса – властивості матерії, що рухається. . Отже, не може бути мови про зведення маси до енергії (точка зору фізиків – ідеалістів). Можна стверджувати, що енергія і маса – властивості матерії, що рухається.
Порівнюючи рівняння, ми бачимо, що при малих швидкостях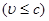
Перетворення Лоренцо переходить в перетворення Галілея. Це означає, що при цій умові закони класичної механіки правильно описують рух тіл. Отже, закони класичної механіки можна застосовувати тільки до тіл, що рухаються із швидкостями, що задовольняють умову 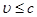 . .
Таким чином, теорія відносності містить в собі класичну механіку як частковий випадок. У розвиток теорії відносності великий внесок зробив російський вчений Френзель. Він збудував послідовну релятивістську теорію електрона, що має свій момент імпульсу. В.А. Рон дослідив декілька важливих задач теорії тяжіння. А.А. Фрідман заклав теорію загально релятивістської космології і ряд інших робіт.
Висновки
Уявлення про простір і час докорінно змінилися внаслідок розвитку електродинаміки і фізики великих швидкостей, яку називають релятивістською
фізикою.
Інтервал часу 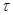 , виміряний у системі що рухається зі швидкістю , виміряний у системі що рухається зі швидкістю 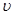 , дорівнює: , дорівнює: 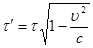 , де , де 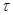 - інтервал часу в нерухомій системі. - інтервал часу в нерухомій системі.
Довжина стержня l в інерційній системі відліку, відносно якої він рухається зі швидкістю 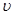 , дорівнює , дорівнює
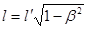 .
.
Довжина стержня найбільша в системі відліку, відносно якої він нерухомий.
Універсальний зв’язок між енергією і масою визначається:
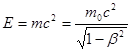 . .
Величину 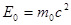 називають власною енергією
або енергією спокою тіла. називають власною енергією
або енергією спокою тіла.
План
лекції з навчальної дисципліни
Ф І З И К А
Тема: "ОСНОВНЕ РІВНЯННЯ ІДЕАЛЬНОГО ГАЗУ"
Вступ
Уявлення про те, що речовина складається з найдрібніших невидимих частинок, виникло в найдавніші часи на сході (у Фінікії, в Індії). Але тільки в стародавній Греції (в У-1У ст. до н.е.) атомізм виникає як матеріалістичне вчення, позбавлене релігійних уявлень.
Видатний російський вчений М.В. Ломоносов перший приклав цілком певне атомістичне уявлення до пояснення законів природи, зробивши атомістичну гіпотезу могутньою зброєю в руках природознавства. В наш час експериментально доведено, що всі матеріальні тіла складаються із великої кількості атомів чи молекул, які безперервно рухаються (хаотично) і взаємодіють між собою. Молекулярна фізика вивчає властивості і характеристики великої сукупності частинок, а не розглядає руху однієї частинки. Тому молекулярна фізика використовує статистичний метод і теорію ймовірності.
Молекулярно-кінетичний (статистичний) і термодинамічний методи вивчення макроскопічних систем
Молекулярною фізикою називається розділ фізики, в якому вивчають фізичні властивості тіл в залежності від їхньої будови, від сили взаємодії між молекулами, атомами, іонами, що утворюють тіла і від характеру руху цих частинок.
Задачею молекулярної фізики є встановлення зв’язку між фізичними величинами речовин і на основі створених нових речовин з наперед заданими властивостями.
Молекулярна фізика не цікавиться поведінкою однієї окремої молекули. Вона вивчає властивості великої сукупності частинок. Тому основним методом молекулярної фізики є статистичний метод, а фізичні закономірності, що встановлюються молекулярною фізикою, мають імовірнісний, статистичний характер. В основі молекулярної фізики лежать фундаментальні положення:
1. Всі тіла складаються з найдрібніших частинок – атомів. В деяких тілах при певних умовах атоми з’єднуються в молекули.
1. Атоми і молекули взаємодіють між собою. Величина сил взаємодії залежить від відстані між частинками. У твердих тіл взаємодія складніша, ніж в рідинах та газах.
2. Молекули та атоми знаходяться в стані неперервного хаотичного руху. Цей хаотичний рух ми сприймаємо як теплоту. Чим більше кінетична енергія молекулярного руху, тим вища температура і навпаки. Звідси випливає, що тіло можна нагріти і без вогню.
Щоб нагріти тіло, достатньо виконати над ним роботу. Так наковальня нагрівається при ударах, газ нагрівається при стисканні.
Вперше ці положення розвинув російський вчений М. В Ломоносов. Ще задовго до нашої ери виникло вчення про найменші частинки з яких складається будь-яка речовина. Але вперше широкий розвиток атомна гіпотеза одержала в працях Ломоносова /1711–1765 рр./, який зробив спробу дати єдину картину всіх відомих в його час фізичних і хімічних явищ. При цьому він виходив з корпускулярного /молекулярного/ уявлення про будову матерії. Виступаючи проти пануючої в його час теорії тепловоду /гіпотези теплової рідини, місткість якої в тілі визначає ступінь його нагрітості/. М.В. Ломоносов «причину тепла» бачив у обертовому русі частинок тіла. Таким чином, Ломоносов вперше сформулював молекулярно-кінетичні уявлення.
Фізична модель та рівняння стану ідеального газу
Для опису властивостей реальних газів необхідно враховувати розміри молекул і сили взаємодії між ними. Але при невеликих тисках і дуже низьких температурах розмірами молекули і їх взаємодією можна знехтувати.
Такий газ, молекули якого можна вважати матеріальними точками, які не взаємодіють між собою, називається ідеальним газом.
Стан газу характеризується трьома величинами – об’ємом V, тиском P і температурою T. Ці величини називаються параметрами газу. Всі параметри даної маси газу пов’язані між собою з допомогою рівняння стану газу.
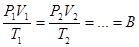 , (1) , (1)
де B –
деяка константа.
Ця константа для 1 моля позначається буквою R і називається універсальною газовою сталою. Чисельне значення сталої R знайдемо, підставивши в рівняння стану значення параметрів газу в нормальних умовах:
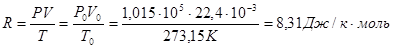
Отже для 1 моля маємо таке рівняння:
PV=RT (2)
Для будь-якої маси газу m рівняння стану запишеться так:
PV=(m/m) RT (3)
Це рівняння називається рівнянням Клайперона-Мендєлєєва. В формулі /3/ (m
/
m
)
являє собою число молей даної маси газу.
Відмітимо, що для того, щоб рівняння /2/ описувало властивості реального газу, в нього потрібно ввести поправки на об’єм В який займали б молекули газу при щільному упакуванні і на силу притягання між молекулами a
/
V
2
. Тоді одержимо таке рівняння:
(
P
-
a
/
V
2
) (
V
-
B
) =
RT
(4)
Рівняння /4/ називають рівнянням Ван-дер-Ваальса. Сталі а і в називають поправними Ван-дер-Ваальса. З формули /4/ випливає, що при р®¥:
V-b®0, тобто V®b
Отже, при збільшенні тиску об’єм газу прямує до власного об’єму молекул газу, а не до нуля, формула /4/ є набагато кращим наближенням до дійсності, ніж /2/. Але і вона не абсолютно точна.
Основне рівняння молекулярно-кінетичної теорії газу. Середня кінетична енергія молекул газу
З курсу фізики середньої школи відомо, що властивості ідеальних газів описуються рівняннями Бройля-Маріота, Гей-Люсака, та ін., знайденими експериментально. Але можна, теоретично вивести рівняння, з якого всі зазначені вище закони будуть випливати як наслідки. Тому таке рівняння називають основним рівнянням кінетичної теорії газів.
Основним рівнянням кінетичної теорії газів називають рівняння, що встановлює зв’язок між тиском газу і його енергією. При своєму рухові молекули газу неперервно ударяється об стінки посудини. Удари чергуються один за одним дуже швидко, усереднюються і створюють постійну силу, що діє на стінки посудини. Внаслідок цього газ створює на стінки посудини тиск, який дорівнює:
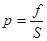 , (5) , (5)
де f
– сила, що діє на стінку, S
– площа стінки.
Знайдемо цей тиск. Для цього розглянемо посудину з газом у вигляді кубу з довжиною ребра l
(рис. 1) в якому хаотично рухаються молекули.
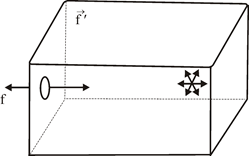
Рис. 1
В зв’язку з повною хаотичністю руху молекул можна вважати, що  всіх молекул рухаються прямолінійно між передньою і задньою стінками куба, всіх молекул рухаються прямолінійно між передньою і задньою стінками куба,  молекул – між правою і лівою стінками і молекул – між правою і лівою стінками і  – між верхньою і нижньою гранями. Від такого спрощення результат дії молекул не змінюється. – між верхньою і нижньою гранями. Від такого спрощення результат дії молекул не змінюється.
При пружному ударі об стінку, маса якої нескінченно велика в порівнянні з масою молекули m
,
кожна молекула, що рухається зі швидкістю n
, в результаті чого її імпульс зміниться на величину, рівну:
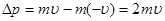 . .
Ця зміна імпульсу молекули відбувається під дією імпульсу сили 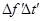 , що діє зі сторони стінки на молекулу під час удару. За другим законом Ньютона маємо: , що діє зі сторони стінки на молекулу під час удару. За другим законом Ньютона маємо:
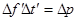 , ,
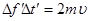 , (6) , (6)
де 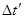 – тривалість удару. – тривалість удару.
По третьому закону Ньютона сила, чисельно рівна 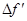 , буде діяти зі сторони молекули на стінку. Відскочивши від стінки, молекула полетить до протилежної стінки, і, відскочивши від неї, знову вернеться до першої стінки через деякий час D
t
. Середня сила D
f
, що діє на стінку за весь час між двома послідовними ударами молекули, визначиться з умови, що її імпульс , буде діяти зі сторони молекули на стінку. Відскочивши від стінки, молекула полетить до протилежної стінки, і, відскочивши від неї, знову вернеться до першої стінки через деякий час D
t
. Середня сила D
f
, що діє на стінку за весь час між двома послідовними ударами молекули, визначиться з умови, що її імпульс 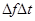 повинний чисельно дорівнювати імпульсу сили повинний чисельно дорівнювати імпульсу сили 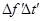 , що діє в продовж , що діє в продовж 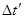 . Тоді замість рівняння (6) маємо: . Тоді замість рівняння (6) маємо:
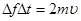 (7) (7)
Величина D
t
являє собою час, за який молекула проходить відстань 2
l
.
Отже:
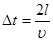 (8) (8)
Підставляючи це значення 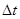 в формулу (7), одержимо: в формулу (7), одержимо:
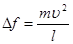 (9) (9)
Ми знайшли середню силу удару однієї молекули. Але різні молекули рухаються з різними швидкостями 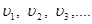 Тоді сумарна сила удару молекул об стінку буде рівна: Тоді сумарна сила удару молекул об стінку буде рівна:
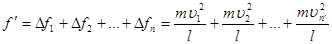 (10) (10)
де 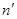 – число молекул, що рухаються між двома протилежними стінками. – число молекул, що рухаються між двома протилежними стінками.
В першій частині рівняння (10) винесемо 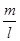 за дужки, помножимо і поділимо його на за дужки, помножимо і поділимо його на 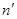 . Одержимо: . Одержимо:
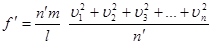 (11) (11)
Величина 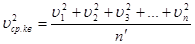 являє собою середнє значення квадратів швидкостей молекул, а величина, рівна являє собою середнє значення квадратів швидкостей молекул, а величина, рівна 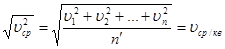 називається середньою квадратичною швидкістю. Тоді замість (11) маємо: називається середньою квадратичною швидкістю. Тоді замість (11) маємо:
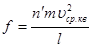 (12) (12)
Як вказано вище, число молекул, що рухаються між двома протилежними стінками, 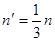 . Отже, одержуємо: . Отже, одержуємо:
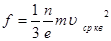 (13) (13)
Підставивши це значення f
в формулу (5) і враховуючи, що площа грані 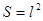 знаходимо: знаходимо:
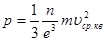 . (14) . (14)
Але 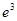 – об’єм кубу. Отже – об’єм кубу. Отже 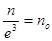 – являє собою число молекул в одиниці об’єму. Тому маємо: – являє собою число молекул в одиниці об’єму. Тому маємо:
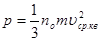 . (15) . (15)
З останнього виразу випливає, що тиск, що виконує газ на стінки посудини визначається числом молекул в одиниці об’єму 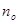 , масою молекули m
і середньою квадратичною швидкістю. , масою молекули m
і середньою квадратичною швидкістю.
Формулу (10) можна записати в іншому вигляді. Помноживши і поділивши праву частину на два, одержимо:
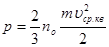 , (16) , (16)
але 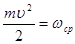 – представляє собою середню кінетичну енергію руху молекули. Тому маємо: – представляє собою середню кінетичну енергію руху молекули. Тому маємо:
 . (17) . (17)
тобто тиск газу пропорційний середній кінетичній енергії молекул одиниці об’єму.
Співвідношення (15) і еквіваленти (17) називається основним рівнянням кінетичної теорії газів згідно (17) тиск газу дорівнює 2/3 кінетичної енергії поступального руху молекул, вміщених в одиниці об’єму.
Таким чином, для обрахунків тиску газу необхідно знати середню кінетичну енергію молекул або їхню середню квадратичну швидкість. Найчастіше відома температура газу. Тому знайдемо формулу для визначення цих величин через температуру газу. Для цього помножимо ліву і праву частини рівняння (17) на об’єм одного моля Vo
, одержимо:
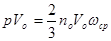 (10) (10)
Але по 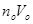 – кількість молекул в 1 молі. Отже – кількість молекул в 1 молі. Отже 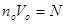 – число Авогадро. – число Авогадро.
Тому формула (18) має вигляд:
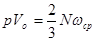 (19) (19)
Порівнюючи вираз (19) з рівнянням стану ідеального газу 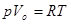 , знаходимо: , знаходимо:
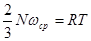 (20) (20)
Звідси
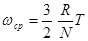 (21) (21)
Оскільки R
і
N
– величини сталі, то і величина k
рівна:
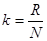 (22) (22)
теж буде сталою. Вона носить назву сталої Больцмана. Її значення дорівнює:
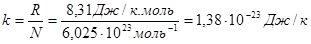
Після чого формула (21) записується так:
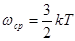 (23) (23)
Стала Больцмана k
є однією з найважливіших фундаментальних фізичних сталих і має зміст універсальної газової сталої, віднесеної до однієї молекули газу.
З рівняння (23) випливає молекулярно-кінетичний зміст температури. Температура газу визначається середньою кінетичною енергією поступального руху молекул.
Вираз (23) можна записати так:
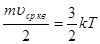 (24) (24)
Звідси можна визначити середню квадратичну швидкість молекул:
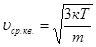 (25) (25)
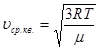 (26) (26)
Підставивши в формулу (17) значення середньої кінетичної енергії за формулою (23):
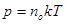 (27) (27)
Рівняння (27) дозволяє обчислити кількість молекул, наприклад, в електровакуумних приладах.
Розподіл молекул газів по швидкостях при тепловій рівновазі (розподіл Максвелла)
Як же розподіляються молекули газів в залежності від їхніх швидкостей тобто, скільки молекул рухається швидко і скільки повільно? Цю задачу вперше розв’язав Максвелл. Він знайшов рівняння, за допомогою якого можна визначити, скільки молекул має швидкість, близьку до даної швидкості 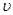 . Іншими словами, рівняння Максвелла дозволяє визначити кількість молекул, що мають швидкість в інтервалі (n
,
n
+
D
n
). . Іншими словами, рівняння Максвелла дозволяє визначити кількість молекул, що мають швидкість в інтервалі (n
,
n
+
D
n
).
Визначимо спочатку, від чого повинна залежати кількість частинок D
n
, швидкості яких лежать в інтервалі (n
,
n
+
D
n
). Наприклад в інтервалі 100, 101 м/с або 367, 370 м/с і т.д. Очевидно, найбільша кількість частинок має швидкості, близькі до середньої швидкості, а кількість частинок з дуже малими швидкостями, як і кількість з дуже великими швидкостями, мала. Отже, кількість частинокD
n
, що приходиться на однакові інтервали швидкостей D
n
залежить від розглядуваної швидкості n
. Іншими словами, так звана функція розподілу Максвелла повинна бути функцією швидкостей f
(
n
)
, тобто: 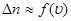
Фізично також ясно, що число 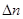 буде пропорційне ширині інтервала швидкостей D
n
і кількості молекул в одиниці об’єму n
. Тому можемо записати таке співвідношення: буде пропорційне ширині інтервала швидкостей D
n
і кількості молекул в одиниці об’єму n
. Тому можемо записати таке співвідношення:
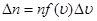 (28) (28)
Або, переходячи до нескінченно малих величин 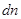 і і 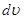 , одержуємо: , одержуємо:
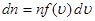 (29) (29)
Звідки знаходимо:
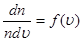 (30) (30)
Функцію f
(
n
)
називають функцією розподілу. Її фізичний зміст випливає з (30). Дійсно при D
n
= 1 м/
c
маємо: 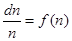 , тобто, f
(
n
)
рівна долі частинок, швидкості яких лежать в одиничному інтервалі швидкостей поблизу даної швидкостіn. , тобто, f
(
n
)
рівна долі частинок, швидкості яких лежать в одиничному інтервалі швидкостей поблизу даної швидкостіn.
На основі теорії ймовірностей Максвелл знайшов вигляд цієї функції:
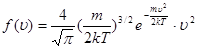 . .
На рис. 2 приведений графік функції f
(
n
)
. З графіка видно, що f
(
n
)
функція має максимум при певному значенні швидкості 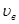 . Це значить, що найбільшу кількість молекул в газі мають швидкості, близькі до . Це значить, що найбільшу кількість молекул в газі мають швидкості, близькі до 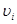 . Тому швидкість . Тому швидкість 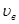 називають найбільш ймовірною. називають найбільш ймовірною.
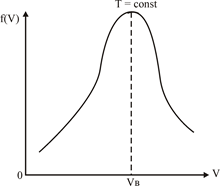
Рис. 2
Найбільш ймовірна швидкість рівна:
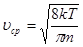 (31) (31)
Враховуючи значення найбільш ймовірної швидкості формулу (31) можна записати в такому вигляді:
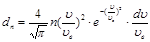 (32) (32)
Формула Максвелла дозволяє обчислити і середню арифметичну швидкість. Вона рівна:
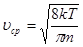 або або 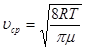 (33) (33)
Тепер можна знайти формули для визначення кількості молекул dn
, швидкості яких лежать в інтервалі (n
,
n
+
d
n
). Так, підставивши значення f
(
n
)
по формулі (33) в формулу (30) одержимо:
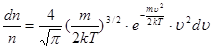 (34) (34)
Таким чином, властивості газу визначаються такими швидкостями:
Середня квадратична – 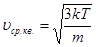
Середня арифметична –
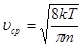
Найбільш ймовірна –
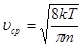
Звідси видно, що 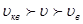 (рис. 3). (рис. 3).
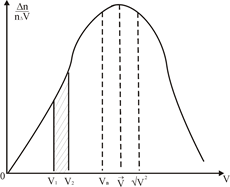
Рис. 3
Фізичний зміст цих швидкостей полягає в наступному. За допомогою графіку (рис. 3) можна знайти кількість молекул, швидкості яких лежать між 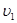 і і 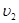 . Для цього перемножимо середнє значення ординати цього інтервалу на ширину інтервалу. Тоді одержимо: . Для цього перемножимо середнє значення ординати цього інтервалу на ширину інтервалу. Тоді одержимо:
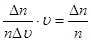 . .
Ми знайшли відносну кількість молекул, швидкості яких лежать в інтервалі (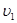 , , 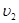 ), але цей добуток дорівнює площі фігури, закресленої на рис. 3. Таким чином, маючи графік розподілу Максвелла для якогось газу можна легко визначити відносну кількість молекул, швидкості яких лежать в даному інтервалі. ), але цей добуток дорівнює площі фігури, закресленої на рис. 3. Таким чином, маючи графік розподілу Максвелла для якогось газу можна легко визначити відносну кількість молекул, швидкості яких лежать в даному інтервалі.
Функція розподілу Максвелла залежить від температури (рис. 4).
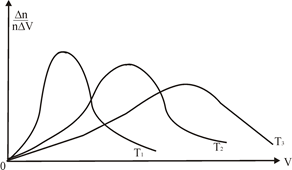
Рис. 4
Як видно з рис. 4 при 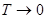 максимум функції обертається в гострий пік. максимум функції обертається в гострий пік.
Отже діапазон швидкостей навколо 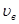 при зменшенні температури зменшується. При підвищенні температури все більше зменшується кількість молекул, швидкості яких менше найбільш ймовірної і збільшується частина молекул, швидкості яких перевищують найбільш ймовірну.
при зменшенні температури зменшується. При підвищенні температури все більше зменшується кількість молекул, швидкості яких менше найбільш ймовірної і збільшується частина молекул, швидкості яких перевищують найбільш ймовірну.
Висновки
1. Молекулярна фізика розглядає будь-яке тіло як таке, що складається з надзвичайно великої кількості частинок – атомів чи молекул і характеризує таку велику сукупність середніми величинами на основі методів статистичної фізики.
2. Основним рівнянням ідеального газу, яке враховує можливу зміну всіх параметрів газу, є рівняння Менделєєва-Клапейрона, або рівняння стану ідеального газу.
3. Тиск газу пропорційний середній кінетичній енергії молекул одиниці об’єму, або тиск газу пропорційний абсолютній температурі газу, а температура газу є мірою середньої кінетичної енергії поступального руху молекул.
4. Розподіл Максвелла дає змогу визначити частки молекул, швидкості яких розміщені в інтервалі від n
доn
+
d
n
. Розподіл дає змогу знайти швидкості молекул: середню, середню квадратичну, найбільш ймовірну.
|