|
Магазин торгует подержанными автомобилями. Статистика их потребительских цен накапливается в базе данных. В магазин пригоняют на продажу очередную партию небольших однотипных автомобилей. Как назначить их цену? Статистический подход позволяет дать прогноз среднего значения цены и доверительных интервалов для него.
Цена автомобиля зависит от множества факторов. К числу объясняющих переменных можно отнести, например, модель автомобиля, фирму-производитель, регион производства (Европа, США, Япония), объем двигателя, фирму-производитель, регион производства (Европа, США, Япония), объем производителя, количество цилиндров, время разгона до 100 км/час, пробег, потребление горючего, год выпуска и т.д. Первые из названных переменных очень важны при ценообразовании, но они – качественные. Традиционный регрессионный анализ, рассматриваемый в этом задании, предназначен для количественных данных. Поэтому, не претендуя на высокую точность, не будем включать их в эконометрическую модель. Сделаем выборку, например, только для автомобилей одной фирмы-производителя. Пусть, например, оказалось, что продано n= 16 таких автомобилей. Для упрощения выберем из базы данных цены yi
(i = 1......16) проданных автомобилей и только две объясняющие переменные: возраст хi
1
(i = 1, …..16) в годах и мощность двигателя хi
2
(i = 1, ….16) в лошадиных силах. Выборка представлена в таблице:
| I номер |
yi
, цена, тыс. у.е. |
хi1
возраст,лет |
хi2
, мощность двигателя |
| 1
|
11 |
5,0 |
155 |
| 2 |
6 |
7,0 |
87 |
| 3 |
9,8 |
5,0 |
106 |
| 4 |
11 |
4,0 |
89 |
| 5 |
12,3 |
4,0 |
133 |
| 6 |
8,7 |
6,0 |
94 |
| 7 |
9,3 |
5,0 |
124 |
| 8 |
10,6 |
5,0 |
105 |
| 9 |
11,8 |
4,0 |
120 |
| 10 |
10,6 |
4,0 |
107 |
| 11 |
5,2 |
7,0 |
53 |
| 12 |
8,2 |
5,0 |
80 |
| 13 |
6,5 |
6,0 |
67 |
| 14 |
5,7 |
7,0 |
73 |
| 15 |
7,9 |
6,0 |
100 |
| 16 |
10,5 |
4,0 |
118 |
1. Построить поля рассеяния между ценой y и возрастом автомобиля х1
, между ценой y и мощностью автомобиля x2
. На основе их визуального анализа выдвинуть гипотезу о виде статистической зависимости y от х1
и y от х2
. Найти точечные оценки независимых параметров
а0
а1
модели y = а0
+ а1
х1
+ ε и
β1
β2
модели y = β0
+ а1
х1
+ δ
2. Проанализировать тесноту линейной связи между ценой и возрастом автомобиля, а также ценой и мощностью двигателя х2
. Для этого рассчитать коэффициенты парной корреляции ryx
1
и ryx
2
и проверить их отличие от нуля при уровне значимости α = 0,1.
3. Проверить качество оценивания моделей на основе коэффициента детерминации, F- и t- критериев при уровне значимости α = 0,05 и α = 0,10.
4. Проверить полученные результаты с помощью средств MicrocoftExcel.
5. С помощью уравнений регрессии рассчитать доверительные интервалы для среднего значения цены, соответствующие доверительной вероятности 0,9. Изобразить графически поля рассеяния, линии регрессии и доверительные полосы.
На продажу поступила очередная партия однотипных автомобилей. Их возраст х1
равен 3 года. Мощность двигателя х2
= 165 л.с. Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей по моделям y = а0
+ а1
х1
+ ε и y = β0
+ а1
х1
+ δ с доверительной вероятностью 0,9.
Решение:
На основе поля рассеяния, построенного на основе табл. 1, выдвигаем гипотезу о том, что зависимость цены y от возрастаавтомобиля x1
описывается линейной моделью вида
y = а0
+ а1
х1
+ ε
где а0
и а1
– неизвестные постоянные коэффициенты, а ε – случайная переменная (случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерений.
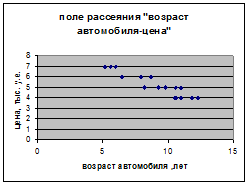
Рисунок 1 – Поле рассеяния «возраст автомобиля-цена»
Аналогично, на основе анализа поля рассеяния (рис. 2), также построенного на основе таблицы 1, выдвигаем гипотезу о том, что зависимость цены y от мощности автомобиля x2
описывается линейной моделью вида
y = β0
+ β1
х1
+ δ
где β0
и β1
– неизвестные постоянные коэффициенты, а ε – случайная переменная (случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерений.
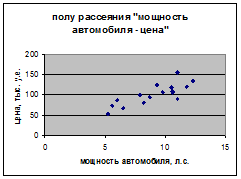
Рисунок 2 – Поле рассеяния «мощность автомобиля-цена»
На основе табл. 1 исходных данных для вычисления оценок параметров моделей составляется вспомогательная табл. 1.1. Воспользуемся формулами и левой частью таблицы 1.1. для нахождения оценок а0
и а1
.
Так как n = 16, получаем
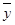 = 145/16=9.0625 = 145/16=9.0625
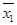 = 84.0/16=5.25 = 84.0/16=5.25
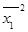 = 27.5625 = 27.5625
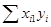 = 365 = 365
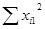 = 460 = 460
| i |
yi
|
xi1
|
xi1
2
|
xi1
yi
|
yi
2
|
i |
yi
|
xi2
|
xi2
2
|
xi2
yi
|
| 1
|
11 |
5.0 |
25 |
55 |
121 |
1 |
11 |
155 |
24025 |
1705 |
| 2 |
6 |
7.0 |
49 |
42 |
36 |
2 |
6 |
87 |
7569 |
522 |
| 3 |
9,8 |
5.0 |
25 |
49 |
96,04 |
3 |
9,8 |
106 |
11236 |
1038,8 |
| 4 |
11 |
4.0 |
16 |
44 |
121 |
4 |
11 |
89 |
7921 |
979 |
| 5 |
12,3 |
4.0 |
16 |
49,2 |
151,29 |
5 |
12,3 |
133 |
17689 |
1635,9 |
| 6 |
8,7 |
6.0 |
36 |
52,2 |
75,69 |
6 |
8,7 |
94 |
8836 |
817,8 |
| 7 |
9,3 |
5.0 |
25 |
46,5 |
86,49 |
7 |
9,3 |
124 |
15376 |
1153,2 |
| 8 |
10,6 |
5.0 |
25 |
53 |
112,36 |
8 |
10,6 |
105 |
11025 |
1113 |
| 9 |
11,8 |
4.0 |
16 |
47,2 |
139,24 |
9 |
11,8 |
120 |
14400 |
1416 |
| 10 |
10,6 |
4.0 |
16 |
42,4 |
112,36 |
10 |
10,6 |
107 |
11449 |
1134,2 |
| 11 |
5,2 |
7.0 |
49 |
36,4 |
27,04 |
11 |
5,2 |
53 |
2809 |
275,6 |
| 12 |
8,2 |
5.0 |
25 |
41 |
67,24 |
12 |
8,2 |
80 |
1600 |
656 |
| 13 |
6,5 |
6.0 |
36 |
39 |
42,25 |
13 |
6,5 |
67 |
4489 |
435,5 |
| 14 |
5,7 |
7.0 |
49 |
39,9 |
32,49 |
14 |
5,7 |
73 |
5329 |
416,1 |
| 15 |
7,9 |
6.0 |
36 |
47,4 |
62,41 |
15 |
7,9 |
100 |
10000 |
790 |
| 16 |
10,5 |
4.0 |
16 |
42 |
110,25 |
16 |
10,5 |
118 |
13924 |
1239 |
| Сумма |
145,1 |
84.0 |
460 |
726,2 |
1393,15 |
145,1 |
1611 |
167677 |
15327,1 |
Следовательно,
а1
= 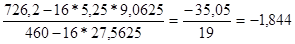
а0
= 9,0625- (-1,844) * 5.25 = 18,74
Таким образом,
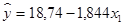
Аналогично находятся оценки коэффициентов второй регрессионной модели y = β0
+ β1
х1
+ δ. При этом используется правая часть таблицы
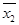 = 1611/16=100,6875 = 1611/16=100,6875
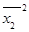 = 10137.97 = 10137.97
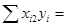 = 153271,1 = 153271,1
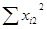 = 167677 = 167677
β1
= 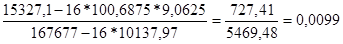
β 0
= 9,0625- 0,0099 * 100.6875= 2.0355
Окончательно получаем:
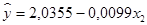
Подставляем соответствующие значения в формулу:
ryx
= 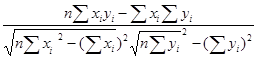
ryx
1
= 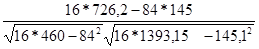 = 0,915 = 0,915
ryx
2
= 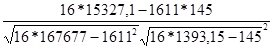 = 0.8 = 0.8
В нашей задаче t0.95;14
= 1,761
Для ryx
1
получаем
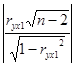 = = 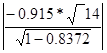 = 0,955 <1.761 = 0,955 <1.761
Условие не выполняется, следовательно, коэффициент парной корреляции не значим, гипотеза отвергается, между переменными отсутствует линейная связь
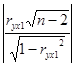 = = 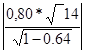 = 4.98>1.761 = 4.98>1.761
Условие выполняется, следовательно, коэффициент парной корреляции значимый, гипотеза подтверждается, между переменными существует сильная линейная связь
Коэффициент парной корреляции ryx
связан с коэффициентом а1
уравнения регрессии
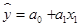 следующим образом следующим образом
ryx
= a1
Sx
/Sy
где Sx
, Sy
– выборочные среднеквадратичные отклонения случайных переменных х и y соответственно, рассчитывающиеся по формулам:
Sx1
= √ Sx1
2
Sx1
2
= 1/n ∑(xi
- 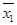 )2 )2
Sy
= √ Sy
2
Sy
2
= 1/n ∑(yi
- 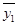 )2 )2
ryx
1
= 0,915
ryx
2
= 0,8
R2
= ryx
1
2
= 0,8372
Вариация на 83,72 % объясняется вариацией возраста автомобиля
R2
= ryx
2
2
= 0,64
Вариация на 64 % объясняется вариацией мощности двигателя автомобиля
Рассчитаем фактическое значение F- статистики Фишера по формуле:
F=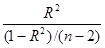
F=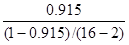 = 0,768 для зависимости y от х1 = 0,768 для зависимости y от х1
F=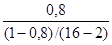 = 0,285для зависимости y от х2 = 0,285для зависимости y от х2
Fт
= 4,6
Поэтому для зависимостей y от х1
и y от х2
выполняется неравенство
Fт
<Fф
гипотеза отклоняется и признается статистическая значимость уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии используется t-критерий Стьюдента.
Для зависимости y от х1
:
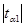 = √F = √0,768 = 0,876 = √F = √0,768 = 0,876
Поскольку это значение меньше 1,761, то принимаем нулевую гипотезу равенства нулю а1
Для зависимости
y от х2
:
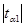 = √F = √0,285 = 0,533 = √F = √0,285 = 0,533
Поскольку это значение меньше 1,761, то принимаем нулевую гипотезу равенства нулю а1
Проверка с помощью MicrosoftExcel
| Оценка параметра а1 |
-1,87237 |
Оценка параметра а0 |
18,89868 |
| Среднеквадратическое отклонение |
0,200234 |
Среднеквадратическое отклонение а0 |
1,073633 |
| Коэффициент детерминации R2
|
0,861987 |
Среднеквадратическое отклонение y |
0,872798 |
| F-Статистика |
87,43972 |
Число степеней свободы |
14 |
| Регрессионная сумма квадратов |
66,60951 |
Остаточная сумма квадратов |
10,66487 |
| Оценка параметра а1 |
0,0698523 |
Оценка параметра а0 |
2,0354973 |
| Среднеквадратическое отклонение |
0,013746 |
Среднеквадратическое отклонение а0 |
1,4271948 |
| Коэффициент детерминации R2
|
0,648444 |
Среднеквадратическое отклонение y |
1,3929996 |
| F-Статистика |
25,822959 |
Число степеней свободы |
14 |
| Регрессионная сумма квадратов |
50,108105 |
Остаточная сумма квадратов |
27,16627 |
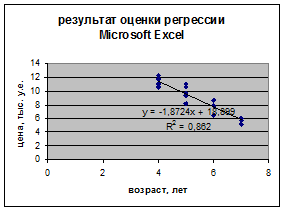
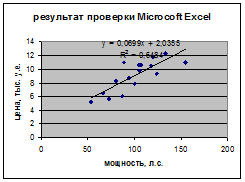
Рассчитаемдоверительный интервал среднего значения цены для y = a0
+ a1
x1
/
: ŷв.н. = ŷ(х0
) ± t1-
α
/2,
n
-2
Sŷ
,
где ув
, ун
– соответственно верхняя и нижняя границы
доверительногоинтервала;
ŷ(х0
) – точечный прогноз;
t1-
α
/2,
n
-2
–квантиль распределения Стьюдента;
(1-α/2) – доверительная верояность;
(n-2) – число степеней свободы;
: ŷв.н. = ŷ(х0
) ± t1-
α
/2,
n
-2
Sŷ
,
ta
= 2,57
Доверительный интервал для уn
:
Нижняя граница интервала:
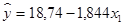 = 18,74-1,844*5 = 9,52 = 18,74-1,844*5 = 9,52
Верхняя граница интервала:
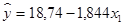 = 18,74-1,844*7 = 5,832 = 18,74-1,844*7 = 5,832
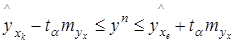
Sx1
2
= 1/n ∑(xi
- 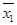 )2
= 19/16 = 1,1875 )2
= 19/16 = 1,1875
Sx1
= 1,089
| xi1
|
xi1
-
хср1
|
(xi1
-
хср1)
2
|
х2
|
х1
х2
|
| 5.0 |
-0,25 |
0,0625 |
155 |
775 |
| 7.0 |
1,75 |
3,0625 |
87 |
609 |
| 5.0 |
-0,25 |
0,0625 |
106 |
530 |
| 4.0 |
-1,25 |
1,5625 |
89 |
356 |
| 4.0 |
-1,25 |
1,5625 |
133 |
532 |
| 6.0 |
0,75 |
0,5625 |
94 |
564 |
| 5.0 |
-0,25 |
0,0625 |
124 |
620 |
| 5.0 |
-0,25 |
0,0625 |
105 |
525 |
| 4.0 |
-1,25 |
1,5625 |
120 |
480 |
| 4.0 |
-1,25 |
1,5625 |
107 |
428 |
| 7.0 |
1,75 |
3,0625 |
53 |
371 |
| 5.0 |
-0,25 |
0,0625 |
80 |
400 |
| 6.0 |
0,75 |
0,5625 |
67 |
402 |
| 7.0 |
1,75 |
3,0625 |
73 |
511 |
| 6.0 |
0,75 |
0,5625 |
100 |
600 |
| 4.0 |
-1,25 |
1,5625 |
118 |
472 |
| 19 |
8175 |
myx
= S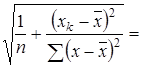 1,089*√1/16 + 1,5625/19 = 0,414 1,089*√1/16 + 1,5625/19 = 0,414
5,832 – 2,57*0,414 ≤ yn
≤ 5,832 + 2,57*0,414
На продажу поступила очередная партия однотипных автомобилей. Их возраст xp
1
= 3 года. Мощность двигателя xp
2
= 165 л.с.
Рассчитаем точечный и интервальный прогноз среднего значения цены поступивших автомобилей по первой парной регрессионной модели
y = β0
+ β1
х1
+ δ
Подставляем xp
1
в уравнение регрессии: 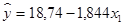
Получим точечный интервальный прогноз среднего цены.
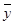 (xp
1
) = 18,74 – 1,844*3 = 13,208 тыс. у.е. (xp
1
) = 18,74 – 1,844*3 = 13,208 тыс. у.е.
Подставляем точечный интервальный прогноз среднего цены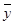 (xp
1
) = 12,3 тыс. и xp
1
= 3 года в уравнения границ доверительного интервала регрессии. Получим интервальный прогноз с доверительной вероятностью 0,9 (xp
1
) = 12,3 тыс. и xp
1
= 3 года в уравнения границ доверительного интервала регрессии. Получим интервальный прогноз с доверительной вероятностью 0,9
ŷв.н. = 13,208±2,57*0,414 или ŷн = 12,14 тыс. у.е.,
ŷв = 14,27 тыс. у.е.
Найти по методу наименьших квадратов оценки коэффициентов множественной регрессионной модели
y = а0
+ а1
х1
+ а2
х2
+ε
Проверить качество оценивания моделей на основе коэффициента детерминации и F-критерия. Пояснить их содержательный смысл.
Проверить полученные в заданиях результаты с помощью средств MicrocoftExcel.
Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей по множественной модели y = а0
+ а1
х1
+ а2
х2
+ε с доверительной вероятностью 0,9. Как в задаче 1, возраст поступивших автомобилей х1
= 3 года, мощность двигателя х2
= 165 л.с.
На основе полученных в задачах 1-2 статистических характеристик провести содержательную интерпретацию зависимости цены автомобиля от возраста и мощности двигателя.
Сумма произведений ∑х1
х2
равна: 8175
ХТ
Х = 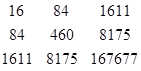 ХТ
Y = ХТ
Y =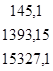
Найдем матрицу (Хт
Х), обратную матрице ХТ
Х.
Для этого сначала вычислим определитель.
ХТ
Х = 16*460*167667+1611*84*8175+1611*84*8175-1611*460*1611-84*84*167677-16*8175*8175 = 1234102720+1106273700+1106273700-1193847660-1183128912-1069290000 = 383548
Определим матрицу алгебраических дополнений
В таблице представлены ежегодные данные объема продаж автомагазина. Построить график во времени. Выдвинуть гипотезу о наличии тренда. Оценить неизвестные параметры линейной трендовой модели z = а0
а1
t +ε с методом наименьших квадратов.
Таблица 2 Ежегодные объемы продаж
| t годы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| zt
, продажи, тыс.у.е. |
350 |
314 |
300 |
293 |
368 |
393 |
339 |
443 |
467 |
457 |
488 |
424 |
Для найденного уравнения тренда построить доверительную полосу при уровне доверия 0,9. Изобразить графически точечный и интервальный прогноз среднего объема продаж.
В таблице 3 объемы продаж zt
в тыс. у.е. детализированы по месяцам. Построить график объема продаж во времени. Выдвинуть гипотезу о наличии линейного тренда и сезонных колебаний объема продаж:
z1 =
а0
а1
t + а2
cos (2πt/12) + а3
sin (2πt/12) + εt
Оценить параметры этой модели методом наименьших квадратов.
По уравнению трендово-сезонной модели найти точечный прогноз среднего объема продаж на 12 месяцев и интервальный прогноз среднего объема продаж на 1 месяц вперед при доверительной вероятности 0,9.
Ежемесячные объемы продаж
| t,годы |
Zt
|
t |
yt
t |
t2
|
| 1 |
2 |
3 |
4 |
5 |
| 1 |
350 |
1 |
350 |
1 |
| 2 |
314 |
2 |
728 |
4 |
| 3 |
300 |
3 |
900 |
9 |
| 4 |
293 |
4 |
1172 |
16 |
| 5 |
368 |
5 |
1840 |
25 |
| 6 |
393 |
6 |
2358 |
36 |
| 7 |
339 |
7 |
2373 |
49 |
| 8 |
443 |
8 |
3544 |
64 |
| 9 |
467 |
9 |
3736 |
81 |
| 10 |
457 |
10 |
4570 |
100 |
| 11 |
488 |
11 |
5368 |
121 |
| 12 |
424 |
12 |
5088 |
144 |
| 78 |
4636 |
78 |
32027 |
650 |
∑t = ½*12 (12+1) = 78
∑t2
= 1/6 *12 (12+1) (24+1)= 650
а0
= 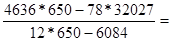 515294/1716=283,61 515294/1716=283,61
а1
=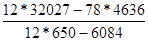 = 22716/1716=15,804 = 22716/1716=15,804
Следовательно, уравнение тренда (регрессии) будет иметь вид:
y= 283,61+15,84t
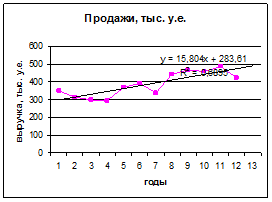
Доверительный интервал для линейного тренда находится по формуле:
ŷв.н. = ŷ(х0
) ± t1-
α
/2,
n
-2
Sŷ
,
где ув
, ун
– соответственно верхняя и нижняя границы
доверительногоинтервала;
ŷ(х0
) – точечный прогноз;
t1-
α
/2,
n
-2
–квантиль распределения Стьюдента;
(1-α/2) – доверительная верояность;
(n-2) – число степеней свободы;
ŷв.н. = ŷ(х0
) ± t1-
α
/2,
n
-2
Sŷ
,
ta
= 2,35
Доверительный интервал для уn
:
Нижняя граница интервала:
y= 300.29+13.24t = 300,29+13,24*293 = 4179,61
Верхняя граница интервала:
y= 300.29+13.24t= 300,29+13,24*488= 6761,41
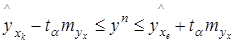
Sx1
2
= 1/n ∑(xi
- 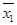 )2
= 51804,7/12 = 4317,06 )2
= 51804,7/12 = 4317,06
Sx1
= 65,704
zср = 386.33
| z |
zi
-
zср
|
(zi
-
zi
ср)
2
|
| 350 |
-36.33 |
1319,87 |
| 314 |
-72.33 |
5231,63 |
| 300 |
-86.33 |
7452,89 |
| 293 |
-93.33 |
8710,49 |
| 368 |
-18.33 |
335,99 |
| 393 |
6.67 |
44,49 |
| 339 |
-47.33 |
2240,13 |
| 443 |
56.67 |
3211,49 |
| 467 |
80.67 |
6507,65 |
| 457 |
70.67 |
4994,25 |
| 488 |
101.67 |
10336,79 |
| 424 |
37.67 |
1419,03 |
| 4636 |
24624 |
51804,7 |
myx
= S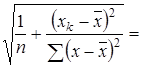 65,704*√1/12+ 24624/51804,7 = 36,71 65,704*√1/12+ 24624/51804,7 = 36,71
65,704 – 2,35*36,71 ≤ yn
≤ 65,704 + 2,35*36,71
Точечный прогноз среднего значения продаж по линейному тренду находится следующим образом:
ŷв.н. = 283,61+15,84*13 = 489,53
Окончательно получаем интервальный прогноз продаж
ŷв.н. = 489,5 ±2,353*36,71
Или ŷв= 489,5 ±2,353*36,71 = 575,89
Или ŷн= 489,5 ±2,353*36,71 = 403,12
Для регрессионных моделей:
y = а0
+ а1
х1
+ а2
х2
+ε
z1 =
а0
а1
t + а2
cos (2πt/12) + а3
sin (2πt/12) + εt
проверить наличие или отсутствие автокорреляции, используя критерий Дарбина-Уотсона при уровне значимости α = 0,05.
Для регрессионной модели y = а0
+ а1
х1
+ а2
х2
+ε
Проверить наличие или отсутствие мультиколлинеарности, используя критерии xи-квадрат (χ2
) при уровне значимости α = 0,05.
|