ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ПСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
Решение задач линейного программирования в среде
Maple
Курсовая работа
Студента 4 курса
физико-математического
факультета отделение «математика»
Гоняна Аршака Арзумановича
Научный руководитель
Матвеев Владимир Александрович
Псков
2008
Содержание
§1. Библиотека «simplex» пакета Maple
§2. Постановка задача линейного программирования для N переменных
§3. Постановка Транспортной задачи (ТЗ) для n переменных
§4. Пример решения задача линейного программирования
§5. Пример решения Транспортной задачи
Список литературы
§1. Библиотека «
simplex
» пакета
Maple
Библиотека «simplex» - предназначена для оптимизации линейных систем с использованием симплексного алгоритма. Особенность ее в том, что имеется возможность выполнять оценки промежуточных этапов симплексного алгоритма, например, определять базисные переменные и т.п.
После подключения библиотеки командой with(simplex) пользователю становится доступны функции и опции, указанные в следующей таблице.
| basis |
Находит базисные переменые |
| cterm |
Выводит список элементов вектора ресурсов |
| display |
Представляет систему в матричной форме |
| dual |
Преобразует данную задачу в двойственную задачу линейного программирования |
| feasible |
Возвращает true – если решение существует, и false – если нет |
| maximize |
Находит максимум целевой функции |
| minimize |
Находит минимум целевой функции |
| NONNEGATIVE |
Опция: указание на условие не отрицательности всех переменных |
| setup |
Приводит систему ограничений к стандартной форме |
| standardize |
Превращает систему ограничений в пары неравенств |
§2. Постановка задача линейного программирования для N переменных
Рассмотрим задачу формирования плана производства: некоторое предприятие может выпускать определённый набор продукции. Нормы затрат известны. Требуется построить производственный план, учитывающий ограниченность ресурсов в котором необходимо определить нормы выпуска каждого вида продукции, чтобы прибыль от её реализации была максимальной.
Построение экономико-математической модели
n - число различных видов продукции.
m - число различных ресурсов.
aij
- объём i-того ресурса, который расходуется на производство одной единици j-того вида продукции i=1..m, j=1..n.
Xj
- объем (количество единиц) j-того вида продукции в производственном плане предприятия (j от 1 до n).
Прибыль обозначим F, тогда F=c1
X1
+c2
X2
+...+cn
Xn
->=max
Составим ограничения для первого ресурса:
а11
- объем первого ресурса, который расходуется на производство одной единицы первого вида продукции;
а11
Х1
- объём первого ресурса, который требуется на изготовление Х1
единиц первого вида продукции;
а12
Х2
- объём первого ресурса, который требуется на изготовление Х2
единиц второго вида продукции;
а1n
Хn
- объём первого ресурса, который требуется на изготовление Хn
единиц n-ого вида продукции;
а11
Х1
+a12
X2
+...+a1n
Xn
- объём первого ресурса, который требуется на изготовление продукции, следовательно, мы имеем следующее ограничение:
а11
Х1
+а12
+...+а1n
Xn
<= b1
Аналогично для остальных ресурсов:
а21
Х1
+а22
+...+а2n
Xn
<=b2
а31
Х1
+а32
+...+а3n
Xn
<=b3
.........................................
аm1
Х1
+аm2
+...+amn
Xn
<=bm
Кроме того, количество выпущенной продукции не может быть отрицательной, следовательно, Х1
>= 0, X2
>=0, ...,Xn
>=0.
§3. Постановка Транспортной задачи (ТЗ) для
n
переменных
Пусть имеется несколько поставщиков однородной продукции (каждый с определенным запасом) и несколько потребителей этой продукции (с известными потребностями у каждого). Задана также сеть коммуникаций (дорог, рек, воздушных линий и т.д.) связывающая каждого поставщика с каждым потребителем. На каждой коммуникации задана цена перевозки – стоимость перевозки единицы продукции. Если какая – либо коммуникация отсутствует, то считаем, что она есть, но цену перевозки на ней устанавливаем равной бесконечности (+∞). Это соглашение сделает невыгодным перевозку по ней и автоматически исключит данную коммуникацию из плана перевозок.
Таким образом, требуется составить план перевозок продукции от поставщиков к потребителям так, чтобы потребности потребителей были бы удовлетворены за счет вывоза запаса от поставщиков. Цель – минимизация суммарной стоимости всех перевозок.
Транспортные задачи бывают:
1) открытые m ≠ n (суммарный запас продукции, имеющейся у поставщиков, не совпадает с суммарной потребностью в продукции у потребителей.)
2) закрытые m = n (суммарный запас продукции, имеющейся у поставщиков, совпадает с суммарной потребностью в продукции у потребителей.)
Метод потенциалов «работает» только для закрытых ТЗ, причем, закрытая ТЗ всегда разрешима.
Открытую ТЗ сводят к закрытой ТЗ путем прибавления к суммарному запасу продукции или суммарной потребности продукции недостающих единиц до равенства суммарного запаса продукции и суммарной потребности продукции.
Закрытая транспортная задача формулируется как Задача Линейного Программирования (ЗЛП) следующего вида:
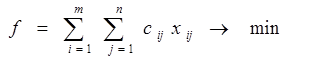
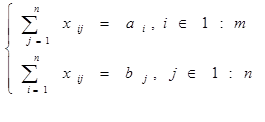
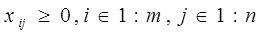 , где , где
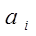 - запас i – го поставщика - запас i – го поставщика
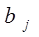 - потребность j – го потребителя - потребность j – го потребителя
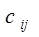 - цена перевозки единицы продукции по коммуникациям (i,j) - цена перевозки единицы продукции по коммуникациям (i,j)
(от i – го поставщика к j – му потребителю)
 - объем перевозки продукции (неизвестный) по коммуникациям (i,j). - объем перевозки продукции (неизвестный) по коммуникациям (i,j).
Для вывода критерии оптимальности транспортной задачи построим двойственную задачу.
Структура матрицы ограничений транспортной задачи такова, что столбец, соответствующей переменной  содержит ровно два ненулевых элемента: единицу в строке с номером i и единицу в строке m + i. содержит ровно два ненулевых элемента: единицу в строке с номером i и единицу в строке m + i.
Вектор двойственных переменных Y = (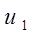 ,…, ,…,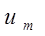 , ,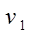 ,…, ,…,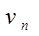 ) имеет m + n компонент (по числе ограничений ТЗ), которые называются потенциалами: переменные ) имеет m + n компонент (по числе ограничений ТЗ), которые называются потенциалами: переменные 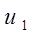 , , ,…, ,…,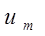 - потенциалы поставщиков; переменные - потенциалы поставщиков; переменные 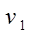 , ,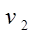 …, …,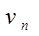 - потенциалы потребителей. - потенциалы потребителей.
Используя схему для построения двойственной задачи к ЗЛП в стандартной форме, имеем: 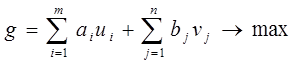
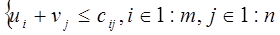
В полученной двойственной задаче n·m ограничений, соответствующих каждой переменной  ТЗ. Вспоминая, что невязка между левой и правой частью в ограничений двойственной задачи есть оценка для соответствующей переменной исходной задачи , запишем условия оптимальности текущего плана перевозок в ТЗ: ТЗ. Вспоминая, что невязка между левой и правой частью в ограничений двойственной задачи есть оценка для соответствующей переменной исходной задачи , запишем условия оптимальности текущего плана перевозок в ТЗ:
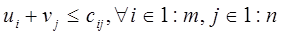 . .
Неизвестные потенциалы 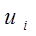 и и 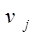 (их общее количество равно m + n) могут быть найдены (и именно так отыскиваются) из условия равенства нулю оценок для базисных переменных (заполненных клеток таблицы) ТЗ (таких равенств (m+n - 1), что следует из замечания ниже). (их общее количество равно m + n) могут быть найдены (и именно так отыскиваются) из условия равенства нулю оценок для базисных переменных (заполненных клеток таблицы) ТЗ (таких равенств (m+n - 1), что следует из замечания ниже).
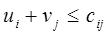 , ,
для заполненных клеток (i,j) таблицы ТЗ.
Решение полученной системы (содержащей неизвестных на единицу больше, чем число уравнений) ищется, когда одно из неизвестных (вообще говоря, любое) полагается равным некоторому числу (тоже, вообще говоря, любому). После этого оставшаяся система имеет единственное решение.
§4. Пример решения задача линейного программирования
Решим задачу линейного программирования симплекс – методом :
f(x) = 2
x
1
+ 3
x
2
+ 4
x
3
→ max
3x1
+ x2
+ 3x3
<=5
5
x
1
+ 4
x
2
+ 4
x
3
<=12
2
x
1
+
x
2
+ 2
x
3
<=8
x
1
>=0;
x
2
>=0;
x
3
>=0;
Данные задачи заносим в симплекс таблицу.
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
значения |
базис |
оценка |
| 3 |
1 |
3 |
1 |
0 |
0 |
5 |
x4 |
5/3 |
| 5 |
4 |
4 |
0 |
1 |
0 |
12 |
x5 |
3 |
| 2 |
1 |
2 |
0 |
0 |
1 |
8 |
x6 |
4 |
| 2 |
3 |
4 |
0 |
0 |
0 |
0 |
- f |
В этой таблице первая, вторая и третья строки соответствуют ограничениям задачи, последняя строка – функция цели. Это оценочная строка. Значение функции цели берём 0. Выделяем базисные переменные. Эта переменная находиться в столбце, для которой имеется одна единица, остальные нули. В столбце «базис» отмечаем одноимённые переменные в той строке, где расположена эта единственная единица. Остальные переменные называются свободными.
По заполненной симплекс таблице определяем решение, соответствующее этой (нулевой) итерации. Свободные переменные равны 0. Базисные переменные и значение функции находим из таблицы. Они представлены в столбце «значение». Отметим, что значение функции цели берём с противоположенным знаком. Итак, x° = (0,0,0,5,12,8) f° = 0.
В оценочной строке имеются положительные числа. Значит, решение можно улучшить. Выбираем наибольшее из положительных чисел. Если таких чисел несколько – берём любое из них. Соответствующий столбец называют ведущим. По ведущему столбу и столбцу «значения» определяем оценку для каждой строки. Число из столбца «значение» делим на строку. По условию задачи это положительное число. Объявляем ведущей строку ту, оценка у которой наименьшее положительное число.
В первой таблице ведущая строка и столбец выделен цветом. На их пересечении находится ведущий элемент. В нашем случае это 3.
Переходим к первой итерации. Её суть состоит в том, чтобы свободную x
3
сделать базисной, а базисную переменную x
4
-
свободной. В таблице выполняем преобразования аналогичные элементарным строчным преобразования аналогичные элементарным строчным преобразованиям в методе Гаусса при решении системы линейных уравнений. В результате преобразований получим:
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
значения |
базис |
оценка |
| 1 |
1/3 |
1 |
1/3 |
0 |
0 |
5/3 |
x3 |
5 |
| 1 |
8/3 |
0 |
-4/3 |
1 |
0 |
16/3 |
x5 |
2 |
| 0 |
1/3 |
0 |
-2/3 |
0 |
1 |
14/3 |
x6 |
14 |
| -2 |
5/3 |
0 |
-4/3 |
0 |
0 |
-20/3 |
- f |
Из таблицы находим базисные переменные и значение функции x¹= (0,0,5/3,0,16/3,14/3) f¹ = 20/3. Этот результат можно проверить. Полученные результаты должны удовлетворять функции цели в канонической (стандартной) задаче линейного програмирования. В оценочной строке имеются положительные числа. Значит, решение можно улучшить. Аналогично строим следующую таблицу:
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
значения |
базис |
оценка |
| 5/8 |
0 |
1 |
1/2 |
-1/8 |
0 |
1 |
x3 |
- |
| 3/8 |
1 |
0 |
-1/2 |
3/8 |
0 |
2 |
x2 |
- |
| -1/8 |
0 |
0 |
-1/2 |
-1/8 |
1 |
4 |
x6 |
- |
| -21/8 |
0 |
0 |
-1/2 |
-5/8 |
0 |
-10 |
- f |
f
* = 10
x
* = (0,2,1)
§5. Пример решения Транспортной задачи
Метод потенциалов представляет из себя модификацию симплекс-метода, учитывающую специфику транспортной задачи, поэтому его алгоритм не отличается от алгоритма симплекс-метода, за исключением шага проверки целевой функции на неограниченность на множестве решений. Отсутствие указанного шага в методе потенциалов обусловлено теоремой о том, что закрытая ТЗ всегда разрешима
. Итак, алгоритм метода потенциалов для решения ТЗ состоит из следующих шагов:
ШАГ 1. Построение начального плана перевозок.
ШАГ 2. Проверка текущего плана на оптимальность.
Если план оптимален, то алгоритм завершен.
ШАГ 3. Улучшение плана перевозок. Переход к шагу 1.
Опишем алгоритм по шагам, иллюстрируя каждый шаг
ШАГ 1. Построение начального плана перевозок.
Построение начального решения (как и последующие расчеты) проводят в таблице, имеющей следующий вид:

Клетка ( i , j ) таблицы соответствует коммуникации, связывающей i-го поставщика сj-м потребителем.
Построить начальный план перевозок означает - назначить объемы перевозок в клетки таблицы таким образом, чтобы:
а)число заполненных клеток было (m+n-1). (Тогда план перевозок будет отвечать базисному решению ЗЛП);
б)сумма перевозок в любой строке должна быть равна запасу соответствующего поставщика, а сумма перевозок в каждом столбце равна потребности потребителя. (Условие выполнения ограничений ТЗ). Существует несколько способов нахождения начального решения, которые отличаются только выбором клетки, в которую назначается очередная перевозка. Так, в способе северо-западного угла (СЗУ)
для очередного назначения перевозки выбирается левая верхняя клетка таблицы (при этом никак не учитываются цены перевозок). Наоборот, в способе минимальной стоимости (МС)
для заполнения выбирается клетка текущей таблицы с минимальной ценой перевозки, что в большинстве случаев (но не всегда) приводит к более дешевому (а значит и более близкому к оптимальному) начальному плану перевозок.
Мы будем пользоваться способом минимальной стоимости (МС).
Изложим теперь алгоритм нахождения начального решения
.
ШАГ 1
.
Определенным способом выбираем клетку в текущей таблице. Пусть она имеет индексы (i, j) (i -номер поставщика, j- номер потребителя).
ШАГ
2. В качестве перевозок в эту клетку назначаем наименьшую из ai
и потребности bj.
xij
= min{ai
,bj
}
ШАГ З. Уменьшим запас ai
и потребность bjна величину перевозки xij
,
т.е.
ai
= ai
- xij
,
bj =bj -xij
ШАГ 4. При исчерпании запаса (ai
= 0) запрещаем к перевозке оставшиеся свободные клетки i-ой строки, а при исчерпании потребности
(bj =0) запрещаем такие же клетки вj-ом столбце.
В случае одновременного исчерпания запасов потребностей (ai =bj= 0) запрещаем перевозки или в строке (тогда считаем, что у потребителя осталась потребность в количестве равном нулю, которую необходимо удовлетворить), или в столбце (в этом случае считаем, что у поставщика остается запас равный нулю, который необходимо вывезти). Это делается для того, чтобы при одновременном запрещении перевозок в строке и столбце количество заполненных клеток таблицы не стало меньшим, чем m+n-1.
Получим новую текущую таблицу, в которую не входят заполненные и запрещенные клетки. Если таблица не пуста, переходим к шагу 1. (При исчерпании таблицы - конец).
Способ минимальной стоимости

1.Клетки с минимальной ценой (3,1), (3,2) и (3,3). Выбираем, например, (3,2). (Далее все шаги, как в предыдущем способе).
2 . x32
= min{50,60} = 50
3. a'
3
=50-50=0, b'
2
= 100-50=50
4.Запрещаем строку 3.

1. Клетка с min ценой ~ (2,3)
2. x23
= min{70,80} = 70
3. a2
=70-70=0, b'3
= 80-70=10
4. Запрещаем строку 2.
| 1 |
2 |
3 |
| 60 |
5
60
|
10 |
12 |
| Χ |
8
-
|
6
-
|
4
70
|
Χ
|
0 |
0
50
|
0
-
|
| 50 |
10 |
1. Клетка с min ценой ~ (1,1)
2. x 11
=min{120,60} = 60
3. a 1'
=120-60 = 60, b1'
= 0
4.В первом столбце запрещать уже нечего. Текущая таблица содержит две клетки (1,2) и (1,3).

1.Выбираем клетку (1,2)
2
.
x12
=min{110,100} = 100
3.a1
=110-100 = 10, b'
1
= 0
4.Текущая таблица содержит одну клетку (1,3).

1. Выбираем последнюю клетку(1,3)
2. x13
=min{10,10} = 10
3.a1
'
= b3
= 0
4.Таблица исчерпана. Конец.
Переходим к описанию следующего шага метода потенциалов.
ШАГ 2.
Проверка текущего плана на оптимальность.
Признаком того, что текущий план перевозок является оптимальным, служит условие
(1)ui
+vj -cij
≤0
которое выполняется для всех клеток таблицы. Неизвестные здесь величины ui
и vj(называемые потенциалами) определяются из условий
(2)ui
+ vj
= cij
Условие (1) означает невозможность появления "спекулятивной" цены. Само же название "потенциалы" заимствовано из физического закона о том, что работа по перемещению заряда в электростатическом поле равна разности потенциалов в данных точках поля (У нас: "...цена перевозки единицы продукции по коммуникации равна разности цен в конце и в начале пути")
Так как заполненных клеток в таблице (m+n-1) штук, а неизвестных и (m+n) штук, то для их определения имеется система из (m+n-1) уравнений относительно (m+n) неизвестных. Чтобы найти решение (хотя бы какое-нибудь) такой системы, достаточно положить одно из неизвестных (произвольное) равным некоторому произвольно выбранному числу. Тогда остальные определяются единственным образом. Можно решать эту систему непосредственно (продолжаем работать с нашим "старым" примером и найдем потенциалы для начального плана, построенного способом МС).
Заполненные клетки Уравнения
(1,1) u1
+ v1
=5
(1,2) u1
+ v2
=10
(1,3) u1
+ v3
=12
(2,3) u2
+v3
=4
(3,2) u3
+v2
=0
Положим, например, неизвестное u1
равным 0 (через него можно из первых трех уравнений найти v1
, v2
и v3
). Последовательно из них находим u2 ,
u3.
Этот метод можно сформулировать в виде единой правилы:
Неизвестный потенциал находится вычитанием известного из цены перевозки в заполненной клетке
Применим это правило для определения u и vв нашем примере и получим:
u1
=0, u2
=-8, u3
=-6
v1
=5, v2
=10, v3
=12
Переходим к проверке условий оптимальности (1). Достаточно проверять их для незаполненных клеток, так как для клеток заполненных эти условия выполняются как равенства. Для проверки берется незаполненная клетка, складываются соответствующие ей потенциалы (первый элемент строки и последний элемент столбца) и из них вычитается цена перевозки в данной клетке. Если полученное число отрицательное (или ноль), то оптимальность в данной клетке не нарушается (в случае выполнения условия (1) для всех незаполненных клеток, имеем оптимальный план перевозок). Если же в таблице встретилась хотя бы одна клетка, для которой это число положительно, тогда решение не является оптимальным и может быть улучшено.
Проверим на оптимальность имеющееся решение
(2,1)u2
+v1
-c21
=-8+5-8=-11<0
(2,2) u 2
+v2
-c22
=-8+10-6=-4<0
(3,1)u3
+v1
-c31
=-10+ 5-0=-5<0
(3,3)u3
+v3
-c33
=-10+12-0=2>0
Следовательно, условие оптимальности нарушено в клетке (3,3).
Имеющийся план перевозок можно улучшить.
Дадим описание заключительного шага алгоритма метода потенциалов.
ШАГ 3
Улучшение плана перевозок
.
Улучшение плана происходит путем назначения перевозки θ>0 в ту клетку (i , j) таблицы, в которой нарушилось условие оптимальности. Но назначение ненулевой перевозки нарушает условия баланса вывоза продукции от поставщика i (вывозит весь запас и еще плюсθ>0 ) и условия баланса привоза продукции к потребителю j(получает все что можно и еще плюс θ > 0). Условия баланса восстанавливают путем уменьшения вывоза от i-поставщика к какому-то другому потребителю j(уменьшают на θ перевозку в какой-то заполненной клетке (i , j) строки i). При этом нарушается баланс привоза продукции к потребителю j (получает на θ меньше, чем ему требуется). Восстанавливают баланс в столбце j, тогда он нарушается в некоторой строке i и т.д. до тех пор, пока цикл перемещения перевозок не замкнется на клетке, в которой нарушалось условие оптимальности. Продемонстрируем эти рассуждения на нашем примере.

| 120 |
60 |
50+ Ө |
10- Ө |
| 70 |
- |
- |
70 |
| 50 |
- |
50- Ө |
* + Ө |
| 60 |
100 |
80 |
| 120 |
60 |
60 |
-(0) |
| 70 |
- |
- |
70 |
| 50 |
- |
40 |
* 10 |
| 60 |
100 |
80 |
1. Оптимальность нарушена в клетке (3,3). Назначим в нее перевозку θ>0 (+θ означает, увеличение на θ).
2.Нарушается баланс вывоза от поставщика 3 (вывозит 50+ θ, а это больше его запаса!). Уменьшаем на θ перевозку в заполненной клетке строки 3 (вне заполненной уменьшать нельзя, так как это приведет к отрицательной перевозке).
Рассмотрим те клетки цикла в которых уменьшаем на θ перевозку и берём минимум из вычетаемых, у нас это min{10- θ ,50- θ }=10.
И данное число надо подставить в цикл
Список литературы
1. Матвеев В.А. Конечные бескоалиционные игры и равновесия. Псков, 2004,176с.
2. Аладьев В.З., Богдявичюс М.А. MAPLE 6: Решение математических, статистических и физико – технических задач – М.: Лаборатория Базовых Знаний,2001 – 824с..
3. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр. М.:ВШ, Книжный дом «Университет», 1998.
4. Акулич И.Л. Математическое программирование в примерах и задачах. М.: Высшая школа, 1993.
5. Воробьёв Н.Н. Основы теории игр. Бескоалиционные игры. М.: Наука, 1984.
6. Прохоров Г.В., Колбеев В.В., Желнов К.И., Леденев М.А..Математический пакет MapleVRelease 4. М. 1998.
|