Курсова робота
Рішення ірраціональних рівнянь
Введення
Тема моєї курсової роботи рішення ірраціональних рівнянь. Я вибрала її тому, що в навчальному курсі, цьому матеріалу присвячено мало годин, а в задачниках велика кількість прикладів присвячена саме цій темі.
Тому у вивченні «ірраціональних рівнянь» я маю на меті - дати основні визначення ірраціональним рівнянням і теоремам. Визначити які бувають види рівнянь. Розглянути правила рішення ірраціональних рівнянь.
Задачі моєї роботи - вивчити наукову й методичну літературу, підібрати й розглянути задачі для даної теми.
У моїй курсовій роботі показані рішення ірраціональних рівнянь як стандартного методу, так і не стандартного методу рішення. Я намагалася як можна доступніше охопити проблеми цієї теми. Звичайно, всі не можна врахувати в курсовій роботі, але я постараюся нижче викласти основні моменти. Я хотіла б зробити дану роботу допоміжним посібником при вивченні теми «Ірраціональні рівняння».
1. Основні визначення й теореми
Визначення 1. Рівняння - це два вираження, з'єднані знайомий рівності; у ці вираження входить одна або трохи змінних, називаних невідомими.
Приклад 1
. 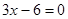 - є рівнянням з однієї невідомої. - є рівнянням з однієї невідомої.
Приклад 2.
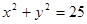 - є рівнянням із двома невідомими. - є рівнянням із двома невідомими.
Визначення 2. Рівність виду  називається рівнянням з однієї змінної називається рівнянням з однієї змінної 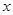 . .
Приклад 1.
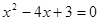 - є рівнянням з однієї змінної х. - є рівнянням з однієї змінної х.
Далі розглядаємо рівняння з однієї змінної.
Визначення 3. Усяке значення змінної, при якому вираження  й й 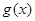 приймають рівні числові значення, називається коренем рівняння або його рішенням. приймають рівні числові значення, називається коренем рівняння або його рішенням.
Приклад 1.
Рівняння 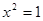 має два корені: -1 і 1. має два корені: -1 і 1.
Визначення 4. Вирішити рівняння - виходить, знайти множину всіх його рішень або довести, що їх немає.
Приклад 1.
Рівняння 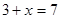 має єдиний корінь 4, тому що при цьому й тільки при цьому значенні змінної має єдиний корінь 4, тому що при цьому й тільки при цьому значенні змінної 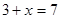 звертається у вірну рівність, таким чином, відповідь записується в наступному виді: звертається у вірну рівність, таким чином, відповідь записується в наступному виді:
Відповідь: {4}.
Приклад 2.
Рівняння  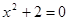 не має дійсних корінь. не має дійсних корінь.
Відповідь: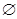 . .
Приклад 3.
Рівняння 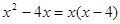 має нескінченна множина рішень, тому що після тотожних перетворень одержали рівність має нескінченна множина рішень, тому що після тотожних перетворень одержали рівність 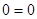 . Дане рівняння . Дане рівняння 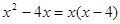 є тотожна рівність, вірне для будь-якого дійсного значення є тотожна рівність, вірне для будь-якого дійсного значення 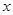 . .
Відповідь: 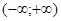 . .
Визначення 5. Тотожність (тотожна рівність) - це рівність двох виражень зі змінними, вірне при всіх припустимих значеннях вхідних у нього змінних. Тотожностями вважаються й вірні числові рівності, а також рівності, що перетворюються у вірну числову рівність для всіх числових значень букв, для яких ці вираження визначені.
Приклад 1.
Рівність 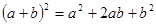 , справедливо для всіх числових значень , справедливо для всіх числових значень 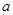 і в, є тотожним. і в, є тотожним.
Приклад 2.
Рівність 2=2 тотожність.
Визначення 6. Тотожне перетворення вираження - це заміна вираження на тотожно рівне йому вираження, тобто рівне для всіх числових значень вхідних у нього змінних.
До тотожних перетворень ставляться, наприклад, приведення подібних доданків; розкладання на множники; приведення алгебраїчних дробів до загального знаменника; розкладання їх на елементарні дроби й інші.
Визначення 7. Ірраціональним називають рівняння, у якому змінна втримується під знаком радикала або під знаком введення в дробовий ступінь.
Приклад 1.
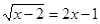 - ірраціональне рівняння (змінна втримується під знаком радикала). - ірраціональне рівняння (змінна втримується під знаком радикала).
Приклад 2.
 ірраціональне рівняння (змінна втримується під знаком введення в дробовий ступінь). ірраціональне рівняння (змінна втримується під знаком введення в дробовий ступінь).
Визначення 8. Областю визначення рівняння (або областю припустимих значень змінної - ОПЗ)  називають множина всіх тих значень змінної називають множина всіх тих значень змінної 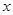 , при яких і вираження , при яких і вираження  , і , і 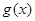 мають сенс. мають сенс.
Приклад 1.
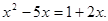 Вираження ( Вираження (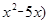 і і 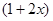 визначені при всіх визначені при всіх 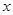 . Виходить, ОПЗ: . Виходить, ОПЗ: 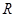 . .
Приклад 2.
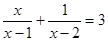 . Вираження . Вираження 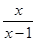 не визначене при не визначене при  , а вираження , а вираження 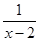 не визначене при не визначене при 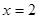 . .
Виходить, ОПЗ: 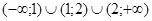 . .
Приклад 3.
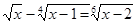 . Корінь парного ступеня має сенс лише при ненегативних значеннях підкореневого вираження. Виходить, одночасно повинні виконуватися умови: . Корінь парного ступеня має сенс лише при ненегативних значеннях підкореневого вираження. Виходить, одночасно повинні виконуватися умови: 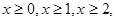 тобто ОПЗ: тобто ОПЗ: 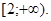
Визначення 9. Нехай дані рівняння: 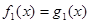 (1), (1), 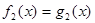 (2). (2).
Якщо кожний корінь рівняння (1) є одночасно коренем рівняння (2), то рівняння (2) називається наслідком рівняння (1). Наслідок позначається в такий спосіб:  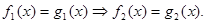
Приклад 1.
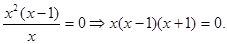
У процесі рішення рівняння часто доводиться застосовувати такі перетворення, які приводять до рівняння, що є наслідком вихідного. Рівнянню-Наслідку задовольняють всі корені вихідного рівняння, але, крім них, рівняння-наслідок може мати й такі рішення, які не є коріннями вихідного рівняння, так звані, «сторонні» корені. Щоб виявити й відсіяти «сторонні» корінь, звичайно надходять так: всіх знайдених корінь рівняння-наслідку перевіряють підстановкою у вихідне рівняння.
Розглянемо приклади перетворень, які можуть привести до розширення ОПЗ, тобто до появи «сторонніх» корінь.
Заміна рівняння 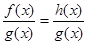 рівнянням рівнянням 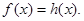
Якщо при деякому значенні 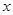 , рівному , рівному 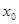 , вірне рівність , вірне рівність 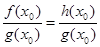 , то вірним є також рівність , то вірним є також рівність 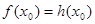 . Виходить, рівняння . Виходить, рівняння 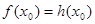 є наслідком вихідного рівняння. При цьому може існувати таке значення є наслідком вихідного рівняння. При цьому може існувати таке значення 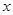 , рівне , рівне 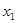 , при якому , при якому 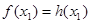 й й 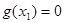 . Тоді число . Тоді число 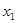 , що є коренем рівняння , що є коренем рівняння 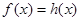 , не є коренем вихідного рівняння, тому що при , не є коренем вихідного рівняння, тому що при 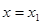 вихідне рівняння не має змісту. вихідне рівняння не має змісту.
Приклад 1.
Вирішити рівняння 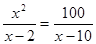 . .
Рішення. 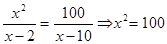 . Тоді . Тоді 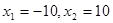 . .
Перевірка.
При 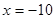 знаменник рівняння не звертається в нуль, а при знаменник рівняння не звертається в нуль, а при 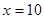 - звертається. Отже, вихідне рівняння має єдиний корінь: -10. - звертається. Отже, вихідне рівняння має єдиний корінь: -10.
Відповідь: 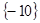 . .
2. Введення обох частин рівняння у квадрат
Нехай дані два рівняння  (1) і (1) і  . Якщо . Якщо 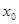 - корінь першого рівняння, то вірно рівність - корінь першого рівняння, то вірно рівність 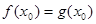 . З рівності двох чисел випливає рівність їхніх квадратів, тобто . З рівності двох чисел випливає рівність їхніх квадратів, тобто 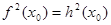 , а це означає, що , а це означає, що 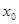 - корінь рівняння (2). Значить із рівняння (1) потрібне рівняння (2). - корінь рівняння (2). Значить із рівняння (1) потрібне рівняння (2).
У той же час із рівності квадратів чисел не потрібне рівність цих чисел. Тому з рівняння (2) не потрібне рівняння (1). Звідси випливає, що якщо при рішенні рівняння використовувалося введення обох частин рівняння у квадрат, те потрібно повести додаткове дослідження, що дозволяє виключити «сторонні» корені, якщо вони з'явилися.
Приклад 1.
Вирішити рівняння 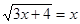 . .
Рішення. Зведемо обидві частини цього рівняння у квадрат.
 ; ; 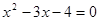 .Тоді .Тоді 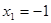 , , 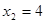 . .
Перевірка.
Якщо 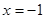 , те , те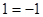 , рівність не вірно, отже, -1- не є коренем вихідного рівняння. , рівність не вірно, отже, -1- не є коренем вихідного рівняння.
Якщо 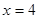 , то 4=4, рівність вірно. , то 4=4, рівність вірно.
Отже, рівняння має єдиний корінь: 4.
Відповідь: {4}.
3. Виконання в одній частині (або в обох частинах) рівняння тотожних перетворень, що приводять до розширення області визначення рівняння.
Якщо деяке тотожне перетворення привело до розширення області визначення рівняння, то одержуємо рівняння - наслідок. При цьому можуть існувати такі значення змінної, які є коріннями вихідного рівняння.
Приклад 1.
Вирішити рівняння 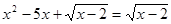 . .
Рішення. Виконавши приведення подібних доданків, одержимо:  . Тоді . Тоді  , , 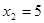 . .
Перевірка.
Якщо 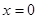 , то вираження , то вираження  не має змісту. не має змісту.
Якщо 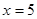 , те , те , рівність вірно. , рівність вірно.
Отже, рівняння має єдиний корінь:5.
Відповідь: {5}.
Приклад 2.
Вирішити рівняння 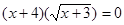 . .
Рішення. 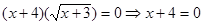 або або 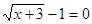 . Тоді . Тоді 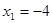 , , 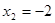 . .
Перевірка.
Якщо 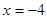 , то вираження , то вираження 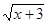 не має змісту. не має змісту.
Якщо 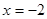 , те , те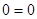 , рівність вірно. , рівність вірно.
Отже, рівняння має єдиний корінь:-2.
Якщо при рішенні рівняння ми замінили його рівнянням - наслідком, то зазначена вище перевірка є невід'ємною частиною рішення рівняння. Тому важливо знати, при яких перетвореннях дане рівняння переходить у наслідок.
Розглянемо рівняння  (3) і помножимо обидві частини його на одне й теж вираження (3) і помножимо обидві частини його на одне й теж вираження 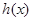 , що має зміст при всіх значеннях , що має зміст при всіх значеннях 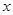 . Одержимо рівняння: . Одержимо рівняння: 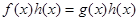 (4), коріннями якого служать як коріння рівняння (3), так і корінь рівняння (4), коріннями якого служать як коріння рівняння (3), так і корінь рівняння 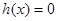 . .
Виходить, рівняння (4) є наслідок рівняння (3). Ясно, що рівняння (3) і (4) рівносильні, якщо «стороннє» рівняння 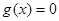 не має корінь. Таким чином, справедлива наступна теорема. не має корінь. Таким чином, справедлива наступна теорема.
Теорема 1. Якщо обидві частини рівняння помножити на 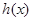 , то вийде рівняння, що є наслідком вихідного. Якщо рівняння , то вийде рівняння, що є наслідком вихідного. Якщо рівняння 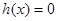 не має корінь, то отримане рівняння рівносильне вихідному (якщо область припустимих значень не має корінь, то отримане рівняння рівносильне вихідному (якщо область припустимих значень 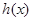 не вже області припустимих значень змінної даного рівняння). не вже області припустимих значень змінної даного рівняння).
Приклад 1.
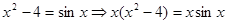 . .
Помітимо, що подібне перетворення, тобто перехід від рівняння (4) до рівняння (3) діленням обох частин рівняння (4) на вираження 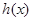 , як правило, неприпустимо, оскільки можна привести до втрати корінь, у цьому випадку можуть «втратитися» коріння рівняння , як правило, неприпустимо, оскільки можна привести до втрати корінь, у цьому випадку можуть «втратитися» коріння рівняння 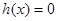 . .
Приклад 2.
Рівняння  має два корені: 3 і 4. має два корені: 3 і 4.
Ділення обох частин рівняння на 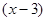 приводить до рівняння приводить до рівняння 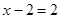 , що має тільки один корінь 4, тобто відбулася втрата кореня. , що має тільки один корінь 4, тобто відбулася втрата кореня.
Знову візьмемо рівняння (3) і зведемо обидві його частини у квадрат. Одержимо рівняння: 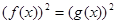 (5), коріннями якого служать як коріння рівняння (3), так і корінь «стороннього» рівняння (5), коріннями якого служать як коріння рівняння (3), так і корінь «стороннього» рівняння 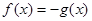 . Ясно, що рівняння (3) і (5) рівносильні, якщо в «стороннього» рівняння немає кореню. . Ясно, що рівняння (3) і (5) рівносильні, якщо в «стороннього» рівняння немає кореню.
Приклад 3.
Рівняння 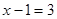 має корінь 4. Якщо обидві частини цього рівняння піднести до квадрата, то вийде рівняння має корінь 4. Якщо обидві частини цього рівняння піднести до квадрата, то вийде рівняння 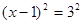 , що мають два корені: -2 і 4. Виходить, рівняння , що мають два корені: -2 і 4. Виходить, рівняння 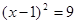 - наслідок рівняння - наслідок рівняння 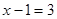 . При переході від рівняння . При переході від рівняння 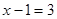 до рівняння до рівняння 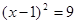 з'явився «сторонній» корінь: -2. з'явився «сторонній» корінь: -2.
Теорема 2. При піднесенні обох частин рівняння у квадрат (і взагалі в будь-який парний ступінь) виходить рівняння, що є наслідком вихідного.
Приклад 1.
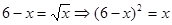 . .
При рішенні ірраціонального рівняння найчастіше намагаються замінити його більше простим, але рівносильним вихідному. Тому важливо знати рівносильні перетворення.
Визначення 10. Рівняння, що має ті самі корінь, називають рівносильними рівняннями. Рівняння, що не мають корінь, також уважають рівносильними. Іншими словами два рівняння називають рівносильними, якщо множини їхніх рішень збігаються. Рівносиль позначається в такий спосіб: 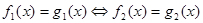 . .
Приклад 1.
Рівняння 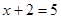 й й 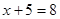 рівносильні, тому що кожне з них має єдиний корінь – число 3. рівносильні, тому що кожне з них має єдиний корінь – число 3. 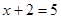 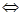 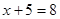 . .
Приклад 2.
Рівняння 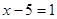 й й 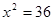 не рівносильні, тому що перше має тільки один корінь: 6, а друге має два корені: 6 і -6. не рівносильні, тому що перше має тільки один корінь: 6, а друге має два корені: 6 і -6.
Приклад 3.
Рівняння 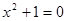 й й 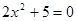 рівносильні, тому що множини їхніх рішень порожні. рівносильні, тому що множини їхніх рішень порожні. 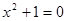 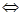 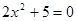 . .
Визначення 11. Нехай дані рівняння 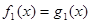 й й 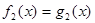 і деяка множина М. Якщо будь-який корінь першого рівняння, що належить множині М, задовольняють другому рівнянню, а будь-який корінь другого рівняння, що належить множині М, задовольняє першому рівнянню, те ці рівняння називаються рівносильними на множині М. і деяка множина М. Якщо будь-який корінь першого рівняння, що належить множині М, задовольняють другому рівнянню, а будь-який корінь другого рівняння, що належить множині М, задовольняє першому рівнянню, те ці рівняння називаються рівносильними на множині М.
Приклад 1.
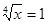 і і 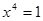 не є рівносильними на множині всіх дійсних чисел, тому що перше рівняння має єдиний корінь 1, а друге має два корені: -1 і 1. Але ці рівняння рівносильні на множині всіх ненегативних чисел, тому що кожне з них має на цій множині єдиний корінь: 1. не є рівносильними на множині всіх дійсних чисел, тому що перше рівняння має єдиний корінь 1, а друге має два корені: -1 і 1. Але ці рівняння рівносильні на множині всіх ненегативних чисел, тому що кожне з них має на цій множині єдиний корінь: 1.
Відзначимо, що часто множину М збігається або з ОПЗ рівняння  , або множиною всіх дійсних чисел. , або множиною всіх дійсних чисел.
Є ряд теорем про рівносиль рівнянь.
Теорема 3. При піднесенні обох частин рівняння в ту саму непарний ступінь виходить рівняння, рівносильне вихідному.
Приклад 1.
 . .
Теорема 4. Якщо в рівнянні який-небудь доданок перенести з однієї частини в іншу, змінивши його знак, то вийде рівняння, рівносильне вихідному.
Приклад 1.
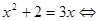 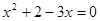 . .
Теорема 5. Якщо обидві частини рівняння помножити або розділити на одне й теж відмінне від нуля число, то вийде рівняння, рівносильне вихідному.
Приклад 1.
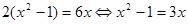 (обидві частини першого рівняння розділили на 2). (обидві частини першого рівняння розділили на 2).
Теорема 6. Якщо в який або частини рівняння виконати тотожні перетворення, що не міняють області визначення рівняння, то вийде рівняння, рівносильне вихідному.
У шкільній практиці при рішенні ірраціональних рівнянь найчастіше використовуються два основних методи:
1) обох частин рівняння в ту саму ступінь;
2) введення нових (допоміжних) змінних.
Ці методи будемо вважати стандартними. В обов'язковому шкільному курсі звичайно цими методами й обмежуються. Однак іноді доводиться застосовувати нестандартні методи й штучні прийоми рішення ірраціональних рівнянь.
Типова помилка при рішенні ірраціональних рівнянь полягає в тому, що школярі без додаткових пояснень використовують перетворення, що порушують рівносиль, що приводить до втрати кореня і появі «сторонніх» коренів.
При піднесенні обох частин ірраціонального рівняння в ту саму ступінь потрібне мати на увазі, що якщо ступінь - не парне число, то одержимо рівносильне рівняння, якщо ж ступінь - парне число, то одержимо рівняння - наслідок. Тому при рішенні ірраціональних рівнянь у більшості випадків необхідна перевірка знайдених рішень.
Перевірки можна уникнути, якщо вирішувати ірраціональні рівняння за допомогою рівносильних замін. Для цього корисно знать наступні теореми.
Теорема 7. Рівняння виду  рівносильне змішаній системі рівносильне змішаній системі 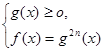
Рівняння виду 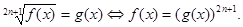
Теорема 8. Рівняння виду 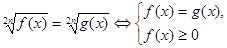 або або 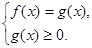 . .
Рівняння виду 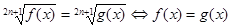 . .
Далі розглянемо більш докладно типи ірраціональних рівнянь і методи їхнього рішення.
2. Стандартні ірраціональні рівняння
Як правило, у шкільному курсі розгляд ірраціональних рівнянь зводиться до розбору декількох нескладних прикладів. Вони в більшості випадків вирішуються введенням у квадрат лівої й правої частин рівняння. Після рішення обов'язково виконується перевірка. Не звертається увага на те, що ірраціональні рівняння можуть вирішуватися й з використанням поняття рівносиль. У даному параграфі представлені різні види ірраціональних рівнянь, які можна віднести до стандартного й вирішувати одним з наступних методів, а саме:
1) метод переходу до рівняння - наслідку з наступною перевіркою отриманих корінь;
2) метод рівносильного переходу до рівняння або до змішаної системи;
3) метод введення нової змінної.
2.1 Рівняння виду 
Приклад 1.
Вирішити рівняння 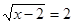 . .
Рішення. Зведемо обидві частини вихідного рівняння у квадрат.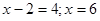 . .
Відповідь: {6}.
Приклад 2.
Вирішити рівняння 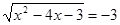 . .
Рішення. У лівій частині вихідного рівняння коштує арифметичний квадратний корінь - він по визначенню ненегативний, а в правій частині - негативне число.
Отже, рівняння не має кореня.
Відповідь: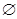 . .
Запишемо рівносиль, за допомогою якої вирішуються рівняння даного виду.
 , якщо , якщо 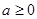 й не має рішення, якщо й не має рішення, якщо  . .
Приклад 3.
Вирішити рівняння 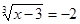 . .
Рішення. Зведемо обидві частини вихідного рівняння в куб.
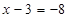 ; ; 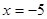 . .
Відповідь: {-5}.
Запишемо рівносиль, за допомогою якої вирішуються рівняння даного виду: 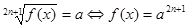 . .
2.2 Рівняння виду 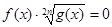
Досить часто при рішенні рівнянь даного виду учні використовують наступне формулювання властивості добутку «Добуток двох співмножників дорівнює нулю, коли хоча б один з них дорівнює нулю». Помітимо, що формулювання властивості добутку повинна виглядати в такий спосіб: « добуток двох співмножників дорівнює нулю, коли хоча б один з них дорівнює нулю, а іншої при цьому має сенс».
Запишемо рівносиль, за допомогою якої вирішуються рівняння даного виду:
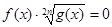 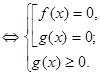
Приклад 1.
Вирішити рівняння  . .
Рішення.
 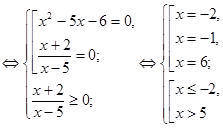 . .
Відповідь: {-2;6}.
Приклад 2.
Вирішити рівняння 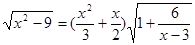 . .
Рішення. У цьому випадку рівняння не має виду, зазначеного в заголовку. Отже, його необхідно перетворити. Але спочатку знайдемо ОПЗ змінної 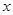 . .
ОПЗ:  
Перетворимо рівняння до виду 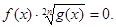
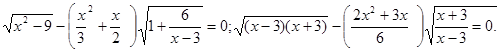
При рішенні рівняння учні часто необґрунтовано ділять обидві частини рівняння на вираження, що містить невідоме (у цьому випадку, на 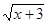 ), що приводить до втрати кореня й придбанню «стороннього». Подібні рівняння, що містять в обох частинах загальний множник, варто вирішувати переносом всіх членів в одну частину й розкладанням отриманого вираження на множники. ), що приводить до втрати кореня й придбанню «стороннього». Подібні рівняння, що містять в обох частинах загальний множник, варто вирішувати переносом всіх членів в одну частину й розкладанням отриманого вираження на множники.
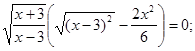 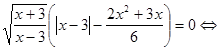 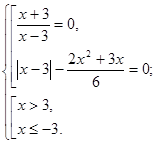
Вирішимо кожне рівняння із сукупності.
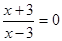 ; ;  . .
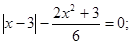  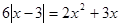 (1). (1).
З огляду на, що ОПЗ: 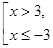 одержуємо, що рівняння (1) рівно сильно сукупності: одержуємо, що рівняння (1) рівно сильно сукупності: 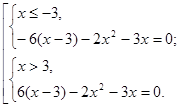
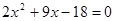 . Тоді . Тоді 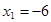 , , 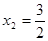 не задовольняє умові не задовольняє умові 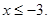
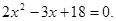 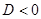 , дане рівняння не має корінь. , дане рівняння не має корінь.
Отже, сукупність прийме наступний вид: 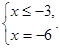
Повернемося до системи: 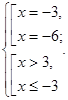
Відповідь: {-3;6}.
2.3 Ірраціональні рівняння, які вирішуються введенням нової змінної
При рішенні різних видів рівнянь: раціональних, тригонометричних, показових часто використовується метод введення нової змінної. Нова змінна в рівняннях іноді дійсно очевидна, але іноді її важко побачити, а можна виявити тільки лише в процесі яких або перетворень. Буває корисно ввести не одну, а дві змінні. Бачимо типові випадки введення нових змінних в ірраціональних рівняннях.
Приклад 1.
Вирішити рівняння 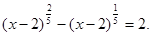
Рішення. Уведемо нову змінну. Нехай 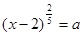 , ,  , де , де 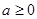 . Одержуємо, що . Одержуємо, що 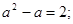 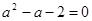 .Тоді .Тоді 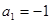 - не задовольняє умові - не задовольняє умові 
Виконаємо зворотну заміну. 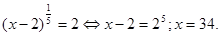
Відповідь:{34}.
Приклад 2.
Вирішити рівняння 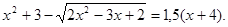
Рішення. Самота радикала й введення в ступінь обох частин рівняння привело б до громіздкого рівняння. У той же час, якщо виявити деяку спостережливість, то можна помітити, що дане рівняння зводитися до квадратного. Дійсно, помножимо обидві частини заданого рівняння на 2, одержимо, що 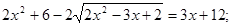 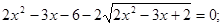 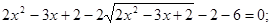 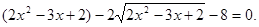
Уведемо нову змінну. Нехай 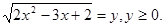 Одержуємо, що Одержуємо, що 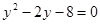 . Тоді . Тоді 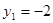 - не задовольняє умові - не задовольняє умові 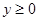 , , 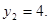
Виконаємо зворотну заміну.  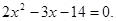 Тоді Тоді 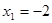 , , 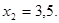
Так як вихідне рівняння рівносильне рівнянню  те перевірка отриманих корінь не потрібна. те перевірка отриманих корінь не потрібна.
Відповідь: {-2;3,5}.
Приклад 3.
Вирішити рівняння 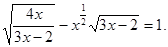
Рішення. Перетворимо дане рівняння. 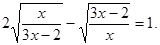 
Уведемо нову змінну. Нехай, 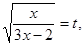 а а 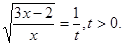 Одержуємо, що Одержуємо, що 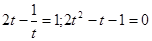 . Тоді . Тоді 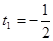 - не задовольняє умові - не задовольняє умові 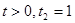 . .
Виконаємо зворотну заміну. 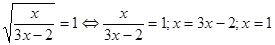 . .
2.4 Рівняння виду 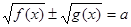 , , 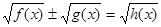 , ,
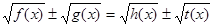
Дані рівняння можна вирішити за допомогою основного методу рішення ірраціональних рівнянь (введення у квадрат обох частин рівняння), але іноді їх можна вирішити й іншими методами.
Розглянемо рівняння 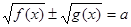 (1). Нехай (1). Нехай 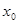 - корінь рівняння (1). Тоді справедливо числова рівність - корінь рівняння (1). Тоді справедливо числова рівність 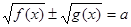 . Знайдемо різницю чисел . Знайдемо різницю чисел 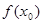 і і 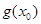 , позначивши її , позначивши її 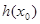 , і запишемо дану рівність у вигляді , і запишемо дану рівність у вигляді 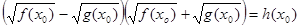 (2). (2).
Використовуючи, що 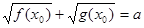 , запишемо рівність (2) у вигляді , запишемо рівність (2) у вигляді 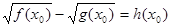 . Дана рівність означає, що число . Дана рівність означає, що число 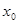 є корінь рівняння є корінь рівняння 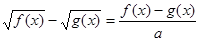 (3). (3).
Таким чином, рівняння (3) є наслідком рівняння (1). Складаючи ці два рівняння й множачи отримане рівняння на а, одержимо рівняння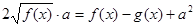 (4), що також є наслідком рівняння (1). Звівши рівняння (4) у квадрат і вирішивши отримане рівняння, потрібне виконати перевірку знайдених корінь, тобто перевірити, чи є його коріння коріннями рівняння (1). (4), що також є наслідком рівняння (1). Звівши рівняння (4) у квадрат і вирішивши отримане рівняння, потрібне виконати перевірку знайдених корінь, тобто перевірити, чи є його коріння коріннями рівняння (1).
Зауваження. Відзначимо, що точно також доводиться, що рівняння (4) є наслідок рівняння 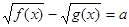 . .
Приклад 1.
Вирішити рівняння 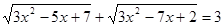 (5). (5).
Рішення. Різниця підкореневих виражень 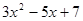 і і  є є
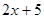 . . 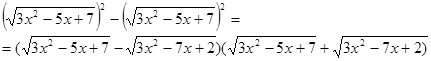 , ,
те рівняння 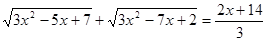 (6) є наслідком вихідного рівняння. Тоді, складаючи рівняння (5) і (6), одержимо рівняння (6) є наслідком вихідного рівняння. Тоді, складаючи рівняння (5) і (6), одержимо рівняння 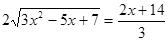 (7), що також є наслідком вихідного рівняння (5). Зведемо обидві частини рівняння (6) у квадрат, одержимо рівняння (7), що також є наслідком вихідного рівняння (5). Зведемо обидві частини рівняння (6) у квадрат, одержимо рівняння 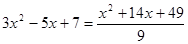 (8), що також є наслідком вихідного рівняння. Вирішуючи рівняння (8), одержуємо, що (8), що також є наслідком вихідного рівняння. Вирішуючи рівняння (8), одержуємо, що 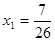 , , 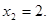
Перевіркою переконуємося, що обоє цих числа є коріннями вихідного рівняння.
Відповідь: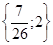 . .
Зауваження. Рівняння виду 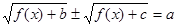 можна вирішувати множенням обох частин рівняння на деяке вираження, що не приймає значення нуль (на сполучене лівій частині рівняння тобто можна вирішувати множенням обох частин рівняння на деяке вираження, що не приймає значення нуль (на сполучене лівій частині рівняння тобто 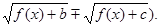
Приклад 2.
Вирішити рівняння 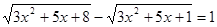 (8). (8).
Рішення. 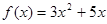 , те помножимо обидві частини рівняння на вираження , те помножимо обидві частини рівняння на вираження 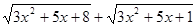 , що є сполученим лівої частини рівняння (8). , що є сполученим лівої частини рівняння (8). 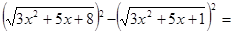 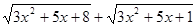 . Після приведення подібних доданків одержуємо рівняння . Після приведення подібних доданків одержуємо рівняння  (9), рівносильне вихідному, тому що рівняння (9), рівносильне вихідному, тому що рівняння 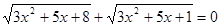 дійсних корінь не має. Складаючи рівняння (8) і (9) одержуємо, що дійсних корінь не має. Складаючи рівняння (8) і (9) одержуємо, що  . Тоді . Тоді 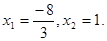 
Відповідь: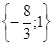 . .
Зауваження. Також рівняння виду 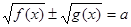 можна вирішувати за допомогою ОПЗ рівняння й рівносильних переходів від одних рівнянь до інших. можна вирішувати за допомогою ОПЗ рівняння й рівносильних переходів від одних рівнянь до інших.
Приклад 3.
Вирішити рівняння 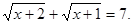
Рішення. Знайдемо ОПЗ змінної х.
ОПЗ: Отже, Отже, 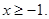
На ОПЗ обидві частини рівняння позитивні, тому після введення у квадрат одержимо рівняння: 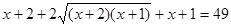 , рівносильне для , рівносильне для 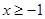 рівнянню рівнянню

Іноді рішення рівняння можна знайти, вирішуючи його на різних числових проміжках.
Для кожного 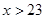 маємо маємо 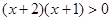 , а , а 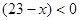 . Отже, серед . Отже, серед 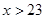 немає рішень рівняння немає рішень рівняння 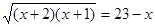 . .
Для 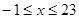 маємо маємо 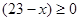 . Отже, . Отже, 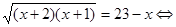 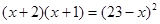 для для 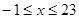 . . 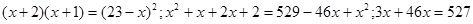 . Тоді . Тоді 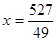 . Так як . Так як 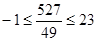 , те , те 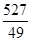 є коренем рівняння є коренем рівняння 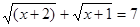 , рівносильному рівнянню , рівносильному рівнянню 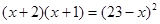 для цих х. для цих х.
Відповідь: 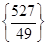 . .
Приклад 4.
Вирішити рівняння 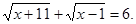
Рішення. Перетворимо вихідне рівняння. 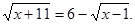
Зведемо обидві частини даного рівняння у квадрат.
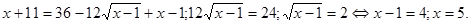
Перевірка показує, що 5 є коренем вихідного рівняння.
Зауваження. Іноді значно простіше можна вирішувати рівняння виду 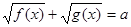 , якщо скористатися властивостями монотонності функцій, а саме тим, що сума двох зростаючих функцій є зростаючою функцією, і всяка монотонна функція кожне своє значення приймає, лише при одному значенні аргументу. Дійсно, функції , якщо скористатися властивостями монотонності функцій, а саме тим, що сума двох зростаючих функцій є зростаючою функцією, і всяка монотонна функція кожне своє значення приймає, лише при одному значенні аргументу. Дійсно, функції 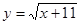 й й 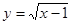 - зростаючі. Отже, їхня сума - зростаюча функція. - зростаючі. Отже, їхня сума - зростаюча функція.
Виходить, вихідне рівняння, якщо має корінь, те тільки один. У цьому випадку, з огляду на, що  , підбором легко знайти, що 5 є коренем вихідного рівняння. , підбором легко знайти, що 5 є коренем вихідного рівняння.
Приклад 5.
Вирішити рівняння 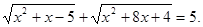
Рішення. Якщо обидві частини вихідного рівняння піднести до квадрата, то вийде досить складне рівняння. Надійдемо по-іншому: перетворимо рівняння до виду:
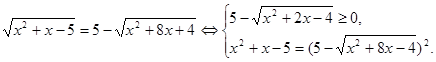
Вирішимо нерівність системи.
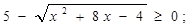 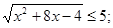 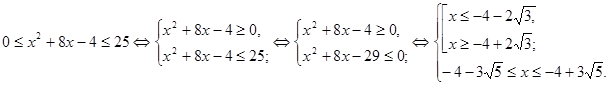
Рішенням системи є множина:
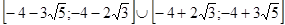 . .
Вирішимо рівняння системи.
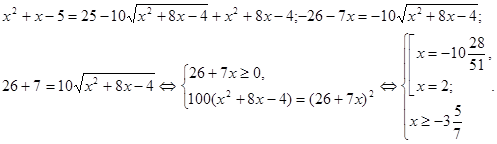
Переконуємося, що 2 належить множині рішень нерівності (мал.1).
Зауваження. Якщо вирішувати дане рівняння введенням обох частин у квадрат, то необхідно виконати перевірку. 2 - ціле число, тому при виконанні перевірки труднощів не виникають. А що стосується значення 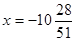 , то підстановка його у вихідне рівняння приводить до досить складних обчислень. Однак такої підстановки можна уникнути, якщо помітити, що при цьому значенні права частина рівняння , то підстановка його у вихідне рівняння приводить до досить складних обчислень. Однак такої підстановки можна уникнути, якщо помітити, що при цьому значенні права частина рівняння 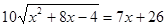 приймає негативне значення: приймає негативне значення: 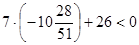 . Тоді як ліва частина рівняння негативної бути не може. Таким чином, . Тоді як ліва частина рівняння негативної бути не може. Таким чином, 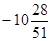 не є коренем рівняння - наслідку даного рівняння. Тим більше, це значення не може бути коренем вихідного рівняння. Отже, корінь рівняння - число 2. не є коренем рівняння - наслідку даного рівняння. Тим більше, це значення не може бути коренем вихідного рівняння. Отже, корінь рівняння - число 2.
Приклад 6.
Вирішити рівняння 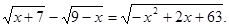
Рішення. Знайдемо ОПЗ змінної х.
ОПЗ: 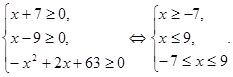
Отже, 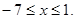
Для будь-яких значень 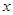 із ОПЗ, що задовольняють умові із ОПЗ, що задовольняють умові 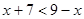 , тобто для , тобто для 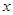 із проміжку із проміжку 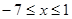 ліва частина рівняння негативна, а перша – ненегативна, виходить, жодне із цих ліва частина рівняння негативна, а перша – ненегативна, виходить, жодне із цих 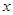 рішенням рівняння бути не може. рішенням рівняння бути не може.
Нехай 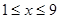 . Для таких . Для таких 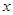 обидві частини рівняння ненегативні, і тому воно рівносильне на цій множині рівнянню: обидві частини рівняння ненегативні, і тому воно рівносильне на цій множині рівнянню:
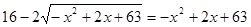 . .
Уведемо нову змінну.  . Одержуємо, що . Одержуємо, що  . Тоді . Тоді 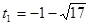 - не задовольняє умові - не задовольняє умові 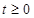 , , 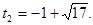 . .
Виконаємо зворотну заміну.
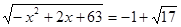 ; ; 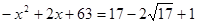 ; ; 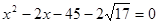
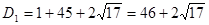 . .
Тоді 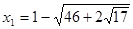 - не задовольняє умові - не задовольняє умові 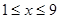 , ,
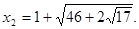
Відповідь: 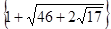 . .
Приклад 7.
Вирішити рівняння 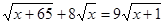
Рішення. Знайдемо ОПЗ змінної х.
ОПЗ: 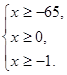
Отже, що 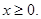
Легко бачити, що 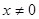 , тому що , тому що 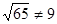 . .
Розділимо обидві частини рівняння на  . Одержуємо, що . Одержуємо, що
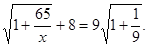
Перетворимо 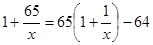 . Уведемо нову змінну. Нехай . Уведемо нову змінну. Нехай 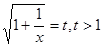 , а , а 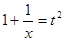 . Тоді рівняння прийме вид: . Тоді рівняння прийме вид: 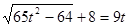 ; ; 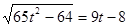 ; ; 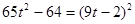 : : 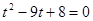 . Тоді . Тоді  - не задовольняє умові - не задовольняє умові 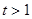 , , 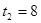 . Виконаємо зворотну заміну. . Виконаємо зворотну заміну.

Відповідь: 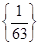 . .
Приклад 8.
Вирішити рівняння 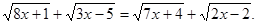
Рішення. Перетворимо вихідне рівняння.
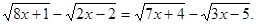
Зведемо обидві частини отриманого рівняння у квадрат.
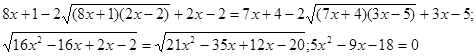
Тоді 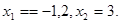
Отже, перевірка показує, що -1,2 - не є коренем вихідного рівняння, а 3 - є.
Зауваження. Дане рівняння можна вирішувати й за допомогою рівносильних переходів, але тоді його рішенні буде набагато складніше, ніж наведене вище.
Відповідь: {3}.
Приклад 9.
Вирішити рівняння 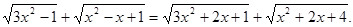
Рішення. Помітимо, що всі квадратні тричлени позитивні відносно 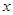 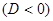 . Перепишемо рівняння у вигляді: . Перепишемо рівняння у вигляді:

Позначимо для стислості підкореневі вираження через 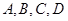 відповідно. Помножимо й розділимо ліву й праву частину рівняння на сполучені співмножники. Одержуємо, що відповідно. Помножимо й розділимо ліву й праву частину рівняння на сполучені співмножники. Одержуємо, що
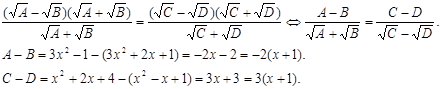
Повернемося до рівняння.
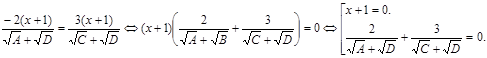
Друге рівняння сукупності рішень не має, оскільки обидва знаменники позитивні. Отже, 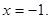
Зауваження. Також рішення даного рівняння можна знайти, досліджуючи його на різних числових проміжках.
Спочатку виділимо 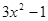 й й 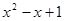 відповідно в кожному з підкореневих виражень у правій частині рівняння. відповідно в кожному з підкореневих виражень у правій частині рівняння.
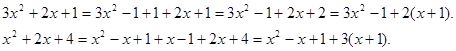
Отже, вихідне рівняння має вигляд:
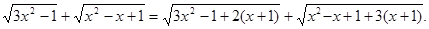
Позначимо для стислості підкореневі вираження через 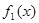 , , 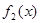 , , 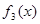 і і 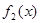 відповідно. Так як вираження відповідно. Так як вираження 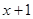 звертається в нуль при звертається в нуль при 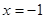 , те розглянемо рішення даного рівняння при , те розглянемо рішення даного рівняння при 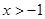 , , 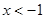 і і 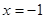 . .
Якщо 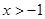 , то , то 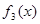 > >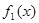 , , 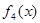 > >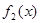 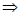 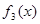 + +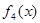 > >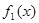 + +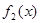 . .
Отже, при 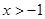 вихідне рівняння не має корінь. вихідне рівняння не має корінь.
Якщо 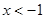 , то , то 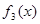 < <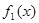 , , 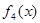 < <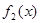 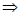 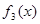 + +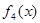 < <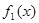 + +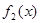 . .
Отже, при 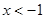 вихідне рівняння не має корінь. вихідне рівняння не має корінь.
Якщо 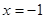 , то , то 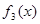 = =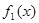 , , 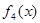 = =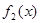 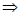 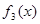 + +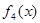 = =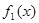 + +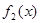 . .
Отже, -1 є єдиним коренем вихідного рівняння.
Відповідь:{-1}.
Зауваження. Отже, при рішенні рівнянь із радикалами потрібне вміти користуватися кожним із цих методів і вибирати в кожному випадку оптимальний.
3. Не стандартні методи рішення ірраціональних рівнянь
Існують ірраціональні рівняння, які вважаються для школярів звичайних освітніх шкіл задачами підвищених труднощів. Для рішення таких рівнянь краще застосовувати не традиційні методи, а прийоми, які не зовсім звичні для учнів. У цій главі приводяться рішення рівнянь заснованих на графічних міркувань, властивостях функції (таких, як монотонність, обмеженість, парність), застосуванні похідній і т.д.
3.1 Застосування основних властивостей функції
3.1.1 Використання області визначення рівняння
Іноді знання області визначення рівняння дозволяє довести, що рівняння не має рішень, а іноді дозволяє знайти рішення рівняння безпосередньою підстановкою чисел з її.
Приклад 1.
Вирішити рівняння  . .
 Рішення. Знайдемо область визначення рівняння. Рішення. Знайдемо область визначення рівняння.
ОПЗ: 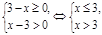 . .
Отже, дана система рішень не має.
Так як система рішень не має, то й дане рівняння не має корінь.
Відповідь:  . .
Приклад 2.
Вирішити рівняння 
Рішення. Знайдемо ОПЗ змінної х.
ОПЗ: 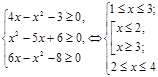 . .
Отже, 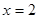 або або 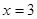 . .
Таким чином, рішення даного рівняння можуть перебувати серед знайдених двох чисел.
Перевіркою переконуємося, що тільки 2 є коренем вихідного рівняння.
Відповідь: {2}.
3.1.2 Використання області значень рівнянь
Приклад 1.
Вирішити рівняння 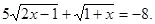
Рішення..  , отже, , отже, 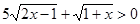 , але , але 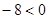 (права частина рівняння негативна, а ліва позитивна), значить дане рівняння не має рішень. (права частина рівняння негативна, а ліва позитивна), значить дане рівняння не має рішень.
Відповідь: 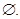
Приклад 2.
Вирішити рівняння 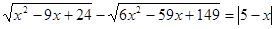 . .
Рішення. 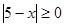 , те , те
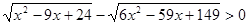 ; ; 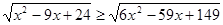 ; ; 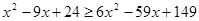 ; ; 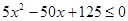 ; ; 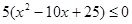 ; ; 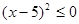 ; ; 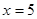 . .
Отже, ліва частина рівняння приймає ненегативне значення тільки при 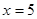 . А це значить, що його коренем може бути тільки значення 5, а може трапитися, що рівняння взагалі не буде мати корінь. Для рішення цього питання виконаємо перевірку. . А це значить, що його коренем може бути тільки значення 5, а може трапитися, що рівняння взагалі не буде мати корінь. Для рішення цього питання виконаємо перевірку.
Перевірка показує, що 5 є коренем вихідного рівняння.
Відповідь: {5}.
3.1.3 Використання монотонності функції
Рішення рівнянь і нерівностей з використанням властивостей монотонності ґрунтується на наступних твердженнях.
1. Нехай f(x) - безперервна й строго монотонна функція на проміжку Q, тоді рівняння f(x)=c, де c - дана константа може мати не більше одного рішення на проміжку Q.
2. Нехай f(x) і g(x) - безперервні на проміжку Q функції, f(x) - строго зростає, а g(x)- строго убуває на цьому проміжку, тоді рівняння f(x)= g(x) може мати не більше одного рішення на проміжку Q.
Відзначимо, що в кожному з випадків проміжки Q можуть мати один з видів: 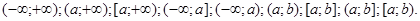
Приклад 1.
Вирішимо рівняння 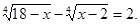
Рішення. Знайдемо ОПЗ змінної х.
ОПЗ: 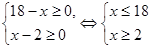 . .
Отже, 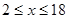 . .
На ОПЗ функції 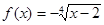 й й 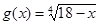 безперервні й строго убувають, отже, безперервна й убуває функція безперервні й строго убувають, отже, безперервна й убуває функція  . Тому кожне своє значення функція h(x) приймає тільки в одній крапці. Так як h(2)=2 , те 2 є єдиним коренем вихідного рівняння. . Тому кожне своє значення функція h(x) приймає тільки в одній крапці. Так як h(2)=2 , те 2 є єдиним коренем вихідного рівняння.
Відповідь: {2}.
3.1.4 Використання обмеженості функції
Якщо при рішенні рівняння 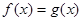 вдається показати, що для всіх вдається показати, що для всіх 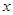 з деякої множини М справедливі нерівності з деякої множини М справедливі нерівності 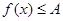 й й 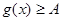 , то на множині М рівняння , то на множині М рівняння 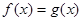 рівносильне системі рівнянь: рівносильне системі рівнянь: 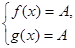 . .
Приклад 1.
Вирішити рівняння 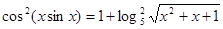 . .
Рішення. Функції, що коштують у різних частинах рівняння, визначені на 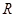 . Для кожного . Для кожного 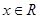 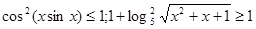 . Отже, дане рівняння рівносильне системі рівнянь . Отже, дане рівняння рівносильне системі рівнянь
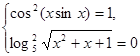 . .
Вирішимо друге рівняння системи:
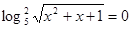 ; ; 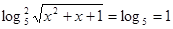 ; ; 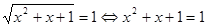
Тоді 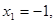 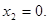
Перевірка показує, що 0 є коренем даного рівняння, а - 1-не є.
Відповідь:{0}.
Приклад 2.
Вирішити рівняння 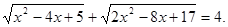
Рішення. Оцінимо підкореневі вираження.
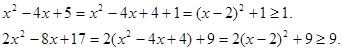
Отже, 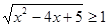 , , 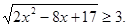
Так як перший доданок лівої частини вихідного рівняння обмежено знизу одиницею, а другий доданок-3, те їхня сума обмежена знизу 4. Тоді ліва частина рівняння стає рівної правої частини рівняння при 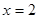 . .
Відповідь:{2}.
3.2 Застосування похідної
У вищенаведених рівняннях були розглянуті застосування деяких властивостей функції, що входять у рівняння. Наприклад, властивості монотонності, обмеженості, існування найбільшого й найменшого значень і т.д. Іноді питання про монотонність, про обмеженість і, особливо, про знаходження найбільшого й найменшого значень функції елементарними методами вимагає трудомістких і тонких досліджень, однак він істотно спрощується при застосуванні похідної. (Наприклад, не завжди можна догадатися, як і яка нерівність застосувати з «класичних»).
Розглянемо застосування похідної при рішенні рівнянь.
3.2.1 Використання монотонності функції
Надалі ми будемо користуватися наступними твердженнями:
1) якщо функція f(x) має позитивну похідну на проміжку М, 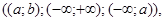 те ця функція зростає на цьому проміжку; те ця функція зростає на цьому проміжку;
2) якщо функція 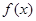 безперервна на проміжку безперервна на проміжку 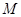  й має усередині проміжку позитивну (негативну) похідну, те ця функції зростає ( убуває) на проміжку; й має усередині проміжку позитивну (негативну) похідну, те ця функції зростає ( убуває) на проміжку;
3) якщо функція 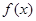 має на інтервалі (а;b) тотожно рівну нулю похідну, те ця функція має на інтервалі (а;b) тотожно рівну нулю похідну, те ця функція 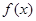 є постійна на цьому інтервалі. є постійна на цьому інтервалі.
Приклад 1.
Вирішити рівняння 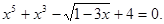
Рішення. Розглянемо функцію 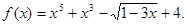
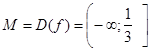 . .
На цьому проміжку 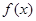 безперервна, усередині його має похідну: безперервна, усередині його має похідну:

Ця похідна позитивна усередині проміжку 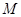 . Тому функція . Тому функція 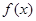 зростає на проміжку М. Отже, вона приймає кожне своє значення в одній крапці. А це означає, що дане рівняння має не більше одного кореня. Легко бачити, що -1 є коренем даного рівняння й по сказаному вище інших корінь не має. зростає на проміжку М. Отже, вона приймає кожне своє значення в одній крапці. А це означає, що дане рівняння має не більше одного кореня. Легко бачити, що -1 є коренем даного рівняння й по сказаному вище інших корінь не має.
Відповідь: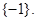
3.2.2 Використання найбільшого й найменшого значень функції
Справедливі наступні твердження:
найбільше (найменше) значення безперервної функції, прийняте на інтервалі 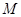 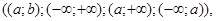 може досягатися в тих крапках інтервалу може досягатися в тих крапках інтервалу 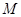 , у яких її похідна дорівнює нулю або не існує (кожна така крапка називається критичною крапкою); , у яких її похідна дорівнює нулю або не існує (кожна така крапка називається критичною крапкою);
щоб знайти найбільше й найменше значення безперервної на відрізку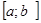 функції, що має на інтервалі (а;b) кінцеве число критичних крапок, досить обчислити значення функції у всіх критичних крапках, що належать інтервалу (а;b), а також у кінцях відрізка й з отриманих чисел вибрати найбільше й найменше; якщо в критичній крапці функції, що має на інтервалі (а;b) кінцеве число критичних крапок, досить обчислити значення функції у всіх критичних крапках, що належать інтервалу (а;b), а також у кінцях відрізка й з отриманих чисел вибрати найбільше й найменше; якщо в критичній крапці 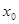 функція безперервна, а її похідна, проходячи через цю крапку, міняє знак з «мінуса» на «плюс», то крапка функція безперервна, а її похідна, проходячи через цю крапку, міняє знак з «мінуса» на «плюс», то крапка 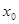 - крапка мінімуму, а якщо її похідна міняє знак з «плюса» на «мінус», те - крапка мінімуму, а якщо її похідна міняє знак з «плюса» на «мінус», те 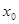 - крапка максимуму. - крапка максимуму.
Приклад 1.
Вирішити рівняння 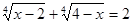 . .
Рішення. Знайдемо ОПЗ змінної x.
ОПЗ: 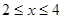 . .
Розглянемо безперервну функцію 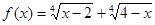 на відрізку [2;4], де D(f)=[2;4]. на відрізку [2;4], де D(f)=[2;4].
Функція f(x) на інтервалі (2;4) має похідну: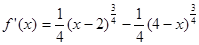 , звертаються в нуль тільки при х=3. , звертаються в нуль тільки при х=3.
Так як функція f(x)безперервна на відрізку [2;4], те її найбільше й найменше значення перебувають серед чисел f(3);f(2);f(4). Так як f(3)=2;f(2)=f(4)=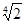 , , 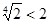 , те найбільше значення f(x) є f(3)=2. , те найбільше значення f(x) є f(3)=2.
Отже, дане рівняння має єдиний корінь: 3.
Відповідь:{3}.
4. Змішані ірраціональні рівняння й методи їхнього рішення
4.1 Ірраціональні рівняння, що містять подвійну ірраціональність
Приклад 1.
Вирішити рівняння 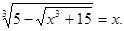
Рішення. Зведемо обидві частини рівняння в куб.
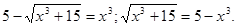 Зведемо обидві частини отриманого рівняння у квадрат. Зведемо обидві частини отриманого рівняння у квадрат. 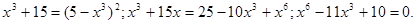
Уведемо нову змінну. Нехай 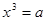 , тоді , тоді 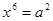 . Одержуємо, що . Одержуємо, що 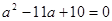 . Тоді . Тоді 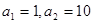 . .
Виконаємо зворотну заміну. 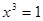 Або Або 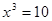 . .
Тоді 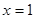 або або 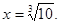
Перевірка показує, що  не є коренем даного рівняння, а 1- є. не є коренем даного рівняння, а 1- є.
Відповідь: {1}.
Приклад 2.
Вирішити рівняння 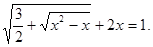
Рішення.
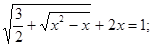 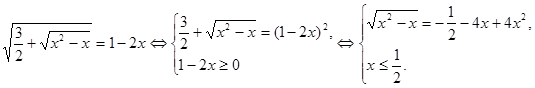
Уведемо нову змінну. Нехай 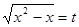 . Тоді . Тоді 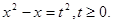
Тоді система прийме наступний вид:
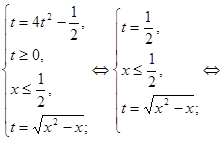
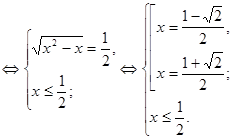
Відповідь: 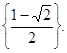
Приклад 3.
Вирішити рівняння 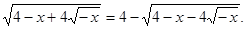
Рішення. Уведемо нову змінну. Нехай 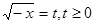 . Тоді . Тоді 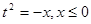 . Одержуємо, що . Одержуємо, що
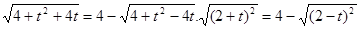 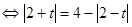 . .
Так як. 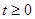 , те дане рівняння рівносильне наступний: , те дане рівняння рівносильне наступний: 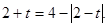
Одержуємо, що 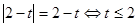 . З огляду на, що . З огляду на, що 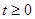 , те рішення: , те рішення:  . Отже, . Отже, 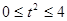 . .
Виконаємо зворотну заміну. 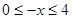 . Тоді . Тоді 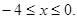
Відповідь: [-4;0].
Приклад 4.
Вирішити рівняння 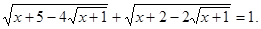
Рішення. Перетворимо підкореневі вираження.
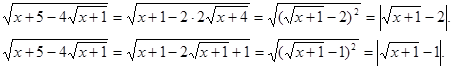
Повернемося до вихідного рівняння.

Останнє рівняння вирішимо методом інтервалів.
Нехай 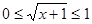 . Одержуємо, що . Одержуємо, що
 . . 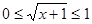 , те на даному проміжку рівняння не має корінь. , те на даному проміжку рівняння не має корінь.
Нехай 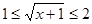 . Одержуємо, що . Одержуємо, що 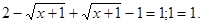 Рівність вірно. Знайдемо всі значення Рівність вірно. Знайдемо всі значення 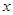 з даного проміжку. з даного проміжку.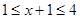 . Отже, . Отже, 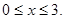
Нехай 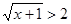 . Одержуємо, що . Одержуємо, що 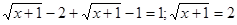 . Так як . Так як 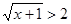 , те на даному проміжку рівняння не має корінь. , те на даному проміжку рівняння не має корінь.
Зауваження. Дане рівняння можна вирішувати, виконавши заміну змінної 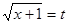 . Після рішення вихідного рівняння щодо змінної . Після рішення вихідного рівняння щодо змінної 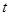 , виконавши зворотну заміну, знайдемо корінь рівняння. , виконавши зворотну заміну, знайдемо корінь рівняння.
Відповідь: [0;3].
Зауваження. Вираження виду 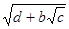 звичайно називають подвійним радикалом або складним радикалом. звичайно називають подвійним радикалом або складним радикалом.
Якщо підкореневе вираження являє собою повний квадрат, то можна в подвійному радикалі звільнитися від зовнішнього радикала, скориставшись рівністю 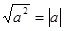 . .
Перетворення подвійних радикалів.
Вправа 1.
Звільнитися від зовнішнього радикала у вираженні 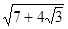 . .
Рішення. Доданок 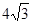 можна розглядати як подвоєний добуток чисел можна розглядати як подвоєний добуток чисел 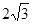 і і 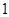 або чисел або чисел 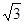 і і 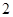 . Число 7 повинне бути дорівнює сумі квадратів цих чисел. Підбором знаходимо, що ця умова виконується для чисел . Число 7 повинне бути дорівнює сумі квадратів цих чисел. Підбором знаходимо, що ця умова виконується для чисел 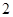 і і 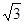 , тобто , тобто 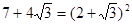 . .
Одержуємо, що
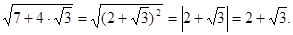
Відповідь: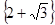 . .
4.2 Ірраціональні показові рівняння
Приклад 1.
Вирішити рівняння 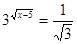 . .
Рішення. 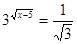 ; ; 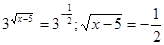 - рішень немає. - рішень немає.
Відповідь: 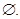
Приклад 2.
Вирішити рівняння 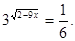
Рішення.
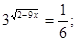 
- Рішень ні, тому що 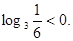
Відповідь: 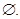
Приклад 3.
Вирішити рівняння 
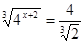 ; ; 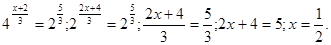
Відповідь: 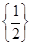 . .
Примі 4.
Вирішити рівняння 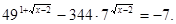
Рішення.
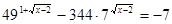 ; ; 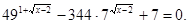
Уведемо нову змінну. Нехай 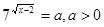 . Одержуємо, що . Одержуємо, що 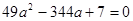 . Тоді . Тоді 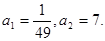
Виконаємо зворотну заміну. 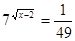 Або Або 
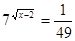 ; ;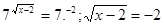
- рішень немає.
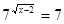 ; ;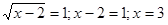 . .
Відповідь:{3}.
Приклад 5.
Вирішити рівняння 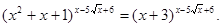
Рішення. Множина М – загальна частина (перетинання) областей існування функцій 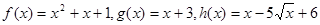 - є всі - є всі 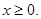
На множині М функції 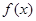 й й 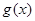 позитивні. Тому, логарифмуючи обидві частини рівняння, одержимо рівняння, рівносильне вихідному на М. позитивні. Тому, логарифмуючи обидві частини рівняння, одержимо рівняння, рівносильне вихідному на М.

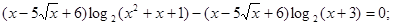
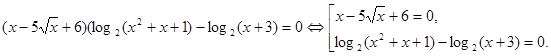
Вирішимо рівняння сукупності.
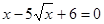 . Уведемо нову змінну. Нехай . Уведемо нову змінну. Нехай 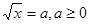 . Одержуємо, що . Одержуємо, що 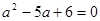 . Тоді . Тоді  . Виконаємо зворотну заміну. . Виконаємо зворотну заміну. 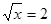 або або  . Тоді . Тоді 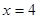 або або 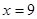 . .
Одержуємо, що вихідне рівняння рівносильне системі:
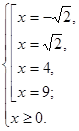
Відповідь: 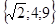 . .
Зауваження. У задачах підвищеної складності зустрічаються рівняння виду 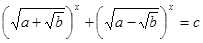 , де , де 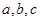 - деякі позитивні числа. Такі рівняння не є ірраціональними рівняннями, тому що не містять змінної під знаком радикала, але всі, же розберемо їхнє рішення в даному пункті. - деякі позитивні числа. Такі рівняння не є ірраціональними рівняннями, тому що не містять змінної під знаком радикала, але всі, же розберемо їхнє рішення в даному пункті.
Приклад 6.
Вирішити рівняння 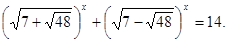
Рішення. Перетворимо вираження 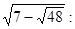
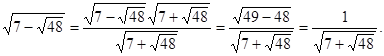
Тоді вихідне рівняння прийме вид: 
Зауваження. Можна помітити, що 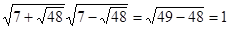 , отже, , отже, 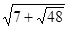 і і 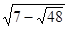 - взаємно обернені числа. Тоді - взаємно обернені числа. Тоді 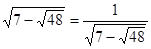 . Уведемо нову змінну. Нехай . Уведемо нову змінну. Нехай 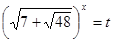 , а , а 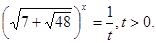 Одержуємо, що вихідне рівняння рівносильне наступний Одержуємо, що вихідне рівняння рівносильне наступний 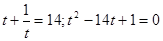 . Тоді . Тоді 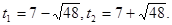
Виконаємо зворотну заміну.
 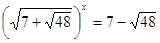 або або 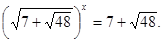
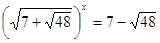 ; ; 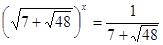 ; ;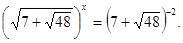
Тоді 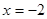 . .
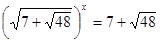 ; ; 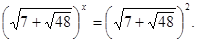
Тоді 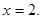
Відповідь :{-2;2}.
4.3 Ірраціональні логарифмічні рівняння
Приклад 1.
Вирішити рівняння 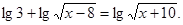
Рішення. 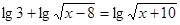 ; ; 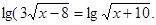
З огляду на, що 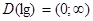 , дане рівняння рівносильне системі: , дане рівняння рівносильне системі:

Відповідь:{32,75}.
Приклад 2.
Вирішити рівняння 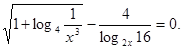
Рішення. 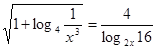 . Перетворимо праву частину рівняння. . Перетворимо праву частину рівняння.
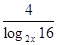 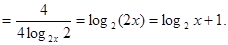
Повернемося до вихідного рівняння.
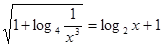 ; ; 
Уведемо нову змінну. Нехай 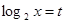 . Одержуємо, що . Одержуємо, що
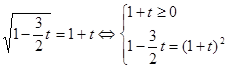 . .
Вирішимо рівняння системи.
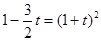 ; ; 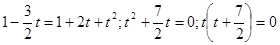 . .
Тоді 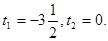
Повернемося до системи: 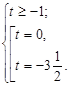 Отже, Отже, 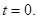
Виконаємо зворотну заміну: 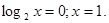
Перевірка показує, що 1 є коренем вихідного рівняння.
Відповідь: {1}.
Приклад 3.
вирішити рівняння 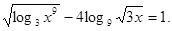
Рішення. Знайдемо ОПЗ змінної х.
ОПЗ: 
 . .
На ОПЗ вихідне рівняння рівносильне рівнянню
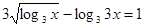 ; ;  ; ; 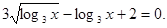
Уведемо нову змінну. Нехай 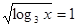 або або 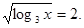
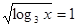 ; ; 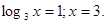
 ; ; 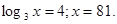
Відповідь: {3;81}.
Висновок
Дана курсова робота допомогла мені навчитися вирішувати ірраціональні рівняння наступних типів: стандартного, нестандартного, показового, логарифмічні, підвищеного рівня. Застосовувати основні властивості функції, область визначення, область значення функції. Використовувати найбільше й найменше значення функції. Застосування похідної. Я вважаю, що цілі які поставлені перед виконанням курсової роботи виконані.
Література
1. Харкова О.В. Ірраціональні рівняння. – К., 2004
2. Колмогоров О.М. Алгебра й початок аналізу. – К., 2003
3. Куланін Е.Д., Норін В.П. 3000 конкурсних задач по математиці. – К., 2000
4. Гусєв В.А., Мордкович А.Д. Довідкові матеріали по математиці. – К., 2003
5. Сканаві М.М. Збірник задач по математиці. – К., 2006
|