СОДЕРЖАНИЕ
Введение
1 Моделирование как метод разработки управленческого решения
1.1 Понятие «модель» и механизм управления проблемами
1.2 Основные концептуальные модели
1.3 Классификация моделей процесса принятия управленческих решений
1.4 Использование моделей процесса принятия решений
2 Разработка и принятие решений в условиях неопределенности и риска
2.1 Цель практической части
2.2 Постановка задачи
2.3 Формализация задачи методами теории игр
2.4 Решение задачи
2.5 Выводы
Заключение
Список используемой литературы
ВВЕДЕНИЕ
В моей курсовой работе, я рассматриваю тему в теоретической части: «Моделирование как метод разработки управленческого решения»
Задачи
, которые я перед собой ставлю:
1. Раскрыть понятие «моделирование».
2. Рассмотреть основные концептуальные модели, с помощью которых описывается принятие управленческих решений в организации.
3. Ознакомиться с классификацией моделей процесса принятия управленческих решений.
4. Рассмотреть, как используются модели процесса принятия управленческих решений.
5. В практической части решить поставленную задачу.
Цель моей курсовой
: Научиться применять знания, полученные на лекциях по данному предмету на практике, а именно принимать решение в условиях неопределенности и риска, с помощью определенных расчетов (часть 2). А также, выяснить для себя, почему моделирование необходимо в процессе принятия управленческого решения.
1 МОДЕЛИРОВАНИЕ, КАК МЕТОД РАЗРАБОТКИ УПРАВЛЕНЧЕСКОГО РЕШЕНИЯ
1.1 Понятие «модель» и механизм управления проблемами
Термин «модель» различными авторами толкуется неодинаково.
Так, скажем, Мексон, Альберт и Хедоури под моделью понимают упрощение реальной жизненной ситуации, к которой она применяется; Шеннон под моделью понимает представление объекта, системы или идеи в некоторой форме, отличной от самой целостности.
Но нам более удачным представляется определение понятия «модель», данное Медоузом и другими в монографии «Пределы роста», в которой анализируются различные возможные сценарии развития, экономики и человечества.
Согласно этому определению, модель – это просто упорядоченный набор предложений о сложной системе.
Модели используются для более четкого понимания того или иного аспекта функционирования объекта путем отбора тех наблюдений, опыта, ощущений и т. д., которые имеют отношение к анализируемой проблеме.
Модель менее сложна, чем моделируемый объект, и позволяет руководителю лучше разобраться в конкретной ситуации и принять правильное решение.
Анализ моделей и особенностей организации как искусственного, так и естественного типа показал, что любая организация, функционирующая в реальном, быстро меняющемся мире, должна обладать эффективно работающим механизмом управления решением возникающих перед ней проблем.
Не менее важен для организации и исполнительный механизм, обеспечивающий реализацию принятого решения.
Механизм управления проблемами организации должен обеспечивать:
· Выявление и диагностику проблем, возникающих в организации при изменении внешних и внутренних условий;
· Соотнесение их со стратегическими и тактическими целями;
· Анализ проблем и подготовку управленческих решений;
· Определение механизма реализации решений;
· Определение Конкретных исполнителей среди существующих структурных подразделений.
Если же среди существующих структурных подразделений организации отсутствуют подразделения, способные эффективно реализовывать принятые решения, а решения являются жизненно важными для выживаемости организации или для достижения стратегических или важных тактических целей, то необходимо создание новых подразделений, способных обеспечить их реализацию.
Примером массового создания новых структурных подразделений на российских предприятиях в период перехода к рынку было создание маркетинговых подразделений, поскольку без обеспечения сбыта производимой предприятием продукции не могло быть и речи о ведении эффективной экономической деятельности.
Модель решения проблем в организации – это, прежде всего, представление ее механизма управления проблемами.
1.2 Основные концептуальные модели
Приведем основные концептуальные модели, с помощью которых описывается управление, а значит, и принятие управленческих решений в организации.
1.Модель «организация-машина». Согласно этой модели, организация представляется, как безличностный механизм, в виде многоуровневой административной иерархии, состоящей из формализованных структур, связей, системы взаимоотношений между ее членами.
Большое внимание при этом уделяется единству командования, функциональному взаимодействию, механизмам управления.
К этой модели близка и «бюрократическая модель» организации.
2.Модель «естественной» организации предполагает, что организации, возникающие естественным образом, развиваются по собственным законам. Они обладают способностью самонастраиваться, реагируя на внешние и внутренние изменения. Отклонение от цели не считается отрицательным результатом, поскольку естественная организация функционирует, как правило, в условиях со значительным элементом неопределенности.
3.Организация-община. В соответствии с этой моделью главным регулятором в организации являются принятые в группе нормы поведения. Особое значение придается межличностным отношениям, отношениям между отдельными членами организации, взаимным привязанностям, общим интересам.
4.Социотехническая модель. Согласно этой модели, особое значение в структуре организации придается влиянию технологического процесса производства на внутригрупповые связи.
5.Интеракционистская модель. В этой модели основное внимание уделяется роли ожиданий и системы ценностей членов организации, их представлениям о ситуации, взаимодействию между членами организации.
6.Институциональная модель. Институциональная модель предполагает, что функционирование и структура организации формируются под воздействием институций – традиций и норм, действующих во внутренней и внешней среде функционирования организации.
7.Конфликтная модель. При использовании конфликтной модели предполагается, что внутри организации сталкиваются и противодействуют друг другу противоположные цели и институции.
Основной задачей при управлении взаимодействием организации с внешней средой является максимальная адаптация организации к внешней среде, снижение неопределенности положения организации, достижение ее стратегических целей.
В зависимости от адаптивности организации к внешней среде различаются два типа управления организацией.
Механический тип:
· консервативная негибкая структура;
· четко определенные, стандартизированные задачи;
· сопротивление изменениям;
· власть проистекает из иерархических уровней в организации;
· иерархическая система контроля;
· командный тип коммуникаций (сверху вниз);
· содержание коммуникаций: принятые руководством решения, приказы распоряжения.
Органический тип:
· гибкая структура;
· динамичные, не жестко определенные задачи;
· готовность к изменениям;
· власть базируется на знаниях и опыте;
· самоконтроль и контроль коллег;
· многонаправленность коммуникаций (вертикальные, горизонтальные, диагональные);
· содержание коммуникаций: информация и советы.
Каждый из типов имеет определенные преимущества и используется в зависимости от того, на сколько динамичны изменения во внешней среде организации.
Непосредственное управление деятельность организации – это процесс взаимосвязанных действий по формированию и использованию ресурсов организации для достижения поставленных перед ней целей.
В этой связи целесообразно также вспомнить концептуальные модели развития человеческого общества в целом.
В частности, органическая модель предполагает, что человеческое общество развивается по законам, близким к законам развития живого организма, в котором каждый орган играет определенную роль, а все органы образуют взаимозависимую структуру.
Согласно этой модели, каждая часть общества выполняет свою функцию, и чем больше они различаются, тем менее они являются взаимозаменимыми.
Процессная модель общества предполагает, что общество развивается как непрерывный процесс соединений и разъединений, слияний и поглощений, определяющих структуру общества.
Поэтому общество не является устойчивым и постоянно подвергается изменениям, адаптируясь к изменениям внутренней и внешней среды.
Неорганическая модель общества предполагает выявление и объединение положительных и отрицательных функций различных частей общества в единое органическое целое.
Более конструктивными представляются целевая и проблемная модели.
Согласно этим моделям, главным направлением деятельности организации является достижение целей, стоящих перед ней, и решение проблем, обеспечивающих, с одной стороны, достижение целей, а с другой – устойчивое развитие и выживание организации.
1.3 Классификации моделей процесса принятия управленческих решений
Дескриптивные и нормативные модели. Дескриптивные модели применяются для описания свойств и параметров процесса принятия решений в целях прогнозирования его хода в будущем.
Успех применения дескриптивных моделей в значительной степени зависит от точности описания законов и закономерностей функционирования объекта управления.
Нормативные модели применяются для управления процессом принятия решений, для формирования его сущностных элементов и его развития.
Нормативные модели предполагают активное участие в процессе принятия решений и его моделировании участников процесса принятия решений.
Индуктивные и дедуктивные модели. Индуктивные модели строятся путем обобщения наблюдений по единичным частным фактам, которые считаются важными для принятия управленческого решения.
Качество индуктивной модели определяется тем, насколько, с одной стороны, удается упростить описание ситуации принятия решения, а с другой – насколько верно удается отразить основные свойства моделируемой ситуации.
При разработке дедуктивных моделей исходят не их анализа конкретных факторов, а из упрощенной системы гипотетических ситуаций.
Здесь путь создания модели – от абстрактного представления управленческой ситуации к ее конкретной реальности.
Проблемно-ориентированные модели и модели решения. Проблемно-ориентированные модели строятся на внедрении новых методов моделирования применительно к конкретной проблемной ситуации принятия решения.
Здесь основная задача состоит в адаптации новых методов для моделирования конкретного управленческого процесса.
Модели решения разрабатываются с учетом возможностей проведения экспериментов с ними, а также возможностей современных управленческих технологий и направлены на решение важнейших управленческих задач.
Алгоритмы, используемые в этих моделях, определяют специфические требования к условиям их применения и структуре моделей.
К числу таких моделей относятся и модели, активно использующие экономико-математические методы решения управленческих задач.
Одноцелевые и многоцелевые модели. Нередко для оценки альтернативного варианта решения необходимо использовать несколько достаточно разнородных, независимых критериев, ориентированных на достижение различных, подчас трудно сопоставимых целей.
Однако решение должно приниматься одно, и наиболее предпочтительный вариант решения должен быть обязательно определен.
Одноцелевыми называются модели, когда имеется одна четко определенная цель, к достижению которой стремиться организация, либо несколько целей, агрегированных в виде одной комплексной цели.
В последнем случае степень достижения цели определяется с помощью специально разрабатываемого комплексного критерия.
Многоцелевыми называются модели, в которых предполагается стремление к достижению нескольких независимых целей, несводимых к одной комплексной.
Существуют методы, позволяющие сопоставлять альтернативные варианты по некоторым критериям и осуществлять их оптимизацию.
В некоторых случаях часть целей (критериев) удается записать в виде ограничений соответствующей экономико-математической модели.
Однопериодные и многопериодные модели. Однопериодные модели исходят из предположения, что сумма оптимальных единичных решений в отдельные периоды принятия решений в целом за весь период принятия решений также дает оптимальное решение. Этот подход не всегда оправдан.
Иногда выигрыш на отдельном этапе может приводить к большим потерям для организации, если рассматривать весь период, на котором принимаются решения.
Многопериодные модели предполагают комплексное решение управленческой проблемы с учетом всего периода принятия управленческого решения.
Однопериодные модели могут использоваться могут использоваться при разработке многопериодной модели с целью более адекватного представления ситуации принятия решения.
Детерминированные и стохастические модели. В детерминированных моделях все факторы, оказывающие влияние на развитие ситуации принятия решения, однозначно определены и их значения известны в момент принятия решения.
Стохастические модели предполагают наличие элемента неопределенности, учитывают возможное вероятностное распределение значений факторов и параметров, определяющих развитие ситуации.
Следует отметить, что детерминированные модели, с одной стороны, являются более упрощенными, поскольку не позволяют достаточно полно учитывать элемент неопределенности. С другой стороны, они позволяют учесть многие дополнительные факторы, зачастую недоступные стохастическим моделям.
Здесь также нередко оказывается справедливой известная закономерность: учитывая одни факторы при моделировании, мы нередко забываем о других. И это естественно. Никакая модель не может учесть абсолютно все факторы.
Но профессионально разработанная модель отличается тем, что позволяет учесть наиболее существенные из них.
1.4 Использование моделей процесса принятия решений
Моделирование собственного процесса принятия решений позволяет сделать существенный шаг в сторону количественных оценок и количественного анализа результатов принимаемых решений.
Это не в коем случае не означает, что принижается роль качественного (неколичественного) анализа результатов принимаемых решений.
Однако создание и использование моделей процесса принятия решений позволяет даже качественно оцениваемые управленческие ситуации оценивать количественно, с помощью специально вводимых вербально-числовых шкал.
Использование моделирования процесса принятия управленческих решений позволяет поднять его на качественно новый уровень, разработать и внедрить в практику принятия управленческих решений современные технологии.
Профессиональное использование моделей процесса принятия решений позволяет менеджеру, с одной стороны, контролировать интуитивные соображения при принятии решений, в частности обеспечивать большую степень непротиворечивости, согласованности и надежности принимаемых управленческих решений, с другой – более полно реализовывать интуицию, опыт и знания.
Однако надо понимать, что модель позволяет найти рациональное решение лишь для того упрощенного варианта ситуации принятия решения, которое используется в модели.
Ни в коем случае нельзя акт принятия решения перекладывать только на заложенные в компьютер модели ситуации и полученные с их помощью альтернативные варианты управленческих решений. Они носят лишь рекомендательный характер и способствуют разработке эффективного управленческого решения. Как говорится, на Бога надейся, а сам не плошай.
В тоже время отказ от их использования в сложных ситуациях, как показывает опыт, снижает эффективность принимаемых управленческих решений.
Решение, найденное с помощью моделирования ситуации принятия решения, нужно обязательно проанализировать сточки зрения полноты учтенных в ней факторов и в случае необходимости внести соответствующие коррективы.
Если в процессе проведения анализа обнаружатся дополнительные факторы, влияющие на развитие ситуации принятия решения, то необходимо соответствующим образом уточнить используемую модель.
Как при разработке модели, так и непосредственно в процессе принятия управленческого решения нельзя недооценивать нередко определяющую роль, которую играет получение и использование экспертной информации.
При принятии особо важных решений могут использоваться независимо несколько моделей, описывающих ситуацию принятия решения с разных сторон.
Окончательное решение принимается на основании сопоставления результатов, полученных с использованием различных моделей ситуации.
На завершающей стадии решающее значение приобретает искусство принятия решения.
Однако не следует забывать, что выдающийся художник, создает свои произведения, опираясь на блестяще отточенную и совершенную технику.
Наибольший эффект при принятии важных управленческих решений дает сочетание опыта, знаний, интуиции менеджера и современных технологий выработки и принятия управленческого решения.
Отметим также, что использование моделей процесса принятия решений позволяет привнести в практику принятия управленческих решений элемент системности, обеспечить эффективное взаимодействие различных этапов принятия решений.
Использование моделей целесообразно при принятии не только особо важных управленческих решений, но и гораздо менее важных решений в часто повторяющихся или многократно возникающих ситуациях принятия решений.
При моделировании процесса принятия решений надо иметь четкое представление о базисных элементах таких моделей, которыми являются:
· ситуация принятия решения,
· время для принятия решения,
· ресурсы, необходимые для реализации решения,
· ресурсы, которыми располагают организация или ЛПР,
· система управляемых факторов,
· система неуправляемых факторов,
· система связей между управляемыми и неуправляемыми факторами,
· альтернативные варианты решений,
· система критериев (оценочная система) для оценки результатов принимаемых решений.
Отметим вот какое важное для современного этапа массированного использования управленческих технологий обстоятельство.
Используемая в процессе принятия управленческого решения модель должна быть адекватна ситуации принятия решения.
Это означает, что модель должна соответствовать:
· структуре и свойствам объекта управления;
· особенностям и возможностям создания используемых методов моделирования и экспериментов, проводимых на базе используемых моделей;
· требованиям решаемой управленческой задачи.
Укрупненно основные этапы формирования требований при разработке адекватных моделей процесса управления представлены на рисунке 4.1.
Рисунок 4.1. Этапы формирования требований при разработке адекватных моделей процесса управления
Отметим, что наряду с требованием соответствия модели объекту управления важную роль играет требование соответствие модели субъекту управления, т. е системе ценностей и предпочтениям ЛПР, уровню владения ЛПР необходимыми профессиональными навыками работы с современными управленческими технологиями, доверия ЛПР к результатам моделирования.
Однако недостаточный анализ ситуации принятия решения нередко приводит к ошибочно принятым управленческим решениям и, следовательно, к дополнительным неоправданным потерям.
Следует отметить также, что один и тот же объект управления может быть представлен с помощью различных моделей в зависимости от того, какого аспекта объекта управления касается принимаемое решение.
Модели процесса управления могут различаться по степени сложности. Например, так называемые мультипликативные факторные модели, характеризующие влияние основных факторов на развитие ситуации принятия решения, являясь достаточно простыми, в то же время вызывают дополнительные сложности при их использовании.
В то же время трудоемкие при разработке экономико-математические модели при их использовании достаточно удобны при наличии современных систем поддержки и сопровождения процесса выработки управленческих решений.
В процессе реального управления организацией менеджер сталкивается с полем проблем, которые должны быть решены в процессе деятельности организации.
Проблемы определяются стратегическими и тактическими целями организации, состоянием внешней и внутренней среды, необходимыми и имеющимися в наличии ресурсами, конкретными значениями неуправляемых и управляемых параметров, ходом самого процесса управления.
В ходе процесса управления вырабатываются альтернативные варианты решений, образующие пространство возможных решений.
Основной задачей управленца является определение для каждой проблемы, принадлежащей возникшему полю проблем, альтернативного варианта решения из пространства решений, позволяющего в наибольшем соответствии с целями организации решить эту проблему.
Для определения наиболее предпочтительного альтернативного варианта решения для конкретной проблемы используются решающие правила, на основании которых осуществляется сравнение и выбор альтернативных вариантов.
Решающие правила позволяют как при одноцелевом, так и при многоцелевом подходе дать однокритериальную или многокритериальную оценку сравниевым вариантам решений.
К числу наиболее распространенных решающих правил можно отнести:
Метод «свертки», при котором рассчитываются значения единого комплексного критерия для каждого альтернативного варианта решения;
Принцип Парето, при котором сопоставляются оценки альтернативных вариантов решения по нескольким критериям и отбрасываются «доминируемые» решения;
Лексикографический выбор, при котором выбор осуществляется сначала по наиболее важным критериям, а затем по менее важным;
Правило максимина, используемое при игровом подходе и реализующее стратегию гарантированного результата, когда выбирается вариант, дающий максимальный эффект при наименее благоприятных действиях противника, и др.
Большое распространение получили решающие правила, основанные на использовании функции полезности альтернативного варианта решения.
2 Разработка и принятие решений в условиях неопределенности и риска
2.1 Цель практической части курсовой работы
Выполнение расчётного задания с применением методов подготовки управленческого решения в условиях неопределенности и риска. Обоснование и выбор одной из альтернатив.
2.2 Постановка задачи
Таблица исходных данных к тестовой задаче
№
варианта
|
Затраты
на НИОКР и внедрение новой
продукции,
млн. руб./ год
|
Эффект
от использования новой
продукции,
млн. руб./ год
|
Затраты
на модернизацию
продукции,
млн. руб./ год
|
Эффект от использования модернизированной продукции, млн. руб. / год |
Априорные
вероятности
«состояний
природы»
|
Условные
вероятности
исходов
эксперимента
|
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 12 |
1,2 |
6 |
0,6 |
1,4 |
0,25;0,50;0,25 |
0,25 0,80 0,20
0,15 0,10 0,70
0,65 0,25 0,15
|
Рассматривается фирма, занимающаяся созданием и эксплуатацией наукоёмкой продукции. Перед руководством фирмы возникла проблема: следует ли принять решение о разработке новой продукции, то есть о проведении научно-исследовательских и опытно-конструкторских работ (НИОКР), или же отказаться от разработки новой продукции в пользу решения о проведении модернизации ранее выпущенной продукции. Ресурсы фирмы ограничены настолько, что заниматься разработкой новой и модернизацией ранее выпущенной продукции одновременно не представляется возможным. Принятие решения осложняется тем, что продолжительность разработки и внедрения новой продукции точно не известна и является дискретной случайной величиной (5, 10 или 15 лет).
Таким образом, решение принимается в условиях неопределённости и связано с риском непроизводительных затрат в рассматриваемом пятнадцатилетнем горизонте планирования.
2.3 Формализация задачи методами теории игр
Расчёты затрат и экономического эффекта (млн. руб.) в зависимости от продолжительности разработки, внедрения и использования новой продукции до конца 15-летнего планового периода удобно представить в виде таблицы возможных ситуаций.
Таблица ситуаций
| Решение планового органа |
Продолжительность разработки,
лет
|
Затраты на НИОКР
и внедрение
|
Эффект
от использования новой продукции
|
Затраты
на модернизацию продукции
|
Эффект от использования модернизированной продукции |
Суммарный эффект |
Прово-
дить
НИОКР
|
5 |
-6 |
60 |
-6 |
14 |
62 |
| 10 |
-12 |
30 |
-3 |
7 |
22 |
| 15 |
-18 |
0 |
0 |
0 |
-18 |
Не про-
водить
НИОКР
|
5 |
0 |
0 |
-9 |
21 |
12 |
| 10 |
0 |
0 |
-9 |
21 |
12 |
| 15 |
0 |
0 |
-9 |
21 |
12 |
Перейдём от неё к «платёжной» матрице игры, которую будем называть матрицей эффектов.
Матрица эффектов
| Решение планово-го органа |
Состояние природы |
| В1 |
В2 |
В3 |
| А1 |
62 |
22 |
-18 |
| А2 |
12 |
12 |
12 |
Где А={А1,А2} – множество решений планирующего органа;
А1 – соответствует решению о проведении НИОКР;
А2 – соответствует решению об отказе от НИОКР;
В={В1,В2,В3} – множество состояний «природы», олицетворяющее неопределенность ситуации,
В1 – проведение НИОКР потребует 5 лет;
В2 – проведение НИОКР потребует 10 лет;
В3 – проведение НИОКР потребует 15 лет.
Рассматриваемая задача решается методами математической теории игр с использованием «платёжной» матрицы (матрицы эффектов либо матрицы потерь) и выбранных критериев принятия решения поэтапно:
– в условиях полной неопределённости;
– в условиях частичной определённости;
– в условиях эксперимента, предшествующего принятию решения;
– с применением аппарата решающих функций и использованием функции риска.
2.4 Решение задачи
Критерии принятия решений в условиях полной неопределённости.
Критерий Уолда
| Решение планового органа |
Минимум выигрыша |
| А1 |
-18 |
| А2 |
12* |
EY = maximinjeij
Максимаксный критерий
| Решение планового органа |
Максимум выигрыша |
| А1 |
62* |
| А2 |
12 |
EM = maximaxjeij
Критерий Гурвича
| Решение планового органа |
Степень оптимизма a |
| 0 |
0,2 |
0,3 |
0,4 |
0,6 |
0,8 |
1 |
0 |
| А1 |
-18 |
-2 |
6 |
14 |
30 |
46 |
62 |
-18 |
| А2 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
Критерий Сэвиджа
| Решение планового органа |
Состояние природы |
Максимум сожаления |
| В1 |
В2 |
В3 |
| А1 |
0 |
0 |
30 |
30 |
| А2 |
50 |
10 |
0 |
50 |
EC = mini maxj (maxi eij - eij)
Критерий Лапласа
Решение
планового органа
|
Равновероятный выигрыш |
| А1 |
22* |
| А2 |
12 |
n
EЛ = maxi S ( eij / n)
j=1
Критерий принятия решений в условиях частичной определённости.
Условия частичной определенности предполагают, что распределение вероятностей состояний «природы» p(bj) известно и статистически устойчиво. В соответствии с исходными данными это распределение имеет вид:
p(b1) =0,25 p(b2) =0,50 p(b3) =0,25
Критерий Байеса-Лапласа
| Решение планового органа |
Математическое ожидание выигрыша |
| А1 |
22* |
| А2 |
12 |

Принятие решений в статистических играх с экспериментом.
Принятию решения предшествует эксперимент. Допустим, что результаты эксперимента образуют множество X = {x1, x2, x3}, где исход эксперимента x1 означает, что проведение данной НИОКР потребует 5 лет, x2 – соответственно 10 лет и x3 – 15 лет. Как правило, такие результаты эксперимента носят не достоверный, а вероятностный характер. Это приводит к необходимости использования условных вероятностей p(xi/bj), которые показывают вероятность прихода к выводу xi, если на самом деле имеет место состояние «природы» bj.
В соответствии с исходными данными условные вероятности p(xi/bj) исходов эксперимента:
p(x1/b1) = 0,25 p(x1/b2) =0,80 p(x1/b3) =0,20
p(x2/b1) = 0,15 (x2/b2) =0,10 p(x2/b3) =0,70
p(x3/b1) =0,65 p(x3/b2) =0,25 p(x3/b3) =0,15
Находим полные вероятности исходов эксперимента:

p(x1) = p(x1/b1)p(b1) + p(x1/b2)p(b2) + p(x1/b3)p(b3)
p(x2) = p(x2/b1)p(b1) + p(x2/b2)p(b2) + p(x2/b3)p(b3)
p(x3) = p(x3/b1)p(b1) + p(x3/b2)p(b2) + p(x3/b3)p(b3)
p(x1) = 0,25×0,25+0,80∙0,50+0,20∙0,25=0,5125
p(x2) = 0,15×0,25+0,10∙0,50+0,70∙0,25=0,2625
p(x3) =0,65×0,25+0,25∙0,50+0,15∙0,25=0,325
Находим апостериорные вероятности состояния природы после того или иного исхода эксперимента (по формуле Байеса):
p(bj / xi) = p(xi / bj) p(bj) / p(xi)
p(b1/x1) = p(x1/b1)p(b1)/p(x1) =0,25∙0,25/0,5125≈0,1220
p(b2/x1) = p(x1/b2)p(b2)/p(x1) = 0,80∙0,50/0,5125≈0,7805
p(b3/x1) = p(x1/b3)p(b3)/p(x1) =0,20∙0,25/0,5125≈0,0976
p(b1/x2) = p(x2/b1)p(b1)/p(x2) =0,15∙0,25/0,2625≈0,1429
p(b2/x2) = p(x2/b2)p(b2)/p(x2) = 0,10∙0,50/0,2625≈0,1905
p(b3/x2) = p(x2/b3)p(b3)/p(x2) =0,70∙0,25/0,2625≈0,6667
p(b1/x3) = p(x3/b1)p(b1)/p(x3) = 0,65∙0,25/0,325=0,5
p(b2/x3) = p(x3/b2)p(b2)/p(x3) = 0,25∙0,50/0,325≈0,3846
p(b3/x3) = p(x3/b3)p(b3)/p(x3) =0,15∙0,25/0,325≈0,1154
Таким образом:
p(b1/x1) = 0,1220 p(b2/x1) = 0,7805 p(b3/x1) = 0,0976
p(b1/x2) = 0,1429 p(b2/x2) = 0,1905 p(b3/x2) = 0,6667
p(b1/x3) = 0,5 p(b2/x3) = 0,3846 p(b3/x3) = 0,1154
Находим по критерию Байеса-Лапласа (с учётом уже апостериорных вероятностей состояний «природы» p(bj / xi) ) ожидаемые выигрыши для каждого исхода эксперимента:

62∙0,1220+22∙0,7805+(-18)∙0,0976=22,97561* Þ А1
EБ (x1) = max
12∙0,1220+12∙0,7805+12∙0,0976=12
62∙0,1429+22∙0,1905+(-18)∙0,6667=1,047619
EБ (x2) = max
12∙0,1429+12∙0,1905+12∙0,6667≈12*Þ А1
62∙0,5+22∙0,3846+(-18)∙0,1154=39,6*Þ А2
EБ (x3) = max
12∙0,5+12∙0,3846+12∙0,1154=12
Средний выигрыш при неизвестном заранее исходе эксперимента равен:

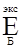 = » 22,97561∙0,5125+12∙0,2625+39,6∙0,3125=27,3 = » 22,97561∙0,5125+12∙0,2625+39,6∙0,3125=27,3
При этом 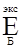 =27,3 > Е = 22 , то есть средний выигрыш с экспериментом больше, чем выигрыш без эксперимента. =27,3 > Е = 22 , то есть средний выигрыш с экспериментом больше, чем выигрыш без эксперимента.
Принятие решений в статистических играх в условиях риска.
В задаче без эксперимента решение (А1 или А2) принимается с использованием априорной информации о состояниях «природы». В задаче с экспериментом плановый орган принимает решение в зависимости от исхода эксперимента (Х1, Х2, Х3). Чтобы формализовать эту задачу, можно заранее проанализировать все возможные исходы эксперимента и составить правило d, определяющее, какое решение следует принять при каждом из возможных исходов эксперимента. Это правило называется решающей функцией.
В рассматриваемом случае (для трёх возможных исходов эксперимента) решающую функцию можно записать в виде
dkls = в (x1, x2, x3) = (Ak, Al, As) ,
где Ak, Al, As – решения, которые следует принять при исходах эксперимента x1, x2, x3 соответственно. Так, решающая функция d112 означает, что соответствие исходов и решений имеет вид
{x1 ®A1 , x2 ®A1 , x3 ®A2 }, то есть при оценке срока НИОКР в 5 или 10 лет принимается решение о разработке новой продукции A1 , а в 15 лет – решение об отказе от разработки новой продукции A2 .
Множество решающих функций состоит из N = mqэлементов, где m - число возможных решений; q – число возможных исходов эксперимента.
В нашем случае m = 2; q = 3; N = mq = 23 = 8 (см. таблицу).
Множество решающих функций
| Результаты эксперимента |
d111 |
d112 |
d121 |
d122 |
d211 |
d212 |
d221 |
d222 |
| X1 |
A1 |
A1 |
A1 |
A1 |
A2 |
A2 |
A2 |
A2 |
| X2 |
A1 |
A1 |
A2 |
A2 |
A1 |
A1 |
A2 |
A2 |
| X3 |
A1 |
A2 |
A1 |
A2 |
A1 |
A2 |
A1 |
A2 |
Из всего множества решающих функций необходимо выбрать такую, которая позволит принимать наиболее выгодные решения. Но для этого надо уметь оценивать сами решающие функции, что может быть сделано при помощи функции риска.
Функцией риска r(bj, dkls) называются средние потери, которые несёт плановый орган при данном состоянии природы и выбранной решающей функции. Число значений функции риска равно N×n, где n – число состояний природы. В нашем случае N = 8, n = 3, тогда 8×3 = 24.
Усреднение потерь ведётся по вероятностям исходов эксперимента при данном состоянии природы. В нашем случае:
r(bj, dkls) = П(bj, Ak)×p(x1/bj) + П(bj, Al)×p(x2/bj) + П(bj, As)×p(x3/bj)
или r(bj, dkls) = Пjk×p(x1/bj) + Пjl×p(x2/bj) + Пjs×p(x3/bj) ,
где Пjk , Пjl , Пjs – элементы матрицы потерь которые получаются из матрицы эффектов путём умножения её элементов на (-1). Отрицательные элементы Пji матрицы потерь означают получение экономического эффекта.
Матрица потерь
| Состояние природы |
Решение планового
органа
|
| А1 |
А2 |
| B1 |
-62 |
-12 |
| B2 |
-22 |
-12 |
| B3 |
18 |
-12 |
Значения функции риска
| Состояние природы |
d111 |
d112 |
d121 |
d122 |
d211 |
D212 |
d221 |
d222 |
| В1 |
-65,1 |
-32,6 |
-57,6 |
-25,1 |
-52,6 |
-20,1 |
-45,1 |
-12,6 |
| В2 |
-25,3 |
-22,8 |
-24,3 |
-21,8 |
-17,3 |
-14,8 |
-16,3 |
-13,8 |
| В3 |
18 |
15 |
-3 |
-6 |
12 |
9 |
-9 |
-12 |
Расчёт значений функции риска
r(b1,d111) = -62∙0.25-62∙0.15-62∙0.65=-65.1
r(b1,d112) = -62∙0.25-62∙0.15-12∙0.65=-32.6
r(b1,d121) = -62∙0.25-12∙0.15-62∙0.65=-57.6
r(b1,d122) = -62∙0.25-12∙0.15-12∙0.65=-25.1
r(b1,d211) = -12∙0.25-62∙0.15-62∙0.65=-52.6
r(b1,d212) = -12∙0.25-62∙0.15-12∙0.65=-20.1
r(b1,d221) = -12∙0.25-12∙0.15-62∙0.65=-45.1
r(b1,d222) = -12∙0.25-12∙0.15-12∙0.65=-12.6
r(b2,d111) =-22∙0.80-22∙0.10-22∙0.25=-25.3
r(b2,d112) =-22∙0.80-22∙0.10-12∙0.25=-22.8
r(b2,d121) =-22∙0.80-12∙0.10-22∙0.25=-24.3
r(b2,d122) =-22∙0.80-12∙0.10-12∙0.25=-21.8
r(b2,d211) =-12∙0.80-22∙0.10-22∙0.25=-17.3
r(b2,d212) =-12∙0.80-22∙0.10-12∙0.25=-14.8
r(b2,d221) =-12∙0.80-12∙0.10-22∙0.25=-16.3
r(b2,d222) =-12∙0.80-12∙0.10-12∙0.25=-13.8
r(b3,d111) = 18∙0.20+18∙0.70+18∙0.15≈18
r(b3,d112) = 18∙0.20+18∙0.70-12∙0.15≈15
r(b3,d121) = 18∙0.20-12∙0.70+18∙0.15≈-3
r(b3,d122) = 18∙0.20-12∙0.70-12∙0.15≈-6
r(b3,d211) =-12∙0.20+18∙0.70+18∙0.15≈12
r(b3,d212) =-12∙0.20+18∙0.70-12∙0.15≈9
r(b3,d221) =-12∙0.20-12∙0.70+18∙0.15≈-9
r(b3,d222) =.-12∙0.20-12∙0.70-12∙0.15≈-12
Наилучшей решающей функцией будет та, которая обеспечивает минимум так называемому байесовскому риску, рассчитываемому по формуле:
r(dkls) = r(b1, dkls)×p(b1) + r(b2, dkls)×p(b2) + r(b3, dkls)×p(b3).
Определим байесовские риски для каждой из решающих функций:
r(d111) = -65.1∙0.25+(-25.3)∙0.5+18∙0.25=-24.425
r(d112) = -32.6∙0.25+(-22.8)∙0.5+15∙0.25=-15.8
r(d121) = -57.6∙0.25+(-24.3)∙0.5+(-3)∙0.25=-27.3
r(d122) =-25.1∙0.25+(-21.8)∙0.5+(-6)∙0.25=-18.675
r(d211) = -52.6∙0.25+(-17.3)∙0.5+12∙0.25=-18.8
r(d212)=-20.1∙0.25+(-14.8)∙0.5+9∙0.25=-10.175
r(d221) =-45.1∙0.25+(-16.3)∙0.5+(-9)∙0.25=-21.675
r(d222) =-12.6∙0.25+(-13.8)∙0.5+(-12)∙0.25=-13.05
Байесовские риски для различных решающих функций
| Решающая функция |
d112 |
d112 |
d121 |
d122 |
d211 |
d212 |
d221 |
d222 |
| Байесовский риск |
-24,425 |
-15,8 |
-27,3 |
-18,675 |
-18,8 |
-10,175 |
-21,675 |
-13,05 |
Умножая полученные байесовские риски на (-1), получим таблицу средних значений эффектов для различных решающих функций
Средние экономические эффекты для различных решающих функций, млн. руб.
| Решающая функция |
d111 |
d112 |
d121 |
d122 |
d211 |
D212 |
d221 |
d222 |
| Средний эффект |
24.425 |
15.8 |
27.3 |
18.675 |
18.8 |
10.175 |
21.675 |
13.05 |
Построим график среднего экономического эффекта в зависимости от выбранной решающей функции. На оси абсцисс графика с равным шагом отмечаются точками решающие функции в той последовательности, в которой они приведены в таблице, а вдоль оси ординат – в выбранном масштабе для каждой решающей функции строятся точки средних значений экономического эффекта.
В результате последовательного соединения найденных точек прямыми линиями получается пилообразный график-диаграмма.2.5 Выводы
В ходе выполнения практической части работы были рассмотрены различные способы и критерии разработки и принятия решений о целесообразности разработки новой продукции в условиях неопределенности.
Минимум байесовского риска (максимум эффекта) достигается при использовании решающей функции d121. Она и является наилучшей. Этот же результат получен и при нахождении среднего выигрыша в п. 4.3. без использования понятий риска и решающей функции, что подтверждает правильность выполненных расчётов.
Наихудшей решающей функцией является d212. При таком абсурдном поведении планового органа величина среднего эффекта ниже, чем даже при полном отказе от разработок новой продукции при любых условиях (пассивное поведение d222).
ЗАКЛЮЧЕНИЕ
В процессе написания моей курсовой, я рассмотрела в теоретической части тему: «Моделирование, как метод разработки управленческого решения».
Материал, подобранный мной, по этой теме помог ответить мне на интересующий меня вопрос: «Для чего в процессе принятия управленческих решений, необходимо моделирование?»
В практической части, в данной задаче, научилась применять знания, полученные на лекциях по данному предмету, на практике, а именно пришла к принятию решения в условиях неопределенности и риска, с помощью определенных расчетов.
На мой взгляд, в моей курсовой все поставленные мною задачи выполнены, основная цель достигнута.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Глущенко В.В. Менеджмент: системные основы. – 2-е изд. – Железнодорожный: ТОО НПЦ «Крылья», 1998. – 224 с.
2. Литвак Б.Г. Разработка управленческого решения: Учебник. – 3-е изд., испр. – М.: Дело, 2002. – 392 с.;
3. Ременников В.Б. Разработка управленческого решения: Учебное пособие для вузов. – М.: ЮНИТИ-ДАНА, 2000. – 140 с.;
4. Смирнов Э.А. Разработка управленческих решений: Учебник для вузов. – М.: ЮНИТИ – ДАНА, 2000. – 271 с.
|