ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Смольный институт свободных искусств и наук
ЭКЗАМЕНАЦИОННАЯ РАБОТА
для аттестации по курсу
Концепции Современного Естествознания
Универсальные законы бедствий и катастроф
ГЕНКИНА Юлия Сергеевна
Преподаватель Куперин Ю.А.
2008
Введение
Учёные часто представляют некоторые события с помощью математических моделей. Когда та или иная модель удовлетворяет не только функции описания
ситуации, но и объяснения
оной, она становится успешной (работоспособной), а когда та же модель сводится к простому алгоритму, способному объяснить разнообразные явления, то модель можно назвать законом
(законом природы). В синергетике (сложных системах) существует некоторое колличество основопологающих теорий. Например, теория бифуркаций, теория катастроф, степенные законы, теория самоорганизованной критичности, законы сохранения. А также она характеризуется такими ключевыми терминами как открытые системы, нелинейность, бифуркационность, эмерджентность, амбивалентность, критичность, самоорганизация и т.д.
Казалось бы, что законы, описывающие бедствия и катастрофы, должны с избытком содержаться в теории катастроф. Но это не так. Теория катастроф лишь описывает сам факт катастроф, дальнейшие сценарии развития событий. Что не является исчерпывающим ответом на вопросы «как» и «почему», интересующие современных учёных. Для ответа на эти вопросы были сформулированы степенные законы распределения.
Итак. О чём же говорит теория катастроф и чем она отличается от универсальных законов бедствий и катастроф? Чем бедствия отличаются от катастроф? И какова область применения всего вышеперечисленного? Изучением этих и других вопросов занимается довольно молодая наука – синергетика. С неё и начнём.
Синергетика (сложные системы)
На мой взгляд, это - универсальная наука, внесшая существенный вклад не только в развитие точных наук, но и в развитие гуманитарных и естественных направлений современности. Эта аномалия произошла потому, что было введено такое понятие как «сложные системы», помогающее просто и кратко описать и объяснить многие закономерности не только в математике, но и в истории, генетике, социологии и прочих «неточных» науках.
Синергетика обнаружила несколько очень важных истин, или точнее - опровергла существующие до неё тезисы. Например, хаос не только разрушителен, но и созидателен. Более того, хаосу скорее присуща вторая черта, чем первая, учитывая ещё один закон природы, приподнесённый нам синергетикой. Этот закон гласит, что развитие - одно из самых созидательных событий во вселенной - осуществляется через неустойчивость, то есть хаотичность. Но это далеко не все открытия этой «универсальной науки». Сложные системы, являющиеся одним из основных предметов изучения синергетики, имеют уникальную структуру, благодаря которой их изучением их занимается отдельная наука. Сложные системы, это системы склонные к катастрофам, но этим их свойства не ограничиваются. Они называются сложными, потому что не подлежат дроблению на более мелкие составляющие, из поведения которых можно сделать вывод о состоянии всей системы. Соответственно, необходимо целостное описание системы, и недопустимо описание через подпроцессы или какие-либо другие составляющие.
Системы могут находиться как в неустойчивом, так и в устойчивом состояниях. В этой работе меня будут интересовать только неустойчивые динамические (системы, состояние которых зависит от времени) системы, так как состояние равновесия – это скорее исключение из правила, нежели правило. В неустойчивых системах присутствует такое явление, как бифуркация. Несмотря на то, что этот термин сначала кажется абсолютно непостижимым чудом лингвистических изысков, оказалось, что это довольно распространённое и универсальное слово, подходящее не только для описания поведения системы. Тем не менее в общих чертах объяснить это довольно просто, особенно если пользоваться образными примерами.
Бифуркация
Бифуркация берёт свои корни от латинского слова bifurcus — раздвоенный применяется для обозначения различных процессов в различных научных сферах. Прелесть сложных систем – их динамическое поведение, постоянное развитие. Чтобы система развивалась, необходим переход из одного состояния в другое. Сам переход называется бифуркацией. Этот термин был введён для обозначения подобного процесса Л.Пуанкаре. Несмотря на широкую область использования данного термина, фактически он описывает один и тот же процесс. При вольном обобщении различных источников получается такое определение: бифуркация – это процесс, когда система двигается в устойчивом состоянии и в какой-то точке её состояние становится неустойчивым, в следствие чего она продолжает развитие не по старой траектории, а по двум новым. Графически это выглядит так.

График показывает, что в процессе развития системы во времени(t), в определённой точке, обозначенной как точка бифуркации, система, вместо одного устойчивого состояния приобретает два новых устойчивых состояния, и далее этот процесс как правило повторяется. Существует масса различных примеров бифуркации: бифуркация рек — разделение русла реки и её долины на две ветви, которые в дальнейшем не сливаются и впадают в различные бассейны; в медицине — разделение трубчатого органа (сосуда или бронха) на 2 ветви одинакового калибра, отходящие в стороны под одинаковыми углами; механическая бифуркация — приобретение нового качества в движениях динамической системы при малом изменении её параметров; разделение старших классов учебного заведения на два отделения; бифуркация времени-пространства (в научной фантастике) — разделение времени на несколько потоков, в каждом из которых происходят свои события. В параллельном времени-пространстве у героев бывают разные жизни.[12]
Пожалуй, пора перейти к классификации бифуркаций, и затем и к теории катастроф.
Бифуркации классифицируются на мягкие
и жёсткие
.
Мягкая бифуркация
– это переход из одного устойчивого состояния в другое, при том что новое устойчивое состояние находится в непосредственной близости от исходного. Т.е. качественно не имеет сильно заметных существенных различий.

Жёсткая бифуркация – это бифуркация, в результате которой система приобретает качественно новое устойчивое состояние, не похожее на исходное. 
Из рисунка видно, что при малом изменении параметра система выбирает новый режим, который уже находится не в непосредственной близости от исходного, следовательно, имеет качественные различия. Именно жёсткие бифуркации легли в основу теории катастроф.
Теория катастроф
Быть может, удастся доказать неизбежность некоторых катастроф, например, болезней или смерти. Познание не обязательно будет обещанием успеха или выживания: оно может вести также к уверенности в нашем поражении, в нашем конце.
РЕНЕ ТОМ
Прежде чем вникнуть в суть теории катастроф, необходимо осознать актуальность данной тематики. Первое, что я считаю нужным отметить – существующие достижения в этой области. Во-первых, философские концепции о всеобщей предопределённости потеряли всякий смысл, что дало надежду на возможность влиять на предполагаемые кардинальные повороты ситуации. Вместе с надеждой появилось осознание ответственности за происходящее, за нарушение баланса в природе, обществе или за отсутствие там гармонии. Остается проблема обеспечения этой информацией максимально большего количества людей, кроме того важен не сам факт получения этой информации людьми, а факт осознания и восприятия этого вывода как побуждения к действиям. К сожалению, это больше похоже на утопию, поэтому продолжая размышлять о пользах теории, нужно не забывать, что и термин «катастрофа» представляет собой не бытовое видение этого события. Катастрофа в данном случае - это просто кардинальное изменение существующей системы. Основной задачей, как мы сейчас уже понимаем, является лишь правильно угадать момент и направление действий. Кроме того, этот факт даёт нам возможность предполагать, что даже и самая безвыходная ситуация – признак надвигающейся «катастрофы», означает лишь перемену, а не Армагедон.
Существует не мало исторических примеров, когда приложенных в нужный момент минимальных усилий хватало для того, чтобы перевернуть всё «с ног на голову». Естественно, что не все попытки «изменить мир» воплотились. Безусловно, это зависит от качества предпринимаемых попыток, но немаловажную роль играет время и место происходящего. Если правильно «угадать момент», то даже с самой бессмысленной идеей можно добиться радикальных изменений, а если нет, то даже самая гениальная мысль не изменит ситуацию. Чтобы уметь определять расстояние системы до точки катастрофы (а именно при переходе через эти точки и происходит самое интересное), нужно потрудиться и найти зависимость системы от внешних параметров в математических моделях, но я сомневаюсь, что кто-то занимался этим на самом деле, скорее это прерогатива будущего.
Как же опознать приближение системы критической точки? Существует такое понятие как «флаги катастроф» - особенности поведения системы, по которым можно это определить. Вот они: наличие нескольких устойчивых состояний, существование неустойчивых состояний, из которых система стремится выйти, возможность скорого изменения системы при незначительных изменениях внешних параметров, необратимость системы
Полагаю, что исчерпывающим примером каждый может назвать сам себя. Очевидно, что человек - это сложная система, равно как и его жизнь. В какие-то моменты индивид оказывается перед выбором, который определит его будущее в какой-то довольно существенной степени (выбор места учёбы, работы, места жительства и т.п.). При этом наблюдается «неуйстойчивое состояние», присущее любому человеческому существу, только в разной степени (вот уже и второй флаг). Как правило, преодолев «первый флаг», постоянно держа второй в руке, человек оказывается лицом к лицу с «третьим флагом», адаптирующего его с его выбором. После принятия решения, как правило, назад пути нет, а это верный признак того, что вы упёрлись в «четвёртый флаг». Если учёный обнаружит один из этих признаков, то ему не составит труда добраться и до остальных. Следует отметить, что это не единственный возможный набор «флагов».
Теория сильно отличается от практики тем, что никаких действий предпринять в случае чего не может. Но она вполне в состоянии понять и объяснить явления, с которыми мы сталкиваемся в реальной жизни. В бытовом смысле катастрофа или хаос это нечто разрушительное, обязательно с летальным исходом, и абсолютно неконтролируемое и необъяснимое. Как утверждает доктор физико-математических наук А.Чуличков: «С точки зрения математики катастрофа и хаос – вовсе не обязательно крушение всех надежд или еще какая-нибудь беда.», и я склонна ему верить. Что же такое «катастрофа» в таком случае? Для разнообразия процитирую другого научного деятеля - В.И.Арнольда: «Катастрофами называются скачкообразные изменения, возникающие в виде внезапного ответа системы на плавное изменение внешних условий». Основная задача теории - это не растеряться в такой ситуации (в преддверии кризиса) и найти тот верный шаг, который поможет не только не испортить ситуацию, но и переманить госпожу удачу на свою сторону. А для того, чтобы вовремя начать придумывать план по захвату удачи, существуют посланники другого мифического субъекта – судьбы. Их мы рассмотрели ранее и выяснили, что называются они «флагами катастроф». Осталось только научиться оперировать этой информацией, и тогда дорога в светлое будущее обеспечена, также как и дружеские отношения с прекрасными госпожами - Судьбой и Удачей.
Как было сказано в начале, теория катастроф дает нам представление о сценариях развития событий после прохождения определенного этапа жизни сложной системы. Зиман, в своём ответе Рене Тому, выделил семь видов катастроф.
Глубже вдаваться в теорию катастроф я не буду, потому что основная цель этой работы -отделить понятия - «бедствие» и «катастрофа». И не просто описать и классифицировать их, а выяснить причину столь многочисленных исследований этой темы, и рассмотреть результаты проделанной работы.
Актуальность и область применения универсальных законов бедствий и катастроф
В последние годы вопрос о развитии научных институтов прогнозирования и мониторинга решается на государственном уровне. В высокоразвитых странах, таких как США, правительство выделяет огромные средства на исследования в этой области. Причина такого серьёзного отношения к подобным событиям очевидна. Это дает возможность прогнозировать катастрофические события в любой области, будь то экономика, политика, метеорология, а также защитить себя от этих явлений. Навряд ли возникнет вопрос: «о каких именно событиях идёт речь?» Но чтобы обозначить масштабы этой тематики, я приведу несколько примеров: крах на фондовой бирже, наводнение, землетрясение, террористические атаки, утечка информации, число заболевших в эпидемии (в т.ч. эпидемии компьютерных вирусов), образование гигантских месторождений минеральных запасов, аварии на нефтеперерабатывающих и нефтетехнических предприятиях и т.п. Среди очевидно негативных событий в этом списке есть и исключение. И хотя я привожу только один пример, это еще не говорит об исключительности события. В любом случае, научные исследования во всех этих областях безусловно являются крайне важными. Несмотря на многочисленные достижения в области исследования катастроф, их количество и ущерб, нанесённый ими в результате не сильно сократился за последние годы. Это происходит потому, что правительства таких стран, как Россия на деле не уделяет этому вопросу достаточного внимания. При хорошо организованной системе исследования катасрофических событий, рост страны во всех отраслях станет очевидным и стабильным.
На протяжении всей истории человечества наука развивается. Эволюционируя, она разрушает многие существенные для своего времени законы, создавая новые теории - ещё более фундаменттальные и приближенные к реальности. Классическая механика и термодинамика лишили человечество мечты изобрести вечный двигатель. Теория относительности уверила нас в том, что не удастся передавать информацию в вакууме со сверхсветовой скоростью. Нелинейная динамика (сложные системы) утверждает наперекор философии, что отнюдь не всё в этом мире предопределено. Более того, существует горизонт предсказаний, дальше которого мы, увы, заглянуть не можем.
Законы распределения вероятностей
Чтобы описать практически все природные явления, как правило, используются функции распределения. Функция распределения это такая функция, которая оперирует числовыми значениями вероятностей. Функции распределения делятся на гауссовые и негауссовые. Гауссовые безошибочно описывают процессы в неживых системах, например, технических. Вообще они имеют настолько широкую область применения, что также называются «нормальными распределениями».
Великий немецкий математик Карл Фридрих Гаусс многие свои фундаментальные открытия сделал в довольно раннем возрасте. Гауссовые распределения, как нетрудно догадаться, как раз одно из его открытий. Для иллюстрации этого закона можно построить гистограмму, показывающую распределение количества людей в Санкт-Петербурге по росту. На оси Х отложить рост, на оси У – количество людей с тем или иным ростом.

Затем проапроксимировав эту гистограмму (грубо говоря, сгладив углы), вы получите график плотности вероятности того, с каким ростом вы встретите человека чаще, а с каким реже. Это и будет закон нормального распределения.
 [10] [10]
Эта огибающая функция в наиболее точной мере может быть задана функцией  . е – это экспонента, т.е. это конкретное число, а следовательно константа. Функция стремительно убывает, что говорит о том, что найти человека с ростом значительно меньше среднего показателя довольно проблематично, а точнее - почти невозможно. Это и называется нормальным распределением. . е – это экспонента, т.е. это конкретное число, а следовательно константа. Функция стремительно убывает, что говорит о том, что найти человека с ростом значительно меньше среднего показателя довольно проблематично, а точнее - почти невозможно. Это и называется нормальным распределением.
Степенные законы
Системы с большим количеством взаимодействующих элементов естественным образом эволюционируют к критическому состоянию, в котором малое событие может привести к катастрофе. Явление самоорганизованной критичности объясняет динамику землетрясений, рынков и экосистем.
ПЕР БАК, КАН ЧЕМ
В июле 1848 года в Париже родился будущий экономист Вильфредо Парето. Получив физико-математическое образование, и занимаясь экономикой, он обнаружил, что распределение вероятностей не ограничивается гауссовым, а в некоторых случаях имеет иной вид, а именно вид степенной функции. Такой вывод он сделал, построив график распределения богатства среди своих сограждан. Как ни странно на графике оказалось не гуассово распределение.

Оказалось, что функция имеет степенной вид f(β)~1/βα
, α≈1. Это произошло потому, что если бы распределение казалось гауссовым, то вероятность найти богатого человека была бы ничтожно мала, что невозможно. Таким образом оказалось, что существуют системы, в которых вариантность возникновения критических событий гораздо больше чем раннее считалось, и этим количеством уже нельзя пренебрегать. С развитием этой теории оказалось, что во многих системах можно найти какие угодно отклонения от усреднённого показателя, и это не редкость. Вскоре это наблюдение было дополнено. Первым делом, исследователи рассмотрели изменение цены на акцию в ограниченный период времени, в полной уверенности, что распределение будет «нормальным». Но, к их удивлению, распределение оказалось степенным, что легко объяснить многочисленными примерами экономических кризисов. На этой почве возникло понятие «тяжёлых хвостов распределения». «Тяжёлыми» они называются, потому что убывают медленнее «хвосты» гауссовых распределений.
Рис.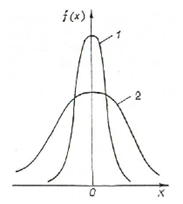
1- Степенное распределение, 2- гауссово распределение.
Графически они выглядят как отклонение от среднего показателя, но в отличае от такого же отклонения в гауссовом распределении, в степенном этими отклонениями пренебрегать нельзя, в них во многом как раз и заключается суть данной теории. Дело в том, что несмотря на редкость событий описываемых в области «тяжёлых хвостов», их масштабами и последствиями пренебрегать нельзя.
Удобнее всего изображать степенную зависимость распределения вероятностей в системе в дважды лографмическом пространстве, т.к. таким образом проще найти α (числовое значение вероятности).
f(β)~1/βα
lnf(β)~ ln 1/βα
lnf(β)~-αlnβ,
это линейная зависимость, при посторении грфика которой, тангенс угла равен значению α. Кроме того, линейную зависимость изобразить проще, чем чертить каждый раз ветвь гиперболы. Вот, например, графическое изображение закона Ципфа. В нём изображена вероятность распределения некоторых слов в английском тексте.
 [11] [11]
(ранг (r) – номер в списке, упрядоченном по убыванию, а в данном случае - по частоте употребления)
Из примеров видно, что степенные законы описывают не только разрушительные события, но и привычные, обыденные вещи.
Тем не менее, при описании критических событий с помощью степенного распределения, опасность явления определяется его показателем (α). Чем меньше α, тем опасней явление. На основе этого разделяют бедствия (где α > 1), и катастрофы (где α < 1). [9]
Универсальные механизмы возникновения и развития катастрофических событий
Катастрофические события, как ранее было сказано, происходят в сложных системах. Теперь я лишь хочу уточнить, что эти системы инвариантны относительно изменений масштаба и состоят из других систем.
Чтобы описать теорию самоорганизованной критичности в общем виде, как правило, используют кучу песка.
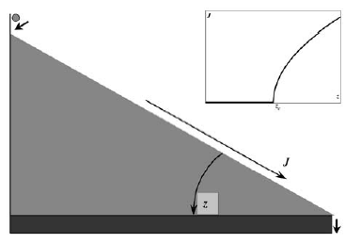 [5] [5]
Допускается тот факт, что песчинки между собой довольно плотно сцеплены, т.е. можно пренебречь незначительной величиной расстояния между песчинками, в то время как величина, которая играет существенную роль для данного эксперимента – угол наклона. Итак, существует некий средний угол наклона z и некоторый критический угол наклона, при котором возникает движение песчинок по куче, т.е. ток песка J. При z никакого движения не происходит, но при процессе Jz стремительно увеличивается. Таким образом, z является управляющим параметром, J – параметром порядка. Кроме того, существует знчение zc
, которое является своеобразной границей между хаотической (z <zc
) и упорядоченной (z > zc
) фазами, и критическая точка (z = zc
), в которой малейшее изменение (а именно - добавление одной песчинки, флуктуация) может привести к катастрофе любого масштаба. Поместить кучу песка в такое «критическое» состояние можно либо самим, посторив такую кучу, либо опытным путём, наблюдая за поведением системы, позволив ей проявить чудеса самоорганизации, подсыпая по одной песчинке на вершину. В первом случае мы отрегулируем управляещий параметр до соответствия равенству z = zc
, во втором случае мы отрегулируем параметр порядка.
Для этого явления, также как для многих, существует модель, позволяющая наглядно проследить за движением и реакцией песчинок, до момента достижения критической точки, во время и после. Эта модель представляет собой двухмерный клеточный автомат, в котором куча представлена в виде двухмерной гексагональной решетки. В ячейках этой решётки находятся единицы и нули, обозначающие локальный наклон поверхности.
 [5] [5]
Единицы и нули говорят об устойчивом положении песчинки: когда локальный наклон превышает единицу, то возникает ток песка, т.е. осыпание. В модели это обозначается тем, что в ячейке стоящее в ней число уменьшается на 2, при этом значения в 2-х ячейках, стоящих ниже, увеличивается на 1. Итак, прибавление одной песчинки в реальной модели будет выглядеть как увеличение значения в верхней ячейке в клеточном автомате. Но увеличением показателя в одной ячейке это не ограничится, потому что по вышеуказанному алгоритму изменяются, как минимум, показатели двух ячеек. Таким образом, в какой-то момент в качестве реакции на добавление одной единицы, возникнет не просто осыпание, а лавина, которая будет продолжаться до обретения системой состояния устойчивости. Когда система обретёт равновесие, процесс релаксации будет считаться законченным. Осыпания происходят сверху вниз, не затрагивая при этом один и тот же слой 2 раза.
Характеристикой лавнины осыпаний является её размер S, т.е. число ячеек, где произошло осыпание. Лавины распределены по размеру степенным образом с показателем, равным 1/3, что подтверждается симуляцией модели, результаты которой приведены на рисунке ниже.
 [8] [8]
Линейная часть графика соответствует степенному распределению с = 1/3. Отклонение от масштабно инвариантного поведения при больших S
связано с конечностью размеров системы. Развитие очень больших лавин обрывается из-за достижения ими нижнего края решетки, что обуславливает горб в правой части графика. Такие события можно трактовать как сверхкатастрофы – порождающая их система оказывается мала для нормального завершения этих лавин.[8]
«Масштабно инвариантное распределение означает склонность системы к катастрофам. Её отклик на элементарное воздействие не имеет собственного характерного размера, и поэтому в ней возможны гигантские события без отчётливых причин. И хотя для каждой лавины можно указать ту самую песчинку, которая её спровоцировала, корни катастроф лежат, конечно же, не в песчинках, а в критических свойствах системы, где малые причины могут вызывать большие следствия.»[5]
Прогнозирование катастрофических событий
Из примера с кучей песка, стало очевидным, что катастрофическое событие не происходит внезапно, ему предшествуют менее значительные события. Прогнозирование катастрофических событий ведётся практически во всех областях современной науки.
Оценка вероятностей аварий на нефтеперерабатывающих, нефтехимических и химических предприятиях. [9]

В таблице представлено число пострадавших в 36-ти авариях в этой области за период 1974-2005 годы.
Из-за «тяжёлого хвоста распределения», среднее значение числа пострадавших не содержит полезной информации. А вот график распределения вероятностей в дважды логарифмическом пространстве даёт нам весьма ценную информацию.
 [9] [9]
В данном случае α=0,4872.
Благодаря этому можно сказать, что авария с ущербом 2,1 млн. пострадавших повторяется в среднем раз в 255 лет. К сожалению, на данный момент нет возможности учесть будущее развитие промышленности в этой отрасли, чтобы стало возможным получить более точную информацию, тем не менее всегда есть возможность снова произвести расчеты, руководствуясь новыми показателями.
Перейдём к природным катастрофам. Их разрушительность сравнима с потерями при военных действиях, но они более внезапны и не оставляют возможности «дать сдачи». Как было показано выше, несмотря на общепринятое мнение, благодаря набору опреденённых знаний, навыков и имея доступ к необходимой информации, становится возможным довольно точно спрогнозировать надвигающуюся катастрофу. Благодаря своевременому прогнозу возможно нивелировать последствия стихийных бедствий. Безусловно, в таком случае не последнюю роль играет планирование реакционных действий. В совокупности, действия по прогнозу катастрофических событий и их ликвидации или сглаживании, называются управлением рисками. При этом немаловажным фактором является вычесление степени риска, что делается посредством использования рассмотренных выше степенных законов. Таким образом, риск характеризуется как частота и последствия того или иного бедствия, а благодаря степенным законам и то и другое можно вычислить. Другое дело – кто будет этим заниматься, кто профинансирует и обеспечит всем необходимым специалистов, готовых изучать и прогнозировать. Пример эффективного использования возможностей современной науки можно найти в ближайшем зарубежье.
Риск природных катастроф является частым и одним из наиболее опасных явлений в современном мире. На нашей планете существует место под названием Ферганская долина. Этот участок на поверхности земли характеризуется как межгорная котловина. Район в котором она расположена является повышенно сейсмичным, кроме того площадь долины находится на территории трёх разных государств: Таджикистана, Узбекистана и Кыргызстана. Кроме того, плотность населения в этом районе довольно велика: 900, 360 и 500 человек на 1км2
. На этой территории довольно часто проявляются те или иные стихийные бедствия. Существует предрасположенность данного участка к возникновению крупномасштабных природных катастроф, что может нанести существенный урон государствам. Наиболее опасными считаются оползни и сели, а также наводнения.
Именно этот участок суши был подвергнут исследованиям учёных. Со временем возникла возможность составлять прогноз активизации оползней. Это произошло благодаря применению свойств степенных законов, о которых неоднократно говорилось выше. Для получения подобных результатов потребовался анализ многолетнего цикла изменения основных факторов, влияющих на систему. Например, оползни. Оползни возникают при нарушении устойчивости склона в момент, когда сила связанности грунтов оползневого склона или горных пород оказывается меньше силы тяжести. При определённых условиях, таких как малоустойчивое состояние склона, решающей «песчинкой» может послужить небольшое землетрясение, выпас скота, неправильная стратегия применения противооползневых методов и т.п. Для получения максимально точного прогноза, необходимо объединить усилия специалистам на разных уровнях управления рисками. Безусловно, регулярный наносимый ущерб, возникающий вследствие стихийных бедствий, может быть снижет, за счёт создания центра по прогнозированию катастроф. К сожалению, на сегодняшний день в Ферганской долине не существует ни одной системы по управлению рисками, что существенно сказывается на экономике стран, на долю которых приходится та или иная часть территории это долины. Как только начнутся крупно-масштабные стихийные бедствия в данном регионе, попытки снизить ущерб будут локальными и безрезультатными, по причинам низкой организации спасательных служб трёх стран, и почти отсутствующей связи между службами этих стран. Таким образом, Ферганская долина и её жители, вследствие низкого уровня экономического развития, природных факторов, низкого уровня взаимодействия служб спасения, и отсутствия центра прогнозирования и исследований, находятся в довольно плачевной ситуации, выход из которой заключается в объединении сил трёх стран, для создания единой системы управления риском, и в том числе финансово-политическими отношениями, возникающими в процессе этого управления.
Заключение
При рассмотрении небольшого участка суши, принадлежащему трём разным странам, был выявлена серьёзная проблема, грозящая существенным уроном всем сферам этих государств. Что уж говорить об актуальности данной темы в рамках более глобальных и развитых систем, таких как международные рынки, курсы валют и прочее. Возможность прогнозирования их поведения даёт уникальные возможности, описанные во многих фантастических книгах, возможности сопоставимые с миссией спасения человечества.
Многочисленные примеры экономических кризисов, природных катастроф, социальных и политических реформ, поддаются математическому описанию и прогнозированию. Современная наука устремилась в будущее, уверенно преодолевая возникающие препятствия. На данный момент существует всё необходимое, чтобы во всеоружии направляться навстречу трудностям. Остается проблема финансирования и организации соответствующих научных центров. К сожалению, в России специалисты по управлению рисками не имеют возможности работать в соответствующем направлении, что приводит к возрастающим потерям и ущербу вследствие бедствий и катастроф.
Литература
1. Малинецкий Г.Г. Управление Риском. Глава XСамоорганизованная критичность, как универсальный механизм катастроф. http://www.keldysh.ru/papers/2003/source/book/gmalin/gl10.htm
2. Малинецкий Г.Г. Управление Риском. Глава V статистика катастрофических событий. http://www.keldysh.ru/papers/2003/source/book/gmalin/gl5.htm
3. А.Чуличков. Теория катастроф и развитие мира. http://katastrofa.h12.ru/theory.htm
4. Самоорганизованная критичность. http://katastrofa.h12.ru/krit.htm
5. А.В.Подлазов. Теория самоорганизованной критичности – наука о сложности. http://theorphys.mipt.ru/mezhpr/mezhpred2/podlazov.pdf
6. За горизонтом предсказуемости. http://n-t.ru/tp/mr/zgp.htm
7. Зиман. Теория катастроф. http://www.omegafield.net/library/dynamical/zeeman-catastrophe_theory.pdf
8. Г.Г.Малинецкий, А.В.Подлазов, И.В.Кузнецов. О национальной системе научного мониторинга. http://www.keldysh.ru/papers/2004/prep47/prep2004_47.html
9. Д.В. Токарев. Оценка вероятностей аварий на нефтеперерабатывающих, нефтехимических и химических предприятиях. http://www.ogbus.ru/authors/Tokarev/Tokarev_2.pdf
10. Изучения закона распределения нормальных величин. http://kfmirea.ru/upload/lab_1-71.pdf
11. Шредер. Фракталы, Хаос, Степенные законы.
12. Энциклопедический фонд России. Бифуркация. http://www.russika.ru/termin.asp?ter=3496
|