| Современные радиолокаторы можно условно разделить условно на два класса: радиолокаторы в которых используются видеоимпульсные сигналы и радиолокаторы с использованием гармонических модулированных или немодулированных сигналов. Характерной особенностью радиолокаторов второго типа является возможность получать изображения малозаглубленных предметов непосредственно, без какой либо последующей обработки [1]. Изображения получаются методом сканирования приемо-передающим антенным блоком по поверхности раздела двух сред. Получаемые таким образом изображения формируются в соответствии с принципом формирования голограммы [1,2] поскольку в формировании получаемого изображения участвуют два сигнала – опорный и предметный. Опорный сигнал получается в результате неизбежной электродинамической связи между передающей и приемной антенной, расположенных в одном антенном блоке, как это имеет место в радиолокаторе типа «Раскан» [1], либо подмешиванием опорного сигнала из задающего генератора в приемник на основной или промежуточной частотах. Предметный сигнал получается в результате отражения от объектов, находящихся под поверхностью. Опорный сигнал является аналогом опорной волны при записи оптических голограмм, а сигнал, отраженный от заглубленных предметов, является аналогом предметной волны, отраженной от голографируемого объекта.
Для восстановления изображения заглубленного предмета, которым считается представление о геометрическом расположении интерферирующих источников, дающих интерференционную картину в виде голограммы, исследователями предлагаются перечисляемые ниже методы.
В работе [1] предлагается метод, основанный на восстановлении голограммы методом апертурного синтеза. Данный метод основан на известном принципе обработки данных радиолокаторов с синтезированием апертуры, когда мера отражательных характеристик данной точки зондируемого объекта получается в результате свертки принимаемого сигнала с ожидаемым опорным сигналом из этой же точки [3]. Непосредственное применение данного метода к подповерхностной радиолокации наталкивается на трудности, связанные с тем, что амплитуда опорного сигнала зависит от дальности, на которой восстанавливается изображение, приводя к тому, что результирующая свертка может иметь большее по модулю значение для меньшей опорной дальности, чем действительная дальность до зондируемого предмета. Для преодоления этого недостатка в работе [1] используется нормировка используемого опорного сигнала по энергии. Отсутствие априорной информации об изменении фазы при отражении от заглубленного предмета приводит к ошибкам данного метода, которые выражаются в том, что глубина фокусировки изображения зависит от задаваемой фазы для опорного сигнала.
В работе [4] для восстановления изображений подповерхностного зондирования предлагается метод миграции. В этом методе изображение точечного рассеивателя получается в результате вычисления корреляции распространяемого обратно в среду рассеянного поля и поля, распространяющегося в среду непосредственно от излучателя, возбуждающего электромагнитные волны. В данном методе рассматривается ЛЧМ зондирующий сигнал и для рассматриваемого типа радиолокаторов непосредственно неприменим.
Ряд работ посвящен решению обратной задачи с использованием линеаризации интегрального уравнения Липпмана-Швингера [5,6]. В работе [5] для восстановления изображения предметов, скрытых под одеждой человека, по результатам радиолокационных данных голографического типа с использованием многочастотного сигнала предлагается метод, основанный на линеаризации интегрального уравнения Липпмана-Швингера с использованием приближения слабого рассеяния (приближение Борна). Данный метод обладает значительной вычислительной трудностью, хотя и допускает возможность дальнейшей оптимизации вычислений с использованием специализированных сигнальных процессоров и предварительным вычислением интерполяционных матриц.
Ряд исследований посвящен разработке методов, которые основаны на так называемом алгоритме обращения времени [7,8], смысл которых заключается в том, что принимаемый сигнал, распространяемый обратно в среду, фокусируется вблизи места расположения предмета. В работе [7] для фокусировки по дальности используются когерентная компонента сигнала с линейной частотной модуляцией, а для фокусировки изображения в перпендикулярной плоскости используются статистические моменты высших порядков. Особенностью такого метода является наблюдаемый эффект сверхразрешения (super resolution), который заключается в том, что наличие укрывающей среды с многократным рассеянием приводит к лучшей фокусировке изображения, чем в условиях, когда зондирование осуществляется в свободном пространстве.
Для сканирующего радиолокатора типа «Раскан», использующего немодулированные гармонические сигналы на нескольких частотах, желательно разработать метод, способный работать в реальном режиме времени, для оперативной классификации изображений оператором. При этом желательно, чтобы аппаратная модификация самого радиолокатора была незначительной. Существующие методы восстановления изображений не могут непосредственно использоваться для решения этой задачи в виду их значительной вычислительной трудности, либо из-за того, что потребуют существенной модификации радиолокатора.
Для решения этой проблемы в статье рассмотрен метод построения изображений по данным подповерхностного голографического зондирования с использованием метода обращения волнового фронта, который существует для восстановления оптических голограмм [9]. Описание данного метода с использованием оптических методов обработки информации приводится в работе [2]. Существующий на сегодня уровень развития вычислительной техники позволяет проделать процедуру восстановления голограммы численно без привлечения оптического метода обработки информации, который заключался бы в изготовлении оптического транспаранта по данным радиоголографического зондирования и последующего восстановления оптической голограммы с использованием когерентных источников излучения оптического диапазона. Численная реализация данного метода с использованием спектрального метода может решить данную задачу в реальном масштабе времени, поскольку такая обработка сигнала допускает быструю реализацию метода с использованием быстрого алгоритма преобразования Фурье. Таким образом, задачами данной статьи являются разработка модели регистрируемого радиолокатором сигнала и метода восстановления изображения заглубленного предмета по регистрируемым на поверхности раздела сигналам.
Комплексная амплитуда поля апертурной антенны, создаваемая в нижнем полупространстве, характеризуемом комплексной диэлектрической проницаемостью
Рассмотрим апертуру антенны находящейся над полупространством 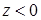 , заполненным веществом, имеющим комплексную диэлектрическую проницаемость , заполненным веществом, имеющим комплексную диэлектрическую проницаемость  , как показано на рис. 1. Антенна располагается так, что координаты центра ее апертуры в системе координат , как показано на рис. 1. Антенна располагается так, что координаты центра ее апертуры в системе координат  равны равны  . Система координат, связанная с центром апертуры и лежащая в плоскости . Система координат, связанная с центром апертуры и лежащая в плоскости  , обозначена как , обозначена как  . Найдем комплексную амплитуду поля, создаваемую излучающей антенной в точке . Найдем комплексную амплитуду поля, создаваемую излучающей антенной в точке  , лежащей в нижнем полупространстве. , лежащей в нижнем полупространстве.
Пусть  распределение комплексной амплитуды поля на апертуре антенны в декартовой системе координат с началом в центре апертуры. Тогда спектр плоских волн распределения комплексной амплитуды по апертуре антенны в системе координат распределение комплексной амплитуды поля на апертуре антенны в декартовой системе координат с началом в центре апертуры. Тогда спектр плоских волн распределения комплексной амплитуды по апертуре антенны в системе координат  будет будет
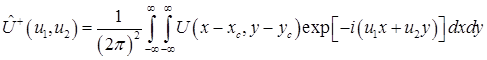 . .
Знак «+» в обозначении спектра плоских волн означает, что спектр задан в плоскости  . Оговорим сразу, что для прямого и обратного преобразования Фурье будем использовать пару . Оговорим сразу, что для прямого и обратного преобразования Фурье будем использовать пару
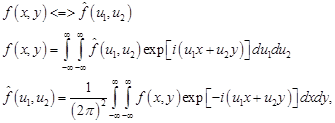
где третье выражение будем называть преобразованием Фурье, а второе – обратным преобразованием.
Каждая плоская волна, распространяющаяся в направлении, задаваемом парой 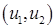 и имеющая комплексную амплитуду и имеющая комплексную амплитуду  согласно (1) после прохождения плоскости согласно (1) после прохождения плоскости  трансформируется следующим образом трансформируется следующим образом
 , (3) , (3)
где 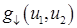 – френелевский коэффициент прохождения плоской волны, характеризуемой парой – френелевский коэффициент прохождения плоской волны, характеризуемой парой 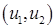 , при распространении вниз. , при распространении вниз.
Решая уравнение Гельмгольца для однородного пространства, характеризуемого волновым числом 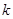 , которое в общем случае может быть комплексным, можно получить соотношение, связывающее спектры плоских волн в параллельных плоскостях. Соответствующее соотношение в обозначениях рис. 1 будет иметь вид , которое в общем случае может быть комплексным, можно получить соотношение, связывающее спектры плоских волн в параллельных плоскостях. Соответствующее соотношение в обозначениях рис. 1 будет иметь вид
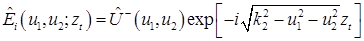 . (4) . (4)
Зная спектр плоских волн в произвольной плоскости  , можно вычислить соответствующую комплексную амплитуду поля с помощью преобразования Фурье , можно вычислить соответствующую комплексную амплитуду поля с помощью преобразования Фурье
 .(5) .(5)
Делая замену переменных 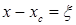 , ,  в выражении (1) получаем в выражении (1) получаем
 ,(6) ,(6)
в котором
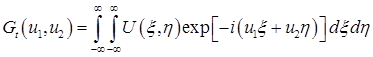 (7) (7)
– преобразование Фурье от распределения комплексной амплитуды по апертуре излучающей антенны.
Подставляя (1), (3) и (4) в выражение (5), получим
 (8) (8)
Выражение (8) позволяет по известному распределению комплексной амплитуды по апертуре излучающей антенны находить комплексную амплитуду в нижнем полупространстве, заполненном однородным веществом, имеющим комплексную диэлектрическую проницаемость  . .
Комплексная амплитуда поля точечного излучателя, находящегося в нижнем полупространстве, принимаемая антенной
Рассмотрим точечный отражатель, расположенный в нижнем полупространстве и имеющий координаты  . Будем отраженное от него поле в плоскости . Будем отраженное от него поле в плоскости  описывать функцией описывать функцией
 ,(9) ,(9)
где 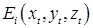 задается выражением (8). задается выражением (8).
Спектр плоских волн для распределения комплексной амплитуды (9), вычисленный с использованием (2) будет иметь вид
 .(10) .(10)
Распространяясь до плоскости  , спектр трансформируется согласно , спектр трансформируется согласно
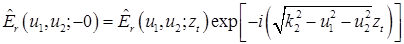 .(11) .(11)
После прохождения границы раздела, каждая плоская волна должна быть умножена на коэффициент прохождения Френеля при распространении снизу вверх, таким образом, что спектр плоских волн в плоскости 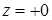 принимает вид принимает вид
 ,(12) ,(12)
где  – коэффициент прохождения Френеля для плоской волны, характеризуемой парой – коэффициент прохождения Френеля для плоской волны, характеризуемой парой  . .
Распределение комплексной амплитуды поля в плоскости  будет находиться как обратное преобразование Фурье от спектра, задаваемого выражением (12) будет находиться как обратное преобразование Фурье от спектра, задаваемого выражением (12)
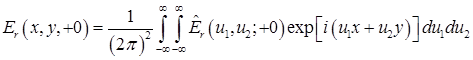 .(13) .(13)
Принимаемый апертурой антенны, центр которой имеет координаты  , сигнал записывается как , сигнал записывается как
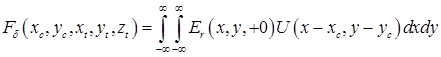 .(14) .(14)
Подстановка (13) в (14) приводит к такому выражению для комплексного выхода с антенны
 (15) (15)
в котором
 (16) (16)
– обратное преобразование Фурье от распределения комплексной амплитуды по апертуре антенны.
Комплексный выход 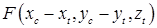 с антенны радиолокатора, центр апертуры которой имеет координаты с антенны радиолокатора, центр апертуры которой имеет координаты  , при отражении от точечного рассеивателя, координаты которого задаются вектором , при отражении от точечного рассеивателя, координаты которого задаются вектором  , может быть записан следующим образом , может быть записан следующим образом
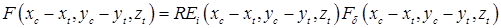 ,(17) ,(17)
где  – комплексный коэффициент отражения от элементарной площадки заглубленного предмета. – комплексный коэффициент отражения от элементарной площадки заглубленного предмета.
Сигнал, отраженный от поверхности и регистрируемый приемником
Найдем регистрируемый приемником сигнал, который получается в результате отражения от поверхности раздела. Для этого сначала запишем выражение для спектра плоских волн после отражения от поверхности раздела, которое будет произведением (1) и коэффициента отражения Френеля 
 . (18) . (18)
Спектру (18) соответствует связанное с ним обратным преобразованием Фурье распределение комплексной амплитуды поля
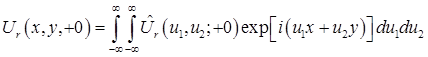 (19) (19)
Комплексный выход антенны будет найден интегрированием (19) по апертуре антенны
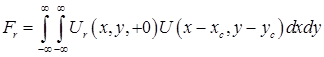 .(20) .(20)
Выполняя подстановку (18) и (19) в (20), осуществляя интегрирование, получается следующее выражение для комплексного выхода антенны, обусловленного отражением от поверхности раздела
 .(21) .(21)
В полученном выражении комплексное число  , как и следовало ожидать, не зависит от координат центра апертуры. Величина , как и следовало ожидать, не зависит от координат центра апертуры. Величина 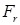 зависит от комплексной диэлектрической проницаемости нижнего полупространства через коэффициент отражения Френеля и является постоянным слагаемым, которое, наряду с опорным сигналом от передатчика к приемнику, добавляется к сигналу, регистрируемому радиолокатором после отражения от рассеивателей, находящихся в нижнем полупространстве. зависит от комплексной диэлектрической проницаемости нижнего полупространства через коэффициент отражения Френеля и является постоянным слагаемым, которое, наряду с опорным сигналом от передатчика к приемнику, добавляется к сигналу, регистрируемому радиолокатором после отражения от рассеивателей, находящихся в нижнем полупространстве.
Коэффициенты прохождения и отражения Френеля для плоской волны
Найдем коэффициенты Френеля для отражения и прохождения плоской волны, задаваемой уравнением
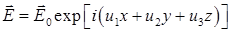 , (22) , (22)
в котором величины 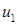 , ,  и и  в общем случае могут быть комплексными и не иметь смысла проекций волнового вектора в общем случае могут быть комплексными и не иметь смысла проекций волнового вектора  на оси координат. В таком случае уравнение (22) будет описывать как однородную, так и неоднородную волну, в которой направление убывания амплитуды и направление распространения могут не совпадать [10]. Подстановка (22) в уравнение Гельмгольца, записанного для однородной среды вне области, занятой источниками на оси координат. В таком случае уравнение (22) будет описывать как однородную, так и неоднородную волну, в которой направление убывания амплитуды и направление распространения могут не совпадать [10]. Подстановка (22) в уравнение Гельмгольца, записанного для однородной среды вне области, занятой источниками
 , (23) , (23)
в котором
 , (24) , (24)
позволяет получить условие, которое должно выполняться для величин 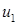 , ,  и и  в общем случае в общем случае
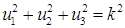 . (25) . (25)
В предыдущих параграфах, плоская волна и соответствующие ей коэффициенты отражения и преломления характеризовались парой чисел 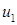 и и  , а не с помощью угла падения или скольжения, поскольку для удобства последующих расчетов, с применением быстрого алгоритма преобразования Фурье, удобно поступить именно так. Найдем соответствующие коэффициенты отражения и преломления как функции , а не с помощью угла падения или скольжения, поскольку для удобства последующих расчетов, с применением быстрого алгоритма преобразования Фурье, удобно поступить именно так. Найдем соответствующие коэффициенты отражения и преломления как функции 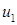 и и  , т.е. именно в таком виде, в котором они фигурируют в формулах из предыдущих параграфов. , т.е. именно в таком виде, в котором они фигурируют в формулах из предыдущих параграфов.
Рис. 2. К выводу френелевских коэффициентов отражения и прохождения для однородных и неоднородных плоских волн.
Пусть на поверхность раздела падает плоская волна, задаваемая уравнением (23) (рис. 2). Решение задачи будем искать в виде трех волн: падающей и отраженной в верхнем полупространстве и преломленной в нижнем полупространстве, причем отраженную и преломленную плоские волны запишем в виде
 , (26) , (26)
 . (27) . (27)
В формулах (26) и (27) векторы  , ,  в общем случае являются комплексными. в общем случае являются комплексными.
На границе раздела двух сред должны удовлетворяться граничные условия [10]
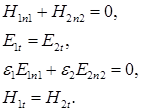 (28) (28)
В выражении для граничных условий (28) первый встречающийся индекс обозначает среду: 1 – верхнее полупространство, 2 – нижнее; индекс  , ,  – обозначают проекцию на нормаль, проведенную в верхнюю и нижнюю среду соответственно; индекс – обозначают проекцию на нормаль, проведенную в верхнюю и нижнюю среду соответственно; индекс 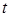 – обозначает проекцию на касательный к границе раздела вектор. – обозначает проекцию на касательный к границе раздела вектор.
Для комплексных амплитуд горизонтальной поляризации отраженной и прошедшей волн получаются следующие выражения
 , (29) , (29)
 , (30) , (30)
в которых 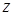 – компоненты комплексного волнового вектора в каждой среде связаны с – компоненты комплексного волнового вектора в каждой среде связаны с  и и  соотношениями аналогичными (25). Индекс соотношениями аналогичными (25). Индекс 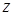 при этом обозначает третью компоненту при этом обозначает третью компоненту  в соответствующей среде. Таким образом, могут быть получены следующие формулы для коэффициентов прохождения и отражения для любого типа плоских волн в соответствующей среде. Таким образом, могут быть получены следующие формулы для коэффициентов прохождения и отражения для любого типа плоских волн
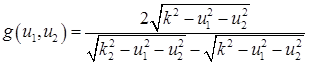 ,(31) ,(31)
 ,(32) ,(32)
в которых знаки перед корнями должны выбираться с учетом требуемых проекций  – компонент волновых векторов на оси координат. – компонент волновых векторов на оси координат.
Радиоголограмма точечного источника
В качестве примера рассчитаем с использованием приведенных выше формул голограмму точечного рассеивателя, находящегося в нижнем полупространстве. Предположим, что в качестве сигнала, регистрируемого радиолокатором, будет являться модуль суммы отраженных сигналов от точечного рассеивателя, находящегося под поверхностью, поверхности и некоторого постоянного опорного сигнала, подаваемого непосредственно из передатчика в приемник. Таким образом, голограммой будем называть модуль суммы
 ,(33) ,(33)
где введены обозначения 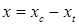 , , 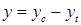 . В выражении (33) . В выражении (33)  задается (17), а задается (17), а 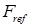 – комплексная величина опорного сигнала. – комплексная величина опорного сигнала.
Так как выбор опорного сигнала допускает некоторый произвол, то сумма сигнала отраженного от поверхности и опорного может принимать любое значение. Для следующего примера в качестве опорного сигнала выбиралось действительное число, равное максимуму модуля сигнала, отраженного от точечного источника. Получившаяся в результате моделирования голограмма изображена на рис. 3.
На осях координат отложено смещение центра апертуры радиолокатора от проекции точечного рассеивателя на поверхность  . Величины используемых при расчете голограммы параметров приводятся в таблице 1. . Величины используемых при расчете голограммы параметров приводятся в таблице 1.
Таблица 1. Величины параметров модели, используемых при моделировании голограммы
| Параметр
|
Значение
|
| Размер сетки дискретизации
|
256х256
|
| Излучаемая длина волны в воздухе, см
|
7
|
| Глубина, на которой находился точечный рассеиватель, см
|
4
|
| Комплексная диэлектрическая проницаемость нижнего полупространства
|
4 + 2i
|
| Комплексный коэффициент отражения, приведенный в (17)
|
1
|
| Распределение комплексной амплитуды по апертуре
|
постоянное синфазное
|
| Моделируемая апертура
|
круговая
|
| Размеры апертуры, радиус, см
|
5.25
|
Как видно на рис. 3, голограмма, полученная с помощью радиолокатора, имеет небольшое количество осцилляций из-за того, что апертурная антенна радиолокатора является направленной. Отметив, что эффективный размер области, в которой сосредоточено отраженное от точечного источника поля имеет размер, сопоставимый с размером самой антенны, диаметр которой равен примерно 10 см, можно сделать вывод о том, что для восстановления изображения источника такая антенна не даст хорошей фокусировки изображения. Данное обстоятельство объясняется тем, что размер получаемой голограммы ограничивает дифракционный предел синтезированной апертуры. Таким образом, для такого типа радиолокаторов необходимо использовать ненаправленные антенны при зондировании малозаглубленных предметов, что привело бы к тому, что полученная голограмма имела бы значительно больший размер.
В следующем параграфе рассмотрена возможность восстановления распределения источников по регистрируемой голограмме методом восстановления волнового фронта.
Восстановление голограммы
Пусть  распределение комплексной амплитуды поля в плоскости распределение комплексной амплитуды поля в плоскости 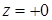 (рис. 1), тогда комплексную амплитуду выходного сигнала антенны можно выразить по формуле (рис. 1), тогда комплексную амплитуду выходного сигнала антенны можно выразить по формуле
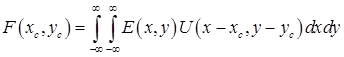 , (34) , (34)
где весовая функция 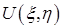 является характеристикой антенны радиолокатора. Выражение (34) является интегральным уравнением свертки относительно неизвестного распределения комплексной амплитуды поля является характеристикой антенны радиолокатора. Выражение (34) является интегральным уравнением свертки относительно неизвестного распределения комплексной амплитуды поля  . Применяя интегральное преобразование Фурье к обеим частям уравнения (34), можно выписать формальное решение в следующем виде . Применяя интегральное преобразование Фурье к обеим частям уравнения (34), можно выписать формальное решение в следующем виде
 , (35) , (35)
где 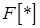 , ,  – прямое и обратное преобразование Фурье соответственно. – прямое и обратное преобразование Фурье соответственно.
В выражении (35) обратное преобразование Фурье отношения может и не существовать в силу того, что  может иметь нули, а может иметь нули, а 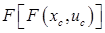 может иметь высокочастотные гармоники, обусловленные, например, шумом. может иметь высокочастотные гармоники, обусловленные, например, шумом.
Уравнение (34) должно быть регуляризовано введением в оператор обращения дополнительного множителя, позволяющего построить приближенное решение.
Методика решения уравнения свертки (34) введением регуляризирующего множителя, согласованного с погрешностями задания левой части хорошо известна [11]. Поэтому далее с целью упрощения задачи будем считать, что распределение комплексной амплитуды поля, создаваемое источниками, находящимися в нижнем полупространстве, известно. Последнее утверждение эквивалентно использованию точечной антенны вместо апертурной (рис. 1).
Рассмотрим алгоритм получения изображения точечного источника, находящегося на некоторой глубине в однородной среде, характеризуемой комплексным волновым вектором k
, как изображено на рис. 4. Положение точечного рассеивателя в нижнем пространстве задается вектором  , текущее положение точечного приемопередатчика задается вектором , текущее положение точечного приемопередатчика задается вектором  . Комплексная амплитуда поля, регистрируемая приемной антенной на поверхности раздела, задаваемой . Комплексная амплитуда поля, регистрируемая приемной антенной на поверхности раздела, задаваемой  , представим в виде , представим в виде
 , (36) , (36)
где комплексный коэффициент  характеризует отражательные свойства точечного источника, характеризует отражательные свойства точечного источника, 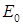 – комплексная амплитуда возбуждения передатчика. Дополнительный множитель 2 в показателе экспоненте и квадрат разности векторов в знаменателе возникают в предположении того, что точечный источник отражает волну, приходящую от точечного облучателя. – комплексная амплитуда возбуждения передатчика. Дополнительный множитель 2 в показателе экспоненте и квадрат разности векторов в знаменателе возникают в предположении того, что точечный источник отражает волну, приходящую от точечного облучателя.
Рис. 4. Расположение точечных приемопередатчика и отражателя.
В результате перемещения антенны по плоскости раздела может быть получено двумерное распределение комплексной амплитуды  . .
Приведенный пример записи распределения комплексной амплитуды допускает аналогию с записью оптической голограммы с тем лишь отличием, что при записи голограммы в оптике источник, освещающий предмет, как правило, является неподвижным. В данном случае, при записи распределения комплексной амплитуды передатчик перемещается вместе с антенной, что приводит к появлению коэффициента 2 в выражении (36).
Если бы мы имели дело со случаем, когда точечный источник, находящийся в нижнем полупространстве, излучал бы самостоятельно, то двумерное распределение комплексной амплитуды задавалось бы соотношением
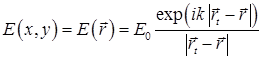 , (37) , (37)
в котором комплексный коэффициент  задает фазу и амплитуду возбуждения. В таком случае восстановление изображения заключалось бы в том, что нужно было бы взять распределение задает фазу и амплитуду возбуждения. В таком случае восстановление изображения заключалось бы в том, что нужно было бы взять распределение  , комплексно сопряженное (37), и рассчитать комплексную амплитуду поля, которая создается распределением , комплексно сопряженное (37), и рассчитать комплексную амплитуду поля, которая создается распределением 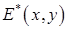 в нижнем полупространстве. Очевидно, что это распределение фокусируется как раз в месте расположения точечного источника. в нижнем полупространстве. Очевидно, что это распределение фокусируется как раз в месте расположения точечного источника.
Распределение, задаваемое (36), тоже может быть «сфокусировано» в действительном месте расположения точечного источника. Для этого заметим, что распределение, задаваемое (36) будет иметь фокус в месте расположения источника, если данное распределение создается волной, характеризуемой волновым вектором  . В оптике это соответствовало бы восстановлению голограммы опорной волной с вдвое меньшей длиной волны. . В оптике это соответствовало бы восстановлению голограммы опорной волной с вдвое меньшей длиной волны.
Для того чтобы найти распределение комплексной амплитуды в нижнем полупространстве на глубине 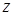 , воспользуемся спектральным методом. Спектр плоских волн распределения комплексной амплитуды , воспользуемся спектральным методом. Спектр плоских волн распределения комплексной амплитуды  представляется в виде представляется в виде
 .(38) .(38)
Спектр плоских волн (38), пройдя слой пространства толщиной  в противоположном направлении оси в противоположном направлении оси  преобразуется по известному соотношению преобразуется по известному соотношению
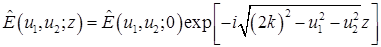 ,(39) ,(39)
где использование вдвое большего волнового числа объяснялось выше.
Распределение комплексной амплитуды, соответствующее спектру, получается с помощью обратного преобразования Фурье
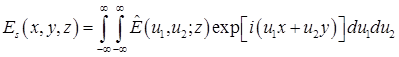 .(40) .(40)
Рассмотрим пример построения распределений модуля комплексной амплитуды  для точечного приемопередатчика и точечного источника, расположенного на некоторой глубине. Будем использовать соотношения (36), (38) – (40), а также быстрый алгоритм преобразования Фурье для вычисления интегралов (38) и (40). для точечного приемопередатчика и точечного источника, расположенного на некоторой глубине. Будем использовать соотношения (36), (38) – (40), а также быстрый алгоритм преобразования Фурье для вычисления интегралов (38) и (40).
На рис. 5 изображен пример восстановления изображения заглубленного объекта в виде прямоугольной рамки со стороной размером 3 см с использованием приведенных выше соотношений. Рамка располагалась на глубине 6 см от поверхности раздела. Комплексная диэлектрическая проницаемость полупространства, в котором находится объект, задавалась равной 12 + i
. Длина волны в свободном пространстве принималась равной 5 см. Видно, что в действительном месте расположения объекта (рисунок с заглавием focusing
at
– 6 cm
) имеет место фокусировка изображения, что приводит к возможности определить форму и размеры заглубленного предмета.
При получении изображений на рис. 5 использовалась фильтрация в спектральной области, суть которой заключается в подавлении интенсивной прошедшей волны при восстановлении голограммы. Фильтрация не приводит к дополнительным вычислениям и заключается в обнулении соответствующего коэффициента при вычислении спектра в выражении (39) с помощью БПФ.
Следует отметить, что на результат восстановления изображения не влияет неизвестное изменение фазы при отражении волны от заглубленного предмета, что является преимуществом данного метода по сравнению с восстановлением изображения корреляционными методами, о которых говорилось во введении.
Изображения, приведенные на рис. 5, были получены по известному распределению комплексной амплитуды отраженного поля на поверхности раздела, что соответствует использованию обоих квадратурных компонент принятого сигнала. В случае амплитудного детектора, на восстанавливаемое действительное изображение заглубленного объекта накладывается расфокусированное мнимое изображение.
Рис. 5. Пример восстановления изображения заглубленного предмета методом восстановления волнового фронта.
Для неплоских заглубленных предметов, применение данного алгоритма позволит получать картину о распределении комплексной амплитуды поля в непосредственной близости от заглубленного предмета, что будет давать более близкое представление о нем, чем необработанные данные, регистрируемые у поверхности раздела.
В статье предложена модель сигнала, принимаемого подповерхностным радиолокатором с апертурной антенной при отражении от точечного рассеивателя, укрытого в однородной поглощающей среде. Построена модель опорного сигнала, возникающего при отражении от поверхности раздела. Предложена алгоритм обработки сигнала, позволяющий восстанавливать изображение заглубленных предметов по регистрируемым на поверхности раздела голограммам. Использование квадратурного детектора позволило бы при восстановлении получать только действительное изображение без влияния мнимого, либо наоборот. При этом возможно определение глубины залегания предмета с использованием немодулированного зондирующего сигнала.
|