| Московский Государственный институт путей сообщения
(МИИТ)
Воронежский филиал
Контрольная работа
по дисциплине: «Динамика вагонов»
Воронеж 2010
СОДЕРЖАНИЕ
Часть 1
1. Определение собственных частот колебаний вагона
2. Расчет параметров гасителей колебаний
3. Проверка рессорного подвешивания на отсутствие «валкости»
4. Составление дифференциального уравнения вынужденных колебаний подпрыгивания вагона и нахождение аналитического выражения описывающего процесс вынужденных колебаний подпрыгивания вагона
Часть 2
1. Расчет динамических боковых и рамных сил при вписывании вагона в кривых участках пути
2. Расчет наибольших боковых и рамных сил возникающих при извилистом движении вагона в прямых участках пути и при выходе его в кривую
3. Расчет наибольших сил инерции необрессоренных масс вагона при проходе колесом стыка и движении колеса с ползунами на поверхности катания
Часть 3
1. Расчет запасов устойчивости вагона и устойчивости сдвигу рельсошпальной решетки и от схода колес вагона с рельса при действии продольных сил в поезде
Исходные данные
| Тип вагона
|
Хоппер грузоподъемностью 50 т
|
| Тара вагона Gтар
, т
|
21
|
| Грузоподъемность Gгр
, т
|
50
|
| База вагона L, м
|
5,081
|
| Длинна вагона Lв
, м
|
10,03
|
| Боковая поверхность кузова вагона (площадь ветрового «паруса») F, м
|
25
|
| Высота центра ветровой поверхности кузова относительно центра колеса hв
, м
|
1,87
|
| Условное обозначение и тип тележки
|
1
|
| База тележки lт
,
|
1,8
|
| Вес тележки Gтел
, Н
|
45,70
|
| Вес необрессоренных частей, приходящихся на колесо q, Н
|
9,75
|
| Наибольший прогиб рессорного комплекта с1
, кН/м
|
10000
|
| Полярный момент инерции тележки, относительно вертикальной оси, проходящей через центр I0
, Н*м*с2
|
0,595*105
|
| Тип гасителя колебаний
|
Fгас
=-Fтр
signZ
|
| Использование грузоподъемности вагона a, %
|
0
|
| Высота центра тяжести кузова с грузом над уровнем рессорного подвешивания hц
, м
|
1.1
|
| Момент инерции вагона с грузом относительно оси, проходящей в плоскости верха рессор и направленной:
а) параллельно оси пути Ix
, Н*м*с2
* 104
б) перпендикулярно оси пути Iy
, Н*м*с2
*104
|
5.9
14.9
|
| Скорость движения вагона v, км/ч
|
50
|
| Длина периода неровности пути lн
, см
|
1250
|
| Радиус круговой кривой R, м
|
800
|
| Длина переходной кривой lн
, м
|
75
|
| Амплитуда неровностей пути h, см
|
0.95
|
| Угол, образуемый концами рельсов в стыке при перекатывании колеса через стык g, рад
|
0,021
|
| Длина ползуна на колесе а, мм
|
22
|
| Масса пути, взаимодействующая с колесом при ударе ползуна m, Н*с/м*103
|
0,09
|
| Боковая жесткость пути сп
, 106
H/м
|
28,9
|
| Величина сжимающего продольного усилия в поезде S, кН
|
200
|
| Разность высот автосцепок у соседних вагонов в hа
, мм
|
100
|
ЧАСТЬ 1
1.
Определение собственных частот колебаний вагона
Круговая частота собственных колебаний вагона определяем по формуле:
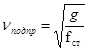 (1) (1)
где g = 9, 81 м/с2
– ускорение свободного падения;
fст
– статический прогиб рессор.
Статический прогиб рессор определяем по формуле:
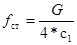 (2) (2)
где G – вес кузова вагона;
с1
– жесткость одного рессорного комплекта.
Вес кузова вагона определяем по формуле:
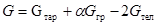
где Gтар
– тара вагона;
Gгр
– грузоподъемность вагона;
a - доля использования грузоподъемности вагона;
Gтел
– вес тележки.
G = 210000+0*50-2*45,70 = 209908,6 Н
fст
= 209908,6/4*1000000 = 0,052 м
 (3) (3)
Тогда период колебаний подпрыгивания будет равен:
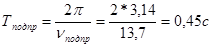 (4) (4)
Угловую частоту собственных колебаний галопирования кузова вагона находим по формуле:
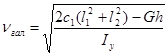 (5) (5)
где l1
+l2
= L – база вагона;
h – высота центра тяжести вагона с грузом над уровнем рессорного подвешивания
Iy
– момент инерции вагона с грузом относительно оси, проходящей в плоскости верха рессор и направленной перпендикулярно оси пути.
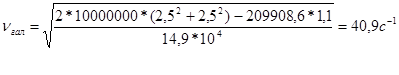
Тогда
 (6) (6)
Из формулы 7 следует, что чем меньше жесткость рессорного подвешивания с1
, чем больше момент инерции кузова Iy
и выше центр тяжести h, тем меньше частота собственных колебаний галопирования nгал
и тем больше период галопирования Tгал
.
Колебания боковой качки могут быть рассмотрены с помощью той же схемы, приняв в ней вместо l1
и l2
величины b1
и b2
и вместо момента инерции кузова вагона Iy
(относительно оси y) – момент инерции кузова вагона относительно оси x – Ix
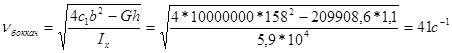
Тогда период колебаний будет равен
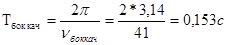
Линейные частоты колебаний кузова определяются по формуле:

Тогда

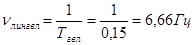

Следовательно, чем больше величина частоты, тем больше плавность хода вагона.
2.
Расчет параметров гасителей колебаний
Задан гаситель с постоянной силой трения

где Nтр
– нормальная сила (нажатие) в трущейся паре гасителя;
j - коэффициент трения частей пары.
3.
Проверка рессорного подвешивания на отсутствие «валкости»
Для определения высоты метоцентра рассмотрим вагон, вес кузова которого G и жесткость рессоры с. Тогда, реакции рессорных комплектов при наклоне кузова на угол q составят:

Момент реакции рессор относительно точки О1

Заменим действие силы R1
и R2
их равнодействующей R, а точку пересечения равнодействующей в наклонной осью вагона назовем метацентром вагона. Момент равнодействующей R относительно точки O1

где hМ
– высота метацентра от пола вагона.
Поскольку угол q мал, то tgq»0, т.е. M0
=RhM
q, где R = R1
+ R2
= Q, то приравнивая момент силы R1
и R2
моменту от их равнодействующей R, получим qhM
G = 2b2ec
q, отсюда
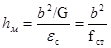
где fст
– статический прогиб рессорного подвешивания вагона;
b – половина базы тележки.

Высота метацентра выше центра тяжести вагона более чем на 2 м, следовательно вагон устойчив.
4. Составление дифференциального уравнения вынужденных колебаний подпрыгивания вагона и нахождение аналитического выражения описывающего процесс вынужденных колебаний подпрыгивания вагона
Решение дифференциального уравнения n = 2p/Т является аналитическим выражением процесса вынужденных колебаний подпрыгивания вагона при движении его по регулярным неровностям вида z = hcoswt.
Это решение имеет вид:

где n - скорость движения вагона;
lн
– длинна периода неровностей;
2h – высота неровностей;
n - круговая частота собственных колебаний
Для колеса вагона номер i возмущение функции имеет вид:

где li
– расстояние от первого до i-го колеса.
Амплитуда вынужденных колебаний подпрыгивания кузова вагона будет иметь вид:

Для заданного вагона
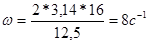
Аналитическое выражение описывающее процесс вынужденных колебаний будет иметь вид:

Для построения графика определяем зависимость z от t

При t=1 сек
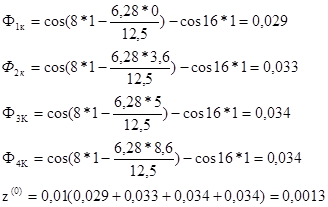
Для других значений t

ЧАСТЬ II
1. Расчет динамических боковых и рамных сил при вписывании вагона в кривых участках пути
Наибольшие боковые силы возникают тогда, когда при движении вагона наибольшее допустимое непогашенное ускорение на вагон достигает 0,7 м/с2
. Это возможно при минимально допустимом для этой кривой возвышении наружного рельса. Его можно определить используя формулу:
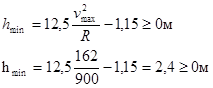
Величина действующей на одну тележку поперечной горизонтальной силы:
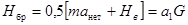
где m – масса вагона;
анет
– непогашенное поперечное ускорение;
Hв
– сила ветра, действующая на вагон и направленная поперек пути
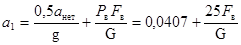
Принимая aнет
= 0,8 м/с2
, получим
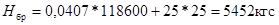
При действии на вагон продольных сил S, которые могут возникнуть, например при рекуперативном напряжении на шкворень тележки действуют дополнительная сила Hторм
которая приближенно равна:
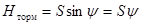
Наибольший угол y можно определить по формуле:

Общее усилие на шкворень в этом случае
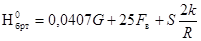
где S – продольное усилие в поезде;
2k – расстояние между клиновыми отверстиями автосцепок.

Поскольку, в своем движении по кривой тележка непрерывно вращается вокруг полюса поворота, то образующийся от силы H0
брт
момент относительно точки О уравновешивается направляющим усилием Y (давление гребня набегающего колеса первой оси тележки на боковую поверхность) поперечными силами трения колес по рельсам.

где P – вертикальная нагрузка, передаваемая колесом рельсу;
m - коэффициент трения колесом по рельсу (принимаем m = 0,25).
Уравнение проекций этих сил имеет вид:
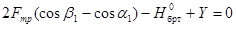
Положение центра поворота в общем случае находим методом попыток. Для двухосной тележки по графику [2] определяем расстояние от шкворня до точки О в зависимости от отношения  . Из рисунка 4 видно, что . Из рисунка 4 видно, что

где s1
= 1,6 м – расстояние между осями рельсов;
lТ
– база тележки (180 см).
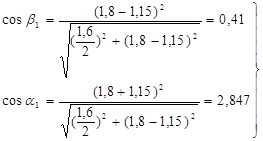
Определим направляющее усилие Y
Боковая сила определяется из уравнения
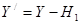
а рамная сила

где

2. Расчет наибольших боковых и рамных сил возникающих при извилистом движении вагона в прямых участках пути и при выходе его в кривую
Наибольшую величину боковой силы Y при извилистом движении в прямом участке определяют по формуле:
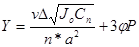
где nD=40 мм – зазор между рабочими гребнями колес и рельсами;
J0
= 0,595*104
– полярный момент инерции тележки относительно вертикальной оси проходящей через центр;
n = 1/20 – наклон образующей конуса и оси;
Сn
= 19,1*106
кгс/м – боковая жесткость пути;
j = 0,25 – коэффициент трения поверхности обода по рельсу.

Рамная сила:
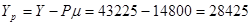
Определим боковую силу при входе вагона в кривые участки пути

где 
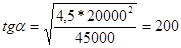
Параметр переходной кривой Cпер
следует рассчитывать по заданному радиусу R круговой кривой и l0
– длине переходной кривой и до ближайшего числа кратного 5000 м2
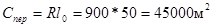

Рамная сила

3. Расчет наибольших сил инерции необрессореных масс вагона при проходе колесом стыка и движении колеса с ползунами на поверхности катания
Наибольшая величина силы инерции необрессореных масс вагона рассчитывается по формуле:

где vk
– cкорость удара колеса о рельс;
Cк
= 5*105
кгс/см – контактная жесткость;
mn
= 100 кгс/g – масса пути.
Необходимо предварительно определить скорость удара колес по рельсу. Она равна при движении колес с ползуном

При прохождении стыка, в котором рельсы при прогибе образуют угол g

Часть III
Расчеты запасов устойчивости вагона и устойчивости сдвигу рельсошпальной решетки и от схода колес вагона с рельса при действии продольных сил в поезде
Для расчета устойчивости движения колес по рельсу следует определить величины нагрузок, передаваемых на шейки колесной пары P1
и Р2
.
Кроме статической нагрузки на шейке колесной пары передаются усилия вызванные колебаниями надрессорного строения. Наиболее выгодным положением с точки зрения устойчивости колеса на рельс будет случай, когда в целом колесная пара разгружается колебаниями галопирования и подпрыгивания, а в колебаниях боковой качки обезгружено колесо, набегающее на наружный рельс кривой.
Если общий динамический коэффициент колебаний надрессорного строения равен KДО
= 0,277, в боковой качки Кбк
= 0,09
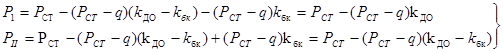
где q = 975 кгс – необрессоренный вес, приходящийся на одно колесо;
PСТ
– нагрузка от колеса на рельс.
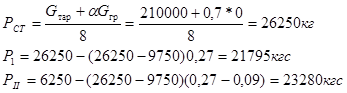
Кроме того, за счет действия непогашенного ускорения и ветровой нагрузки произойдет перегрузка шейки колеса идущего по наружной грани нити и разгрузка шейки колеса, идущего по внутренней нитке. Если центр тяжести кузова находится на hц от головки рельса, а центр ветровой поверхности на высоте hв от головки рельса, то момент опрокидывающих сил будет равен:

Момент удерживающих сил

где b – расстояние между серединами шеек колесной пары (203,6 см)
DP1
– величина нагрузки колеса, идущего по наружному рельсу, или величина разгрузки колеса, идущего по внутреннему рельсу

При разности высот автосцепок у соседних вагонов Dha
=75 мм и при действии на вагон продольных сил S происходит разгрузка тележки, которая равна 
Если разница в высоте автосцепок соседних вагонов равна Dhа
, то

где Lв
– длинна вагона
k – 6,365 м – половина расстояния между клиновыми отверстиями автосцепок

Так как разгрузки DР1
и DР2
распределяются на четыре колеса тележки, то
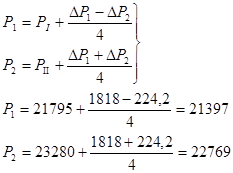
Зная Р1
, Р2
и Yр
можно определить коэффициент запаса устойчивости колесной пары по вползанию гребня колеса на рельс
С учетом размеров колесной пары b1
= 0,228 м; b2
= 1,808 м; R = 0,475 м; r = 0,075 м
Определение устойчивости пути поперечному сдвигу.
Для определения устойчивости рельсовой решетки поперечному сдвигу при заданных расчетных данных следует применять условие  , где , где

Условие 52279 т £ 210000т соблюдается. Рельсовая решетка устойчива поперечному сдвигу.
|