Контрольная работа: Расчет параметров электрических схем

1. Расчет линейной цепи постоянного тока

Задание :

1. Рассчитать схему по законам Кирхгофа.

2. Определить токи в ветвях методом контурных токов.

3. Определить ток в ветви с сопротивлением R₁ методом эквивалентного генератора.

4. Составить уравнение баланса мощностей и проверить его подстановкой числовых значений.

5. Определить показание вольтметра.

Расчет линейной цепи постоянного тока

E2= -53B R1= 92Ом R4= 96Ом

E5= 51B R2= 71Ом R5= 46Ом

E6= -29B R3= 27Ом R6= 53Ом

Расчёт схемы по законам Кирхгофа

I_1-6 – ?

Количество уравнений составляется по первому закону Кирхгофа (сумма входящих в узел токов равен сумме исходящих токов из узла)

n₁ =у-1=4–1=3; n₁ – количество уравнений по 1-му закону Кирхгофа

у – число узлов

1. I₆ +I₅ = I₂

2. I₅ +I₄ =I₁ ,

3. I₃ +I₆ = I₄ ;

Составим уравнения по второму закону Кирхгофа (алгебраическая сумма падений напряжения в контуре равен алгебраической сумме ЭДС в этом же контуре.)

n₂ =B-у+1-B_I =6–4+1=3; n₂ – количество уравнений по 2-му закону Кирхгофа

В-число ветвей; В₁ – число ветвей содержащих источник тока

I. – R₅ I₅ +R₆ I₆ +R₄ I₄ = E₆ +E₅ ,

II. R₂ I₂ +R₁ I₁ +R₅ I₅ = E₂ -E₅ ,

III. R₄ I₄ +R₁ I₁ +R₃ I₃ =0;

96I₄ -46I₅ +53I₆ = -29+51,

92I₁ +71I₂ +46I₅ = -53–51,

92I₁ +27I₃ +96I₄ =0;

I₂ -I₅ -I₆ =0,

I₄ +I₅ -I₁ =0,

I₃ -I₄ +I₆ =0.

Решим систему уравнений с помощью Гаусса.

I₁ = -0,30609 А

I₂ = -0,76306 А

I₃ = 0,45697 А

I₄ = 0,16482 А

I₅ = -0,47091 А

I₆ = -0,29215 А

Метод контурных токов

Контурный ток – это некоторая величина, которая одинакова для всех ветвей контура.

I₁₁ , I_22, I₃₃ – ?

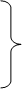I₁₁ R₁₁ +I₂₂ R₁₂ …+…I_mm R_1m =E₁₁

I₁₁ R₂₁ +I₂₂ R₂₂ …+…I_mm R_2m =E₂₂

………………………………. – общий вид

I₁₁ R_{m 1} +I₂₂ R_{m 2} …+…I_mm R_mm = E_mm

Для моего случая:

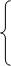I₁₁ R₁₁ + I₂₂ R₁₂ +I₃₃ R₁₃ =E₁₁

I₁₁ R₂₁ + I₂₂ R₂₂ +I₃₃ R₂₃ = E₂₂

I₁₁ R₃₁ + I₂₂ R₃₂ + I₃₃ R₃₃ = E₃₃

R_11, R₂₂ , R_33, – собственное сопротивление контуров, вычисляется как сумма сопротивления ветвей входящих в данный контур.

R₁₁ =R₆ +R₅ +R₄

R₂₂ =R₁ +R₅ +R₂

R₃₃ =R₄ +R₃ +R₁

R₁₂ =R_21, R₁₃ =R_31, R₂₃ =R₃₂ - общее сопротивление для 2-х контуров, вычисляется как сумма сопротивлений входящих в 2 смежных контура.

R₁₂ =R₂₁ =R₅

R₁₃ =R₃₁ =R₄

R₂₃ =R₃₂ =R₁

E₁₁ , E₂₂ , E₃₃ – собственная ЭДС контура, вычисляется как алгебраическая сумма всех входящих в контур ЭДС, причём ЭДС берется со знаком «+», если направление контура тока и ЭДС источника со направлены и «–» если противоположно направлены.

E₁₁ = E₆ +E₅

E₂₂ =E₂ – E₅

E₃₃ =0

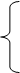I₁₁ (R₆ +R₅ +R₄ ) – I₂₂ R₅ +I₃₃ R₄ = E₆ +E₅ ,

– I₁₁ R₅ +I₂₂ (R₁ +R₅ +R₂ )+I₃₃ R₁ =E₂ –E₅ ,

I₁₁ R₄ +I₂₂ R₁ +I₃₃ (R₄ +R₃ +R₁ )=0;

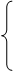I₁₁ (53+46+96) – I₂₂ 46+I₃₃ 96= -29+51, 195 I₁₁ -46 I₂₂ + 96 I₃₃ = 22,

– I₁₁ 46+I₂₂ (92+46+71)+I₃₃ 92=-53–51, -46 I₁₁ +209 I₂₂ +92 I₃₃ = -104,

I₁₁ 96+I₂₂ 92+I₃₃ (96+27+92)=0; 96 I₁₁ + 92 I₂₂ +215 I₃₃ = 0;

Решим систему уравнений с помощью Гаусса и найдем I_1-6

I₁₁ = – 0,29215 A

I₂₂ = -0,76306 A

I₃₃ = 0,45697A

I₆ =I₁₁ = – 0,29215 А

I₂ =I₂₂ = -0,76306 A

I₃ = I₃₃ = 0,45697 A

I₄ =I₁₁ + I₃₃ = 0,16482 A

I₅ = – I₁₁ + I₂₂ = -0,47091 A

I₁ =I₂₂ +I₃₃ = -0,30609

Метод эквивалентного генератора

Разомкнем ветвь, в которой необходимо найти ток и представим эту разомкнутую цепь в виде эквивалентного генератора.

I₁ =E_ЭКВ /(R₁ +R_ВН ); R_эк = R_ВН

Для определения напряжения холостого хода воспользуемся первым и вторым законами Кирхгофа.

R ₁₁ I^’ ₁₁ +R₁₂ I^’ ₂₂ = E₅ +E₆ ,

R₂₁ I^’ ₁₁ +R^’ ₂₂ I^’ ₂₂ = E₂ +E₆ ,

(R₄ +R₅ +R₆ ) I^’ ₁₁ +R₆ I^’ ₂₂ = E₅ +E₆ ,

R₆ I^’ ₂₂ +(R₂ +R₃ +R₆ )*I^’ ₂₂ = E₂ +E₆ ,

R₄ I^’ _4xx + R₃ I^’ _3xx + U_xx = 0

U_XX =(R₁ +R_ВН ) I₁

Определим внутреннее сопротивление эквивалентного генератора.

Воспользуемся методом входных сопротивлений, при этом сопротивление определяется относительно разомкнутой электрической цепи.

Для расчета из цепи устраняем все источники.

R₇ = R₄ *R₅ /(R₄ +R₅ +R₆ )=96*46/(96+46+53)=23 Ом

R₈ = R_5* R₆ /(R₄ +R₅ +R₆ )=53*46/(96+46+53)=12,5 Ом

R₉ = R₄ *R₆ /(R₄ +R₅ +R₆ )=96*53/(96+46+53)=26 Ом

R₈ и R₂ соединены последовательно. R₁₀ =R₇ +R₂ = 83,5 Ом

R₉ и R₃ соединены последовательно. R₁₁ =R₉ +R₃ = 53 Ом

R₁₀ и R₁₁ соединены параллельно

R₁₂ =R₁₁ *R₁₀ /(R₁₁ +R₁₀ )=83,5*53/(83,5+53)=33,6 Ом

R₇ и R₁₂ соединены последовательно.

R_эк = R_ВН = R₁₂ +R₇ =33,6 + 23=56,6 Ом

195 I^’ ₁₁ +53 I^’ ₂₂ = 51–29

53 I^’ ₁₁ +151 I^’ ₂₂ =-53–29

I^’ ₁₁ = I_4xx

I^’ ₂₂ =-I_3xx

I^’ ₁₁ =I_4xx = 0,28788 А

I^’ ₂₂ =-I_3xx = 0,64409 А

U_xx = – (R₄ I^’ _4xx + R₃ I^’ _3xx )= – (96*0,28788 +27*0,6449)=-45,027 В

I^' ₁ =U_xx /(R_эк +R₁ )=(-45,027)/(56,6+92)= -0,30301 А

Баланс мощностей

∑ P_ист = ∑ P_потр

P_ист =E₂ I₂ -E₅ I₅ +E₆ I₆ =(-52)*(-0,76306)+51*(-0,47091)+ (-29)*(-0,29215)= 72,9309 Вт

P_потр =I₁ ² R₁ +I₂ ² R₂ +I₃ ² R₃ +I² ₄ R₄ +I₅ ² R₅ +I₆ ² R₆ =(-0,30609)² *92+(-0,76306)² *71+(0,45697)² *27+ (0,16482)² *96+(-0,47091)² *46+(-0,29215)² *53=72,9309Вт

72,9309=72,9309 баланс соблюдается

Определим показание вольтметра по закону Кирхгофа:

U_v +I₅ R₅ =E₂ – E₅

U_v =E₂ – I₅ R₅ – E₅ = – 53 – 51 – (-0,76306)*46= -69 В

pV= -69 В

2. Расчет электрической цепи однофазного переменного тока

Задание:

1. Определить комплексные действующие значения токов в ветвях схемы.

2. Определить показание приборов.

3. Составить баланс активных, реактивных и полных мощностей.

4. Повысить коэффициент мощности до 0,98 включением необходимого реактивного элемента Х .

5. Построить векторные диаграммы токов и напряжений в одной системе координат.

Расчет электрической цепи однофазного переменного тока

Исходные данные :

U=100В R1=24Ом L1=83мГн C1=230мкФ

F=200Гц R2=15Ом L2=0 C2=73мкФ

Определим комплексные действующие значения токов в ветвях схемы.

X_{L 1} =2π*FL₁ =2*3,14*200*83*10^-3 =104,25 Ом

X_{C 1} =1/(2π*FC₁ )= 1/(2*3.14*200*230*10^-6 )=3,46 Ом

X_{C 2} =1/(2π*FC₂ )= 1/(2*3.14*200*73*10^-6 )=10,91 Ом

Z ₁ =R₁ +j(X_{L 1} -X_{C 1} )=24+j (104,25–3,46)=24+j100,79=103,6*e^{j 76,6} Ом

Z ₂ =R₂ -jX_{С 2} =15-j10,91_{_} =18,55*e^-j36° Ом

I ₁ =U / Z ₁ ; I ₂ =U / Z ₂

I ₁ =100e^j0 /103,6*e^j76,6 =0,96e^-j76,6 =0,96 (cos(-76,6)+j sin (-76,6))=(0,22 – j0,93) А

I ₂ =100e^j0 /18,55*e^-j36° =5,39e^j36 =5,39 (cos36+j sin36)=(4,36+j3,17) А

I ₃ =I ₁ +I ₂ =0,22 – j0,93+4,36+j3,17=4,58+j2,24=5,1e^{j 26,1º} А

2. Определим показание приборов

Показания амперметров:

pA₁ =I₁ =0,96A

pA₂ =I₂ =5,39A

pA₃ = I₃ =5,1A

Показание фазометра:

pφ= φ_u – φ_{i 3} =0–26,1=-26,1^°

Показание ваттметра

pW=Re [U *I ₃ ^* ]=100*5,1*cos (-26,1)=458 Вт

Показание вольтметра

Напряжение на вольтметре найдем по закону Кирхгофа:

I ₂ R₂ +U _V – I ₁ j(X_L1 -X_C1 )=0

U _V =I ₁ j(X_L1 -X_C1 ) – I ₂ R₂

U _V = j100,79 (0,22 – j0,93) – 15 (4,36+j3,17)=22,2j+93,73–65,4–47,55j=

=28,33–25,35j=38e^-j41,8 B

pV=38 B

3. Составим баланс активных, реактивных и полных мощностей

S _ист . =S _пр.

S _ист. =U _. *I ₃ ^* =100e^{j 0} *5,1e^{- j 26,1º} =510 e ^{– j 26,1°} = (458 – j224,37) BA

P_ист = 458Вт; Q_ист = -224,37 ВАр

S _пр = P_пр. +j Q _{пр .}

P_пр =∑ I² R=I₁ ² R₁ + I₂ ² R₂ =0,96² *24+5,39² *15=457,9 Вт

Q_пр =∑ I² Х=I₁ ² X_L1 -I₂ ² X_C1 -I₃ ² X_C2 =0,96² *104,25–0,96² *3,46–5,39² *10,91= =-224,05 ВAр

S _пр = 457,9 - j 224,05=509,8e^{- j 26,1} BA

510 e ^{– j 26,1°} =509,8e^{- j 26,1°} баланс мощностей соблюдается. Искомые величины верны.

4. Повысить коэффициент мощности до 0,98 включением необходимого реактивного элемента Х. φ=- 26,1 < 0

M(I) = 0,1; φ_x = arccos 0,98 = 11,48; φ = φ_u – φ_i

В данном случаем необходимо добавить индуктивность

L= U /(I_x *ω)

I_x = I₃ *sinφ – I₃ *cosφ*tgφ_x

I_x = 5,1*sin (26,1) – 5,1*cos (26,1)*tg11,48=1,3135A

L= 100 /(1,3135*1256)=60,62 мГн

5. Построение векторных диаграмм токов и напряжений в одной системе координат

U _R1 =I ₁ *R₁ =0,96e^-j76,6 *24=23,04e^-j76,6 В

U _L1 =I ₁ *jX_L1 =0,96 e^-j76,6 *j104,25=[0,96cos (-76,6)+j0,96sin (-76,6)] (j104,25)=

=(0,22-j0,93) (j104,25)=99,63 e^j13,3 В

U _C1 =I ₁ *(-jX_C1 )=0,96 e^-j76,6 *(-j3,46)= [0,96cos (-76,6)+j0,96sin (-76,6)] (-j3,46)=

=3,31 e^j(13,3+180) = 3,31 e^j193,3 В

U _R2 =I ₂ *R₂ =5,39 e^j36 *15=80,85 e^j36 В

U _C2 =I ₂ *(-jX_C2 )=5,39 e^j36 *(-j10,91)=(5,39cos36+5,39sin36) (-j10,91)=

=(4,36+j3,17) (-j10,91)= 58,8 e^{- j 54} В

Масштабы:

М_U =1 В/мм

М_I =0,2 А/мм