ЛЕКЦИЯ №5
МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
СНУ
Пусть дана система вида:
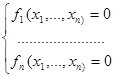 (5.1) (5.1)
f'(x)=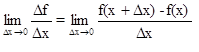 - производная - производная
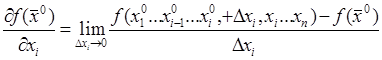
Частная производная 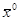 - вектор (все значения). - вектор (все значения).
МЕТОД НЬЮТОНА
Дана система вида (5.1), где fi
один раз непрерывно дифиринцируемые функции, т.е. существуют все частные первые производные этих функций.
Строим последовательность приближений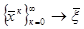 сходящуюся к точному решению системы сходящуюся к точному решению системы 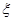 . .
Пусть  - некоторое начальное приближение к решению, а - некоторое начальное приближение к решению, а  - катое приближение к решению. Построим зависимость, позволяющую на основании - катое приближение к решению. Построим зависимость, позволяющую на основании  построить построить  . .
Точное приближение 
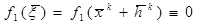
ξ-корень обращает уравнение в верное равенство(тождество).
 (5.2) (5.2)
Разложим функции fi
из системы (5.2) в ряд Тейлора в окрестности точки хк
до линейных составляющих.
 (5.3) (5.3)
Система (5.3) представляет собой систему линейных алгебраических уравнений для поиска компонента вектора поправки hk
.
Перепишем систему (5.3) в виде:
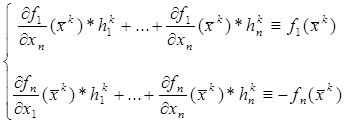 (5.4) (5.4)
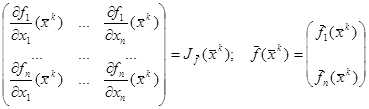
Сокращаем запись системы (5.4) : 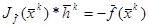 (5.5) (5.5)
Решим систему (5.5) методом обратной матрицы. Определитель Якобиана в точке хк
не равен 0.

Получили связь последующего приближения с предыдущим.
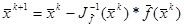 (5.6) (5.6)
 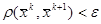 условие окончания вычислений. (5.7) условие окончания вычислений. (5.7)
 - расстояние между векторами (метрика). - расстояние между векторами (метрика).
МЕТОД ИТЕРАЦИЙ
Пусть дана система вида (5.1). Преобразуем ее к виду (5.8) (5.8)
Система (5.8) в векторном виде 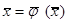 (5.9) (5.9)
Необходимо найти неподвижную точку систему 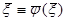
Очевидно, что эта точка ξ – решение системы (5.1)
Пусть дано 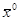 -некоторое начальное приближение к ξ и на k-том шаге получено приближение -некоторое начальное приближение к ξ и на k-том шаге получено приближение  . Тогда последующее приближение : . Тогда последующее приближение :
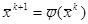 (5.10) (5.10)
Условие окончания совпадает с (5.7)
Всегда ли метод сходится?
Пусть М- матрица, составлена из элементов mij
M=[mij
], где mij
=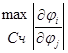
Определение нормы матрицы А: 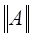 -число удовлетворяющее свойствам. -число удовлетворяющее свойствам.
1) 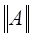 ≥0, ≥0, 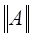 =0 =0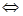 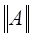 ≡0 ≡0
2)  число число
3) 
4) 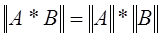
Способы задания нормы матрицы:
1) 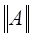 = =
2) 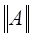 = =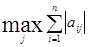
3) 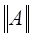 = =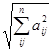
Достаточное условие сходимости метода итераций:
Если 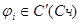 , i=1,n , , i=1,n , 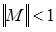 на Сч и на Сч и 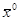 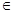 Сч, то процесс итераций сходится независимо от выбора начального приближения. Сч, то процесс итераций сходится независимо от выбора начального приближения.
МЕТОД ЗЕЙДЕЛЯ
Пусть дана система вида (5.1), преобразуем ее к виду (5.8). Как и в методе итераций строим последовательность приближений 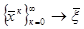 к неподвижной точке. к неподвижной точке.

ускорение сходимости за счет подстановки предыдущего приближения.
Достаточное условие совпадает с достаточными условиями сходимости метода итераций.
Условие окончания получения приближений совпадает с (5.7).
ЛЕКЦИЯ № 6, 7
ПРИБЛИЖЕНИЕ ФУНКЦИИ
Общая постановка задачи.
Пусть ¦(c) – некоторая функция, которая можетбыть известно, частично известной и неизвестной. Эту функцию необходимо заменить некоторой «хорошей» функцией j(c), которая будет достаточно близкой ¦(c).
Постановка задачи интерполяции.
Для того чтобы конкретизировать постановку задачи приближения функции необходимо ответить на следующие вопросы:
1. что известно о ¦(c) (способ задания, степень гладкости);
2. к какому классу, семейству функций должна принадлежать j(c);
3. что понимаем под близостью j(c) и ¦(c) каков критерий согласия;
Часто приближение функции называют аппроксимацией
Постановка задачи интерполяции.
Пусть ¦(c) задана на некотором разбиении отрезка [a;b] точками хi
,
i=0,n , где a = х0
<х1
<…<xn
= b
интерполяция
– вычисление ¦(c) в точке Î[a;b], x¹xi
, i = 0,n
экстраполяция
– вычисление функции ¦(c) в точке ХÎ[a;b];
Определение интерполяции ввел в 1656 году Джон Уолесс, а в 1655 году ввел символ ¥.
Для полиномиальной интерполяции j(c) имеет вид j(c)=а0
+а1
х+а2
х2
+…+аn
xn
.
Для того, чтобы считать j(c) к ¦(c) вводится ограничение j(ci
)= ¦(ci
), i=0,n ;
Т.е значения этих функций в точке хi
должны совпадать. Точки х
i
будем называть узлами интерполяции
Интерполяционный многочлен Лагранжа
Необходимо определить коэффициенты полинома степени n(их будет n+1), построения аппроксимации функции, заданной в n+1 узле. Используя ограничения на j(c): j(ci
)= ¦(ci
)=y, i=0,n , составим систему:
 (6.
1)
(6.
1)
Выпишем определитель этой системы
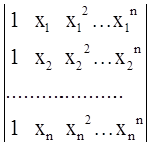
Определитель
Вандермонда
При условии: x0
¹xj
приi¹j определитель системы (6.1) отличен от нуля, следовательно, система имеет единственное решение.
Вывод:
если задано разбиение в виде n+1различной точки, то всегда существует функция в виде полинома n-ой степени, которая проходит через все точки графика ¦(c),определенной на этом разбиении.
Посторонние приближенияфункции при помощи полиномов указанным способом весьма трудоемко и обладает большой вычислительной погрешностью, поэтому его использование для большого числа узлов интерполяции нецелесообразно.
Лагранж предложил строить интерполяционные полиномы в виде:
Pn
(x)=∑ Ci
li
(x) (6.2)
Ci
=
yi
=
¦(ci
), li
(x)=полиномы n-ой степени, которые удовлетворяют условию:
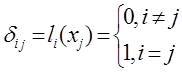
Для полинома узлы интерполяции xj
, j=0,n , j≠I являются корнями, причем действительными и попарно различными (все имеют кратность 1)
Тогда полином li
может быть записан в виде:
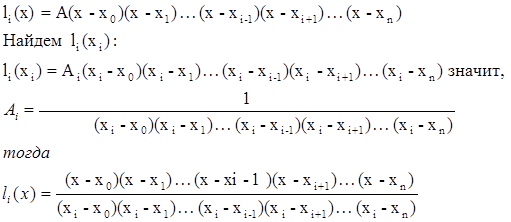 (6.3) (6.3)
Общий вид полинома Лагранжа:
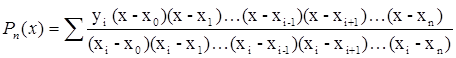 (6.4) (6.4)
Встает вопрос о точности, о приближения функции. Вводится понятие остаточного члена многочлена Лагранжа ; для того, чтобы оценить аппроксимации ¦(c) в некоторой точке xÎ[a;b]
Функцию ¦(c) представим в виде ¦(c)= Pn
(x)+Rn
(x), где Rn
(x)- остаточный член многочлена Лагранжа в процессе длительного и трудоемкого вывода для Rn
(x) получена следующая формула:
 (6.5) (6.5)
Строится система вложенных отрезков
¦(
n
+1)
-производная (n+1)-го порядка
Пусть 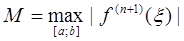
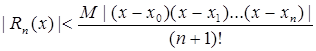 (6.6)
(6.6)
Если ¦(c)-полином n-ой степени, то производная (n+1)-го порядка равна 0, тогда Rn
(x)≡0 и мы получаем точную аппроксимацию.
Теорема:
Многочлен Лагранжа вида (6.4) для таблично заданной функции единственен.
Доказательство:
Пусть Qn
(x)- многочлен Лагранжа, построенный для этой же функции ¦(c) по тем же узлам интерполяции. Qn
(x)¹Pn
(x) Qn
(xi
)=yi
=Pn
(xi
), 
Рассмотрим многочлен Ln
(x)= Qn
(x)-Rn
(x)-это многочлен n-ой степени, для которого точки xi
, i=0,n являются корнями. Это противоречит основной теореме алгебры, которая говорит о том, что полином n-ой степени имеет ровно n корней . А Ln
(x) имеет n+1 корней . Противоречие доказывает теорему.
Интерполяционная схема Эйткина
Поскольку при большом числе узлов интерполяции вычисление значения полинома Лагранжа по формуле (6.4) громоздко, необходимо получить рекуррентную формулу.
Пусть ¦(c)- непрерывна, узлы выбраны на отрезке [a;b] таким образом, что:

Введем функцию 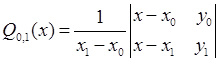
xi
-узлы интерполяции;
yi=
¦(c)
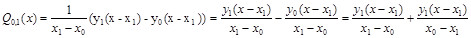
Полином Лагранжа: Pn
(x) см. (6.4)

Таким образом, функция Q0,1
(x) представляет собой полином Лагранжа l-ой степени, построенной по узлам x0
,x1
введем функцию вида
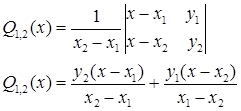
Функция Q1,2
(x)- интерполяционный полином Лагранжа, построенный по узлам x1
,x2
.
Введем теперь функцию

Аналогично:
Q0,1,2
(x2
)= у2
В силу единственности полинома Лагранжа, построенного по узлам x0
, x1
,x2
функция Q0,1,2
(x) представляет собой интерполяционный полином Лагранжа 2-ой степени, построенный по узлам x0
, x1
,x2
.
Введем функцию:
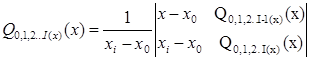 (7.1) (7.1)
Функция представляющая собой полином Лагранжа 2-ой степени, построенного по узлам x0
, x1,…
xi
.
Формула (7.1) позволяет рекуррентно вычислять полином Лагранжа любой степени.
Т.к. (7.1) представляет собой альтернативную форму записи интерполяционного полинома, точность приближения функции также может быть оценена по формуле (6.5)
(7.1)-интерполяционная схема Эйткина.
КОНЕЧНЫЕ РАЗНОСТИ
Пусть функция ¦(c) задана на системе равноотстоящих узлов xi
=x0
+ih, 
где h-шаг сетки, yi
=¦(ci
).
Конечной разностью первого порядка в точке x0
называется ∆y0
=y1
-y0
Конечной разностью первого порядка в точке xi
: ∆yi
=yi
+1
-y0
-yi
Конечной разностью второго порядка в точке x0
: ∆2
y0
=∆y1
-∆y0
Конечной разностью второго порядка в точке xi
: ∆2
yi
=∆yi
+1
-∆yi
Общая формула для конечной разности k-того порядка в точке xi
:
 ∆
k
yi
=∆
k
-1
yi
+1
-∆
k
y
(7.2) ∆
k
yi
=∆
k
-1
yi
+1
-∆
k
y
(7.2)
Заметим: ∆0
yi
=
yi
Формула (7.2) позволяет вычислять рекуррентно конечные разности
Связь конечных разностей и производных
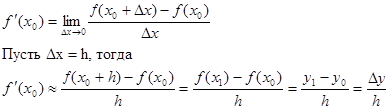
чем меньше h, тем точность выше
Аналогично можем получить связь
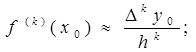 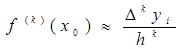 ;
(7.3) ;
(7.3)
Свойства конечных разностей
В связи с производными вида(7.3)конечные разности обладают свойствами:
1. постоянные, равны нулю;
2. постоянный множитель у функции выносится за знак
3. суммы 2-х функций равны сумме каждой функции
4. полинома n-ой степени, n-го порядка постоянны и равны
∆n
y=hn
an
n!
an
-коэффициент при xn
полинома Rn
(x)
Верно и обратное утверждение: все конечные разности n-го порядка некоторой функции постоянны и одинаковы, конечные разности n +1-го порядка равны 0, а конечные разности n-1-го порядка различны, то функция представляет собой полином n-ой степени.
Распространение ошибки в исходных данных
при вычислении конечные разности
Любые измерения несут в себе погрешность (ошибка округления, точность измерения приборов)
Пусть значения функции определены в узлах x0
, 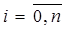 и в некоторой точке xk
значение некоторой точке xk
значение функции найдено с ошибкой ε, т.е ỹk
+ ε и в некоторой точке xk
значение некоторой точке xk
значение функции найдено с ошибкой ε, т.е ỹk
+ ε
Составим таблицу конечных разностей
xk
-2
yk
-2
∆yk
-2
∆2
yk
-2
∆3
yk
-3
+ε
xk
-1
yk
-1
∆yk
-1
+ε∆2
yk
-2
+ε∆3
yk
-2
-3ε
xk
yk
+ε ∆yk
-1
-ε∆2
yk
-1
-2ε∆3
yk
-1
+3ε
xk
+1
yk
+1
∆yk
+1
∆2
yk
+ε ∆3
yk
-ε
xk
+2
yk
+2
∆2
yk
+1
Как видно из таблицы конечных разностей при увеличении порядка конечных разностей ошибка в исходных данных распространяется и растет.
Такое взаимодействие ошибок называют шумом, если это ошибки округлений - то шумом округлений
.
Если ошибки округлений достаточно большие, то может происходить следующее явление: при увеличении порядка конечных разностей они могут уменьшаться и→0, но, дойдя до некоторого малого значения, опять могут начать расти из-за шума округлений.
Столбец в таблице конечных разностей, в которой все конечные разности ≈0, называют «практическим постоянным»; при этом конечные разности высших порядков не используют.
Для интерполяции целесообразно использовать многочлен такой степени, которая совпадает с порядком «практической постоянной» конечных разностей.
ЛЕКЦИЯ №8
ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ДЛЯРАВНООТСТОЯЩИХ УЗЛОВ
Дана функция y=¦(c),заданная на сетке равноотстоящих узлов:
yi
=¦(ci
), xi
=x0
+ihi
, 
Строим интерполяционный полином с целью упрощения записи полинома (интерполяционного) и представления его в виде, позволяющем оценивать влияние каждого из компонентов на значение аппроксимации, запишем его так:
Nn
(x)=-a0
+a1
(x-x0
)+a2
(x-x0
)(x-x1
)+…+an
(x-x0
)…(x-xn-1
) (8.1)
Необходимо посчитать его коэффициенты ai
. Будем находить из условия
Nn
(xi
)=yi

i=0
: Nn
(x0
)=y0
=a0
+a1
0+…+an
0 a0
= y0
i=1
: Nn
(x1
)=y1
= y0
+a1
(x1
-x0
) + a2
0+…+an
0

x1
=x0
+1h=x1
-x0
=h
i=2
: Nn
(x2
)=y2
= y0
+∆y0
/h(x2
-x0
) (x2
-x1
) + a3
0+…+an
0
x2
-x0
=2h
x2
-x1
=h
y2
= y0
+∆y0
2+a2
2h2
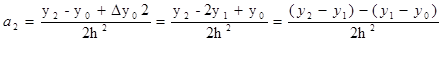
i
=
k
: 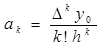 (8.2) (8.2)
Запишем теперь, используя (8.2)
, полином (8.1)
в виде:
Nn
(x)= y0
+∆y0
/h(x-x0
)+…+ ∆n
y0
/n!hn
(x-x0
)(x-x1
)… (x-xn-1
) (8.3)
Полином (8.3)
1-ый интерполяционный многочлен Ньютона. Он наиболее приспособлен для вычисления значения функции в точках, близких к x0
С целью упрощения записи полинома введем переменную 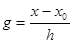
x=x0
+gh
Если g-целое, то будет совпадать с номером узла
x0
– базовый узел полинома (8.3)
xi
=x0
+gh- x0
-ih=h(g-i);
Nn
(g)= y0
+∆y0
g+…+ ∆n
y0
/n!g(g-1)(g-2)(g-n+1) (8.4)
Полином Ньютона в силу единственности существования интерполяционного полинома Лагранжа является одной из форм записи полинома Лагранжа, поэтому для полинома (8.3) справедливо, что формула остаточного члена полинома Лагранжа

Для вычисления функции в точках находящихся в середине сетки узлов интерполяции либо в ее конце, т. е близкие к xn
, применяют два подхода
1. строят формулы для вычисления функции в точках х, близких к середине сетки интерполяции
2. формулы для точек х, близких к хn
(упорядочивание узлов интерполяции).
Соответственно получаются формулы Стирлинга , Бесселя, Гаусса, и 2-ой интерполяционный многочлен Ньютона .
Второй путь: в качестве узла х0
для заданной точки х берут тот узел, который наиболее близок к х, узел х1
выбирают как самый близкий из оставшихся узлов к х.
Т.е последовательность  упорядочившаяся по возрастанию. упорядочившаяся по возрастанию.
Для вычисления значения функции в точке х используется 1-ый интерполяционный многочлен Ньютона.
х0 х1 х2 х3 х4 х5 х6
Преобразуем узлы:
х0
′=x3;
x1
′=x4
;
x2
′=x2
;
x3
′=x5
;
Разделенные разности
Пусть функция ¦(c),задана на системе неравно отстоящих узлов.
Разделенной разностью 1-го порядка назовем выражение:
 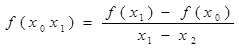
Разделенной разностью 2-го порядка:
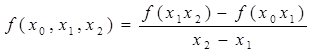
Разделенной разностью k-го порядка:
 (8.6) (8.6)
|x-x0
|, 
Свойства разделенной разности:
- на сетке равноотстоящих узлов разделенной разности совпадают конечными разностями
- разделенные разности понижают степень многочлена
- разделенные разности n-го порядка постоянны и равны
Интерполяционная формула Ньютона для не равноотстоящих узлов
Пусть функция ¦(c), задана на сетке не равноотстоящих узлов xi
,  .Запишем следующие разделенные разности: .Запишем следующие разделенные разности:
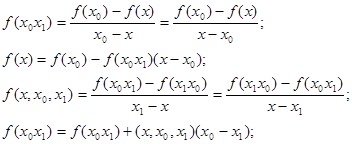
Выполним такие действия n-1 раз, получим:
 Полином Ньютона: Полином Ньютона:
Nn
(x)=¦0
(c)
Rn
(x)= ¦(c,c0,…
cn
)(x-x0
)… (x-xn
) (8.8)
То¦(c)= Nn
(x)+ Rn
(x)
Nn
(x) ≈ ¦(c)
Rn
(x) = ¦(c) - Nn
(x)
Если ¦(c) имеет (n+1)-ую производную, то остаточный член может быть преобразован к виду остаточного члена (8.9)
полинома Лагранжа.
При вычислении полинома в точке х узлы интерполяции лучше переименовать так, чтобы х0
был самым близким к х, а все остальные узлы тем более удаленные по увеличению расстояния к х.
|