Содержание
Введение
1. Продольное обтекание тел вращения
2. Поперечное обтекание тел вращения
3. Продольное и поперечное обтекание удлиненных тел вращения
4. Применение метода особенностей для расчета продольного и поперечного обтеканий тел вращения
Список источников
Введение
Теоретическая механика, изучая простейшие, механические формы движения и взаимодействия материальных тел, отвлекается от многих их действительных свойств и использует в качестве допустимой абстракции понятия материальной точки и системы материальных точек. Материальная система может быть как дискретной, состоящей из отдельных материальных точек, так и сплошной, представляющей непрерывные распределения вещества и физических характеристик его состояния и движения в пространстве. В этом случае систему называют сплошной материальной средой или, короче, сплошной средой.
Простейшим примером сплошной среды является неизменяемая среда или абсолютно твердое тело. Более общий образ изменяемой сплошной среды объединяет в механике как упругие и пластические, так и жидкие и газообразные тела.
Раздел теоретической механики, занимающийся движениями такого рода изменяемых сред, носит наименование механики сплошных сред, а часть ее, относящаяся к жидким и газообразным средам, – механики жидкости и газа. Этот термин получил в последнее время широкое распространение, придя на смену ранее употреблявшемуся термину гидромеханика, включавшему в себя как собственно механику жидкости (от греческого «хидрос» – вода), так и механику газов, в частности воздуха. Развитие авиации вызвало особый интерес к вопросам силового взаимодействия воздуха с движущимися в нем телами (теория крыла и винта) и движения тел в воздухе при наличии этих взаимодействий (динамика полета); так появилась аэромеханика. Углубление знаний в области движения сжимаемых жидкостей (газов) привело к возникновению газовой динамики, а применение ее результатов к авиации и ракетной технике положило основание к созданию новой дисциплины – аэротермодинамики, под которой сейчас понимают механику и термодинамику газа, движущегося с большими сверхзвуковыми и гиперзвуковыми скоростями.
Современный этап развития механики жидкости и газа, так же как и вообще механики сплошной среды, характеризуется значительно возросшей вязью с физикой. Требования главным образом ракетной техники поставили перед механикой жидкости и газа новые задачи, определяемые, с одной стороны, гиперзвуковыми (космическими) скоростями движения тел сквозь атмосферу в широком диапазоне высот, с другой – движениями газов в камерах горения и соплах двигателей. В этих условиях приходится иметь дело со сверхвысокими температурами, вызывающими диссоциацию и ионизацию газа, явлениями, связанными с разреженностью атмосферы на больших высотах полета, с разрушением (плавлением и испарением) твердой поверхности обтекаемого газом тела, излучением тепла поверхностью тела и самим газом, с движениями смесей реагирующих между собой газов (например, при горении) и многими другими физическими и химическими процессами. При использовании потоков ионизированного газа (плазмы) для непосредственного превращения тепла в электрическую энергию в магнитогидродинамическом генераторе необходимо рассматривать взаимодействие движущегося газа не только с твердыми телами, но и с электрическими и магнитными полями (магнитная гидродинамика). Все сказанное о газе относится, хотя и в несколько меньшей степени, и к жидкостям. В настоящее время жидкости широко используются как носители тепла в атомной энергетике; процессы тепломассопереноса в жидкостях лежат в основе многих главным образом химических производств, металлургия с успехом применяет магнитную гидродинамику для управления потоками жидких металлов в процессах плавки и др.
Вот почему предмет механики жидкости и газа сейчас уже нельзя сводить к одному механическому движению жидкости и газа и механическому взаимодействию их с твердыми телами. Механические движения сопровождаются общими движениями материи – сложными физическими процессами, которыми не только нельзя пренебрегать, как это делалось ранее, а наоборот, следует иметь в виду, что эти процессы во многих практических задачах играют главную роль, оставляя механическим движениям вспомогательное, подчиненное значение.
Кроме уже упомянутого ранее основного свойства принятой модели жидкой и газообразной среды – ее сплошности (непрерывности распределения массы и физико-механических характеристик среды), для динамики существенно второе основное свойство жидкой или газообразной среды – ее легкая подвижность, или текучесть, – выражающееся в том, что для большинства жидкостей и всех газов касательные напряжения (внутреннее трение) в среде отличны от нуля только при наличии относительного движения сдвига между слоями среды. При относительном покое внутреннее трение отсутствует. В этом заключается отличие жидкой или газообразной среды, например, от упругой среды, в которой касательные напряжения, обусловленные наличием деформаций (а не скоростей деформаций) сдвига, отличны от нуля и при относительном покое среды.
Обладая общими свойствами непрерывности и легкой подвижности, жидкости и газы отличаются друг от друга по физическим свойствам, связанным с различием во внутренней их молекулярной структуре.
Предполагая отсутствие внутреннего трения и процессов переноса, приходят к модели идеальной жидкости, которая оказывается пригодной для описания многих важных сторон явлений обтекания тел, но по самой своей сущности не может, например, объяснить происхождения сопротивления тел, разогревания жидкостей и газов за счет диссипации механической энергии в тепло, тепломассопереноса в жидкости и др. Для описания этих явлений необходимо пользоваться более сложной моделью вязкой, проводящей тепло и обладающей способностью переноса примесей (диффузии) жидкости или газа.
1. Продольное обтекание тел вращения
Для расчета внешнего осесимметричного обтекания тел вращения (см. Приложение 1) возьмем в меридианальных плоскостях (r, x)
эллиптическуюсистему координат (
x
,
h
)
, связанную с (r, x)
соотношениями
х =
с ch x cos h, 0 £x£¥,
r = с shxsinh, 0 £h£ 2p,
где величина c
представляет расстояние фокусов семейства координатных линий – сoфокусных эллипсов и гипербол – от начала координат.
Положим
ch x = l, cos h =
m, l £l£¥, -1 £m£ 1;
тогда связь между координатами (r, x)
и (
l
,
m
)
будет иметь вид
х = сlm, r = с Öl2
– 1 Ö 1 – m2
. (1)
Определив производные
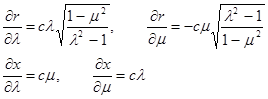
найдем коэффициенты Ламе[1]
 (2) (2)
После этого уже нетрудно составить и основное дифференциальное уравнение Лапласа для потенциала скоростей. Согласно формуле[2]
 (*) (*)
получим 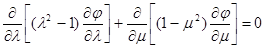 (3) (3)
Будем искать частное решение этого уравнения в виде произведения двух функций от переменных l и m в отдельности
j
= L(
l
) M(
m
)
; (4)
тогда в уравнении (2) переменные разделятся и из равенства
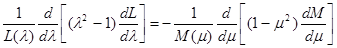
в силу независимости l и m будет следовать, что каждая из частей равенства должна быть постоянной. Полагая эту постоянную равной n (n+1)
, где n
– целое положительное число, получим для определения L(l) и М(m) два обыкновенных линейных уравнения второго порядка лежандрова типа
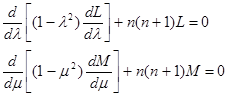 (5) (5)
Этим уравнениям удовлетворяют[3]
два класса независимых решений:
1) функции Лежандра 1-го рода – полиномы Лежандра Pn
(х)
, определяемые равенствами
2)
P0
(x) = 1, Р1
(х) = х, P2
(x) = 0.5 (Зх2
-1), P3
(x) = 0.5 (5x3
-3x),…
и рекуррентным соотношением для вычисления последующих полиномов
(n + 1) Pn +1
(х) = (2n + 1) хРn
(х) – nРn-1
(х);
2) функции Лежандра 2-го рода Qn
(х)
, определяемые равенствами
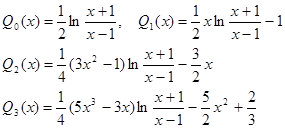
и рекуррентным соотношением
(n + 1) Qn+1
(х) = (2n + 1) xQn
(х) – nQn-1
(х),
совпадающим с предыдущим соотношением для полиномов Лежандра.
Представим решение уравнения (3) как сумму двух потенциалов: 1) потенциала j¥
однородного потока, набегающего на тело со скоростью U
¥
; этот потенциал по первой из формул (1) будет равенj
¥
= U
¥
x = U
¥
c
l
m
.
и 2) потенциала j' скоростей возмущений, который выразим суммой частных решений (4).
Функция Pn
(х)
, как полином n
-й степени, обращается в бесконечность при бесконечно возрастающем аргументе, функция же Qn
(х)
при этом стремится к нулю, но зато логарифмически бесконечна при х = ± 1
. В случае внешнего обтекания тела координата l = ch x может достигать бесконечных значений, а координата m ограничена. Примем во внимание, что потенциал скоростей возмущенного движения (т.е. обтекания за вычетом однородного потока со скоростью, равной скорости на бесконечности) должен стремиться к нулю при удалении от поверхности тела, причем 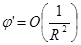 . .
Из приведенных соображений следует, что искомые частные решения должны иметь вид произведений Qn
(
l
) Pn
(
m
)
(n = 1, 2,…);
подчеркнем, отсчет n
при суммировании начинается с единицы, а не с нуля. Это подтверждается наличием следующих очевидных асимптотических равенств, справедливых при больших значениях l, а, следовательно, согласно (1), и R = =
Ö
х2
+ r2
, имеющего тот же порядок, что иl:
 
Таким образом, будем иметь правильный порядок убывания j' на бесконечности, если положим
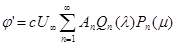 ,
(6)
,
(6)
где An
- постоянные коэффициенты, зависящие от формы поверхности тела.
Складывая потенциалы j¥
и j', получим искомый потенциал скоростей продольного обтекания тела вращения со скоростью на бесконечности, равной U
¥
,
 (7) (7)
Для определения коэффициентов An
найдем выражение функции тока y. По формуле (2) будем иметь

или после подстановки разложения (7)
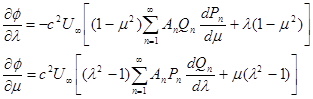
Переписывая второе равенство в виде

подставим под знак суммы выражение для Pn
из основного дифференциального уравнения функций Лежандра (5)

Тогда будем иметь

Интегрируя по m и добавляя необходимую функцию от l, получим окончательное выражение для функции тока
 (8) (8)
Уравнение нулевой
поверхности тока будет
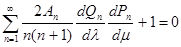 (9) (9)
Сравнивая его с заданным уравнением профиля тела вращения в эллиптических координатах, можно определить величины коэффициентов Аn
, что и решает задачу. Конечно, именно этот пункт и является наиболее сложным с вычислительной стороны.

Имея выражение потенциала скоростей, найдем скорость по формуле (10).
2. Поперечное обтекание тел вращения
Наряду с продольным обтеканием тел вращения представляет интерес и поперечное обтекание, перпендикулярное (Приложение 1, б) к оси симметрии тела. Из сложения этих двух потоков можно получить обтекание тела вращения под любым углом
.
В этом случае уже не получается осесимметричного движения. Уравнение Лапласа, определяющее потенциал скоростей, будет в ортогональной системе криволинейных координат, согласно (*), иметь вид

Сохраняя ту же систему координат (l, m, e), что и в случае осесимметричного обтекания тела вращения, и используя выражения коэффициентов Ламе (2), перепишем предыдущее уравнение в форме
 (13) (13)
Будем искать решение этого уравнения в виде произведения двух функций
j
= N(
l
,
m
) Е(
e
);
тогда, подставляя последнее выражение в уравнение (13) и разделяя функции независимых переменных, получим систему уравнений (k –
произвольное число, которое будем считать положительным и целым)

Первое уравнение имеет решение: Е = A cos k
e
+ В sin k
e
;
второе, если положить N = L(
l
) М(
m
)
и разделить переменные, может быть приведено к системе уравнений

имеющей в качестве частных решений так называемые присоединенные функцииЛежандра[4]
 (14) (14)
Комбинируя эти функции так, чтобы выражение потенциала скоростей возмущенного движения было ограниченным при l®¥, получим общее выражение потенциала скоростей
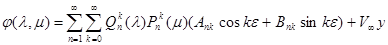
здесь последнее слагаемое представляет собой потенциал скоростей набегающего на тело однородного потока со скоростью на бесконечности V
¥
, направленной параллельно оси Оу
(Приложение 1, б).
Полагая в только что выведенной общей формуле потенциала
An1
=
с
V
¥
С
n
, An2
= An3
=…
= 0, Bn1
= Вn2
=… = 0,
т.е. довольствуясь решением, содержащим cos e, и, кроме того, представляя у
по формулам, помещенным в начале § 1, как функцию l, m и e
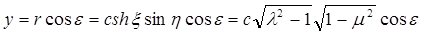
получим следующее выражение потенциала скоростей поперечно набегающего со скоростью V
¥
вдоль оси Оу
потока:
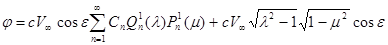
или, используя определение присоединенных функций Лежандра (14),
 (15) (15)
Для определения постоянных Сn
, как и ранее, следует составить граничное условие на заданной поверхности обтекаемого тела. В этом случае неосесимметричного движения функция тока отсутствует и приходится непосредственно вычислять нормальную скорость Vn
=
¶
j
/
¶
n
и приравнивать ее нулю.
Несколько облегчая вычисления, выпишу в выбранной системе координат (l, m) условие, что при непроницаемости поверхности обтекаемого тела элемент дуги его меридианного сечения параллелен составляющей скорости в меридианной плоскости (условие скольжения жидкости по поверхности тела):
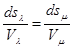
или, вспоминая выражения элементов дуг координатных линий и проекций градиента потенциала на направления этих линий,

Отсюда вытекает искомое граничное условие
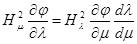 (16) (16)
в котором l является заданной функцией m согласно уравнению контура обтекаемого тела в меридиональной плоскости. Составляя частные производные ¶
j
/
¶
l
,
¶
j
/
¶
m
и используя (15) получаю:
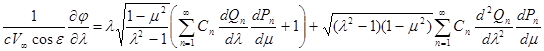
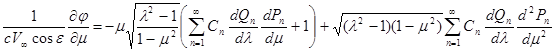
Заменив входящие сюда выражения вторых производных на основании дифференциальных уравнений функций Рn
и Qn
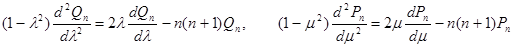
получим после простых приведений
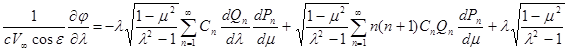
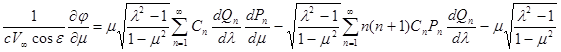
Подставляя эти выражения производных в (16) и используя ранее выведенные значения коэффициентов Ламе

получим после очевидных сокращений
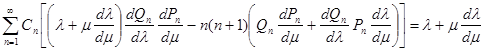
Имея в виду, что на поверхности тела l представляет заданную функцию от m, перепишем граничное условие в окончательной форме так:
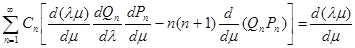 (17) (17)
3.Продольное и поперечное обтекание удлиненных тел вращения
В большинстве практических приложений приходится иметь дело с телами вращения, удлинение которых, т.е. отношение длины к максимальной толщине, довольно велико (порядка 8–12). Это объясняется хорошей обтекаемостью такого рода тел реальной жидкостью.
Расчет обтекания тел вращения большого удлинения может быть произведен приближенным методом. Изложим его основную идею[5]
.
Основным затруднением в решении задачи является определение коэффициентов Аn
при продольном и Сn
– при поперечном обтекании тела. Чем проще будет связь между l и m, определяющая форму контура в меридианной плоскости, тем меньше коэффициентов Аn
, Сn
можно брать в разложениях потенциала скоростей. Самая простая связь представляется равенством l = const, т.е. случаем обтекания эллипсоида. Отсюда следует вывод: чем ближе исследуемое тело по форме к эллипсоиду, тем легче может быть разрешена задача. В связи с этим решим, прежде всего, вопрос о выборе положения начала координат на продольной оси тела. Замечу, что фокусы удлиненного эллипсоида вращения находятся посередине отрезка, соединяющего точки пересечения большой оси и поверхности эллипсоида с центром кривизны поверхности в этих точках. Начало координат следует выбирать совпадающим с серединой отрезка, соединяющего фокусы; при таком выборе начала координат, чем ближе обтекаемое тело к эллипсоиду, тем меньше уравнение контура будет отличаться от простейшего равенства l = const.
Если обтекаемое тело имеет большое удлинение, то поверхность его располагается в области значений l, мало превышающих значение l = сhx = 1 или x = 0, соответствующее отрезку оси Oz
, соединяющему фокусы. Рассматривая значения функций Qn
(
l
)
и dQn
/d
l
при l, лишь немного превышающих единицу, убедимся, что при достаточно малых x будут иметь
место равенства
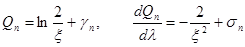 (18) (18)
где gn
и dn
– малые по сравнению с первыми членами поправки. Замечательно, что согласно равенствам (18), при малых x все функции Qn
и dQn
/d
l
в первом приближении не зависят от индекса n.
Основное граничное условие продольного обтекания (9) в первом приближении будет, согласно (18), иметь вид
 (19) (19)
где производная dPn
/d
m
представляет известную функцию величины m = cos h. Ограничивая сумму некоторым фиксированным числом членов n = m
, можно, пользуясь выражениями полиномов Лежандра (из § 1), написать тождество
 (20) (20)
из которого можно вывести выражения коэффициентов An
через an
. Так, например, приm = 5
имеем
A1
= a1
– 3/5 a3
+ 3/35 a5
, A2
= a2
– 9/7 a4
, A3
= 8/5 a3
– 32/15 a5
,
A
4
= 16/7
a
4
,
A
5
= 64/21
a
5
.
Представив контур меридианного сечения приближенным тригонометрическим разложением в эллиптических координатах
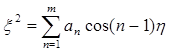 (21) (21)
определим тем самым числа аn
, а уже после этого, согласно тождеству (20), и величины коэффициентов An
, что и дает первое приближение к решению задачи об осесимметричном продольном обтекании удлиненного тела вращения. Если удлинение обтекаемого тела велико, то указанное приближение оказывается для практики достаточным. При желании можно учесть в формулах (18) остаточные члены gn
и dn
, что приведет ко второму и следующим приближениям.
Аналогичным путем решается вопрос о поперечном обтекании удлиненного тела вращения. При плавности контура l изменяется в пределах от 1 + ½ x2
min
до 1 + ½ x2
max
; при этом m остается в пределах ±1. Таким образом, можно считать, что производная d
l
/d
m
имеет порядок x2
max
, т.е. сравнительно мала. Отсюда следует, что величина

имеет порядок единицы. Рассматривая граничное условие (17) видим, что стоящая в квадратной скобке слева величина

мала по сравнению с величиной  . Действительно, . Действительно,
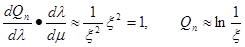
Таким образом, в квадратной скобке в левой части равенства (*) первый одночлен имеет при малых x порядок 1/x2
, второй – ln 1/x.
Из приведенного рассуждения следует, что на поверхности удлиненного тела вращения, где x мало, точное граничное условие поперечного обтекания (17) может быть заменено на приближенное
 (22) (22)
Сравнивая это граничное условие с приближенным граничным условием продольного обтекания (19), видим, что между искомыми коэффициентами An
и Cn
существует простое соотношение
Cn
= -2
An
/
n
(
n
+1).
(23)
В первом приближении обе задачи – продольного и поперечного обтекания – решаются одновременно и сравнительно легким путем. При обычных значительных удлинениях тел вращения вполне можно довольствоваться первым приближением.
Определив коэффициенты An
и Cn
, найду выражения потенциалов и компонент скоростей для продольного и поперечного обтеканий, после чего уже нетрудно разыскать и распределение скоростей и давлений по поверхности заданного тела вращения или вне его при любом угле. Отмечу, что при всех вычислениях на поверхности удлиненного тела и вблизи нее можно пользоваться для Qn
и dQn
/d
l
приближенными выражениями (18). Само собой разумеется, что при удалении от поверхности обтекаемого тела l возрастает и формулы (18) становятся все менее и менее точными.
4.
Применение метода особенностей для расчета продольного и поперечного обтеканий тел вращения
Изложенный в предыдущих параграфах (§ 1 и § 2) метод исследования продольного и поперечного обтеканий тел вращения, основанный на непосредственном решении уравнения Лапласа в эллиптических координатах, не является единственным методом решения этой задачи. Первоначально формы обтекаемых тел вращения для дирижаблей определялись наложением однородного, параллельного некоторой оси потока на поток от системы источников (стоков), распределенных вдоль той же оси. Для этой цели применялись вначале дискретные особенности потока – системы источников (стоков) или диполей, а впоследствии – непрерывные их распределения.
Предположим для определенности, что на отрезке (– с, + с)
оси Ох
задано непрерывное распределение источников (стоков) интенсивности q(х).
Тогда потенциал j' возмущенного движения, созданного этой системой особенностей, будет равен (знак минус введем в определение интенсивности q
)
 (24) (24)
Если задаться видом функции q(x')
, то, вычисляя интеграл (24), получим потенциал скоростей, а дифференцирование по r
и x
позволит вычислить и проекции скорости Vr
и Vx
. Наоборот, задаваясь формой обтекаемого тела, можно, переходя от потенциала скоростей возмущенного движения к полному потенциалу продольного обтекания тела однородным потоком с заданной скоростью на бесконечности и написав условие непроницаемости поверхности тела, получить интегральное уравнение, в котором q(х')
будет неизвестной функцией. Заменяя потенциал скоростей на функцию тока, Карман[6]
разработал метод приближенного интегрирования соответствующего интегрального уравнения, основанный на замене интеграла конечной суммой. Однако метод Кармана не был достаточно общим и, кроме того, требовал решения в каждом отдельном случае системы большого числа линейных алгебраических уравнений, что делало его на практике слишком трудоемким.
Аналогично, пользуясь выражением потенциала диполя: – m cos
q
/ (4
p
r2)
, можно составить и потенциал j¢ поперечного обтекания тела вращения, складывая потенциал однородного натекания с заданной скоростью на бесконечности с потенциалом скоростей возмущенного движения жидкости от непрерывно распределенных по отрезку – с < х < с
диполей интенсивности m(х')
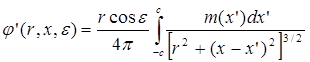 (25) (25)
Здесь также можно задаваться распределением интенсивности m (х')
или, наоборот, определять эту интенсивность из интегрального уравнения, представляющего условие непроницаемости заданной поверхности тела по отношению к потоку, складывающемуся из возмущенного и однородного на бесконечности.
Не останавливаясь на изложении этих в настоящее время уже малоупотребительных методов, укажем лишь на простую их связь с методами, изложенными в предыдущих параграфах. Покажем, что при заданной форме поверхностей обтекаемых тел вращения неизвестные функции q(х')
и m(х')
могут быть выражены через ранее введенные коэффициенты An
и Сn
.
Разобьем ось симметрии тела вращения Ох
на две области: одну, определяемую интервалом – с
£
х
£
с
, заполненным особенностями, и вторую, представляющую остальную часть оси Ох
, где | x | > c.
В эллиптических координатах l, m отрезок, на котором расположены особенности, можно представить, согласно формуле r = c
Ö
l
2
– 1
Ö
1 –
m
2
, так:
l
= 1, – 1
£
m
£
1,
а остальную часть оси Ох
, как
m
= ±1, 1 <
l
<
¥
.
Тогда, сравнивая между собой вне отрезка (– с <
х' <
с)
выражения потенциалов возмущений (24) и (25) с соответственными выражениями тех же потенциалов и приняв во внимание, что Рn
(1) = 1
, получим следующие два равенства:
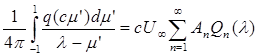 (26) (26)
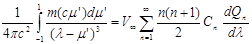 (27) (27)
которые при заданных коэффициентах An
и Сn
можно рассматривать как два интегральных уравнения для определения неизвестных функций q
и m.
Интегральное уравнение (26) может быть решено, если искать решение в виде ряда 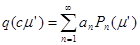 , – 1
£
m'
£ 1.
Подставляя это разложение в (26), получим , – 1
£
m'
£ 1.
Подставляя это разложение в (26), получим
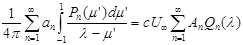
Замечая, что по известной формуле теории функций Лежандра[7]

перепишем предыдущее интегральное уравнение в виде
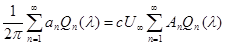
откуда будет сразу следовать искомое решение
an
= 2
p
cU
¥
An
, 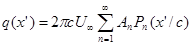 (28) (28)
Для разыскания второй неизвестной функции m(х')
продифференцируем раз по l и другой раз по m' известное разложение[8]
 
тогда получим
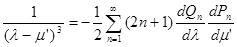
Подставляя это разложение в интегральное уравнение (27), преобразуем его к виду
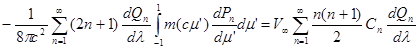
Используя далее разложение неизвестной функции m (c
m
¢
)
в форме

и замечая, что в силу ортогональности полиномов Лежандра

убедимся в справедливости равенства cn
= Сn
.
Итак, имеем
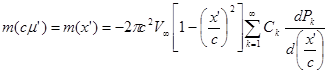 (29) (29)
Совокупности формул (24) и (28), (25) и (29) позволяют при желании пользоваться потенциалами скоростей возмущений в цилиндрических координатах, если уже заранее вычислены коэффициенты An
и Сn
. Замечу, что эти коэффициенты проще определять при помощи разложений уравнения контура меридианного сечения в ряды по функциям от эллиптических координат, а уже затем проводить расчеты в эллиптических или цилиндрических координатах. Как было показано в предыдущем параграфе, в случае удлиненных тел коэффициенты An
и Сn
легко определяются путем разложения уравнения контура в тригонометрический ряд по косинусам эллиптической координаты h.
Замечу еще в заключение, что для тел с очень большим удлинением можно определить q(х)
и m(х)
из следующих двух простейших предположений:
1) в случае продольного обтекания считать нормальную к поверхности тела составляющую скорости возмущения V
¢
n
равной скорости плоского движения от источника, расположенного в ближайшей точке оси. Тогда условие непроницаемости поверхности даст
V
¢
n
=
q
(
x
) / 2
p
r
=
U
¥
dr
/
dx
,
откуда
q
(
x
) = 2
p
U
¥
r
dr
/
dx
=
U
¥
dA
/
dx
, (30)
причем r(x)
представляет заданное уравнение контура меридианного сечения, A
– площадь поперечного сечения;
2) в случае поперечного обтекания тела вращения выберем m(x)
из условия, чтобы элемент тела, вырезанный плоскостями х
и х + dx
, обтекался так же, как элемент цилиндра бесконечного размаха в плоском движении. Это приведет к равенству
m(х) = 2
p
V
¥
r2
(х) = 2V
¥
A(х).
(31)
Список использованных источников
1. Лойцянский Л.Г., Механика жидкости и газа, Главная редакция физико-математической литературы издательства «Наука», М., 1987 г.
2. Е. Уиттекер и Г. Ватсон, Курс современного анализа
3. Я.М. Серебрийский, Обтекание тел вращения, т. VIII
4. Н.Я. Фабрикант, Курс аэродинамики, ч. I
5. И.А. Кибель, Н.Е. Кочин и Н.В. Розе, Теоретическая гидромеханика, ч. I
6. Г. Ламб, Гидродинамика.
[1]
Е. Уиттекер и Г. Ватсон, Курс современного анализа, ч. II, стр. 85
[2]
Лойцянский Л.Г., Механика жидкости и газа, Главная редакция физико-математической литературы издательства «Наука», М., 1987 г.
[3]
Е. Уиттекер и Г. Ватсон, Курс современного анализа, ч. II, с. 91
[4]
Е. Уиттекер и Г. Ватсон, Курс современного анализа, ч. II, стр. 119.
[5]
Я.М. Серебрийский, Обтекание тел вращения, т. VIII.
[6]
Н.Я. Фабрикант, Курс аэродинамики, ч. I, гл. III.
[7]
Уиттекер и Ватсон, Курс современного анализа, ч. II, с. 114
[8]
Уиттекер и Ватсон, Курс современного анализа, ч. II, стр. 117.
|