Нижегородский государственный технический университет
Павловский филиал
Кафедра «Общеобразовательные и общепрофессиональные дисциплины»
КУРСОВАЯ РАБОТА
по информатике
на тему:
«Решение дифференциальных уравнений. Обзор»
Выполнила: Аверина Л.А
Группа. ТМв 151001-09
Проверила: Ловыгина М.Б
Павлово 2010г.
Оглавление
Введение
1 Обзор методов решения в Excel
1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка
1.2 Задача Коши
1.3 Метод Эйлера
1.4 Модифицированный метод Эйлера
1.5 Практическая часть
2 Решение дифференциальных уравнений с помощью Mathcad
2.1 Метод Эйлера
2.2 Метод Эйлера с шагом h/2
2.3 Метод Рунге – Кутты
Заключение
Список литературы
Уравнение  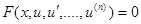 называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области  и, во всяком случае, зависит от и, во всяком случае, зависит от 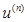 . Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид . Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид 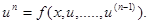
Решением этого уравнения на интервале I=[a,b] называется функция u(x).
Решить дифференциальное уравнение у/
=f(x,y) численным методом - это значит для заданной последовательности аргументов х0
, х1
…, хn
и числа у0
, не определяя функцию у=F(x), найти такие значения у1
, у2
,…, уn
, что уi
=F(xi
)(i=1,2,…, n) и F(x0
)=y0
.
Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk
-xk
-1
называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)
1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка
Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y' = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:
yk+1 = yk +(k1 +2k2 +2k3 +k4 )/6, (2)
где
k1
= Fk h = F(xk , yk )h
k2
= F(xk +h/2, yk +k1
/2)h
k3
= F(xk +h/2, yk +k2
/2)h
k4
= F(xk +h, yk +k3
)h,
k = 0, ..., n-1
h = (xf -x0
)/n (3)
1.2 Задача Коши
Рассмотрим задачу Коши для уравнений первого порядка на отрезке [a,b]:
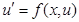 , , 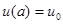 (4) (4)
Разобьём промежуток [a,b] на N частей 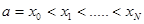 . Обозначим , где u(x) –точное решение задачи Коши, и через . Обозначим , где u(x) –точное решение задачи Коши, и через  значения приближенного решения в точках значения приближенного решения в точках 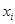 . Существует 2 типа численных схем : . Существует 2 типа численных схем :
1. явные:  ) (5) ) (5)
2. неявные:  (6) (6)
Здесь F некоторая функция, связывающая приближения. В явных схемах приближенное значение  в точке в точке 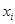 определяется через некоторое число k уже определённых приближенных значений. В неявных схемах определяется через некоторое число k уже определённых приближенных значений. В неявных схемах  определяется не рекурентным способом, как в явных схемах, а для его определения возникает уравнение, поскольку равенство (6) представляет из себя именно уравнение на определяется не рекурентным способом, как в явных схемах, а для его определения возникает уравнение, поскольку равенство (6) представляет из себя именно уравнение на  . Явные схемы проще, однако зачастую неявные схемы предпочтительнее . Явные схемы проще, однако зачастую неявные схемы предпочтительнее
1.3 Метод Эйлера
Решить дифференциальное уравнение у/
=f(x,y) численным методом - это значит для заданной последовательности аргументов х0
, х1
…, хn
и числа у0
, не определяя функцию у=F(x), найти такие значения у1
, у2
,…, уn
, что
уi
=F(xi
)(i=1,2,…, n) и F(x0
)=y0
. (7)
Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk
-xk
-1
называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Рассмотрим дифференциальное уравнение первого порядка (7) с начальным условием
x=x0
, y(x0
)=y0
(8)
Требуется найти решение уравнения (7) на отрезке [а,b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х0
, х1
, х2
,…, хn
, где xi
=x0
+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(хi
)»yi
вычисляются последовательно по формулам уi
+hf(xi
, yi
) (i=0,1,2…).
При этом искомая интегральная кривая у=у(х), проходящая через точку М0
(х0
, у0
), заменяется ломаной М0
М1
М2
… с вершинами Мi
(xi
, yi
) (i=0,1,2,…); каждое звено Мi
Mi
+1
этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (7), которая проходит через точку Мi
. Если правая часть уравнения (7) в некотором прямоугольнике R{|x-x0
|£a, |y-y0
|£b}удовлетворяет условиям:
|f(x, y1
)- f(x, y2
)| £ N|y1
-y2
| (N=const), (9)
|df/dx|=|df/dx+f(df/dy)| £ M (M=const),
то имеет место следующая оценка погрешности:
|y(xn
)-yn
| £hM/2N[(1+hN)n
-1], (10)
где у(хn
)-значение точного решения уравнения (7) при х=хn
, а уn
- приближенное значение, полученное на n-ом шаге.
Формула (13) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2. Погрешность более точного значения уn
*
оценивается формулой
|yn
-y(xn
)|»|yn
*
-yn
|. (11)
Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.
1.4 Модифицированный метод Эйлера
Рассмотрим дифференциальное уравнение (7) y/
=f(x,y) с начальным условием y(x0
)=y0
. Разобьем наш участок интегрирования на n равных частей. На малом участ интегральную кривую заменим прямой линией.

Рисунок 1 Метод Эйлера в графическом виде
Получаем точку Мк
(хк
,ук
). Через Мк
проводим касательную:
у=ук
=f(xk
,yk
)(x-xk
)
Делим отрезок (хк
,хк1
) пополам
xNk
/
=xk
+h/2=xk
+1/2
(12)
yNk
/
=yk
+f(xk
,yk
)h/2=yk
+yk
+1/2
Получаем точку Nk
/
. В этой точке строим следующую касательную:
y(xk
+1/2
)=f(xk
+1/2
, yk
+1/2
)=αk
(13)
Из точки Мк
проводим прямую с угловым коэффициентом αк
и определяем точку пересечения этой прямой с прямой Хк1
. Получаем точку Мк
/
. В качестве ук+1
принимаем ординату точки Мк
/
. Тогда:
ук+1
=ук
+αк
h
xk
+1
=xk
+h
αk
=f(xk
+
h
/2
, yk
+f(xk
,Yk
)h/2) (14)
yk
=yk-1
+f(xk-1
,yk-1
)h (14)
(14)-рекурентные формулы метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции ук+1/2
в точках хк+1/2
, затем находят значение правой части уравнения (11) в средней точке y/
k
+1/2
=f(xk
+1/2
, yk
+1/2
) и определяют ук+1
.
Для оценки погрешности в точке хк
проводят вычисления ук
с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений:
| ук
*
-у(хк
)|=1/3(yk
*
-yk
), (15)
где у(х)-точное решение дифференциального уравнения.
Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y//
=f(y/
,y,x) c начальными условиями y/
(x0
)=y/
0
, y(x0
)=y0
, выполняется замена
y/
=z (16)
z/
=f(x,y,z)
Тем самым преобразуются начальные условия
y(x0
)=y0
, z(x0
)=z0
, z0
=y/
0
(17)
1.5 Практическая часть
Здесь решается уравнение dy/dx = 2x-y+x2
на интервале [0,2], начальное значение y(0)=0, для оценки точности задано также точное решение в виде функции u(x)=x2
. Оценка погрешности делается в нормеL1
, как и принято в данном случае

Рисунок 2
Mathcad имеет ряд встроенных функций, предназначенных для решения обыкновенных дифференциальных уравнений (ОДУ). При решении ОДУ искомой величиной является функция. При использовании любых методов численного интегрирования необходимо, чтобы были заданы по крайней мере следующие величины:
начальные условия;
набор точек в которых нужно найти решение;
само дифференциальное уравнение, записанное в некотором специальном виде, который будет описан ниже.
Один из наиболее эффективных алгоритмов интегрирования ОДУ основан на численном методе Рунге-Кутты четвертого порядка. Функция, реализующая этот метод, имеет вид rkfixed (y,x1
,x2
, npoints,D)
Здесь:
y-вектор начальных условий размерности n, где n- порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений);
x1
, x2
– граничные точки интервала, на котором ищется решение дифференциального уравнения. Начальные условия ,заданные в векторе y,- это значение решения в точке x1
;
npoints- число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1+npoints) в матрице, возвращаемой функцией rkfixed;
D(x,y) – функция,возвращающая значение в виде вектора n элементов, содержащих первые производные неизвестных функций.
2.1 Метод Эйлера
Если задачу об отыскании всех решений дифференциального уравнения удается свести к конечному числу алгебраических операций, операций интегрирования и дифференцирования известных функций, то говорят, что уравнениеинтегрируется в квадратурах. В приложениях крайне редко встречаются уравнения, интегрируемые в квадратурах. Поэтому для исследования дифференциальных уравнений широко используются приближенные, численные методы их решения.
Численное решение
на отрезке [a, b] задачи Коши
y' =f(x, y), y(a) =y0
состоит в построении таблицы приближенных значений
y0
,y1
, ...,yi
, ...yN
решенияy(x)в узлах сетки
a=x0
<x1
< ... <xi
< ...<xN
=b, y(xi
)@yi
.
Еслиxi
=a+ i h, h=(b-a)/ N,то сетка  называетсяравномерной. называетсяравномерной.
Численный метод решения задачи Коши называетсяодношаговым
, если для вычисления решения в точкеx0
+hиспользуется информация о решении только в точкеx0
.
Простейший одношаговый метод численного решения задачи Коши -метод Эйлера
. В методе Эйлера величиныyi
вычисляются по формуле
yi
+1 =yi
+hf(xi
,yi
), i= 0, 1
Найдем методом Эйлера на [0, 1] с шагом h=0.2 приближенное решение задачи Коши
Для того чтобы изменить стиль изображения, щелкните дважды по полю графиков и установите соответствующие параметры
Определим правую часть уравнения
Расчетные формулы метода Эйлера для решения этой задачи имеют вид
x0=0, y0= 1, xi+1 = xi + 0.2, yi+1 = yi + 0.2(sinxi - cosyi), i =0, 1, ..., 4.
Изобразим приближенное решение графически.
y' = sin x – cos y, y(0)=1.
Определим диапазон изменения номера точки i=0,1, ..., 4
Знак присваивания можно ввести щелчком по соответствующей позиции в панели Evaluation.

Определим начальное условие - решение в начальной точке
Для того чтобы ввести символ диапазона изменения индекса <..>, щелкните по соответствующей позиции в панели Matrix или введите с клавиатуры символ <;> ("точка с запятой")

Определим шаг формулы Эйлера - шаг интегрирования
Для того чтобы ввести нижний индекс переменной, щелкните по соответствующей позиции в панели Matrix или в панели Calculator


Определим по формулам Эйлера значения приближенного решения в узлах сетки

Выведем в рабочий документ вычисленные значения решения


Построим график найденного решения y(x)


Для того чтобы вывести значение переменной в рабочий документ, введите имя переменной, знак равенства и щелкните по рабочему документу вне выделяющей рамки
Для того чтобы построить график приближенного решения, щелкните в панели Graph по пиктограмме декартова графика, введите в помеченной позиции возле оси абсцисс обозначение компонент вектора, содержащего значения узлов сетки, а в позиции возле оси ординат - обозначение компонент вектора, содержащего значения приближенного решения в узлах сетки; затем щелкните по свободному месту в рабочем документе вне поля графиков.



2.2 Метод Эйлера с шагом h/2
.
Метод Эйлера допускает простуюгеометрическую интерпретацию. Пусть известна точка (xi
,yi
) интегральной кривой уравненияy'=f(x, y).
Касательная к интегральной кривой уравнения, проходящая через эту точку, определяется уравнением
y=yi
+f(xi
,yi
)(x-xi
).
Следовательно, вычисленная методом Эйлера точка (xi+
1 ,yi+
1 ),
Гдеxi+
1=xi
+h,yi+
1=yi
+h f(xi
,yi
), лежит на этой касательной.
Найдем методом Эйлера на [0, 1] с шагом h=0.2 и с шагом h=0.1 приближенное решение задачи Коши
y' = sin x – cosy,y(0)=1.
Изобразим приближенные решения графически.
Расчетные формулы метода Эйлера для решения этой задачи имеют вид
x0=0, y0= 1, xi+1 = xi + 0.2, yi+1 = yi + 0.2(sinxi - cosyi), i =0, 1, ..., 4
xi+1 = xi + 0.2, yi+1 = yi + 0.2(sinxi - cosyi), i =0, 1, ..., 9
Определим правую часть уравнения

Знак присваивания можно ввести щелчком по соответствующей позиции в панели Evaluation.
Определим диапазон изменения номера точки i=0,1, ..., 4 для вычислений с шагом h=0.2

Для того чтобы ввести символ диапазона изменения индекса <..>, щелкните по соответствующей позиции в панели Matrix или введите с клавиатуры символ <;> ("точка с запятой")
При решении задачи с шагом h=0.2 назовем шаг h1, аргумент - x1, а решение - y1.
Определим начальное условие


Для того чтобы ввести нижний индекс переменной, щелкните по соответствующей позиции в панели Matrix или в панели Calculator
Определим шаг формулы Эйлера - шаг интегрирования

Определим по формулам Эйлера значения приближенного решения в узлах сетки


Выведем в рабочий документ вычисленные значения решения
Для того чтобы вывести значение переменной в рабочий документ, введите имя переменной, знак равенства и щелкните по рабочему документу вне выделяющей рамки


Построим график найденного решения y1(x1)


Для того чтобы построить график приближенного решения, щелкните в панели Graph по пиктограмме декартова графика, введите в помеченной позиции возле оси абсцисс обозначение компонент вектора, содержащего значения узлов сетки, а в позиции возле оси ординат - обозначение компонент вектора, содержащего значения приближенного решения в узлах сетки; затем щелкните по свободному месту в рабочем документе вне поля графиков.
Определим диапазон изменения номера точки i=0,1, ..., 9 для вычислений с шагом h=0.1

Для того чтобы ввести символ диапазона изменения индекса <..>, щелкните по соответствующей позиции в панели Matrix или введите с клавиатуры символ <;> ("точка с запятой")
При решении задачи с шагом h=0.1 назовем шаг h2, аргумент - x2, а решение - y2.
Определим начальное условие


Для того чтобы ввести нижний индекс переменной, щелкните по соответствующей позиции в панели Matrix или в панели Calculator
Определим шаг формулы Эйлера - шаг интегрирования

Определим по формулам Эйлера значения приближенного решения в узлах сетки


Выведем в рабочий документ вычисленные значения решения. Для сравнения рядом выведены значения решения, вычисленные с большим шагом




Построим график решения y2(x2)


Построим на одном графике оба приближенные решения


Для того чтобы одновременно построить графики нескольких функций от разных аргументов, щелкните в панели Graph по пиктограмме декартова графика, введите в помеченной позиции у оси абсцисс имя первого аргумента, запятую, имя второго аргумента, и т.д., разделяя имена аргументов запятой.
Аналогично, в позиции возле оси ординат введите имя функции первого аргумента, запятую, имя функции второго аргумента и т.д.разделяя имена функций запятой.
Когда функции определены, щелкните по рабочему документу вне поля графиков.

2.3 Метод Рунге – Кутты
Методом Рунге-Кутты четвертого порядкаточности называют одношаговый метод, относящийся к широкому классу методов Рунге-Кутты. В этом методе величиныyi+
1 вычисляются по следующим формулам:
yi
+1 =yi
+h(k1
+ 2k2
+ 2k3
+k4
)/6 , i= 0, 1, ...
k1
=f(xi
,yi
),
k2
=f(xi
+h/2,yi
+hk1
/2),
k3
=f(xi
+h/2,yi
+hk2
/2),
k4
=f(xi
+h,yi
+hk3
).
Найдем на [0, 1]приближенноерешение задачи Кошиy' = sinx– cosy,y(0)=1методом Рунге-Кутты 4-го порядка с шагом h=0.2 и методом Эйлера с тем же шагом.Изобразим оба приближенные решения графически
Для решения задачиметодом Рунге-Кутты воспользуемся функциейrkfixed
Определим начальное условие - решение в начальной точке

Для того чтобы ввести нижний индекс переменной, щелкните по соответствующей позиции в панели Matrix или в панели Calculator
Определим правую часть уравнения

Знак присваивания можно ввести щелчком по соответствующей позиции в панели Evaluation.
Вычислим приближенное решение на отрезке [0,1], выполнив n=1/h=5 одинаковых шагов, методом Рунге-Кутты 4-го порядка; обозначим приближенное решение Y

Выведем в рабочий документ вычисленное приближенное решение
Для того чтобы вывести значение переменной в рабочий документ, введите имя переменной, знак равенства и щелкните по рабочему документу вне выделяюшей рамки

В первом столбце приведены значения x, во втором столбце - соответствующие значения приближенного решения
Решим ту же задачу методом Эйлера







Выведем в рабочий документ вычисленное приближенное решение, и, для сравнения, решение, вычисленное методом Рунге-Кутты



Построим графики приближенных решений

Для того чтобы построить график приближенного решения, щелкните в панели Graph по пиктограмме декартова графика, введите в помеченной позиции возле оси абсцисс имя первого столбца матрицы Y, содержащего значения x в узлах сетки, а в позиции возле оси ординат - имя второго столбца, содержащего значения приближенного решения в узлах сетки; затем щелкните по свободному месту в рабочем документе вне поля графиков.
Для того чтобы одновременно построитьграфики нескольких функций от разных аргументов, щелкните в панели Graph по пиктограмме декартова графика, введите в помеченной позиции у оси абсцисс имя первого аргумента, запятую, имя второго аргумента, и т.д., разделяя имена аргументов запятой.
Аналогично, в позиции возле оси ординат введите имя функции первого аргумента, запятую, имя функции второго аргумента и т.д. разделяя имена функций запятой.
Когда функции определены, щелкните по рабочему документу вне поля графиков.

Для того чтобы ввести номер столбца, щелкните по соответствующему символу в панели Matrix

Для того чтобы изменить стиль изображения, щелкните дважды по полю графиков и установите в окне соответствующие параметры
Заключение
Миллионы людей занимаются математическими расчетами, иногда в силу влечения к таинствам математики и ее внутренней красоте, а чаще в силу профессиональной или иной необходимости, не говоря уже об учебе. Ни одна серьезная разработка в любой отрасли науки и производства не обходится без трудоемких математических расчетов. Система Mathcadпользуется огромной популярностью во всем мире, позволяя готовить вполне профессиональные документы, имеющие вид статей и книг по математике.
Программа MicrosoftExcel входит в офисный пакет MicrosoftOfficeи предназначена для подготовки и обработки электронных таблиц под управлением операционной системой Windows. MicrosoftExcel – это многофункциональный, мощный редактор электронных таблиц. Он представляет возможность производить различные расчеты, составлять списки, сметы и что немаловажно, строить наглядные графики и диаграммы.
MathCAD – это мощная и в то же время простая универсальная среда для решения задач в различных отраслях науки и техники, финансов и экономики, физики и астрономии, строительства и архитектуры, математики и статистики, организации производства и управления… Она располагает широким набором инструментальных, информационных и графических средств. Сегодня MathCAD – одна из самых популярных математических систем. Она пользуется большим спросом у студентов, инженеров, экономистов, менеджеров, научных работников и всех тех, чья деятельность связана с количественными методами расчета.
Microsoft Excel ‑ средство для работы с электронными таблицами, намного превышающее по своим возможностям существующие редакторы таблиц, первая версия данного продукта была разработана фирмой Microsoft в 1985 году. Microsoft Excel ‑ это простое и удобное средство, позволяющее проанализировать данные и, при необходимости, проинформировать о результате заинтересованную аудиторию, используя Internet. Microsoft®
Excel разработан фирмой Microsoft, и является на сегодняшний день самым популярным табличным редактором в мире. Кроме стандартных возможностей его отличает следующие возможности, он выводит на поверхность центральные функции электронных таблиц и делает их более доступными для всех пользователей. Для облегчения работы пользователя упрощены основные функции, создание формул, форматирование, печать и построение графиков.
Данная курсовая работа позволила мне более близко познакомится с пакетом прикладных программ MathCAD и MicrosoftExcel. Мной было рассмотрено несколько способов решения дифференциальных уравнений.
Всё это позволило в полном объеме усвоить лекционный материал и понять перспективы использования вычислительной техники при решении различных задач практического характера.
Список литературы
1. Индейкин В. В. Табличный редактор Microsoft Excel. Учебное пособие. – Казань, 1999. – 75с.
2. Кудрявцев Е. М. MathCAD 2000 Pro. – М.: ДМК Пресс, 2001. – 571с.
3. Руководство пользователя Mathcad 6.0 и Mathcad PLUS 6.0. – Компания SoftLine. http://www.exponenta.ru/soft/Mathcad/UsersGuide/0.asp
|