Контрольная работа: Изучение измерительных приборов. Оценка погрешностей измерений физических величин
|
Название: Изучение измерительных приборов. Оценка погрешностей измерений физических величин Раздел: Рефераты по физике Тип: контрольная работа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Министерство образования РФ Рязанская государственная радиотехническая академия Кафедра ОиЭФ Контрольная работа Изучение измерительных приборов. Оценка погрешностей измерений физических величин Рязань 2004 Цель работы Изучить порядок оценки погрешностей при прямых и косвенных измерениях физических величин, ознакомиться с устройством, принципом действия простейших измерительных приборов и определить объём заданного тела. Приборы и принадлежности: штангенциркуль, микрометр, исследуемое тело. Элементы теории Измерение физической величины – процесс сравнения измеряемой величины с помощью технических средств с однородной ей величиной, условно принятой за единицу. Различают два вида измерений: прямые и косвенные. Прямое измерение – это измерение, при котором искомое значение величины находят непосредственно из опыта. Косвенное измерение – это измерение, при котором искомое значение величины находят на основании известной функциональной зависимости между ней и величинами полученными при проведении прямых измерений. Погрешностью измерения является величина отклонения результата измерений от истинного значения измеряемой величины. Действительным значением физической величины называется её значение, найденное экспериментальным путём и максимально приближенное к истинному значению. Как таковое действительным значением может являться среднее арифметическое отдельных измерений.
при Абсолютная погрешность – это модуль отклонения результата
Относительная погрешность – это погрешность, выраженная отношением абсолютной погрешности к действительному значению измеряемой величины.
Представленная погрешность может содержать в себе систематическую составляющую и случайную составляющую. Систематической погрешностью называют погрешность, сохраняющую постоянное значение и знак или меняющуюся по известному закону при повторных измерениях одной и одной и той же величины в одинаковых условиях. Случайной погрешностью является погрешность, возникающая при повторных изменениях одной и той же величины в виду изменения внешних условий. «Выпады» («промахи») – значительные отклонения полученных результатов от ожидаемых, при известных погрешностях. Средняя арифметическая погрешность измерения физической величины.
при Среднеквадратичное отклонение результата измерения величины
Расчётная часть Оценка погрешности при прямых вычислениях величин h и d, произведенные штангенциркулем.
Найдём действительное значение измеряемой величины <h>. <h> <h> Найдём абсолютную погрешность (Dhi) для каждого i –ого значения измеренной величины. Dhi = hi - <h>; Dh1 = 14,9 – 14,87 = 0,03 (мм) Dh4 = 14,9 – 14,87 = 0,03 (мм) Dh2 = 14,85 – 14,87 = -0,02 (мм) Dh5 = 14,85 – 14,87 = -0,02 (мм) Dh3 = 14,85 – 14,87 = -0,02 (мм) Вычислим систематическую погрешность (Dс). Dс = Найдём систематическую составляющую среднеквадратичной погрешности (
Вычислим случайную составляющую среднеквадратичной погрешности (
Подсчитаем суммарную среднеквадратичную погрешность
Вычислим случайную погрешность (Dсл). Dсл = tc Dсл = 2,78 Оценим полную погрешность (Dh) Dh = Dh = Найдём относительную погрешность
Найдём действительное значение измеряемой величины <d> <d> < в > Ddi = di - <d>; Dd1 = 13,9 – 13,58 = 0,32 (мм) Dd2 = 13,9 – 13,58 = 0,32 (мм) Dd3 = 13,3 – 13,58 = -0,28 (мм) Dd4 = 13,4 – 13,58 = 0,18 (мм) Dd5 = 13,4 – 13,58 = 0,18 (мм) (
Dсл = tс Dсл = 2,78´0,132= 0,36 (мм) Dd = Dd =
Рассчитаем погрешность при косвенных вычислениях величины V, на основе величин h и d, измеренных штангенциркулем. Расчёт среднего значения величины V <V>=f(<h>, <d>); <V> <V>
Расчёт абсолютной погрешности величины V DV Вычислим относительную погрешность величины V
V=<V> V=2152,68
P = 0,95 Оценка погрешности при прямых вычислениях величин h и d, произведенные микрометром.
Найдём действительное значение измеряемой величины <h> <h> < h > Dhi = hi - <h>; Dh1 = 15,04 – 15,11= -0,07 (мм) Dh2 = 15,4 – 15,11 = 0,29 (мм) Dh3 = 15,03 – 15,11 = -0,08 (мм) Dh4 = 15,04 – 15,11 = -0,07 (мм) Dh5 = 15,04 – 15,11 = -0,07 (мм) Dс = Dс = 1,1
Dсл = tс Dсл = 2,78 Dh = Dh =
<d> < в > Ddi = di - <d>; Dd1 = 14,04 – 14,05 = -0,01 (мм) Dd4 = 14,05 – 14,05 = 0 (мм) Dd2 = 14,05 – 14,05 = 0 (мм) Dd5 = 14,06 – 14,05 = 0,01 (мм) Dd3 = 14,05 – 14,05 = 0 (мм)
Dсл = tс Dсл = 2,78´3,3´10-3= 9,17´10-3 (мм) Dd = Dd =
Рассчитаем погрешность при косвенных вычислениях величины V, на основе величин h и d, измеренных микрометром. <V>=f(<h>, <d>); <V> <V>
DV DV
V=<V> V=2341,46
P = 0,95 |
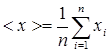
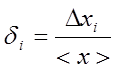

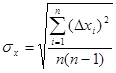
 ;
; ;
;  (мм3)
(мм3)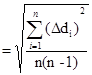 ;
;