Численное решение уравнения Шредингера средствами Java
Содержание
Введение
1. Уравнение Шредингера и физический смысл его решений
1.1 Волновое уравнение Шредингера
1.2 Волновые функции в импульсном представлении
2. Методы численного решения нестационарного уравнения Шредингера
2.1 Метод конечных разностей для одномерного нестационарного уравнения Шредингера
2.2 Преобразование Фурье
2.3 Метод аппроксимации оператора эволюции (split-operatormethod)
3. Методы численного решения стационарного уравнения Шредингера
3.1 Метод Нумерова
4. Программная реализация численных методов средствами Java
4.1 Обзор языка программирования Java
4.2 Элементы программирования Java 2 используемые в работе
Заключение
Список использованных источников
Введение
Известно, что курс квантовой механики является одним из сложных для восприятия. Это связано не столько с новым и "необычным" математическим аппаратом, сколько прежде всего с трудностью осознания революционных, с позиции классической физики, идей, лежащих в основе квантовой механики и сложностью интерпретации результатов.
В большинстве учебных пособий по квантовой механике изложение материала основано, как правило, на анализе решений стационарного уравнений Шредингера. Однако стационарный подход не позволяет непосредственно сопоставить результаты решения квантовомеханической задачи с аналогичными классическими результатами. К тому же многие процессы, изучаемые в курсе квантовой механики (как, например, прохождение частицы через потенциальный барьер, распад квазистационарного состояния и др.) носят в принципе нестационарный характер и, следовательно, могут быть поняты в полном объеме лишь на основе решений нестационарного уравнения Шредингера. Поскольку число аналитически решаемых задач невелико, использование компьютера в процессе изучения квантовой механики является особенно актуальным.
1. Уравнение Шредингера и физический смысл его решений
1.1 Волновое уравнение Шредингера
Одним из основных уравнений квантовой механики является уравнение Шредингера, определяющее изменение состояний квантовых систем с течением времени. Оно записывается в виде
 (1.1) (1.1)
где Н — оператор Гамильтона системы, совпадающий с оператором энергии, если он не зависит от времени. Вид оператора 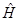 определяется свойствами системы. Для нерелятивистского движения частицы массы определяется свойствами системы. Для нерелятивистского движения частицы массы 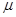 в потенциальном поле U(r) оператор в потенциальном поле U(r) оператор 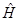 действителен и представляется суммой операторов кинетической и потенциальной энергии частицы действителен и представляется суммой операторов кинетической и потенциальной энергии частицы
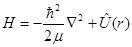 (1.2) (1.2)
Если частица движется в электромагнитном поле, то оператор Гамильтона будет комплексным.
Хотя уравнение (1.1) является уравнением первого порядка по времени, вследствие наличия мнимой единицы оно имеет и периодические решения. Поэтому уравнение Шредингера (1.1) часто называют волновым уравнением Шредингера, а его решение называют волновой функцией, зависящей от времени. Уравнение (1.1) при известном виде оператора Н позволяет определить значение волновой функции 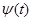 в любой последующий момент времени, если известно это значение в начальный момент времени. Таким образом, волновое уравнение Шредингера выражает принцип причинности в квантовой механике. в любой последующий момент времени, если известно это значение в начальный момент времени. Таким образом, волновое уравнение Шредингера выражает принцип причинности в квантовой механике.
Волновое уравнение Шредингера может быть получено на основании следующих формальных соображений. В классической механике известно, что если энергия задана как функция координат и импульсов
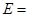 H H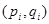 ,(1.3) ,(1.3)
то переход к классическому уравнению Гамильтона—Якоби для функции действия S
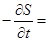 H H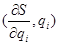
можно получить из (1.3) формальным преобразованием
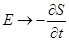 , , 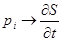
Таким же образом уравнение (1.1) получается из (1.3) при переходе от (1.3) к операторному уравнению путем формального преобразования
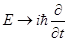 , , 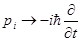 (1.4) (1.4)
если (1.3) не содержит произведений координат и импульсов, либо содержит такие их произведения, которые после перехода к операторам (1.4) коммутируют между собой. Приравнивая после этого преобразования результаты действия на функцию 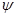 операторов правой и левой частей полученного операторного равенства, приходим к волновому уравнению (1.1). Не следует, однако, принимать эти формальные преобразования как вывод уравнения Шредингера. Уравнение Шредингера является обобщением опытных данных. Оно не выводится в квантовой механике, так же как не выводятся уравнения Максвелла в электродинамике, принцип наименьшего действия (или уравнения Ньютона) в классической механике. операторов правой и левой частей полученного операторного равенства, приходим к волновому уравнению (1.1). Не следует, однако, принимать эти формальные преобразования как вывод уравнения Шредингера. Уравнение Шредингера является обобщением опытных данных. Оно не выводится в квантовой механике, так же как не выводятся уравнения Максвелла в электродинамике, принцип наименьшего действия (или уравнения Ньютона) в классической механике.
Легко убедиться, что уравнение (1.1) удовлетворяется при 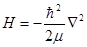 волновой функцией волновой функцией
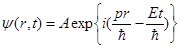 , ,
описывающей свободное движение частицы с определенным значением импульса. В общем случае справедливость уравнения (1.1) доказывается согласием с опытом всех выводов, полученных с помощью этого уравнения.
Покажем, что из уравнения (1.1) следует важное равенство
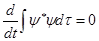 ,(1.5) ,(1.5)
указывающее на сохранение нормировки волновой функции с течением времени. Умножим слева (1.1) на функцию 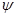 *, a уравнение, комплексно сопряженное к (1.1), на функцию *, a уравнение, комплексно сопряженное к (1.1), на функцию 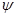 и вычтем из первого полученного уравнения второе; тогда находим и вычтем из первого полученного уравнения второе; тогда находим
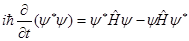 ,(1.6) ,(1.6)
Интегрируя это соотношение по всем значениям переменных и учитывая самосопряженность оператора 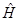 , получаем (1.5). , получаем (1.5).
Если в соотношение (1.6) подставить явное выражение оператора Гамильтона (1.2) для движения частицы в потенциальном поле, то приходим к дифференциальному уравнению (уравнение непрерывности)
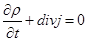 , (1.7) , (1.7)
где 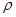 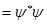 является плотностью вероятности, а вектор является плотностью вероятности, а вектор
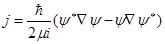 (1.8) (1.8)
можно назвать вектором плотности тока вероятности.
Комплексную волновую функцию 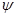 всегда можно представить в виде всегда можно представить в виде
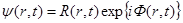
где 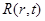 и и 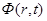 — действительные функции времени и координат. Таким образом, плотность вероятности — действительные функции времени и координат. Таким образом, плотность вероятности
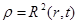 , ,
а плотность тока вероятности
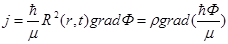 .(1.9) .(1.9)
Из (1.9) следует, что j = 0 для всех функций 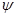 , у которых функция Ф не зависит от координат. В частности, j= 0 для всех действительных функций , у которых функция Ф не зависит от координат. В частности, j= 0 для всех действительных функций 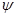 . .
Решения уравнения Шредингера (1.1) в общем случае изображаются комплексными функциями. Использование комплексных функций весьма удобно, хотя и не необходимо. Вместо одной комплексной функции 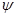 состояние системы можно описать двумя вещественными функциями состояние системы можно описать двумя вещественными функциями 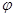 и и 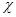 , удовлетворяющими двум связанным уравнениям. Например, если оператор Н — вещественный, то, подставив в (1.1) функцию , удовлетворяющими двум связанным уравнениям. Например, если оператор Н — вещественный, то, подставив в (1.1) функцию 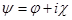 и отделив вещественную и мнимую части, получим систему двух уравнений и отделив вещественную и мнимую части, получим систему двух уравнений
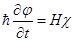 , , 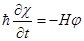 , ,
при этом плотность вероятности и плотность тока вероятности примут вид
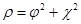 , , 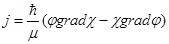 . [1] . [1]
1.2 Волновые функции в импульсном представлении.
Фурье-образ 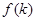 волновой функции волновой функции 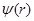 характеризует распределение импульсов в квантовом состоянии характеризует распределение импульсов в квантовом состоянии 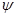 . Требуется вывести интегральное уравнение для . Требуется вывести интегральное уравнение для 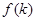 с Фурье-образом потенциала в качестве ядра. с Фурье-образом потенциала в качестве ядра.
Решение. Между функциями 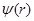 и и 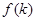 имеются два взаимно обратных соотношения. имеются два взаимно обратных соотношения.
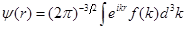 (2.1) (2.1)
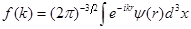 (2.2) (2.2)
Если соотношение (2.1) использовать в качестве определения 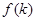 и применить к нему операцию и применить к нему операцию 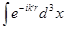 , то с учетом определения 3-мерной , то с учетом определения 3-мерной 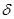 -функции, -функции,
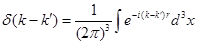 , ,
в результате, как нетрудно убедиться, получится обратное соотношение (2.2). Аналогичные соображения использованы ниже при выводе соотношения (2.8).
Положим далее
 ,(2.3) ,(2.3)
тогда для Фурье-образа потенциала будем иметь
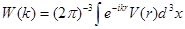 (2.4) (2.4)
Предполагая, что волновая функция 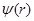 удовлетворяет уравнению Шредингера удовлетворяет уравнению Шредингера
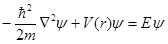 (2.5) (2.5)
Подставляя сюда вместо 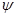 и и 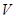 соответственно выражения (2.1) и (2.3), получаем соответственно выражения (2.1) и (2.3), получаем

В двойном интеграле перейдем от интегрирования по переменной 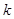 к интегрированию по переменной к интегрированию по переменной 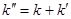 , а затем эту новую переменную вновь обозначим посредством , а затем эту новую переменную вновь обозначим посредством 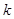 . Интеграл по . Интеграл по 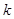 обращается в нуль при любом значении обращается в нуль при любом значении 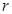 лишь в том случае, когда само подынтегральное выражение равно нулю, но тогда лишь в том случае, когда само подынтегральное выражение равно нулю, но тогда
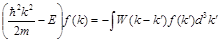 .(2.6) .(2.6)
Это и есть искомое интегральное уравнение с Фурье-образом потенциала 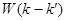 в качестве ядра. Конечно, интегральное уравнение (2.6) можно получить только при условии, что Фурье-образ потенциала (2.4) существует; для этого, например, потенциал в качестве ядра. Конечно, интегральное уравнение (2.6) можно получить только при условии, что Фурье-образ потенциала (2.4) существует; для этого, например, потенциал 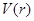 должен убывать на больших расстояниях по меньшей мере как должен убывать на больших расстояниях по меньшей мере как 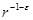 , где , где 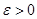 . .
Необходимо отметить, что из условия нормировки
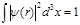 (2.7) (2.7)
следует равенство
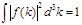 .(2.8) .(2.8)
Это можно показать, подставив в (2.7) выражение (2.1) для функции  : :
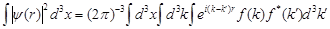 . .
Если здесь сначала выполнить интегрирование по  , то мы без труда получим соотношение (2.8).[2] , то мы без труда получим соотношение (2.8).[2]
2. Методы численного решения нестационарного уравнения Шредингера
2.1 Метод конечных разностей для одномерного нестационарного уравнения Шредингера
В большинстве учебных пособий по квантовой механике изложение материала основано, как правило, на анализе решений стационарного уравнений Шредингера. Однако стационарный подход не позволяет непосредственно сопоставить результаты решения квантовомеханической задачи с аналогичными классическими результатами. К тому же многие процессы, изучаемые в курсе квантовой механики (как, например, прохождение частицы через потенциальный барьер, распад квазистационарного состояния и др.) носят в принципе нестационарный характер и, следовательно, могут быть поняты в полном объеме лишь на основе решений нестационарного уравнения Шредингера. Поскольку число аналитически решаемых задач невелико, использование компьютера в процессе изучения квантовой механики является особенно актуальным.
Нестационарное уравнение Шредингера, определяющее эволюцию волновой функции во времени, представляет собой дифференциальное уравнение первого порядка по времени и имеет следующий вид
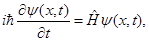 (3.1) (3.1)
где 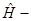 оператор полной энергии системы. Для одномерного случая оператор полной энергии системы. Для одномерного случая
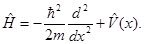
Общее решение уравнения (1) формально можно записать в виде
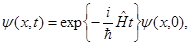 (3.2) (3.2)
где 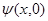 - волновая функция системы в момент времени - волновая функция системы в момент времени 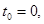
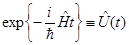 - оператор эволюции (пропагатор). - оператор эволюции (пропагатор).
Особенностью выражения (3.2) является то, что в показателе экспоненты стоит оператор. Определить действие оператора эволюции на волновую функцию можно, например, разложив ее по собственным функциям оператора 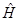 . Так, в случае дискретного спектра . Так, в случае дискретного спектра 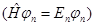 выражение для волновой функции в произвольный момент времени имеет вид выражение для волновой функции в произвольный момент времени имеет вид
 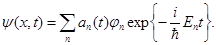 (3.3) (3.3)
Аналогичное выражение может быть получено и для непрерывного спектра.
Разложение (3.3) удобно использовать в тех случаях, когда решения стационарного уравнения Шредингера для конкретной задачи являются известными. Но к сожалению круг таких задач очень ограничен. Большинство современных численных методов решения уравнения (3.1) основаны на использовании различных аппроксимаций оператора эволюции  . Так, например, разложение оператора эволюции в ряд Тейлора с сохранением первых двух членов дает следующую схему . Так, например, разложение оператора эволюции в ряд Тейлора с сохранением первых двух членов дает следующую схему
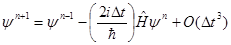 ,(3.4) ,(3.4)
здесь 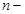 номер шага по времени. Существенным недостатком этого алгоритма является необходимость знать волновую функцию в моменты номер шага по времени. Существенным недостатком этого алгоритма является необходимость знать волновую функцию в моменты 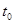 и и 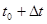 . Кроме того, для оценки действия оператора . Кроме того, для оценки действия оператора 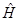 на функцию на функцию 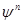 нужно вычислять вторую производную по координате. Простейшая конечно-разностная аппроксимация второй производной нужно вычислять вторую производную по координате. Простейшая конечно-разностная аппроксимация второй производной
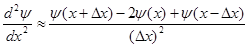 (3.5) (3.5)
дает неудовлетворительный результат. (См. программный блок 1)[3]
2.2 Преобразование Фурье
Начнем с комплексного ряда Фурье
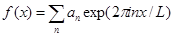
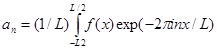
Рассмотрим случай L .Тогда сумму можно преобразовать в интеграл следующим образом: определим .Тогда сумму можно преобразовать в интеграл следующим образом: определим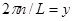 и и 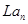 =g(y).Так как =g(y).Так как  возрастает каждый раз на единицу ,то возрастает каждый раз на единицу ,то
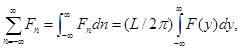  где где 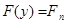 . .
Таким образом, полученные выше формулы приобретают вид
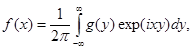 
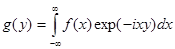  (4.1) (4.1)
Величина 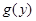 называется преобразованием Фурье от называется преобразованием Фурье от 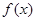 и наоборот. Положение множителя и наоборот. Положение множителя 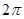 довольно произвольно; часто величины довольно произвольно; часто величины 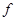 и и 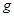 определяют более симметрично: определяют более симметрично:
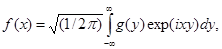 
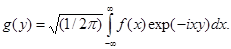  (4.2) (4.2)
Выражения (4.1) или (4.2) можно скомбинировать следующим образом:
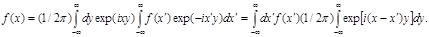 (4.3) (4.3)
Равенство (4.3) удовлетворяется для любой функции 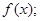 это позволяет сделать интересный вывод об интеграле это позволяет сделать интересный вывод об интеграле 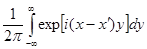 как функции как функции 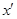 . Он равен нулю всюду, кроме точки . Он равен нулю всюду, кроме точки 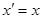 , а интеграл от него по любому промежутку ,включающему , а интеграл от него по любому промежутку ,включающему 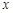 , равен единице, т.е. эта функция имеет бесконечно высокий и бесконечно узкий пик в точке , равен единице, т.е. эта функция имеет бесконечно высокий и бесконечно узкий пик в точке 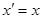 . .
Обычно определяют  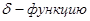 (Дирака) (Дирака) 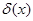 следующим образом: следующим образом:
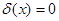 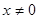
  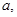 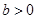 (4.4) (4.4)
Из этих уравнений следует, что
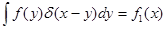 (4.5) (4.5)
для любой функции 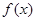 , в случае если интервал интегрирования включает точку , в случае если интервал интегрирования включает точку 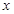 . .
Проделанные выше операции над интегралами Фурье показали, что
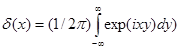 (4.6) (4.6)
Это интегральное представление 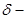 функции. функции.
Дельта – функцию можно использовать, чтобы выразить важный интеграл 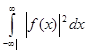 через преобразование Фурье (4.1) от через преобразование Фурье (4.1) от 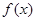 : :
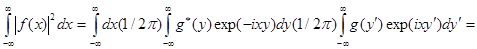
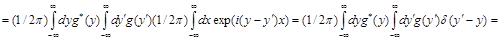
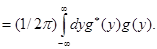 (4.7) (4.7)
Это равенство называется теоремой Парсеваля. Она полезна для понимания физической интерпретации преобразования Фурье для 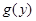 , если известен физический смысл , если известен физический смысл 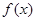 . .
Предположим, что 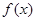 четная функция. Тогда четная функция. Тогда
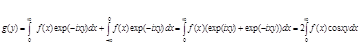
Заметим теперь, что 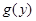 -- также четная функция. Поэтому -- также четная функция. Поэтому
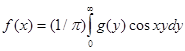 (4.9) (4.9)
Функция 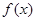 и и 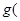  ,определенные теперь только для положительных ,определенные теперь только для положительных 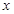 и и 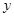 , называются косинус - преобразованиями Фурье по отношению друг к другу. , называются косинус - преобразованиями Фурье по отношению друг к другу.
Рассматривая преобразования Фурье нечетной функции, получаем аналогичные соотношения Фурье между синус - преобразованиями Фурье:
 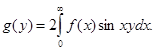 (4.10) (4.10)
Если нужно, можно симметризовать выражения, поставив множитель 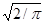 перед каждым интегралом (4.7)-(4.10). [4] перед каждым интегралом (4.7)-(4.10). [4]
2.3 Метод аппроксимации оператора эволюции (split-operator method)
Рассмотрим более подробно другой метод аппроксимации оператора эволюции, в котором отсутствуют недостатки, свойственные рассмотренной выше схеме. Здесь оператор эволюции аппроксимируется симметричным расщеплением оператора кинетической энергии (split-operator method)
 (5.1) (5.1)
Основная погрешность данной аппроксимации связана с некоммутативностью операторов кинетической и потенциальной энергии. Вычисление действия такого оператора на волновую функцию включает следующие шаги. Преобразованная в импульсное представление волновая функция умножается на 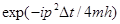 и преобразуется обратно в координатное представление, где умножается на и преобразуется обратно в координатное представление, где умножается на 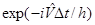 . Полученный результат снова преобразуется в импульсное представление, умножается на . Полученный результат снова преобразуется в импульсное представление, умножается на 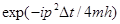 преобразуется обратно в координатное представление. На этом один шаг по времени завершается. Переход от одного представления к преобразуется обратно в координатное представление. На этом один шаг по времени завершается. Переход от одного представления к
другому осуществляется посредством преобразования Фурье.
В данной курсовой работе используется Гауссов волновой пакет вида 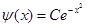 , а также ступенчатый потенциал. Сначала преобразуем нашу волновую функцию из координатного представления в импульсное , а также ступенчатый потенциал. Сначала преобразуем нашу волновую функцию из координатного представления в импульсное
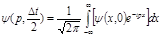 ,(5.2) ,(5.2)
затем умножим полученный результат на 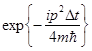 . На этом завершается половина временного шага. Полученный результат снова преобразуется в координатное представление . На этом завершается половина временного шага. Полученный результат снова преобразуется в координатное представление
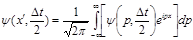 (5.3) (5.3)
и умножается на  . После чего вновь преобразуется в импульсное представление . После чего вновь преобразуется в импульсное представление
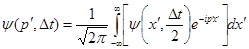 (5.4) (5.4)
и умножается на 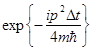 . Завершается шаг по времени еще одним преобразованием полученной волновой функции в координатное представление . Завершается шаг по времени еще одним преобразованием полученной волновой функции в координатное представление
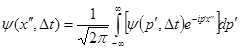 .(5.5) .(5.5)
Один шаг по времени завершен.
В данной работе этот метод реализован в среде Java, ниже приведены программный блок и полученные графики поведения волновой функции в различные моменты времени.
Важная особенность этого метода заключается в том, что действие каждого из операторов оценивается в их соответствующем локальном представлении.
С методической точки зрения ценность нестационарного подхода состоит в существенно большей наглядности и информативности результатов, по сравнению с результатами решения стационарного уравнения Шредингера. Круг задач, которые могут быть рассмотрены на основе решения нестационарного уравнения Шредингера очень разнообразен.
Для иллюстрации вышесказанного рассмотрим задачу о движении частицы в поле потенциального барьера. Хотя стационарный подход позволяет определить коэффициенты прохождения и отражения частицы он, однако, не позволяет рассмотреть реальную пространственно-временную картину движения частицы через потенциальный барьер, которая является существенно нестационарной. Рассмотрение задачи на основе решения нестационарного уравнения Шредингера позволяет не только сопоставить классический и квантовый подход к проблеме, но и получить ответы на ряд вопросов, представляющих значительный практический интерес (например, длительность процесса туннелирования, скорости прошедших и отраженных частиц и т.д.). Ниже мы приводим результаты решения нестационарного уравнения Шредингера для данной задачи. Начальное состояние частицы задано в виде пакета гауссовой формы, движущегося в направлении области действия потенциала. На графиках представлена временная картина туннелирования такого пакета через потенциальный барьер прямоугольной формы в виде "мгновенных снимков" волнового пакета в разные моменты времени. Как видно, при попадании пакета в область действия потенциала его форма нарушается в результате формирования отраженного волнового пакета и его интерференции с падающим на препятствие пакетом. Через некоторое время формируются два пакета: отраженный и прошедший через препятствие. Движение падающего и отраженного пакета можно сопоставить с движение классической частицы, положение которой совпадает с максимумом в распределении вероятности. В случае протяженного потенциала отраженный пакет "отстает" от отраженной от барьера классической частицы. Физически это связано с тем, что пакет частично проникает в классически запрещенную область, в то время как в классике отражение происходит строго в точке скачка потенциала. Образование же прошедшего пакета представляет собой сугубо квантовый эффект не имеющий классических аналогий.[3]
3. Методы численного решения стационарного уравнения Шредингера
3.1 Метод Нумерова
Рассмотрим решения одномерного стационарного уравнения Шредингера (3.1) частицы, движущейся в одномерном потенциале U(x).
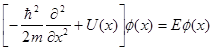 (3.1) (3.1)
Будем при этом полагать, что его форма имеет потенциала, представленного на рис.1: в точках xmin
, xmax
потенциал становится бесконечно большим. Это означает, что в точках xmin
, xmax
расположены вертикальные стенки, а между ними находится яма конечной глубины.
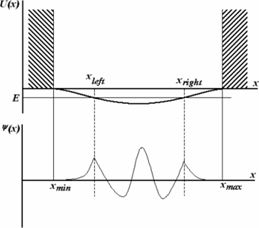
Рисунок 1.
Для удобства дальнейшего решения запишем уравнение Шредингера (3.1) в виде:
 (3.2) (3.2)
Где
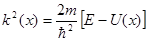 (3.3) (3.3)
С математической точки зрения задача состоит в отыскании собственных функций оператора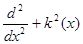 , отвечающим граничным условиям , отвечающим граничным условиям
 (3.4) (3.4)
и соответствующих собственных значений энергии E.
Так как 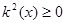 при при 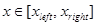 и и 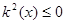 при при 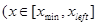 , , 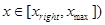 , то можно ожидать, что собственному решению данной задачи соответствует собственная функция, осциллирующая в классически разрешенной области движения , то можно ожидать, что собственному решению данной задачи соответствует собственная функция, осциллирующая в классически разрешенной области движения 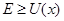 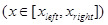 и экспоненциально затухающим в запрещенных областях, где и экспоненциально затухающим в запрещенных областях, где 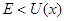 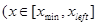 , ,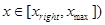 , при , при 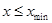 , , 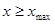 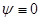 . Так как все состояния частицы в потенциальной яме оказываются связанными (т.е. локализованными в конечной области пространства), спектр энергий является дискретным. Частица, находящаяся в потенциальной яме конечных размеров . Так как все состояния частицы в потенциальной яме оказываются связанными (т.е. локализованными в конечной области пространства), спектр энергий является дискретным. Частица, находящаяся в потенциальной яме конечных размеров 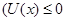 при при 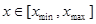 , ,  при при 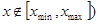 , имеет дискретный спектр при , имеет дискретный спектр при 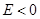 и непрерывный спектр при и непрерывный спектр при  . .
Традиционно для решении задачи о нахождении собственных значений уравнения Шредингера используется метод пристрелки. Идея метода пристрелки состоит в следующем. Допустим, в качестве искомого значения ищется одно из связанных состояний, поэтому в качестве пробного начального значения энергии выбираем отрицательное собственное значение. Проинтегрируем уравнение Шредингера каким-либо известным численным методом на интервале 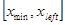 . По ходу интегрирования от . По ходу интегрирования от 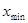 в сторону больших значений в сторону больших значений 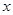 сначала вычисляется решение сначала вычисляется решение 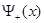 , экспоненциально нарастающее в пределах классически запрещенной области. После перехода через точку поворота , экспоненциально нарастающее в пределах классически запрещенной области. После перехода через точку поворота 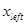 , ограничивающую слева область движения разрешенную классической механикой, решение уравнения становится осциллирующим. Если продолжить интегрирование далее за правую точку поворота , ограничивающую слева область движения разрешенную классической механикой, решение уравнения становится осциллирующим. Если продолжить интегрирование далее за правую точку поворота 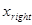 , то решение становится численно неустойчивым. Это обусловлено тем, что даже при точном выборе собственного значения, для которого выполняется условие , то решение становится численно неустойчивым. Это обусловлено тем, что даже при точном выборе собственного значения, для которого выполняется условие 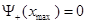 , решение в области , решение в области 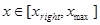 всегда может содержать некоторую примесь экспоненциально растущего решения, не имеющего физического содержания. Отмеченное обстоятельство является общим правилом: интегрирование по направлению вовнутрь области, запрещенной классической механикой, будет неточным. Следовательно, для каждого значения энергии более разумно вычислить еще одно решение всегда может содержать некоторую примесь экспоненциально растущего решения, не имеющего физического содержания. Отмеченное обстоятельство является общим правилом: интегрирование по направлению вовнутрь области, запрещенной классической механикой, будет неточным. Следовательно, для каждого значения энергии более разумно вычислить еще одно решение 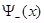 , интегрируя уравнение (3.1) от , интегрируя уравнение (3.1) от  в сторону уменьшения в сторону уменьшения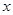 . Критерием совпадения данного значения энергии является совпадение значений функций . Критерием совпадения данного значения энергии является совпадение значений функций 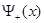 и и 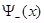 в некоторой промежуточной точке в некоторой промежуточной точке 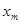 . Обычно в качестве данной точки выбирают левую точку поворота . Обычно в качестве данной точки выбирают левую точку поворота 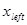 . Так как функции . Так как функции 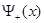 , ,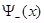 являются решениями однородного уравнения (3.1), их всегда можно нормировать так, чтобы в точке являются решениями однородного уравнения (3.1), их всегда можно нормировать так, чтобы в точке 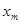 выполнялось условие выполнялось условие 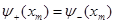 . Помимо совпадения значений функций в точке . Помимо совпадения значений функций в точке 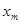 для обеспечения гладкости сшивки решений потребуем совпадения значений их производных для обеспечения гладкости сшивки решений потребуем совпадения значений их производных 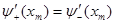
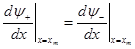 (3.5) (3.5)
Используя в (17) простейшие левую и правую конечно-разностные аппроксимации производных функций 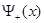 , , 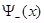 в точке в точке 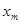 , находим эквивалентное условие гладкости сшивки решений: , находим эквивалентное условие гладкости сшивки решений:
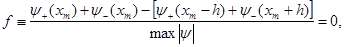 (3.6) (3.6)
Число 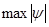 является масштабирующим множителем, который выбирается из условия является масштабирующим множителем, который выбирается из условия 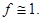 Если точки поворота отсутствуют, т.е. Если точки поворота отсутствуют, т.е. 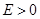 E>0, то в качестве E>0, то в качестве 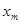 можно выбрать любую точку отрезка можно выбрать любую точку отрезка 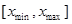 . Для потенциалов, имеющих более двух точек поворота и, соответственно, три или более однородных решений, общее решение получается сшивкой отдельных кусков. В описанном ниже документе, для интегрирования дифференциального уравнения второго порядка мы используем метод Нумерова. Для получения вычислительной схемы аппроксимируем вторую производную трехточечной разностной формулой: . Для потенциалов, имеющих более двух точек поворота и, соответственно, три или более однородных решений, общее решение получается сшивкой отдельных кусков. В описанном ниже документе, для интегрирования дифференциального уравнения второго порядка мы используем метод Нумерова. Для получения вычислительной схемы аппроксимируем вторую производную трехточечной разностной формулой:
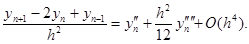 (3.7) (3.7)
Из уравнения (3.1) имеем
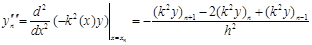 (3.8) (3.8)
Подставив (3.7) в (3.8) и перегруппировав члены, получаем
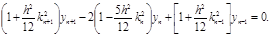 (3.9) (3.9)
Разрешив (3.9) относительно  или или  , найдем рекуррентные формулы для интегрирования уравнения (3.1) вперед или назад по , найдем рекуррентные формулы для интегрирования уравнения (3.1) вперед или назад по 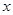 c локальной погрешностью c локальной погрешностью 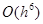 . Отметим, что погрешность данного метода оказывается на порядок выше, чем погрешность метода Рунге-Кутта четвертого порядка. Кроме того данный алгоритм более эффективен, потому что значение функции . Отметим, что погрешность данного метода оказывается на порядок выше, чем погрешность метода Рунге-Кутта четвертого порядка. Кроме того данный алгоритм более эффективен, потому что значение функции 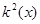 вычисляются только в узлах сетки. Для нахождения численного решения оказывается удобным провести обезразмеривание уравнения (3.1), используя в качестве единиц измерения расстояния вычисляются только в узлах сетки. Для нахождения численного решения оказывается удобным провести обезразмеривание уравнения (3.1), используя в качестве единиц измерения расстояния 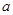 - ширину потенциальной ямы, в качестве единиц измерения энергии - модуль минимального значения потенциала - ширину потенциальной ямы, в качестве единиц измерения энергии - модуль минимального значения потенциала 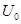 . В выбранных единицах измерения уравнение (3.1) имеет вид . В выбранных единицах измерения уравнение (3.1) имеет вид
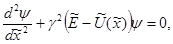 (3.10) (3.10)
где
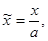 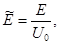 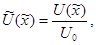 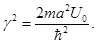 (3.11) (3.11)
Таким образом, вычислительный алгоритм для нахождения собственных функций и собственных значений уравнения Шредингера реализуется следующей последовательностью действий:
1. Задать выражение, описывающее безразмерный потенциал 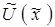 . .
2. Задать значение 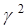 . .
3. Задать пространственную сетку, на которой проводится интегрирование уравнения (3.1).
4. Задать 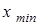 , , 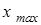 . .
5. Задать начальное значение энергии 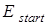 . .
6. Задать конечное значение энергии 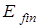 . .
7. Задать шаг изменения энергии 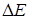 . .
8. Проинтегрировать уравнение (3.1) для значения энергии 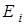 слева направо на отрезке слева направо на отрезке 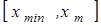 . .
9. Проинтегрировать уравнение (3.1) для значения энергии 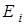 справа налево на отрезке справа налево на отрезке 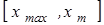 . .
10. Вычислить значения переменной 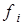 для значения энергии для значения энергии 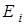 . .
11. Увеличить текущее значение энергии на 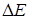 : : 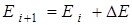 . .
12. Проинтегрировать уравнение (3.1) для значения энергии 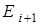 слева направо на отрезке слева направо на отрезке 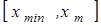 . .
13. Проинтегрировать уравнение (3.1) для значения энергии 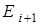 справа налево на отрезке справа налево на отрезке 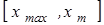 . .
14. Вычислить значения переменной  для значения энергии для значения энергии 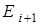 . .
15. Сравнить знаки 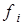 , , 
16. Если 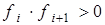 и и 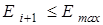 , увеличить текущее значение энергии на , увеличить текущее значение энергии на 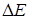 и повторить действия, описанные в пп. 8-17. и повторить действия, описанные в пп. 8-17.
17. Если  , уточнить методом линейной интерполяции. , уточнить методом линейной интерполяции.
18. Если 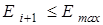 , повторить действия, описанные в пп. 8-18. , повторить действия, описанные в пп. 8-18.
19. Если 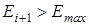 , закончить вычисления.[5] , закончить вычисления.[5]
4. Программная реализация численных методов средствами Java
4.1 Обзор языка программирования Java
Java связан с C++, который является прямым потомком С. Многое в характере Java унаследовано от этих двух языков. От С Java получил его синтаксис. На многие из объектно-ориентированных свойств Java повлиял C++. Некоторые из определяющих характеристик Java происходят от его предшественников. Кроме того, создание Java глубоко внедрилось в процессы усовершенствования и адаптации, которые проявились в языках машинного программирования в течение последних трех десятилетий. Каждое новшество в проекте языка управлялось потребностью решить фундаментальную проблему, с которой не справились предшествующие языки. Java не является исключением.
Internet помог катапультировать Java на передний край программирования, aJava, в свою очередь, имел глубокое влияние на Internet. Этому есть простое объяснение: Java разворачивает вселенную объектов, которые могут свободно перемещаться в киберпространстве. В сети две очень широких категории объектов передаются между сервером и вашим персональным компьютером — пассивная информация и динамические, активные программы. Например, когда вы читаете вашу электронную почту, то рассматриваете пассивные данные. Даже, когда вы загружаете программу, ее код — это все еще только пассивные данные до тех пор, пока вы их не начнете выполнять. Однако на ваш компьютер может быть передан объект второго типа — динамическая, самовыполняющаяся программа. Такая программа — активный агент на компьютере клиента, все же инициализируется сервером. Например, сервер мог бы предоставить (клиенту) программу, чтобы должным образом отображать данные, посылаемые клиенту.
С
толь же желательными, как и динамические, являются сетевые программы. Они также порождают серьезные проблемы в области защиты и мобильности. До. Java, киберпространство было эффективно закрыто для половины объектов, которые теперь живут там. Кроме того, Java имеет дело с захватывающе новой формой программ — апплетами.
Java можно использовать, чтобы создать два типа программ — приложения и апплеты. Приложение — это программа, которая выполняется на вашем компьютере с помощью его операционной системы. То есть, приложение, с
озданное с помощью Java, более или менее подобно приложению, созданному с использованием С или C++. При создании приложения Java не намного отличается от любого другого машинного языка. Более важной является способность Java создавать апплеты. Апплет — это приложение, разработанное для передачи по Internet и выполняемое совместимым с JavaWeb-браузером. Апплет — это, фактически, крошечная программа Java, динамически загружаемая через сеть, подобная изображению, звуковому файлу, или видеоклипу. Важное отличие заключается в том, что апплет является интеллектуальной программой, а не просто мультипликацией (анимацией) или media-файлом. Другими словами, апплет — это программа, которая может реагировать на ввод пользователя и динамически изменять, а не просто выполнять ту же самую мультипликацию или звук много раз.
Многоплатформная среда Web предъявляет экстраординарные требования к программе, потому что та должна выполниться надежно в самых разнообразных системах. Поэтому способности создавать устойчивые программы был дан высокий приоритет в проекте Java. Чтобы обеспечить надежность, Java ограничивает вас в нескольких ключевых областях, вынуждая рано находить ошибки при разработке программы. В то же самое время, Java освобождает от необходимости волноваться относительно многих из наиболее общих причин ошибок программирования. Поскольку Java — язык со строгой типизацией, он проверяет ваш код во время компиляции. Однако он также проверяет ваш код и во время выполнения. В действительности, множество трудно прослеживаемых ошибок, которые часто обнаруживаются в трудно воспроизводимых ситуациях во временя выполнения, просто невозможно создать в Java. Знание того, что программа, которую вы написали, будет вести себя предсказуемым образом при разных условиях, является ключевым свойством Java.
Чтобы лучше понимать, насколько устойчив Java, рассмотрим две из главных причин отказа программы: ошибки управления памятью и неуправляемые исключительные состояния (т. е. ошибки во время выполнения). Управление памятью может быть трудной и утомительной задачей в традиционных средах программирования. Например, на C/C++ программист должен вручную распределять и освобождать всю динамическую память. Это иногда ведет к проблемам, потому что программисты или забывают освобождать память, которая была предварительно распределена, или, хуже, пытаются освободить некоторую память, которую другая часть их кода все еще использует. Java фактически устраняет эти проблемы, управляя распределением и освобождением памяти. (Фактически, освобождение полностью автоматическое, потому что Java обеспечивает сборку "мусора" для неиспользованных объектов.) Исключительные состояния в традиционных средах часто возникают в ситуациях типа деления на нуль или "файл, не найден", и они должны управляться неуклюжими и трудно читаемыми конструкциями. Java помогает и в этой области, обеспечивая объектно-ориентированную обработку особых ситуаций. В хорошо написанной Java-программе все ошибки времени выполнения могут — и должны — управляться вашей программой.
Java был спроектирован так, чтобы выполнить реальное требование — создавать интерактивные сетевые программы. Чтобы выполнить это, Java поддерживает многопоточное программирование, которое позволяет вам писать программы, выполняющие одновременно несколько операций. Исполняющая система Java подходит с изящным и все же искушенным решением к синхронизации мультипроцесса, что дает возможность создавать гладко работающие интерактивные системы. Удобный в работе подход Java к многопоточности позволяет вам поразмыслить над спецификой поведения вашей программы, а не заботиться о многозадачной подсистеме.
Программы Java несут в себе существенное количество информации времени выполнения, которая используется, чтобы проверять и разрешать доступ к объектам в период работы программы. Это дает возможность динамически связывать код в безопасной и целесообразной манере, и имеет решающее значение для устойчивости среды апплета, в которой маленькие фрагменты байт-кода могут динамически обновляться исполнительной системой.
Все компьютерные программы состоят из двух элементов: кода и данных. Любая программа может быть концептуально организована либо вокруг ее кода, либо вокруг ее данных. Иначе говоря, некоторые программы концентрируют свою запись вокруг того, "что делается с данными"1
, а другие — вокруг того, "на что этот процесс влияет"2
. Существуют две парадигмы (основополагающих подхода), которые управляют конструированием программ. Первый подход называет программу моделью, которая ориентирована на процесс (process-orientedmodel). При этом подходе программу определяют последовательности операторов ее кода. Модель, ориентированную на процесс, можно представлять как кодовое воздействие на данные (codeactingondata). Процедурные языки, такие как С, успешно эксплуатируют такую модель. Однако, при этом подходе возникают проблемы, когда возрастает размер и сложность программ. Второй подход, названный объектно-ориентированным программированием, был задуман для управления возрастающей сложностью программ. Объектно-ориентированное программирование организует программу вокруг своих данных (т. е. вокруг объектов) и набора хорошо определенных интерфейсов (взаимодействий) с этими данными. Объектно-ориентированную программу можно характеризовать как управляемый данными доступ к коду (datacontrollingaccesstocode). Как вы увидите далее, переключая управление на данные, можно получить некоторые организационные преимущества. Опыт показывает, что отсутствие стандартных базовых библиотек для языка С++ чрезвычайно затрудняет работу с ним. В силу того, что любое нетривиальное приложение требует наличия некоторого набора базовых классов, разработчикам приходится пользоваться различными несовместимыми между собой библиотеками или писать свой собственный вариант такого набора. Все это затрудняет как разработку, так и дальнейшую поддержку приложений, затрудняет стыковку приложений, написанных разными людьми. Полная система Java включает в себя готовый набор библиотек, который можно разбить на следующие пакеты:
· java.lang -- базовый набор типов, отраженных в самом языке. Этот пакет обязательно входит в состав любого приложения. Содержит описания классов Object и Class, а также поддержку многопотоковости, исключительных ситуаций, оболочку для базовых типов, а также некоторые фундаментальные классы.
· java.io -- потоки и файлы произвольного доступа. Аналог библиотеки стандартного ввода-вывода системы UNIX. Поддержка сетевого доступа (sockets, telnet, URL) содержится в пакете java.net.
· java.util -- классы-контейнеры (Dictionary, HashTable, Stack) и некоторые другие утилиты. Кодирование и декодирование. Классы Date и Time.
· java.awt -- Abstract Windowing Toolkit, архитектурно-независимый оконный интерфейс, позволяющий запускать интерактивные оконные Java-приложения на любой платформе. Содержит базовые компоненты интерфейса, такие как события, цвета, фонты, а также основные оконные элементы -- кнопки, scrollbars и т.д.. [6]
4.2 Элементы программирования Java 2 используемые в работе
При реализации метода аппроксимации оператора эволюции средствами языка программирования Java 2, использовались основные элементы объектно-ориентированного программирования, позволяющие разбить программу на более мелкие структурные части, для дальнейшего совершенствования и настраивания ее под различные физические задачи. Использование технологии AWT позволило создать графический интерфейс, наиболее удобный и понятный различному кругу пользователей. В данной работе использовался модуль JSci.math предназначенный для проведения вычислений в специализированных физических и математических задачах. В качестве среды разработки данного программно приложения использовался Eclipse 3.2.
Анимированный апплет позволяет получить наглядное решение нестационарного уравнения Шредингера в различные моменты времени с различными потенциалами. Также выполненный апплет может быть размещен на Internet-сервере и являться частью jsp-странички, что позволит использовать результаты его вычислений различным пользователям сети Internet, используя Internet-браузер для просмотра данной странички.
Программныйкод
public class Shreding {
final double K0 = 1.0;
final double C = 0.893;
double i = Math.sqrt(-1);
double hx = (XMax-XMin)/N;
double hp = 2*PMax/N;
double[] x = new double[N+1];{
Wave ob = new Wave();
x = ob.x();}
double[] p = new double[N+1];{
Wave ob = new Wave();
p = ob.p();}
double[] w = new double[N+1];{
Wave ob = new Wave();
w = ob.w();}
double[] rePsyX0 = new double[N+1];{
Wave ob = new Wave();
rePsyX0 = ob.rePsyX0();}
double[] imPsyX0 = new double[N+1];{
Wave ob = new Wave();
imPsyX0 = ob.imPsyX0();}
double[] psyX02 = new double[N+1];{
Wave ob = new Wave();
psyX02 = ob.psyX02();}
double[] rePsyP0 = new double[N+1];{
Wave ob = new Wave();
rePsyP0 = ob.rePsyP0();}
double[] imPsyP0 = new double[N+1];{
Wave ob = new Wave();
imPsyP0 = ob.imPsyP0();}
double[] rePsyPt2 = new double[N+1];{
Wave ob = new Wave();
rePsyPt2 = ob.rePsyPt2();}
double[] imPsyPt2 = new double[N+1];{
Wave ob = new Wave();
imPsyPt2 = ob.imPsyPt2();}
double[] rePsyX1t2 = new double[N+1];{
Wave ob = new Wave();
rePsyX1t2 = ob.rePsyX1t2();}
double[] imPsyX1t2 = new double[N+1];{
Wave ob = new Wave();
imPsyX1t2 = ob.imPsyX1t2();}
double[] rePsyX1t2V = new double[N+1];{
Wave ob = new Wave();
rePsyX1t2V = ob.rePsyX1t2V();}
double[] imPsyX1t2V = new double[N+1];{
Wave ob = new Wave();
imPsyX1t2V = ob.imPsyX1t2V();}
double[] rePsyP1t = new double[N+1];{
Wave ob = new Wave();
rePsyP1t = ob.rePsyP1t();}
double[] imPsyP1t = new double[N+1];{
Wave ob = new Wave();
imPsyP1t = ob.imPsyP1t();}
double[] rePsyP1te = new double[N+1];{
Wave ob = new Wave();
rePsyP1te = ob.rePsyP1te();}
double[] imPsyP1te = new double[N+1];{
Wave ob = new Wave();
imPsyP1te = ob.imPsyP1te();}
double[] rePsyX2t = new double[N+1];{
Wave ob = new Wave();
rePsyX2t = ob.rePsyX2t();}
double[] imPsyX2t = new double[N+1];{
Wave ob = new Wave();
imPsyX2t = ob.imPsyX2t();}
double[] psyX2t = new double[N+1];{
Wave ob = new Wave();
psyX2t = ob.psyX2t();}
/**
*
* Метод осуществляющий вычисление всех моментов времени
*/
public double[][] time(){
double M[][]= new double[N+1][20+15*(NT+1)];
double L[][]= new double[N+1][NT+1];
for (int m = 0; m < N+1; m++){
M[m][0] = x[m];
M[m][1] = p[m];
M[m][2] = w[m];
M[m][3] = rePsyX0[m];
M[m][4] = imPsyX0[m];
M[m][5] = psyX02[m];
}
for (int k = 1; k < NT+1; k++){
for (int j = 0; j < N+1; j++){
M[j][6+15*(k-1)] = rePsyP0[j];
M[j][7+15*(k-1)] = imPsyP0[j];
M[j][8+15*(k-1)] = rePsyPt2[j];
M[j][9+15*(k-1)] = imPsyPt2[j];
}
for (int m = 0; m < N+1; m++){
M[m][10+15*(k-1)] = rePsyX1t2[m];
M[m][11+15*(k-1)] = imPsyX1t2[m];
M[m][12+15*(k-1)] = rePsyX1t2V[m];
M[m][13+15*(k-1)] = imPsyX1t2V[m];
}
for (int j = 0; j < N+1; j++){
M[j][14+15*(k-1)] = rePsyP1t[j];
M[j][15+15*(k-1)] = imPsyP1t[j];
M[j][16+15*(k-1)] = rePsyP1te[j];
M[j][17+15*(k-1)] = imPsyP1te[j];
}
for (int m = 0; m < N+1; m++){
M[m][18+15*(k-1)] = rePsyX2t[m];
M[m][19+15*(k-1)] = imPsyX2t[m];
M[m][20+15*(k-1)] = psyX2t[m];
rePsyX0 = rePsyX2t;
imPsyX0 = imPsyX2t;
L[m][k] = M[m][20+15*(k-1)];
}
}return L;
}
}
class Wave{
final double K0 = 1.0;
final double C = 0.893;
double i = Math.sqrt(-1);
double hx = (XMax-XMin)/N;
double hp = 2*PMax/N;
/**
*
* Вычисление координат x
*/
double[] x(){
double X[] = new double[N+1];
for (int j = 0; j < N+1; j++){
X[j] = XMin+j*hx;
}return X;
}
double[] x = new double[N+1];{
x = x();}
**
*
* Вычисление импульсов p
*/
double[] p(){
double P[] = new double[N+1];
for (int j = 0; j < N+1; j++){
P[j] = -1*PMax + j*hp;
}return P;
}
double[] p = new double[N+1];{
p = p();}
/**
*
* Построение потенциального барьера
*/
double[] w(double a, double b, double VMax){
double W[]= new double[N+1];
for (int j = 0; j < N+1; j++){
double V = 0;
if (x[j]>a && x[j]<b){
V = VMax;
}W[j] = V;
}return W;
}
double[] w = new double[N+1];{
w = w();}
/**
*
* Действительная часть функци Psy в начальный момент времени
*/
double[] rePsyX0(){
double RePsyX0[]= new double[N+1];
for (int j = 0; j < N+1; j++){
RePsyX0[j] = C*Math.exp(-x[j]*x[j])*Math.cos(K0*x[j]);
}return RePsyX0;
}
double[] rePsyX0 = new double[N+1];{
rePsyX0 = rePsyX0();}
/**
*
* Мнимая часть функци Psy в начальный момент времени
*/
double[] imPsyX0(){
double ImPsyX0[]= new double[N+1];
for (int j = 0; j < N+1; j++){
ImPsyX0[j] = C*Math.exp(-x[j]*x[j])*Math.sin(K0*x[j]);
}return ImPsyX0;
}
double[] imPsyX0 = new double[N+1];{
imPsyX0 = imPsyX0();}
/**
*
* Вероятность в нвчальный момент времени
*/
double[] psyX02(){
double[] L = new double[N+1];
double[] K = new double[N+1];
double[] PsyX02 = new double[N+1];
L = rePsyX0;
K = imPsyX0;
for (int j = 0; j < N+1; j++){
PsyX02[j] = L[j]*L[j] + K[j]*K[j];
}return PsyX02;
}
double[] psyX02 = new double[N+1];{
psyX02 = psyX02();}
/**
*
* Первое преобразование Фурье и вычисление действительной части функции Psy
*/
double[] rePsyP0(){
double RePsyP0[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += rePsyX0[s]*Math.cos(p[j]*x[s]) + imPsyX0[s]*Math.sin(p[j]*x[s]);
}
RePsyP0[j] = hx*S/Math.sqrt(2*Math.PI);}
//rePsyX0 = rePsyX2t;
//imPsyX0 = imPsyX2t;
return RePsyP0;
}
double[] rePsyP0 = new double[N+1];{
rePsyP0 = rePsyP0();}
/**
*
* Первое преобразование Фурье и вычисление мнимой части функции Psy
*/
double[] imPsyP0(){
double ImPsyP0[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += imPsyX0[s]*Math.cos(p[j]*x[s]) - rePsyX0[s]*Math.sin(p[j]*x[s]);
}
ImPsyP0[j] = hx*S/Math.sqrt(2*Math.PI);}
//rePsyX0 = rePsyX2t;
//imPsyX0 = imPsyX2t;
return ImPsyP0;
}
double[] imPsyP0 = new double[N+1];{
imPsyP0 = imPsyP0();}
/**
*
* Произведение действительной части функции Psy и первой составляющей оператора расщепления
*/
double[] rePsyPt2(){
double RePsyPt2[]= new double[N+1];
for (int j=0; j<N+1; j++){
RePsyPt2[j] = rePsyP0[j]*Math.cos(p[j]*p[j]*DT/2) + imPsyP0[j]*Math.sin(p[j]*p[j]*DT/2);
}return RePsyPt2;
}
double[] rePsyPt2 = new double[N+1];{
rePsyPt2 = rePsyPt2();}
/**
*
* Произведение мнимой части функции Psy и первой составляющей оператора расщепления
*/
double[] imPsyPt2(){
double ImPsyPt2[]= new double[N+1];
for (int j=0; j<N+1; j++){
ImPsyPt2[j] = imPsyP0[j]*Math.cos(p[j]*p[j]*DT/2) - rePsyP0[j]*Math.sin(p[j]*p[j]*DT/2)*0;
}return ImPsyPt2;
}
double[] imPsyPt2 = new double[N+1];{
imPsyPt2 = imPsyPt2();}
/**
*
* Второе преобразование Фурье и вычисление действительной части функции Psy
*/
double[] rePsyX1t2(){
double RePsyX1t2[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += rePsyPt2[s]*Math.cos(p[s]*x[j]) - imPsyPt2[s]*Math.sin(p[s]*x[j]);
}
RePsyX1t2[j] = hp*S/Math.sqrt(2*Math.PI);
}return RePsyX1t2;
}
double[] rePsyX1t2 = new double[N+1];{
rePsyX1t2 = rePsyX1t2();}
/**
*
* Второе преобразование Фурье и вычисление мнимой части функции Psy
*/
double[] imPsyX1t2(){
double ImPsyX1t2[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += imPsyPt2[s]*Math.cos(p[s]*x[j]) + rePsyPt2[s]*Math.sin(p[s]*x[j]);
}
ImPsyX1t2[j] = hp*S/Math.sqrt(2*Math.PI);
}return ImPsyX1t2;
}
double[] imPsyX1t2 = new double[N+1];{
imPsyX1t2 = imPsyX1t2();}
/**
*
* Произведение действительной части функции Psy и второй составляющей оператора расщепления
*/
double[] rePsyX1t2V(){
double RePsyX1t2V[]= new double[N+1];
for (int j=0; j<N+1; j++){
RePsyX1t2V[j] = rePsyX1t2[j]*Math.cos(w[j]*DT) + imPsyX1t2[j]*Math.sin(w[j]*DT);
}return RePsyX1t2V;
}
double[] rePsyX1t2V = new double[N+1];{
rePsyX1t2V = rePsyX1t2V();}
/**
*
* Произведение мнимой части функции Psy и второй составляющей оператора расщепления
*/
double[] imPsyX1t2V(){
double ImPsyX1t2V[]= new double[N+1];
for (int j=0; j<N+1; j++){
ImPsyX1t2V[j] = imPsyX1t2[j]*Math.cos(w[j]*DT) - rePsyX1t2[j]*Math.sin(w[j]*DT);
}return ImPsyX1t2V;
}
double[] imPsyX1t2V = new double[N+1];{
imPsyX1t2V = imPsyX1t2V();}
/**
*
* Третье преобразование Фурье и вычисление действительной части функции Psy
*/
double[] rePsyP1t(){
double RePsyP1t[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += rePsyX1t2V[s]*Math.cos(p[j]*x[s]) + imPsyX1t2V[s]*Math.sin(p[j]*x[s]);
}
RePsyP1t[j] = hx*S/Math.sqrt(2*Math.PI);
}return RePsyP1t;
}
double[] rePsyP1t = new double[N+1];{
rePsyP1t = rePsyP1t();}
/**
*
* Третье преобразование Фурье и вычисление мнимой части функции Psy
*/
double[] imPsyP1t(){
double ImPsyP1t[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += imPsyX1t2V[s]*Math.cos(p[j]*x[s]) - rePsyX1t2V[s]*Math.sin(p[j]*x[s]);
}
ImPsyP1t[j] = hx*S/Math.sqrt(2*Math.PI);
}return ImPsyP1t;
}
double[] imPsyP1t = new double[N+1];{
imPsyP1t = imPsyP1t();}
/**
*
* Произведение действительной части функции Psy и третьей составляющей оператора расщепления
*/
double[] rePsyP1te(){
double RePsyP1te[]= new double[N+1];
for (int j=0; j<N+1; j++){
RePsyP1te[j] = rePsyP1t[j]*Math.cos(p[j]*p[j]*DT/2) + imPsyP1t[j]*Math.sin(p[j]*p[j]*DT/2);
}return RePsyP1te;
}
double[] rePsyP1te = new double[N+1];{
rePsyP1te = rePsyP1te();}
/**
*
* Произведение мнимой части функции Psy и третьей составляющей оператора расщепления
*/
double[] imPsyP1te(){
double ImPsyP1te[]= new double[N+1];
for (int j=0; j<N+1; j++){
ImPsyP1te[j] = imPsyP1t[j]*Math.cos(p[j]*p[j]*DT/2) - rePsyP1t[j]*Math.sin(p[j]*p[j]*DT/2);
}return ImPsyP1te;
}
double[] imPsyP1te = new double[N+1];{
imPsyP1te = imPsyP1te();}
/**
*
* Четвертое преобразование Фурье и вычисление действительной части функции Psy
*/
double[] rePsyX2t(){
double RePsyX2t[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += rePsyP1te[s]*Math.cos(p[s]*x[j]) - imPsyP1te[s]*Math.sin(p[s]*x[j]);
}
RePsyX2t[j] = hp*S/Math.sqrt(2*Math.PI);
}return RePsyX2t;
}
double[] rePsyX2t = new double[N+1];{
rePsyX2t = rePsyX2t();}
/**
*
* Четвертое преобразование Фурье и вычисление мнимой части функции Psy
*/
double[] imPsyX2t(){
double ImPsyX2t[]= new double[N+1];
for (int j=0; j<N+1; j++){
double S = 0;
for (int s=0; s<N+1; s++){
S += imPsyP1te[s]*Math.cos(p[s]*x[j]) + rePsyP1te[s]*Math.sin(p[s]*x[j]);
}
ImPsyX2t[j] = hp*S/Math.sqrt(2*Math.PI);
}return ImPsyX2t;
}
double[] imPsyX2t = new double[N+1];{
imPsyX2t = imPsyX2t();}
/**
*
* Вычисление вероятности в момент DT
*/
double[] psyX2t(){
double[] L = new double[N+1];
double[] K = new double[N+1];
double[] PsyX2t = new double[N+1];
L = rePsyX2t;
K = imPsyX2t;
for (int j = 0; j < N+1; j++){
PsyX2t[j] = L[j]*L[j] + K[j]*K[j];
}return PsyX2t;
}
}
Графики поведения волновых функций
Прямоугольный потенциальный барьер




Барьер гауссова функция




Заключение
Численное решение нестационарного уравнения Шредингера имеет важное значение для компьютерного исследования квантовых систем. В данной работе рассмотрены два метода численного решения одномерного нестационарного уравнения Шредингера: метод конечных разностей и метод аппроксимации оператора эволюции. По результатам вычислений построены графики поведения волновой функции в зависимости от времени для ступенчатого потенциала.
Полученные значения полностью соответствуют теоретическим данным для квантовомеханической задачи со ступенчатым потенциалом и наглядно отражают процессы отражения и прохождения частицы через потенциальный барьер. Также рассмотренные численные методы могут использоваться для расчета других видов волновых функций и потенциалов.
Список использованных источников
1. А.С. Давыдов. Квантовая механика//М.,: "Наука", 1973г., 704 с
2. З. Флюгге. Задачи по квантовой механике//М.: "Мир", Т.1, 1974г., 343 с
3. Е.А. Волкова, А.М. Попов, А.Т. Рахимов, "Квантовая механика на персональном компьютере"//Москва.: "УРСС", 1995.
4. Дж. Мэтьюз, Р. Уокер "Математические методы физики".
4. С.В. Поршнев Моделирование квантовых систем //www.exponenta.ru
6. П.Ноутон, Г.Шилдт Java 2 Наиболее полное руководство//С-Петербург: "БХВ-Петербург" 2007.
|