Курсова робота
"Вивчення систем з постійною парною частиною"
Зміст
Введення
1. Парні й непарні вектор-функції
2.Основні відомості з теорії функцій, що відбивають
3. Системи парна-непара
4. Побудова прикладів систем, парна частина загального рішення яких постійна
5. Прості й найпростіші системи
6. Побудова множини систем, парна частина загального рішення яких постійна
6.1 Системи, що мають постійну парну частину
6.2 Побудова систем із заданою парною частиною
Висновок
Список джерел
Введення
При вивченні питань існування періодичних рішень диференціальних систем і рівнянь використовуються властивості симетричності (парність, непарність і т.п.) як функцій, що задають досліджувану систему, так і самих рішень.
У даній роботі ми будемо розглядати сімейства рішень із постійною парною частиною, тобто коли парна частина буде представлена у вигляді константи.
Розберемо приклади систем, сімейства рішень яких мають постійну парну частину. Будемо вивчати побудову систем із заданою парною частиною.
1.
Парні й непарні вектор-функції
За аналогією з функціями одної змінної, вектор-функцію 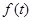 , ,  будемо називати парною (непарної), якщо для всіх будемо називати парною (непарної), якщо для всіх 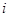 , , 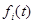 є парною (непарної) функцією, тобто область визначення є парною (непарної) функцією, тобто область визначення  симетрична щодо нуля й симетрична щодо нуля й  ( ( ). ).
Будь-яку функцію із симетричною областю визначення, можна представити як суму парної й непарної функцій. Дійсно, якщо



і 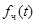 є парною функцією, а є парною функцією, а  – непарної. – непарної.
 будемо називати парною частиною функції будемо називати парною частиною функції  , ,  – непарної. – непарної.
Відзначимо наступні властивості парних і непарних функцій.
Властивість 1 Похідна парної (непарної) функції є функція непарна (парна).
Доказ. a)  – парна функція. – парна функція.
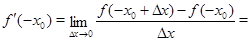


Т.к. 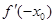 і і 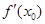 існують або не існують одночасно, те існують або не існують одночасно, те , , 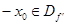 і і  . Таким чином, похідна парної функції є функція непарна. . Таким чином, похідна парної функції є функція непарна.
б)  – непарна функція. – непарна функція.
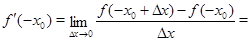

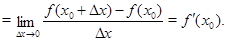
Т.к. 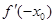 і і 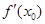 існують або не існують одночасно, те існують або не існують одночасно, те , , 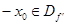 і і  . Таким чином, похідна непарної функції є функція парна. . Таким чином, похідна непарної функції є функція парна.
Властивість 2
Якщо 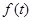 – непарна функція, те – непарна функція, те  . .
Доказ. Оскільки  – непарна функція, те – непарна функція, те

Підставивши замість   одержуємо одержуємо
Звідки треба
2.
Основні відомості з теорії функцій, що відбивають
Розглянемо систему
 (1) (1)
уважаючи, що її права частина безперервна й має безперервні частки похідні по  . Загальне рішення цієї системи у формі Коші позначимо через . Загальне рішення цієї системи у формі Коші позначимо через  . Через . Через  позначимо інтервал існування рішення позначимо інтервал існування рішення 
Нехай
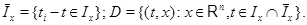
Визначення: функцією, що відбиває, (1) системи назвемо функцію

обумовлену формулою
 (2) (2)
або формулами

Для функції, що відбиває, справедливі властивості:
1) Для будь-якого рішення

системи (1) вірна тотожність
 (3) (3)
2) Для функції, що  відображає, будь-якої системи виконані тотожності: відображає, будь-якої системи виконані тотожності:
 (4) (4)
3) Диференцюєма функція
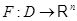
буде функцією, що відбиває, (1) системи тоді й тільки тоді, коли вона задовольняє рівнянням у частинних похідних
 (5) (5)
і початковій умові
 (6) (6)
Рівняння (5) будемо називати основним рівнянням (основним співвідношенням) для функції, що відбиває.
Доказ. Властивість 1) треба безпосередньо з визначення (2). Для доказу властивості 2) помітимо, що відповідно до властивості 1) для будь-якого рішення  системи (1) вірні тотожності системи (1) вірні тотожності
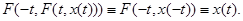
Із цих тотожностей у силу того, що через кожну крапку  проходить деяке рішення проходить деяке рішення  системи (1), і випливають тотожності (5). системи (1), і випливають тотожності (5).
Приступимося до доказу властивості 3). Нехай  – функція, що відбиває, (1)системи . Тоді для неї вірна тотожність (3). Диференціюємо цю тотожність по – функція, що відбиває, (1)системи . Тоді для неї вірна тотожність (3). Диференціюємо цю тотожність по  й скористаємося тим, що й скористаємося тим, що  – рішення системи (1), і самою тотожністю (3). Одержимо тотожність – рішення системи (1), і самою тотожністю (3). Одержимо тотожність
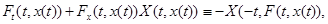
з якого в силу довільності рішення  треба, що треба, що  – рішення системи (5). Початкова умова відповідно до властивості 2) так само виконується. – рішення системи (5). Початкова умова відповідно до властивості 2) так само виконується.
Нехай деяка функція  задовольняє системі (5) й умові (6). Тому що цій системі й цій умові задовольняє так само й функція, що відбиває, то з одиничності рішення (5) задачі (6) - задовольняє системі (5) й умові (6). Тому що цій системі й цій умові задовольняє так само й функція, що відбиває, то з одиничності рішення (5) задачі (6) -  функція повинна збігатися з функцією, що відбиває. Властивість 3) доведено. функція повинна збігатися з функцією, що відбиває. Властивість 3) доведено.
Лема Основна лема 3 Нехай права частина системи (1)  -періодична по -періодична по  , безперервна й має безперервні частки похідні по змінним , безперервна й має безперервні частки похідні по змінним  . Тоді відображення за період для системи (1) можна знайти по формулі . Тоді відображення за період для системи (1) можна знайти по формулі

і тому рішення
системи (1) буде  - періодичним тоді й тільки тоді, коли - періодичним тоді й тільки тоді, коли  є рішення недиференціальної системи є рішення недиференціальної системи
 (7) (7)
Як наслідок цієї леми доведемо наступне припущення.
Твердження 4
Нехай безупинно диференцюєма функція   -періодична й нечетна по -періодична й нечетна по  , тобто , тобто
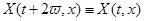
и. 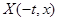 Тоді всяке продовження на відрізок Тоді всяке продовження на відрізок  рішення системи (1) буде рішення системи (1) буде  -періодичним і парним по -періодичним і парним по  . .
Доказ. Для доказу досить помітити, що функція  задовольняє рівнянню (5) й умові (6). Тому вона відповідно до властивості 3) є функцією, що відбиває, розглянутої системи. Рівняння (7) в нашім випадку вироджується в тотожність, і йому задовольняє кожне задовольняє рівнянню (5) й умові (6). Тому вона відповідно до властивості 3) є функцією, що відбиває, розглянутої системи. Рівняння (7) в нашім випадку вироджується в тотожність, і йому задовольняє кожне  , для якого визначене значення , для якого визначене значення

Відповідно до основної леми будь-яке рішення системи (1) буде  -періодичним. Парність довільного рішення -періодичним. Парність довільного рішення  системи (1) треба з тотожностей системи (1) треба з тотожностей

справедливих у силу властивості 1) функції, що відбиває.
Справедливі наступні твердження [4].
Теорема 5 Нехай всі рішення системи (1)  -періодичні й однозначно визначаються своїми початковими даними. Тоді, що відбиває функція, -періодичні й однозначно визначаються своїми початковими даними. Тоді, що відбиває функція,  цієї системи цієї системи  -періодична по -періодична по 
Теорема 6 Нехай система (1)  -періодична по -періодична по  а її рішення однозначно визначаються своїми початковими даними й існують при всіх а її рішення однозначно визначаються своїми початковими даними й існують при всіх  Якщо, крім того, що відбиває функція цієї системи Якщо, крім того, що відбиває функція цієї системи  -періодична по -періодична по  те всі рішення системи (1) періодичні з періодом те всі рішення системи (1) періодичні з періодом 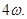
Аналогічна теорема має місце в тому випадку, коли не всі рішення системи (1) продовжимі на відрізок  При цьому висновок про При цьому висновок про  -періодичність можна зробити лише для тих рішень, які існують при всіх -періодичність можна зробити лише для тих рішень, які існують при всіх 
З  -періодичності функції, що відбиває, -періодичності функції, що відбиває,  треба -періодичність всіх продовжимих треба -періодичність всіх продовжимих  на рішення періодичної (1)системи . З на рішення періодичної (1)системи . З  -періодичності функції, що відбиває, не треба, загалом кажучи -періодичності функції, що відбиває, не треба, загалом кажучи , -періодичність , -періодичність  рішень -періодичної системи, хоча треба рішень -періодичної системи, хоча треба  їх -періодичність. їх -періодичність.
Не слід думати, що якщо всі рішення  -періодичної системи -періодичної системи  -періодичні, те її функція, що відбиває, зобов'язана -періодичні, те її функція, що відбиває, зобов'язана  бути -періодичної. Цьому суперечить приклад рівняння бути -періодичної. Цьому суперечить приклад рівняння 
У випадку, коли  , тобто коли система (1) вироджується в рівняння, вірна , тобто коли система (1) вироджується в рівняння, вірна
Теорема 7 Нехай рівняння (1)  -періодичне по -періодичне по  а його рішення однозначно визначаються своїми початковими даними й існують при всіх а його рішення однозначно визначаються своїми початковими даними й існують при всіх  Тоді для того, щоб всі рішення рівняння (1) були Тоді для того, щоб всі рішення рівняння (1) були  -періодичні, необхідна й достатня -періодичні, необхідна й достатня  -періодичність по -періодичність по  функції, що відбиває, цього рівняння. функції, що відбиває, цього рівняння.
3.
Системи парна-непара
Розглянемо систему
 (8) (8)
Будемо вважати, що всюди надалі ця система задовольняє умовам:
а) Функція  безупинно диференцюєма, і тому, задача Коші для системи (8) має єдине рішення; безупинно диференцюєма, і тому, задача Коші для системи (8) має єдине рішення;
б) Права частина системи (8)  -періодична по -періодична по  . .
Лема 8
Нехай система (8) задовольняє умовам а) і б). Тоді продовжині на відрізок  рішення рішення  цієї системи буде цієї системи буде  -періодичним тоді й тільки тоді, коли -періодичним тоді й тільки тоді, коли
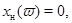

– є непарна частина рішення  . .
Доказ. Нехай  – –  -періодичне рішення системи (8). Тоді -періодичне рішення системи (8). Тоді

Необхідність доведена.
Нехай  – рішення системи (8), для якого – рішення системи (8), для якого  . Тоді . Тоді
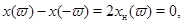
і тому

Таким чином, крапка  є нерухлива крапка відображення за період, а рішення є нерухлива крапка відображення за період, а рішення  – –  -періодичне. -періодичне.
Доведена лема, питання про періодичність рішення

зводить до обчислення одного зі значень непарної частини  . Іноді відносно . Іноді відносно  можна сказати більше, ніж про саме рішення можна сказати більше, ніж про саме рішення  . Це дозволяє в таких випадках робити різні висновки щодо існування періодичних рішень у систем виду (8). Диференцуємі функції . Це дозволяє в таких випадках робити різні висновки щодо існування періодичних рішень у систем виду (8). Диференцуємі функції


задовольняють деякій системі диференціальних рівнянь. Перш, ніж виписати цю систему, помітимо:
 (9) (9)
тому що

рішення системи (8). Заміняючи в тотожності (9)  на на  й з огляду на, що похідна парної функції – функція непарна, а похідна непарної функції – функція парна, одержуємо тотожність й з огляду на, що похідна парної функції – функція непарна, а похідна непарної функції – функція парна, одержуємо тотожність
 (10) (10)
З тотожностей (9) і (10) знайдемо похідні:

У такий спосіб вектор-функція
 (11) (11)
задовольняє наступній системі диференціальних рівнянь порядку 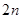 : :
 (12) (12)

Систему (12) будемо називати системою пар-непара, що відповідає системі (8). рішення системи чіт-непара, як треба з умови а), однозначно визначається своїми початковими умовами.
4.
Побудова прикладів систем, парна частина загального рішення яких постійна
Приклад

Знайдемо рішення: будемо використовувати метод виключення, візьмемо перше рівняння системи й виразимо з нього  : :
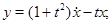
тепер диференціюємо його

Ми можемо дорівняти ліву частину отриманого рівняння з лівою частиною другого рівняння вихідної системи

Зробимо перетворення й приведемо подібні




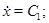

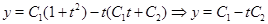
У такий спосіб:
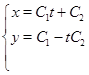
Зробимо перевірку, для цього у вихідну систему підставимо отримане рішення:

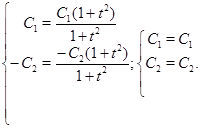
Одержали вірні рівності. Значить було знайдено правильне рішення вихідної системи.
Парна частина загального рішення:
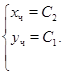
Приклад
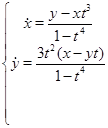
Знайдемо рішення: будемо використовувати метод виключення, візьмемо перше рівняння системи й виразимо з нього  : :

тепер диференціюємо його
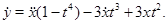
Ми можемо дорівняти ліву частину отриманого рівняння з лівою частиною другого рівняння вихідної системи

Зробимо перетворення й приведемо подібні

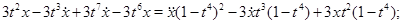


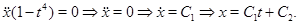

У такий спосіб:
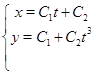
Зробимо перевірку:



Парна частина загального рішення

Приклад

Знайдемо рішення: будемо використовувати метод виключення, візьмемо перше рівняння системи й виразимо з нього  : :

тепер диференціюємо його
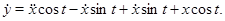
Ми можемо дорівняти ліву частину отриманого рівняння з лівою частиною другого рівняння вихідної системи

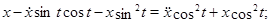


Одержали два рішення  й й  . .
1) 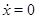 ; ;
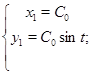
2)  ; ;
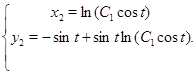
Зробимо перевірку для  : :




Одержали вірні рівності. Значить було знайдено правильне рішення вихідної системи.
Зробимо перевірку для  : :

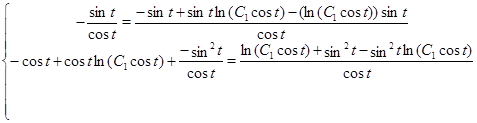

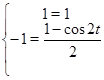

Звідси видно, що  не є рішенням для вихідної системи. не є рішенням для вихідної системи.
У такий спосіб:

Парна частина загального рішення
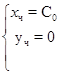
З даних прикладів можемо помітити, що рішення систем записується у вигляді:
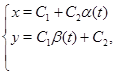
де 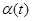 й й  – непарні функції, а парна частина представлена константою. – непарні функції, а парна частина представлена константою.

 ; ;
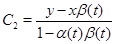 ; ;
 (13) (13)
Системи виду (13) будуть мати сімейства рішень із постійною парною частиною. У цьому легко переконається, проробивши обчислення, аналогічні попереднім прикладам.
5.
Прості й найпростіші системи
Лема 9
Для всякої безупинно диференцюємої функції

для якої виконані тотожності (4), мають місце співвідношення
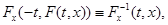

Теорема 10
Для всякої двічі безупинно диференцюємої функції  певної в симетричній області певної в симетричній області 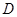 , що містить гіперплощина , що містить гіперплощина  для якої виконані тотожності (4), існує диференціальна система для якої виконані тотожності (4), існує диференціальна система  c безупинно диференцюємої правою частиною, що відбиває функція якої збігається с. c безупинно диференцюємої правою частиною, що відбиває функція якої збігається с.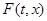
Теорема 11
Для всякої двічі безупинно диференцюємої функції

певної в області  утримуюча гіперплощина утримуюча гіперплощина 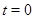 , для якої виконані тотожності (4), при всіх , для якої виконані тотожності (4), при всіх  і досить малих і досить малих  існує диференціальна система існує диференціальна система

функція, що відбиває, якої збігається  з а загальний інтеграл задається формулою з а загальний інтеграл задається формулою

Наслідок 12 Двічі безупинно диференцюєма функція
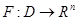
є функцією, що відбиває, хоча б однієї диференціальної системи тоді й тільки тоді, коли для неї виконані (4)тотожності .
Системи, існування яких гарантується теоремами 10 й 11, називаються відповідно простій і найпростішої.
Теорема 13 Нехай
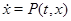
найпростіша система, тоді

де  – функція, що відбиває, (1)системи . – функція, що відбиває, (1)системи .
Доказ. Якщо система найпростіша,
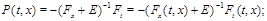

Теорема 14 Нехай

є функція, що відбиває, деякої диференціальної системи, рішення якої однозначно визначаються своїми початковими даними, а для безупинно диференцюємої функції
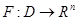
виконано тотожності (4). Тоді для того, щоб в області  функція функція  збігалася з збігалася з  необхідно й досить, щоб розглянута система мала вигляд необхідно й досить, щоб розглянута система мала вигляд

або вид
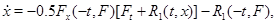
Де
є деяка безперервна вектор-функція.
Будемо говорити, що множина систем виду (1) утворить клас еквівалентності, якщо існує диференцюєма функція

із властивостями:
1) функція, яка відбиває
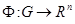
будь-якої системи з розглянутої множини збігається у своїй області визначення  з функцією з функцією 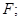
2) Будь-яка система виду (1), що відбиває функція
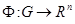
яке збігається в області 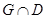 з функцією з функцією  втримується в розглянутій множині. втримується в розглянутій множині.
Дві системи виду (1), що належать одному класу еквівалентності, будемо називати еквівалентними. Допускаючи певну вільність мови, будемо говорити також, що вони мають ту саму функцію, що відбиває. Функцію  при цьому будемо називати функцією, що відбиває, класу, а клас - відповідної функції, що при цьому будемо називати функцією, що відбиває, класу, а клас - відповідної функції, що  відбиває . відбиває .
Із третьої властивості функції, що відбиває, треба, що (1) система й система

належать одному класу еквівалентності тоді й тільки тоді, коли система рівнянь

Сумісна
Необхідною умовою спільності цієї системи є тотожність 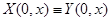 . .
6.
Побудова множини систем, парна частина загального рішення яких постійна
6.1
Системи, що мають постійну парну частину
Нехай нам дана система
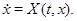 (14) (14)
Перед нами встає наступне питання про те, коли сімейство рішень цієї системи будуть мати постійну парну частину.
 (15) (15)
Тобто, коли  не буде залежати від часу не буде залежати від часу 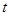 . .
Візьмемо функцію, що відбиває, (14) 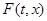 системи й використовуючи системи й використовуючи
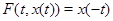
одержимо парну частину в такий спосіб:
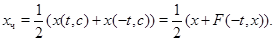 (16) (16)
Теорема 15 Якщо виконано тотожність
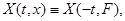
де  – функція, що відбиває, для лінійної системи (14)виду , те будь-яке рішення цієї системи має постійну парну частину. – функція, що відбиває, для лінійної системи (14)виду , те будь-яке рішення цієї системи має постійну парну частину.
Доказ. Візьмемо будь-яке рішення  системи (14). Його похідна системи (14). Його похідна

Тому можемо записати

З умови теореми маємо
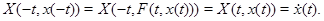
У такий спосіб одержали, що  – парна вектор-функція. Тоді – парна вектор-функція. Тоді

6.2
Побудова систем із заданою парною частиною
Розглянемо систему (14). Будемо будувати систему із заданою парною частиною.
Нехай нам відома парна частина  . Скористаємося формулою (15) й перетворимо її . Скористаємося формулою (15) й перетворимо її

Отже, можемо записати
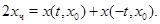
Звідси знаючи (3), одержимо

де  – функція, що відбиває, системи. Крім – функція, що відбиває, системи. Крім  із попереднього співвідношення, з довільною функцією, що із попереднього співвідношення, з довільною функцією, що 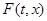 відбиває , задовольняючій умові відбиває , задовольняючій умові

одержимо необхідну систему.
Приклад 16
Нехай

де  – задана парна частина, – задана парна частина,  . Диференціюємо обидві частини рівності . Диференціюємо обидві частини рівності

Перетворимо праву частину
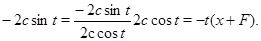
Перепишемо отримане у вигляді:

Виразимо  : :
 (17) (17)
Для всіх систем виду (17) повинне бути виконане умова

Візьмемо
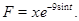
Знайдемо  , ,  . .  ; ;

Підставимо значення  , ,  у систему (17): у систему (17):

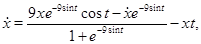

Одержуємо необхідну систему:

Приклад 17
Нехай

де  – задана парна частина, – задана парна частина,  . Диференціюємо обидві частини рівності . Диференціюємо обидві частини рівності
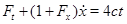
і перетворимо праву частину

Перепишемо отримане у вигляді:

Виразимо  : :
 (18) (18)
Для всіх таких систем повинне бути виконане умова  . .
Візьмемо  . Знайдемо . Знайдемо  , ,  . .  , ,
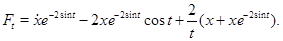
Підставимо знайдені значення в систему (18) й зробивши перетворення аналогічні прикладу 16, одержуємо:
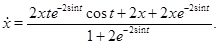
Розглянемо тепер загальний випадок, коли нам задана парна частина  загального рішення системи з функцією, що загального рішення системи з функцією, що 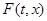 відбиває . У цьому випадку відбиває . У цьому випадку
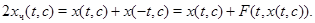
Тому, якщо  нам задана, то зі співвідношення нам задана, то зі співвідношення
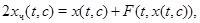
при заданій  ми знайдемо загальне рішення ми знайдемо загальне рішення  шуканої системи. Саму систему ми побудуємо крім шуканої системи. Саму систему ми побудуємо крім  зі співвідношень зі співвідношень

Таким чином, ми прийшли до
Теорема 18
Усяка система
 (19) (19)
де  перебувають із системи перебувають із системи
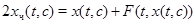
при будь-якої заданої диференціюємої функції 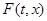 , що задовольняє співвідношенням , що задовольняє співвідношенням

має загальне рішення з парною частиною  . .
Якщо
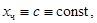
те система (19) має вигляд:
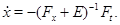
Таким чином, ми прийшли до висновку:
Наслідок 19
Загальне рішення диференціальної системи має постійну парну частину тоді й тільки тоді, коли ця система найпростіша.
Висновок
Основним результатом даної роботи є побудова диференціальних систем, сімейство рішень яких має задану парну частину. А так само теорема про зв'язок найпростішої системи й системи, сімейство рішень якої має постійну парну частину.
Теорема. Загальне рішення диференціальної системи має постійну парну частину тоді й тільки тоді, коли ця система найпростіша.
Список джерел
[1]
Арнольд В.І., Звичайні диференціальні рівняння. – К., 2004
[2]
Бібіков Ю.Н., Загальний курс диференціальних рівнянь. – К., 1999
[3]
Еругин Н.П., Книга для читання за загальним курсом диференціальних рівнянь.3-е видання. – К., 2000
[4]
Мироненко В.И., Функція й періодичні рішення диференціальних рівнянь. – К., 2004
[5]
Понтрягин Л.С., Звичайні диференціальні рівняння. – К., 2003
|