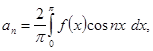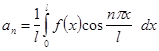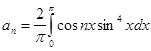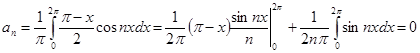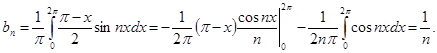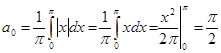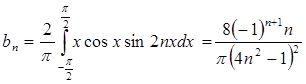Курсовая работа: Вивчення функцій рядів Фур'є
|
Название: Вивчення функцій рядів Фур'є Раздел: Рефераты по математике Тип: курсовая работа |
Курсова робота Вивчення функцій рядів Фур'є Зміст 1. Визначення коефіцієнтів по методу Ейлера-Фур'є 2. Ортогональні системи функцій 3. Інтеграл Дирихле. Принцип локалізації 4. Подання функцій рядом Фур'є 5. Випадок неперіодичної функції 6. Випадок довільного проміжку 7. Випадок парних і непарних функцій 8. Приклади розкладання функцій у ряд Фур'є Список використаної літератури Введення У науці й техніку часто доводитися мати справу з періодичними явищами, тобто такими, які відтворюються в колишньому виді через певний проміжок часу Т, що називається періодом. Наприклад, рух парової машини повторюється, після того як пройде повний цикл. Різні величини, пов'язані з періодичним явищем, після закінчення періоду Т вертаються до своїх колишніх значень і являють собою періодичні функції від часу t з періодом Т.
Якщо не вважати постійної, то найпростішою періодичною функцією є синусоїдальна величина:
З подібних найпростіших періодичних функцій можуть бути складені й більше складні. Ясно, що тридцятимільйонні синусоїдальні величини повинні бути різних частот, інакше їхнє додавання не дає нічого нового, а знову приводить до синусоїдальної величини, причому тієї ж частоти. Якщо ж скласти величини виду:
які мають різні частоти
те вийде періодична функція, але вже що істотно відрізняється від величин, що входять у суму. Розглянемо для приклада додавання трьох синусоїдальних величин:
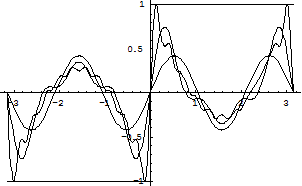
На малюнку ми бачимо, що графік функції отриманої в результаті додавання трьох синусоїдальних величин (показаний суцільною лінією) уже значно відрізняється від синусоїди. Більшою мірою це має місце для суми нескінченного ряду величин виду (1). Тепер виникає зворотне питання: чи можна дану періодичну функцію представити у вигляді суми кінцевої або нескінченної множини синусоїдальних величин виду (1). Як буде показано нижче, на це питання можна відповісти задовільно, але тільки лише використовуючи нескінченну послідовність величин виду (1). Для функцій деякого класу має місце розкладання в "тригонометричний ряд":
З геометричної точки зору це означає, що графік періодичної функції виходить шляхом накладення ряду синусоїд. Якщо ж кожну синусоїдальну величину витлумачити механічно що як представляє гармонійні коливальні явища, то можна сказати, що тут складне коливання розкладається на окремі гармонійні коливання. Виходячи із цього, окремі синусоїдальні величини, що входять до складу розкладання (2), називають гармонійними функції Якщо за незалежну змінну вибрати
те вийти функція, що залежить від х, так само періодична, але вже зі стандартним періодом
Тепер розгорнувши члени цього ряду по формулі синуса суми й позначивши
ми прийдемо до остаточної форми тригонометричного розкладання:
У даному розкладанні функція від кута х, що має період Ми прийшли до розкладання функції в тригонометричний ряд, відправляючись від періодичних, коливальних явищ і пов'язаних з ними величин. Подібні розкладання часто виявляються корисними й при дослідженні функцій, заданих у певному кінцевому проміжку й зовсім не породжених ніякими коливальними явищами. 1. Визначення коефіцієнтів по методу Ейлера-Фур'є У попередньому параграфі було сказано, що існує ряд функцій, які можна представити у вигляді нескінченного тригонометричного ряду. Для того, що б установити можливість розкладання деякої функції
потрібно мати набір коефіцієнтів Прийом для знаходження цих коефіцієнтів у другій половині XVIII століття був застосований Ейлером і незалежно від нього на початку XIX Фур'є.Надалі будемо припускати функцію
Але, як легко бачити,
Тому всі члени під знаком суми будуть рівнятися нулю, і остаточно одержуємо
Для того щоб знайти значення коефіцієнта
У виді (5)
якщо
Таким чином, звертаються в нуль всі інтеграли під знаком суми, крім інтеграла, при якому множником є саме коефіцієнт
Аналогічно, множачи розкладання (4) на
Формули, по яких обчислюються коефіцієнти Дамо тепер звіт у тім, яка логічна цінність проведених міркувань. Ми виходили з того, що тригонометричний ряд (4) має місце, тому питання про те, чи відповідає це дійсності, залишається відкритим. Ми користувалися повторно по членним інтегруванням ряду, а ця операція не завжди можна, достатньою умовою для застосування операції є рівномірна збіжність ряду. Тому строго встановленою умовою можна вважати лише наступне: якщо функція f(x) розкладається в рівномірно збіжний тригонометричний ряд (4), то цей ряд буде її поруч Фур'є. Якщо ж не припускати наперед рівномірності збіжності, то всі наведені вище міркування не доводять навіть того, що функція може розкладатися тільки в ряд Фур'є. Ці міркування можна розглядати лише як наведення, достатнє для того, щоб у пошуках тригонометричного розкладання даної функції почати її з ряду Фур'є, зобов'язуючись установити умови, при яких він сходиться й притім саме до даної функції. Поки цього не зроблено, ми маємо право лише формально розглядати ряд Фур'є даної функції, але не можемо про нього нічого затверджувати, крім того, що він "породжений" функцією f(x). Цей зв'язок звичайно позначають так:
уникаючи знака рівності. 2. Ортогональні системи функцій Дві функції
Розглянемо систему функцій
те неї називають ортогональною системою функцій. При цьому завжди будемо думати, що
Якщо Найважливішим прикладом ортогональної системи функцій саме і є тригонометрична система
у проміжку
Нехай у проміжку
Для визначення коефіцієнтів даного розкладання надійдемо так само, як ми це зробили в попередньому параграфі, а саме помножимо обидві частини рівності на
У силу ортогональності системи, всі інтеграли праворуч, крім одного, будуть дорівнюють нулю, і легко виходить:
Ряд (11) з коефіцієнтами, складеними по формулах (12), називається узагальненим рядом Фур'є даної функції, а самі коефіцієнти-її узагальненими коефіцієнтами Фур'є щодо системи
У даному випадки всі зауваження зроблені в попередньому параграфі необхідно повторити. Узагальнений ряд Фур'є, побудований для функції
Збіжність цього ряду, як і у випадку тригонометричного ряду, підлягає ще дослідженню. 3. Інтеграл Дирихле Принцип локалізації Нехай
і по них складемо ряд Фур'є нашої функції
Як бачимо, тут коефіцієнт Якщо функція F(x) кусочно-безперервна в будь-якому кінцевому проміжку й до того ж має період
по колишньому проміжку довжини Дійсно, маємо
Якщо в останньому інтеграла зробити підстановку
і лише знаком буде відрізнятися від першого інтеграла. Таким чином, розглянутий інтеграл виявляється рівним інтегралу
уже не утримуючому Для того щоб досліджувати поводження ряду в якій-небудь певній крапці
Підставимо замість
Легко перевірити тотожність
Скористаємося цією тотожністю для перетворення вираження, остаточно одержимо
Цей інтеграл називають інтегралом Дирихле, хоча у Фур'є він зустрічається набагато раніше. Тому що ми маємо справу з функцією від u періоду
Підстановкою
Потім, розбиваючи інтеграл на два:
Таким чином, справа зводиться до дослідження поводження саме цього інтеграла, що містить параметр n. Для подальшого викладу матеріалу нам буде потрібно одна лема, що належить Риману, що ми залишимо без доказу. Якщо функція
і, аналогічно,
Якщо згадати формули, що виражають коефіцієнти Фур'є Коефіцієнти Фур'є Другим безпосереднім наслідком є так званий "принцип локалізації". Взявши довільне позитивне число
те стане ясно, що множник при синусі
є кусочно-безперервною функцією від t у проміжку
Але в цей інтеграл входять лише значення функції f(x), що відповідають зміні аргументу в проміжку від Поводження ряду Фур'є функції f(x) у деякій крапці Таким чином, якщо взяти дві функції, значення яких у довільно малій околиці 4. Подання функцій рядів Фур'є Накладемо на функцію f(x) більше важка вимога, а саме-припустимо її у проміжку Тоді має місце загальна теорема: Теорема. Якщо функція f(x) з періодом
Ця сума, мабуть, дорівнює Доказ. Відзначимо, що рівність (14) має місце для кожної функції f(x), що задовольняє поставленим умовам. Якщо, зокрема, взяти
Множачи обидві частини рівності на постійне число
для нашої мети потрібно довести, що інтеграл праворуч при Представимо його у вигляді
де покладено
якби нам удалося встановити що ця функція кусочно-безперервна, то з леми попереднього параграфа варто було б уже, що інтеграл (15) має межу нулю при Ми доведемо існування кінцевої межі
поклавши тоді g(0)=K, ми в крапці t=0 одержимо безперервність, і застосування леми виявиться виправданим. Але другий множник у правій частині рівності (16) явно має межею одиницю; звернемося до вираження квадратних дужках. Нехай, для простати, спочатку крапка
прагне до межі Отже, наш висновок справедливо у всіх випадках. 5. Випадок неперіодичної функції Вся побудована вище теорія виходила із припущення, що задана функція визначена для всіх речовинних значень x і притім має період Що б мати право застосувати до такої функції викладену теорію, уведемо замість її допоміжну функцію
потім думаємо
а на інші речовинні значення x поширюємо функцію До побудованого в такий спосіб функції Особливої уваги, однак, вимагають кінці проміжку
Таким чином, якщо задана функція
відмінне як від Наступне зауваження так само заслуговує на особливу увагу. Якщо тригонометричний ряд
сходиться в проміжку 6. Випадок довільного проміжку Припустимо, що функція
те вийде функція
коефіцієнти якого визначаються формулами Ейлера-Фур'є:
повернемося тепер до колишньої змінного
Тоді одержимо розкладання заданої функції
Тут косинуси й синуси беруться від кутів, кратних не
Відносно кінців проміжку
7. Випадок парних і непарних функцій Якщо задана в проміжку
У цьому легко переконається:
Таким же шляхом установлюється, що у випадку парної функції
Нехай тепер
Таким чином, ряд Фур'є парної функції містить одні лише косинусів:
Тому що
Якщо ж функція
Ми доходимо висновку, що ряд Фур'є непарної функції містить одні лише синусів:
При цьому через парність добутку
Відзначимо, що кожна функція
Де
Очевидно, що ряд Фур'є функції Припустимо, далі, що функція Можна використовувати сваволю у визначенні функції в проміжку Аналогічно, якщо доповнити визначення функції Таким чином, задану в проміжку Особливого дослідження вимагають крапки
те й при Інакше є справа з розкладанням по синусах. У крапках Якщо функція
або в ряд по синусах
до тільки що розглянутого. При цьому коефіцієнти розкладань обчислюються, відповідно, по формулах
або
8. Приклади розкладання функцій у ряд Фур'є Функції, які нижче приводяться як приклади, як правило, ставляться до класу диференцуємих або кусочно-диференцуємих. Тому сама можливість їхнього розкладання в ряд Фур'є-Поза сумнівом, і на цьому ми зупинятися не будемо. Всі завдання взяті зі Збірника задач і вправ по математичному аналізі, Б. Н. Демидович. № 2636. Функцію Тому що функція Знайдемо коефіцієнти розкладання;
№ 2938. Розкласти в ряд Фур'є функцію
Функція
Тобто, виходить, що при парних значеннях n коефіцієнт Ряд Фур'є для цієї функції прийме наступний вид:
Нижче зображені графіки функцій Графік функції
№ 2940. Функція
№ 2941.
У підсумку одержуємо ряд Фур'є:
№ 2941. Функція
Як і в № 2938, у нас при парних значеннях n коефіцієнт У підсумку одержимо:
№ 2950. Функція
Тому що при n=1 знаменник звертається в нуль, то підсумовування необхідно зробити починаючи у двійки.
№ 2951. Функція
№ 2961. Функцію а)
І, нарешті одержуємо розкладання в ряд Фур'є:
б)
в)
№ 2962 Виходячи з розкладання
По членним інтегруванням одержати розкладання в ряд Фур'є на інтервалі інтегруємо рівність
І остаточно одержуємо:
Інтегруємо отриману рівність повторно
або звідси одержуємо
Список літератури 1.І.М. Уваренков, М.З. Маллер Курс математичного аналізу., - К., 2006 2.Г.М. Фихтенгольц Курс диференціального й інтегрального вирахування. – К., 2005р. 3.В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов Курс вищої математики. – К., 2005 4.Н.Я. Виленкин, В.В. Цукерман, М.А. Доброхотова, А.Н. Сафонов Ряди. – К., 1997 5.Б.П. Демидович Збірник задач і вправ по математичному аналізу. – К., 2005 |

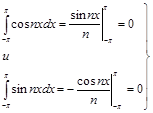 (5)
(5) .
.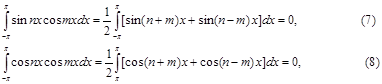
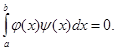
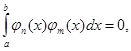

 , що уже свідомо буде нормальною.
, що уже свідомо буде нормальною.
 (m=0, 1, 2, …) (12)
(m=0, 1, 2, …) (12)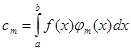






 (13)
(13)

 (14)
(14) . Якщо другий з них переписати у вигляді
. Якщо другий з них переписати у вигляді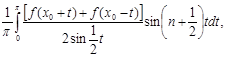

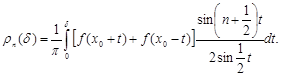
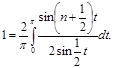

 (15)
(15) (16)
(16)

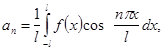
 (20)
(20)
 (20a)
(20a)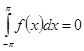
 .
. .
.