Министерство общего и профессионального образования Свердловской области МОУ СОШ №62
Направление: научно – техническое
Секрет возникновения арабских чисел
Исполнители:
Надыршин Дамир Рафаэльевич
Чекасин Егор Романович
Руководитель: Кульчицкая Л.А.
Учитель математики ВКК
МОУ СОШ №62
Екатеринбург, 2011
Введение
Цель работы:
1. Познакомится с цифрами древности:
- Арабскими
- Разных народов
- Китайскими
- Деванагари
- Современными
2. Узнать об Арабских цифрах: их написании, истории и развитии
3. Узнать, почему Арабские цифры удобнее других систем счисления
Мы познакомимся с цифрами разных народов и проследим их развитие от древности, до наших дней. Мы узнаем почему арабская система счисления самая удобная? Как цифры выглядели в древности? Как писались китайские цифры? Как и когда европейцы познакомились с арабскими цифрами? Почему неудобна система счисления Древнего Рима? Это вы узнаете реферате «Секрет возникновения арабских чисел»
1. Арабские цифры
1.1 Секрет возникновения арабских чисел
Традиционное название десяти математических знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С помощью них по десятичной системе счисления записываются любые числа. В течение тысячелетий люди использовали пальцы рук для обозначения числа. Так, один предмет они, так же как и мы, показывали одним пальцем, три – тремя. С помощью руки можно было показать до пяти единиц. Для выражения большего количества использовались обе руки, а в некоторых случаях и обе ноги. Сейчас мы постоянно пользуемся числами. Используем их, чтобы измерять время, покупать и продавать, звонить по телефону, смотреть телевизор, водить автомобиль. К тому же у каждого человека есть различные числа, идентифицирующие лично его. Например, в удостоверении личности, в банковском счете, в кредитной карточке и т.д. Более того, в компьютерном мире вся информация, и этот текст в том числе, передается посредством числовых кодов.
Мы встречаемся с числами на каждом шагу и настолько к ним привыкли, что почти не отдаем себе отчета, насколько важную роль они играют в нашей жизни. Числа составляют часть человеческого мышления. На протяжении истории каждый народ писал числа, считал и вычислял с их помощью. Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около пяти тысяч лет назад. Хотя эти две культуры находились очень далеко друг от друга, их числовые системы очень похожи, как будто представляют один метод – использование засечек на дереве или камне для записи прошедших дней. Египетские жрецы писали на папирусе, а в Месопотамии на мягкой глине. Конечно, конкретные формы их цифр различны, но и в той, и в другой культуре использовали простые черточки для единиц и другие метки для десятков и более высоких порядков. Кроме того, в обеих системах писали желаемую цифру, повторяя черточки и метки нужное число раз.
Были найдены два египетских документа, созданные около четырех тысяч лет назад, с самыми древними математическими записями из обнаруженных до сих пор. Стоит отметить, что это записи именно математического характера, а не просто числовые.
1.2 История
История наших привычных «арабских» чисел очень запутана. Нельзя сказать точно и достоверно как они произошли. Одно точно известно, что именно благодаря древним астрономам, а именно их точным расчетам мы и имеем наши числа. Между II и VI веками н.э. индийские астрономы познакомились с греческой астрономией. Они переняли шестидесятеричную систему и круглый греческий нуль. Индийцы соединили принципы греческой нумерации с десятичной мультипликативной системой взятой из Китая. Так же они стали обозначать цифры одним знаком, как было принято в древнеиндийской нумерации брахми. Блестящая Севильи перевел на латынь эту книгу, и индийская система счета широко распространилась по всей Европе.
Цифры возникли в Индии, не позднее V века. Тогда же было открыто и формализовано понятие нуля (шунья). Арабские цифры возникли в Индии, не позднее V века. Тогда же было открыто и формализовано понятие нуля, которое позволило перейти к позиционной записи. которой Арабские цифры стали известны европейцам в X вв. Благодаря тесным связям христианской Барселоны и мусульманской Кордовы), Сильвестр имел возможность доступа к научной информации, которой не имел никто в тогдашней Европе. В частности он одним из первых среди европейцев познакомился с арабскими цифрами, понял удобство их употребления по сравнению с римскими и начал их внедрять в европейскую науку.
В старых вавилонских текстах, датируемых 1700 годом до нашей эры, не встречается специального знака, обозначающего ноль, для его обозначения просто оставляли пустое место, более или менее выделенное.
1.3 Написание цифр
Написание арабских цифр состояло из отрезков прямых линий, где количество углов соответствовало величине знака. Вероятно, кто-то из арабских математиков когда-то предложил идею - связать числовое значение цифры с количеством углов в ее написании.
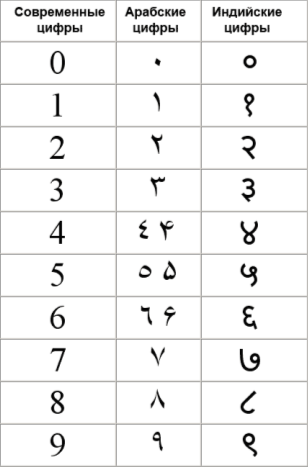
Посмотрим на арабские цифры и видим, что
0 - цифра без единого угла в начертании.
1 - содержит один острый угол.
2 - содержит два острых угла.
3 - содержит три острых угла (правильное, арабское, начертание цифры получается при написании цифры 3 при заполнении почтового индекса на конверте)
4 - содержит 4 прямых угла (именно этим объясняется наличие «хвостика» внизу цифры, никак не влияющего на ее узнаваемость и идентификацию)
5 - содержит 5 прямых углов (назначение нижнего хвостика - то же самое, что у цифры 4 - достройка последнего угла)
6 - содержит 6 прямых углов.
7 - содержит 7 прямых и острых углов (правильное, арабское, написание цифры 7 отличается от приведенного на рисунке наличием дефиса, пересекающего под прямым углом вертикальную линию посередине (вспомним, как мы пишем цифру 7), что дает 4 прямых угла и 3 угла дает еще верхняя ломаная линия)
8 - содержит 8 прямых углов.
9 - содержит 9 прямых углов (именно этим объясняется столь замысловатый нижний хвостик у девятки, который должен был достроить 3 угла, чтобы общее их число стало равно 9.
Вывод
Мы узнали когда и как появились арабские числа, как пишутся, что они из себя представляют и общее значение цифр
2. Цифры разных народов
Арабские цифры используемые в арабских странах Африки
1 2 3 4 5 6 7 8 9 0
◗Индо - арабские цифры
٠١٢٣٤٥٦٧٨٩
◗Цифры в письме ория.
୦୧୨୩୪୫୬୭୮୯
◗Цифры в тибетском письме.
༠༡༢༣༤༥༦༧༨༩
◗Цифры в тайском письме.
๐๑๒๓๔๕๖๗๘๙
◗Цифры в лаосском письме.
໐໑໒໓໔໕໖໗໘໙
Египтяне писали иероглифами, цифры тоже. У египтян были знаки для обозначения чисел от 1 до 10 и специальные иероглифы для обозначения десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов и даже десятков миллионов.Следующий этап в истории числа осуществили древние римляне. Они изобрели систему исчисления, основанную на использовании букв для отображения чисел. Они применяли в своей системе буквы «I», «V», «L», «C», «D», и «M».Каждая буква имела различное значение, каждая цифра соответствовала номеру положения буквы. Для того, чтобы прочесть римскую цифру или написать ее, нужно следовать нескольким основным правилам.
В Центральной Америке в первом тысячелетии нашей эры майя писали любое число, используя лишь три знака: точку, линию и эллипс. Точка имела значение единицы, линия означала пять, комбинация точек и линий служила для написания чисел от единицы до девятнадцати. Эллипс под любым из этих знаков увеличивал его значение в двадцать раз. Примеры цифр Древнего Рима:
1 Буквы пишутся слева направо, начиная с самого большого значения. Например, «XV» – 15, «DLV» – 555, «MCLI» – 1151.
2 Буквы «I», «X», «C», и «M» могут повторяться до трех раз подряд. Например, «II» – 2, «XXX» – 30, «CC» – 200, «MMCCXXX» – 1230.
3 Буквы «V», «L» и «D» не могут повторяться.
4 Цифры 4, 9, 40, 90 и 900 следует писать, комбинируя буквы «IV» – 4, «IX» – 9, «XL» – 40, «XC» – 90, «CD» – 400, «СМ» – 900. Например, 48 это «XLVIII», 449 – «CDXLIX». Значение левой буквы уменьшает значение правой.
5 Горизонтальная линия над буквой увеличивает ее значение на 1000
Из-за использования малого количества знаков для написания цифры приходилось много раз повторять один и тот же знак, образуя длинный ряд символов.В документах ацтекских чиновников встречаются счета, в которых указывались результаты описи и подсчеты податей, получаемых ацтеками от покоренных городов. В этих документах можно увидеть длинные ряды знаков, похожие на настоящие иероглифы. В Китае палочками из слоновой кости или бамбука они обозначали цифры от одного до девяти. Цифры от одного до пяти обозначались количеством палочек, в зависимости от номера. Так, две палочки соответствовали номеру два. А чтобы указать цифры от шести до девяти, одна горизонтальная палочка помещалась в верхней части цифры. Например, 6 напоминала букву «Т».Цифры, или символы наших чисел, имеют арабское происхождение. Арабской культурой, в свою очередь, они были заимствованы в Индии. Промежуток между восьмым и тринадцатым веками стал одним из блестящих периодов в истории науки в мусульманском мире. Мусульмане имели тесные связи как с азиатской, так и с европейской культурами. Они смогли извлечь из них все самое выдающееся. В Индии они заимствовали систему исчисления и некоторые математические знаки.
711 год – можно считать годом открытия индийских цифр на территориях ближнего Востока, в Европу они, конечно же, попали гораздо позже. Почему именно Ближнего востока? Что ж, вполне законный вопрос. Дело в том, что замечательный город Бахда – или как мы привыкли называть его - Багдад в те времена был довольно привлекательным местом для ученых. Там было открыто множество научный и псевдонаучных школ, в которых, тем не менее, шёл обмен полученными знаниями и умениями. В 711 туда попал трактат о звёздах и заодно, о цифрах. Сейчас трудно сказать, были ли прогрессивными взгляды на цифры того индийского учёного представившего миру астрономический доклад, но вот то, что мы при его помощи сейчас обладаем арабскими цифрами поистине не забываемо и заслуживает премногой благодарности. В то время в науке пользовались в основном тремя системами исчисления чисел: римское, греческое и египетско – персидское. В принципе, они были достаточно удобны для ведения небольшого хозяйства скажем одного человека, но записывать при их помощи большие числа было весьма трудно, хотя древнегреческие философы и математики назвали свою систему счёта и записи цифр чуть ли ни самой совершенной в мире. Это по большому счёту, конечно, было не правда.
Способ, придуманный индийцами и принесённый в мир арабами, был более удобный и экономичный, так можно было экономить не только ресурсы для письма (будь-то папирус, бумага или даже что-то другое) но и своё собственное время, которого людям во все времена катастрофический не хватало. Со временем углы сгладились, и цифры приобрели привычный нам вид. Вот уже много столетий весь мир пользуется арабской системой записи чисел. Этими десятью значками можно легко выразить огромные значения. Кстати, слово «цифра» тоже арабское. Арабские математики перевели индийское слово «сунья» по смыслу на свой язык. Вместо «сунья» они стали говорить «сифр» или «цифр», а это уже знакомое нам слово.
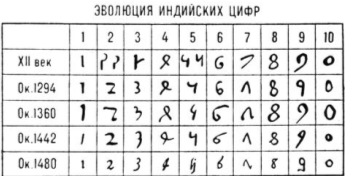
Письменных памятников древнеиндийской цивилизации сохранилось очень немного, но, судя по всему, индийские системы счисления проходили в своем развитии те же этапы, что и во всех прочих цивилизациях. На древних надписях из Мохенджо - Даро вертикальная черточка в записи чисел повторяется до тринадцати раз, а группировка символов напоминает ту, которая знакома нам по египетским иероглифическим надписям. В течение некоторого времени имела хождение система счисления, очень напоминающая аттическую, в которой для обозначения чисел 4, 10, 20 и 100 использовались повторения коллективных символов. Эта система, которая называется кхарошти, постепенно уступила место другой, известной под названием брахми, где буквами алфавита обозначались единицы (начиная с четырех), десятки, сотни и тысячи. Переход от кхарошти к брахми происходил в те годы, когда в Греции, вскоре после вторжения в Индию Александра Македонского, ионическая система счисления вытеснила аттическую. Вполне возможно, что переход от кхарошти к брахми происходил под влиянием греков, но сейчас вряд ли возможно хоть как-то проследить или восстановить этот переход от древних индийских форм к системе, от которой произошли наши системы счисления.
Надписи, найденные в Нана-Гат и Насике, относящиеся к первым векам до нашей эры и первым векам нашей эры, по-видимому, содержат обозначения чисел, которые были прямыми предшественниками тех, которые получили теперь название индо-арабской системы. Первоначально в этой системе не было ни позиционного принципа, ни символа нуля. Оба эти элементы вошли в индийскую систему к 8–9 вв. вместе с обозначениями деванагари (см. таблицу обозначений чиселНапомним, что позиционная система счисления с нулем возникла не в Индии, поскольку за много веков до этого она использовалась в Древнем Вавилоне в связи с шестидесятиричной системой. Поскольку индийские астрономы использовали шестидесятиричные дроби, вполне возможно, что это навело их на мысль перенести позиционный принцип с шестидесятиричных дробей на целые числа, записанные в десятичной системе.
В итоге произошел сдвиг, приведший к современной системе счисления. Не исключена также возможность, что такой переход, по крайней мере отчасти, произошел в Греции, скорее всего в Александрии, и оттуда распространился в Индию. В пользу последнего предположения свидетельствует сходство кружка, обозначающего нуль, с начертанием греческой буквы омикрон.
Вывод
Мы узнали как пишутся цифры Древнего Рима и что они из себя представляют.
Узнали о Древнеиндийских числах, их эволюцию, письмо и виды письма.
3. Китайские цифры
3.1 Цифра Обычный способ Формальный Чтение
0 〇零líng
1 一壹 yī
2 二貳 èr
3 三参 sān
4 四肆 sì
5 五伍 wu
6 六陆 liù
7 七柒 qī
8 八捌 bā
9 九玖 jiu
10 十拾 shí
100 百佰 bai
1000 千仟 qiān
10000 万萬 wàn
100.000.000 亿億 yì
3.2 История
Происхождение китайской системы счисления более древнее и определяется между 1500 и 1200 годами до нашей эры. В конце XIX века крестьяне, возделывающие свои поля, нашли множество черепашьих панцирей и костей животных, исписанных знаками древней китайской системы исчисления. Крестьяне, не знавшие важности этих рисунков, продали эти кости аптекарю, решившему, что они принадлежали дракону и имеют целебные свойства. Много лет спустя в другом регионе Китая появилась новая система исчисления. Потребности торговли, управления и науки потребовали развития нового способа написания цифр. Палочками из слоновой кости или бамбука они обозначали цифры от единицы до девяти. Цифры от единицы до пяти они обозначали количеством палочек в зависимости от номера. Так, две палочки соответствовали номеру 2. Чтобы указать цифры от шести до девяти, одна горизонтальная палочка помещалась в верхней части цифры. Новая система исчисления была отличительной и позиционной: каждая цифра имела определённое значение согласно месту, занимаемому в ряду, выражавшем число.
Уже порядка 4000 тысяч лет китайские цифры являются традиционным способом записи чисел в китайской письменности. Более того, другие языки, такие как японский, корейский, также используют данные китайские символы, для обозначения цифр и чисел. Существует два набора символов для отображения китайских цифр - обычная запись для повседневного использования и формальная запись, используемая в финансовом контексте, например, для заполнения чеков. Более сложные по форме символы, используемые в формальной записи, очень сильно затрудняют подделку финансовых документов.
В России и в других европейских странах с той же целью используется сумма прописью. Числа в этой китайской системе, так же как и у нас, в арабских числах, записывались слева направо, от больших к меньшим. Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда - кружок, который является аналогом нашего нуль.
Вывод
Мы узнали о Китайских числах: как они пишутся, откуда и когда произошли и что они из себя представляют.
4. Цифры деванагари
Деванагари — разновидность индийского письма, произошедшая от древнеиндийского письма брахми. Сложилась между VIII и XII веками. Применяется в санскрите, хинди, маратхи, синдхи, бихари, бхили, марвари, конкани, бходжпури, непали, неварском языке, а также иногда в кашмири и романи. Характерной особенностью письма деванагари является верхняя (базовая) горизонтальная черта, к которой прикреплены «свисающие» вниз буквы. Дева-Нага-Ри" - Божественных Нагов письмо (или речь).
Принципы построения графики
В деванагари каждый знак для согласного по умолчанию содержит и обозначение гласного звука (a). Чтобы обозначить согласный без гласного, нужно добавить специальный подстрочный значок — халант (вирама). Для обозначения других гласных, как и в семитских письменных системах, используются диакритики. Специальные обозначения используются для гласных в начале слова. Согласные могут образовывать сочетания, в которых соответствующие гласные пропускаются. Сочетания согласных обычно записываются как слитные, или составные знаки (лигатуры).
"Деванагари", "Дева" - божественный, (однокоренные слова - "дивный", "удивительный")
"Нага" - Наги (мифический народ людей-змей) обитавший, согласно преданиям, в Индии в глубокой древности. Наги могли быть богами, полубогами, или приближенными богов.
"Ри" - (однокоренное слово речь) речь письмо, закон, порядок, ритуал.
Вывод
Мы узнали многое о числах Деванагари: как они пишутся и их расшифровка
5. Современные цифры
Как бы велико ни было число, его можно записать с помощью всего лишь десяти числовых знаков, цифр: 1, 2, 3, 4, 5, б, 7, 8, 9, 0. Цифр, как и правил арифметики, никто сразу не выдумал, не изобрел. Современные цифры были выработаны на протяжении многих веков. Совершенствование начертания цифр шло параллельно с развитием письменности. Вначале букв не было. Мысли и слова выражались, при помощи рисунков на скалах, на стенах пещер, на камнях. Для запоминания чисел люди пользовались зарубками на деревьях и на палках и узлами на веревках. Далее естественно стали обозначать число один — одной черточкой, два — двумя, три — тремя черточками и т.д. Следы таких цифр имеются, например, в римской системе: I, II, III. Но с развитием производства и культуры, когда появилась нужда записывать большие числа, стало неудобно пользоваться черточками. Тогда стали вводить особые знаки для отдельных чисел. Каждое число, как и каждое слово, обозначалось особым значком, иероглифом.
В Древнем Египте около 4000 лет назад имелись другие значки и иероглифы для обозначения чисел. Единица изображена колом, десяток — как бы парой рук, сотня — свернутым пальмовым листом, тысяча — цветком лотоса, символом обилия, сто тысяч — лягушкой, так как лягушек было очень много во время разлива Нила. В дальнейшем появляются особые обозначения отдельных звуков, то есть буквы. Было время, когда буквами пользовались и в качестве цифр. Так поступали древние греки, славяне и другие народы. Чтобы отличить буквы от чисел, славяне ставили над буквами, изображающими числа, особый знак, названный «титло». Эта нумерация, называемая алфавитной, также оказалась со временем неудобной.
Потребности практики, развитие производства и торговли способствовали созданию более удобных, современных цифр и образованию современной письменной нумерации. Всем известны римские цифры. Некоторые из этих семи знаков служили и буквами. Римляне обозначали буквой М тысячу. Вот, например, как записывалось число 38 784: XXXVIIImDCCLXXXIV.
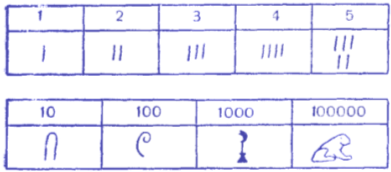
Неудобна была римская нумерация по сравнению с нашей десятичной: записи длинные, умножение и деление в письменном виде производить невозможно. Все действия надо производить в уме. Даже чтобы прочитать число, нужно устно складывать или вычитать потому, что каждая из семи римских цифр означает всюду, где бы она ни стояла, одно и то же число. Например, V означает пять единиц как в числе VI, так и в числе IV. В современной же письменной нумерации не только вид, начертание цифры, но и ее место, ее положение, ее позиция среди других цифр имеет значение. Например, в числе 15 цифра 5 означает 5 единиц, а в числе 53 та же цифра 5 означает пять десятков, т. е. пятьдесят единиц. Именно поэтому наша нумерация называется позиционной. Она, как и современные цифры, возникла примерно 1500 лет назад в Индии. Это не значит, что индийские цифры имели с самого начала современный вид.
В течение многих столетий, переходя от народа к народу, старинные индийские цифры много раз изменялись, пока приняли современную форму. Арабы заимствовали у индийцев цифры и позиционную десятичную систему, которую европейцы в свою очередь заимствовали у арабов. Поэтому наши цифры, в отличие от римских, стали называть арабскими. Правильнее было бы их называть индийскими. Эти цифры употребляются в нашей стране начиная с XVII в. Римские же цифры применяются лишь в исключительных случая.
Вывод
Мы узнали о современных цифрах: их историю, написание и обозначении
Заключение
Мы узнали много новых и интересных фактов о цифрах разных народов, проследили их развитие от Древности до наших дней. Поняли, почему неудобна система счисления Древнего Рима. Узнали как, откуда и когда европейцы узнали об арабских цифрах, и почему в дальнейшем они стали их использовать в повседневной жизни. Узнали о написании, истории и развитии арабских цифр.
Литература
1. Информация предоставлена с сайта :http://ru.wikipedia.org/wiki/
|