КОНТРОЛЬНАЯ РАБОТА
«Расчет балки таврового сечения по двум группам предельных состояний»
1. Рассчитать арматуру тавровой балки;
2. Рассчитать максимальный прогиб.
| Номер варианта
|
Номер схемы
|
Нагрузка
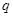 ,
,
кН/м
|
Нагрузка
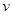 ,
,
кН/м
|
Длина
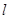 ,
,
м
|
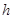 ,
,
м
|
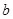 ,
,
м
|
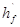 ,
,
м
|
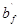 ,
,
м
|
| 12 |
2 |
14,4 |
8 |
6,0 |
0,5 |
0,15 |
0,15 |
0,5 |
схема 2 – шарнирно опертая балка нагружена сосредоточенной силой 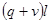 в середине пролета. в середине пролета.
Для нахождения значений поперечных сил и изгибающих моментов, действующих в сечении балки, составляем уравнения равновесия сил и моментов:
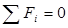 ; ; 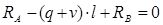
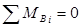 ; ; 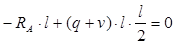
Тогда реакции опор равны: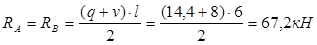
Для построенния эпюры изгибающих моментов рассмотрим два участка:
I:
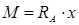 ; – эпюра имеет очертание прямой ; – эпюра имеет очертание прямой
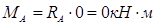
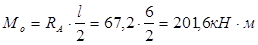 ; ;
II:
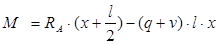 - эпюра имеет очертание прямой - эпюра имеет очертание прямой
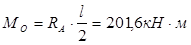
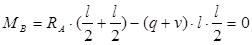
Опасное сечение в середине пролёта, максимальное значение изгибающего момента

Строим эпюры Рис. 1
.
Выбираем бетон класса В20 (Rb
=10,5 МПа при gb
2
=
0,9); арматуру класса A-III (Rs
=
365 МПа).
h
0
=
500 – 40 =
460 мм. Расчет производим согласно п. 3.22 [2] в предположении, что сжатая арматура по расчету не требуется.
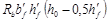 = 10,5 · 500 · 150 (460 – 0,5 · 150) =
303,2 · 106
Н ·мм =
303,2 кН · м > М
=
201,6 кН ·м,
т.е. граница сжатой зоны проходит в полке = 10,5 · 500 · 150 (460 – 0,5 · 150) =
303,2 · 106
Н ·мм =
303,2 кН · м > М
=
201,6 кН ·м,
т.е. граница сжатой зоны проходит в полке
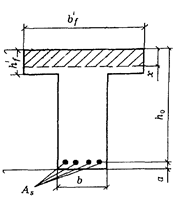
Рис. 2 Сечение балки. Положение границы сжатой зоны
Расчет производим как для прямоугольного сечения шириной b =
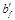 =
500 мм согласно п. 3.18 [2].
=
500 мм согласно п. 3.18 [2].
Вычислим значение a
m
:
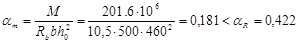
т.е. сжатая арматура действительно не требуется.
Площадь сечения растянутой арматуры вычислим по формуле (23) [2]. Для этого по табл. 20 [2] при am
=
0,181 находим z методом интерполяции:
| z |
am
|
| 0,900 |
0,180 |
| 0,895 |
0,188 |
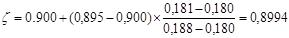
тогда
 мм2
=13,356 см2
. мм2
=13,356 см2
.
Принимаем 2 Æ 20 (As
=
6,28 см2
=628 мм2
) + 2
Æ 22 (As
=
7,6 см2
=760 мм2
).
As
=
13,88 см2
= 1388 мм2
Расчет железобетонных элементов на действие поперечной,
силы для обеспечения прочности по наклонной полосе между наклонными трещинами должен производиться из условия
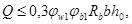
где Q
–
поперечная сила в нормальном сечении, принимаемом на расстоянии от опоры не менее h
0,
Q
=67,2 кН
;
j
w
1
– коэффициент, учитывающий влияние хомутов, нормальных к оси элемента, и определяемый по формуле
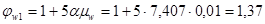
j
w
должен быть не более 1,3;
поэтому принимаем j
w
1
=1,3
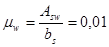
j
b
1
– коэффициент, определяемый по формуле
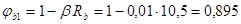
здесь b
–
коэффициент, принимаемый равным для тяжелого бетона – 0,
Rb
= 10,5 МПа для выбранного бетона.
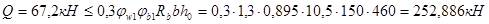 - условие выполняется. - условие выполняется.
Рассматриваем участок балки на длине 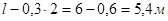 (без участков у опор длиной 0,3 м). (без участков у опор длиной 0,3 м).
Из условия сварки принимаем диаметр хомутов 6 мм арматуры A-III.
Первоначально задаёмся шагом хомутов в приопорном участке балки 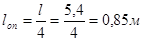 : : 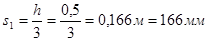 , принимаем , принимаем 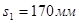
Шаг хомутов в пролёте балки 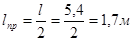 : : 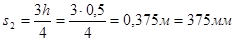
При этом шаг должен быть не более 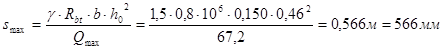
Уточняем шаг хомутов в пролёте 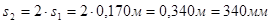
Количество хомутов в приопорных участках 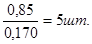 , в пролёте , в пролёте 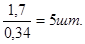
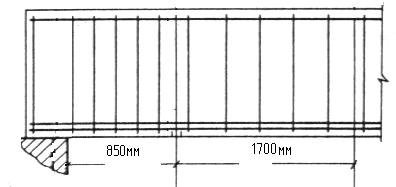
Рис. 2 Продольное сечение балки. Хомуты поперечной арматуры.
Спецификация арматуры
| Обозначение арматуры |
Длина, м |
Кол-во хомутов, шт. |
Масса
1 м,
кг
|
Масса общая,
кг
|
Масса всех элементов каркаса, кг |
| A-III Æ 20 |
5,4 |
2 |
2,466 |
26,633 |
| A-III Æ 22 |
5,4 |
2 |
2,984 |
26,633 |
| A-III Æ6 |
15 |
0,222 |
1. СНиП 52–01–2003. Бетонные и железобетонные конструкции. Основные положения. М., 2004. С. 24.
2. Пособие по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры (к СНиП 2.03.01–84). М.: ЦНИИПромзданий Госстроя СССР, НИИЖБ Госстроя СССР, 1989. 192 с.
3. СНиП 2.01.07–85. Нагрузки и воздействия. М., 1988. 34 с.
|